ﺟﺒﺮ ﺑﻮﻝ Boolean Algebra ﺟﺒﺮ

ﺟﺒﺮ ﺑﻮﻝ Boolean Algebra

ﺟﺒﺮ ﺑﻮﻝ : • ﻗﻮﺕ ﺍﺻﻠﻲ ﺳﻴﺴﺘﻢ ﻫﺎﻱ ﺩﻳﺠﻴﺘﺎﻝ ﺟﺎﻣﻌﻴﺖ ﻭ ﻗﺪﺭﺕ ﻓﺮﻣﻮﻻﺳﻴﻮﻥ ﺭﻳﺎﺿﻲ ﺟﺒﺮ ﺑﻮﻝ Ø : • ﻣﺜﺎﻝ IF the garage door is open AND the car is running THEN the car can be backed out of the garage : ﻫﺮ ﺩﻭﺷﺮﻁ ﻭ the door must be open The car is running. ﺑﺎﺷﻨﺪ ﺗﺎ ﺑﺘﻮﺍﻥﻣﺎﺷﻴﻦ ﺭﺍ ﺍﺯ گﺎﺭﺍژ ﺑﻴﺮﻭﻥ آﻮﺭﺩ true ﺑﺎﻳﺪ 2

Digital Systems: Boolean Algebra and Logical Operations • In Boolean algebra: Ø Values: 0, 1 Ø 0: if a logic statement is false, Ø 1: if a logic statement is true. • Operations: AND, OR, NOT 3

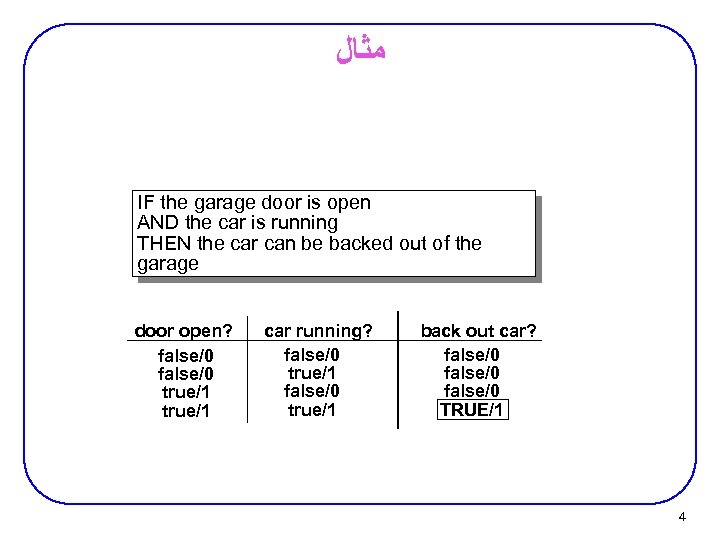
ﻣﺜﺎﻝ IF the garage door is open AND the car is running THEN the car can be backed out of the garage door open? false/0 true/1 car running? false/0 true/1 back out car? false/0 TRUE/1 4

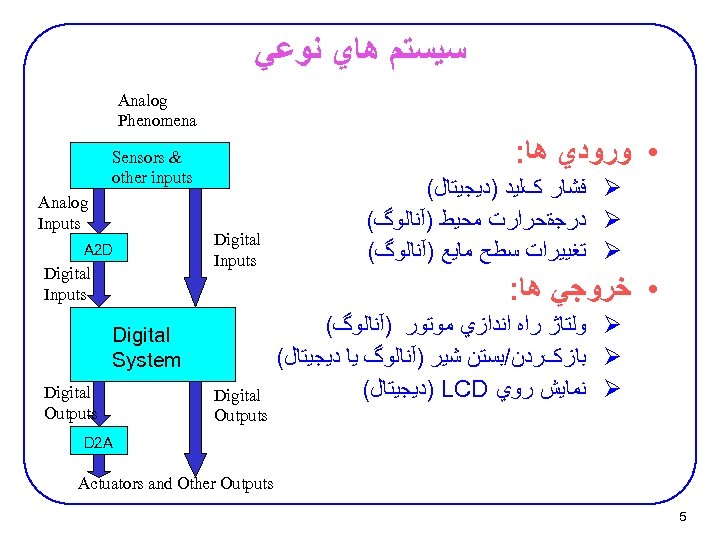
ﺳﻴﺴﺘﻢ ﻫﺎﻱ ﻧﻮﻋﻲ Analog Phenomena : • ﻭﺭﻭﺩﻱ ﻫﺎ Sensors & other inputs Analog Inputs A 2 D Digital Inputs ( ﻓﺸﺎﺭ کﻠﻴﺪ )ﺩﻳﺠﻴﺘﺎﻝ Ø ( ﺩﺭﺟةﺤﺮﺍﺭﺕ ﻣﺤﻴﻂ )آﻨﺎﻟﻮگ Ø ( ﺗﻐﻴﻴﺮﺍﺕ ﺳﻄﺢ ﻣﺎﻳﻊ )آﻨﺎﻟﻮگ Ø : • ﺧﺮﻭﺟﻲ ﻫﺎ Digital System Digital Outputs ( ﻭﻟﺘﺎژ ﺭﺍﻩ ﺍﻧﺪﺍﺯﻱ ﻣﻮﺗﻮﺭ )آﻨﺎﻟﻮگ Ø ( ﺑﺎﺯکﺮﺩﻥ/ﺑﺴﺘﻦ ﺷﻴﺮ )آﻨﺎﻟﻮگ ﻳﺎ ﺩﻳﺠﻴﺘﺎﻝ Ø ( )ﺩﻳﺠﻴﺘﺎﻝ LCD ﻧﻤﺎﻳﺶ ﺭﻭﻱ Ø D 2 A Actuators and Other Outputs 5

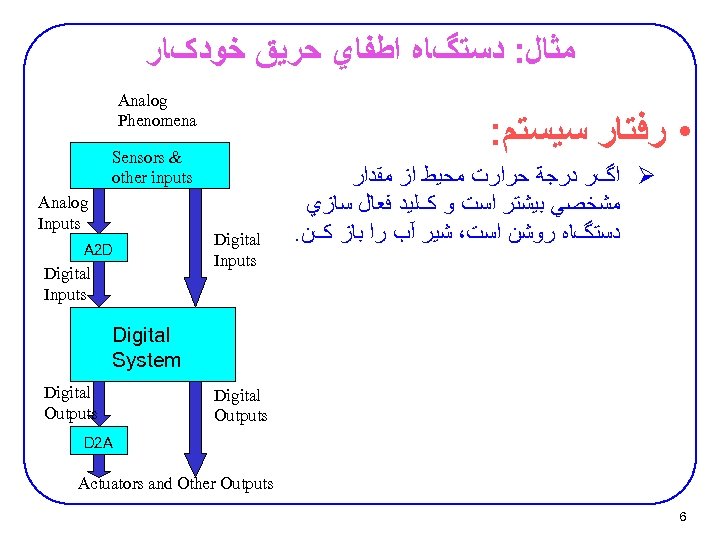
ﻣﺜﺎﻝ: ﺩﺳﺘگﺎﻩ ﺍﻃﻔﺎﻱ ﺣﺮﻳﻖ ﺧﻮﺩکﺎﺭ Analog Phenomena : • ﺭﻓﺘﺎﺭ ﺳﻴﺴﺘﻢ Sensors & other inputs Analog Inputs A 2 D Digital Inputs ﺍگﺮ ﺩﺭﺟﺔ ﺣﺮﺍﺭﺕ ﻣﺤﻴﻂ ﺍﺯ ﻣﻘﺪﺍﺭ Ø ﻣﺸﺨﺼﻲ ﺑﻴﺸﺘﺮ ﺍﺳﺖ ﻭ کﻠﻴﺪ ﻓﻌﺎﻝ ﺳﺎﺯﻱ . ﺩﺳﺘگﺎﻩ ﺭﻭﺷﻦ ﺍﺳﺖ، ﺷﻴﺮ آﺐ ﺭﺍ ﺑﺎﺯ کﻦ Digital System Digital Outputs D 2 A Actuators and Other Outputs 6

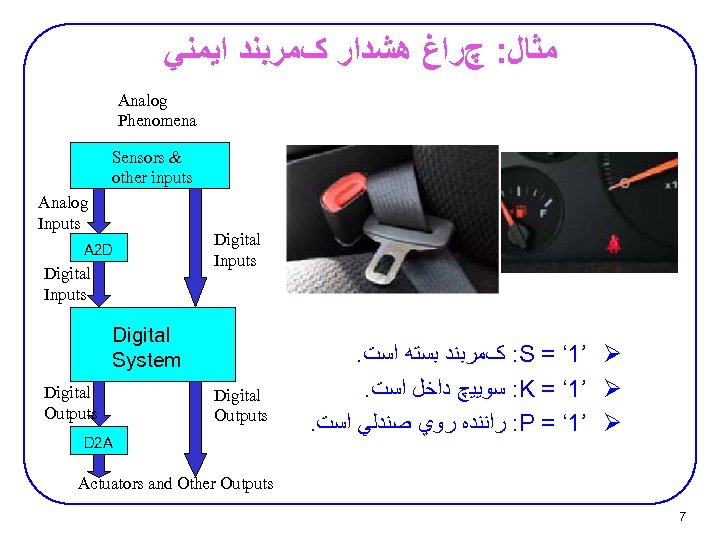
ﻣﺜﺎﻝ: چﺮﺍﻍ ﻫﺸﺪﺍﺭ کﻤﺮﺑﻨﺪ ﺍﻳﻤﻨﻲ Analog Phenomena Sensors & other inputs Analog Inputs A 2 D Digital Inputs Digital System Digital Outputs D 2 A . : کﻤﺮﺑﻨﺪ ﺑﺴﺘﻪ ﺍﺳﺖ S = ‘ 1’ Ø. : ﺳﻮﻳﻴچ ﺩﺍﺧﻞ ﺍﺳﺖ K = ‘ 1’ Ø. : ﺭﺍﻧﻨﺪﻩ ﺭﻭﻱ ﺻﻨﺪﻟﻲ ﺍﺳﺖ P = ‘ 1’ Ø Actuators and Other Outputs 7

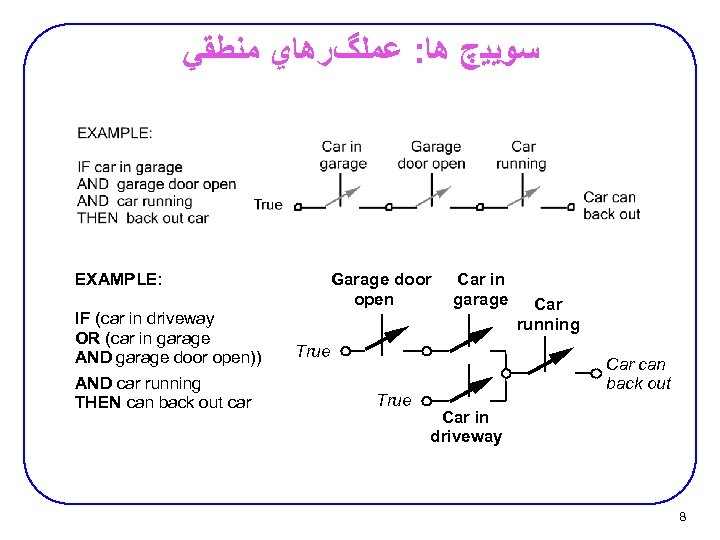
ﺳﻮﻳﻴچ ﻫﺎ: ﻋﻤﻠگﺮﻫﺎﻱ ﻣﻨﻄﻘﻲ EXAMPLE: IF (car in driveway OR (car in garage AND garage door open)) AND car running THEN can back out car Garage door open Car in garage True Car running Car can back out Car in driveway 8

Binary Logic ØDeals with binary variables that take 2 discrete values (0 and 1), and with logic operations ØBasic logic operations: − AND, OR, NOT ØBinary/logic variables are typically represented as letters: A, B, C, …, X, Y, Z 9

Binary Logic Function F(vars) = expression n. Operators set of binary variables Example: n. Variables ( +, • , ‘ ) n. Constants ( 0, 1 ) n. Groupings (parenthesis) F(a, b) = a’ • b + b’ G(x, y, z) = x • (y+z’) 10

Basic Logic Operators ØAND (also • , ) ØOR (also +, ) ØNOT (also ’, ) Binary Unary ØF(a, b) = a • b, reads F is 1 if and only if a=b=1 ØG(a, b) = a+b, reads G is 1 if either a=1 or both ØH(a) = a’, reads H is 1 if a=0 11

Basic Logic Operators (cont. ) • 1 -bit logic AND resembles binary multiplication: 0 • 0 = 0, 1 • 0 = 0, 0 • 1 = 0, 1 • 1 =1 • 1 -bit logic OR resembles binary addition, except for one operation: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 1 (≠ 102) 12

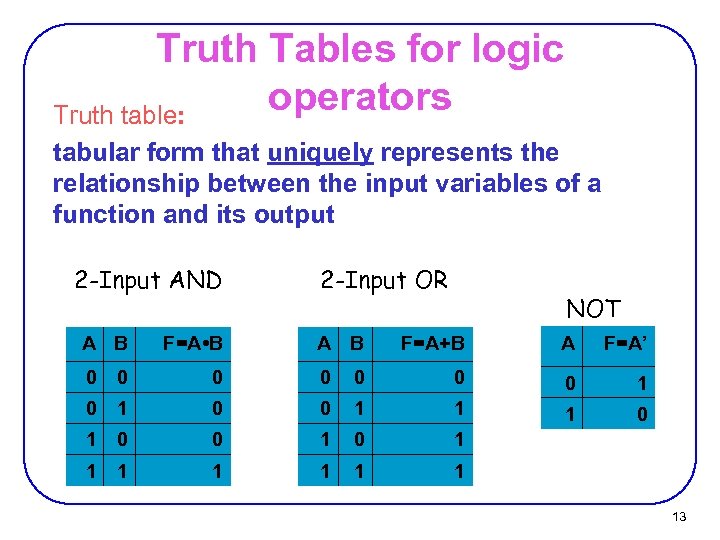
Truth Tables for logic operators Truth table: tabular form that uniquely represents the relationship between the input variables of a function and its output 2 -Input AND A B F=A • B 2 -Input OR A B NOT F=A+B A F=A’ 0 0 0 0 1 1 1 0 0 1 1 1 1 13

Truth Tables (cont. ) • Q: ØLet a function F() depend on n variables. How many rows are there in the truth table of F() ? • A: n n Ø 2 rows, since there are 2 possible binary patterns/combinations for the n variables 14

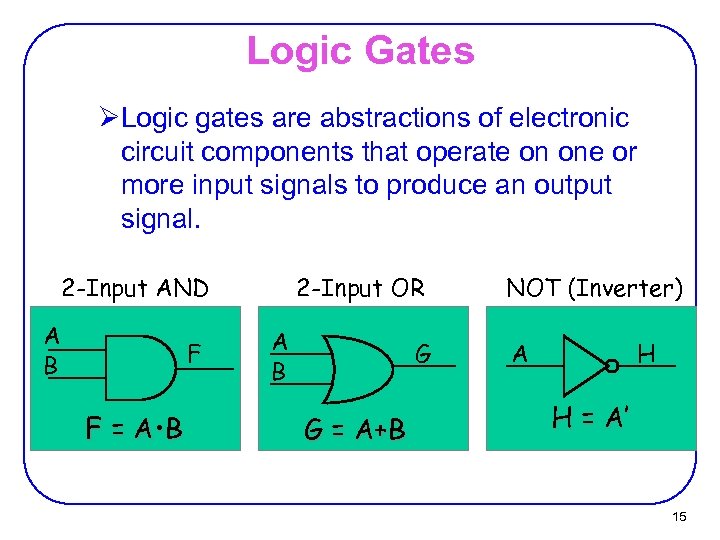
Logic Gates ØLogic gates are abstractions of electronic circuit components that operate on one or more input signals to produce an output signal. 2 -Input AND A B F F = A • B 2 -Input OR A B G G = A+B NOT (Inverter) A H H = A’ 15

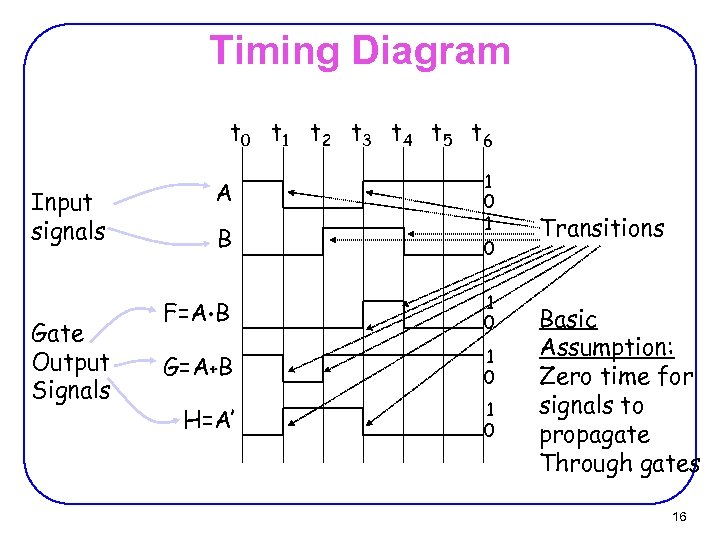
Timing Diagram t 0 t 1 t 2 t 3 t 4 t 5 t 6 Input signals Gate Output Signals B 1 0 F=A • B 1 0 G=A+B 1 0 H=A’ 1 0 A Transitions Basic Assumption: Zero time for signals to propagate Through gates 16

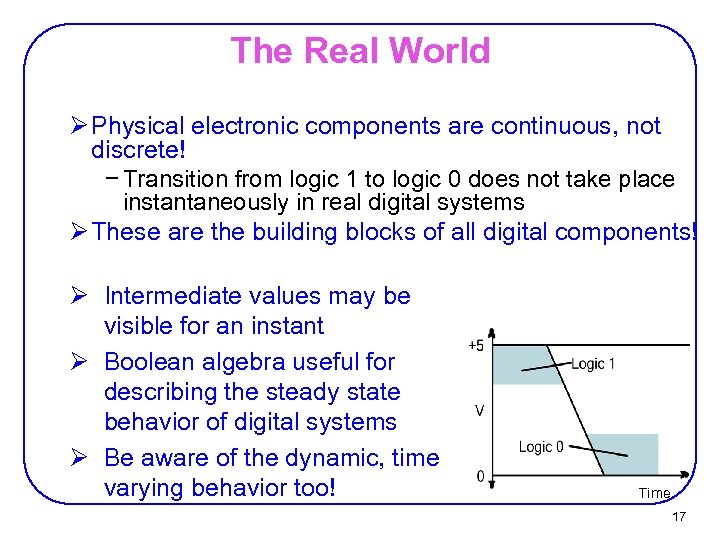
The Real World Ø Physical electronic components are continuous, not discrete! − Transition from logic 1 to logic 0 does not take place instantaneously in real digital systems Ø These are the building blocks of all digital components! Ø Intermediate values may be visible for an instant Ø Boolean algebra useful for describing the steady state behavior of digital systems Ø Be aware of the dynamic, time varying behavior too! Time 17

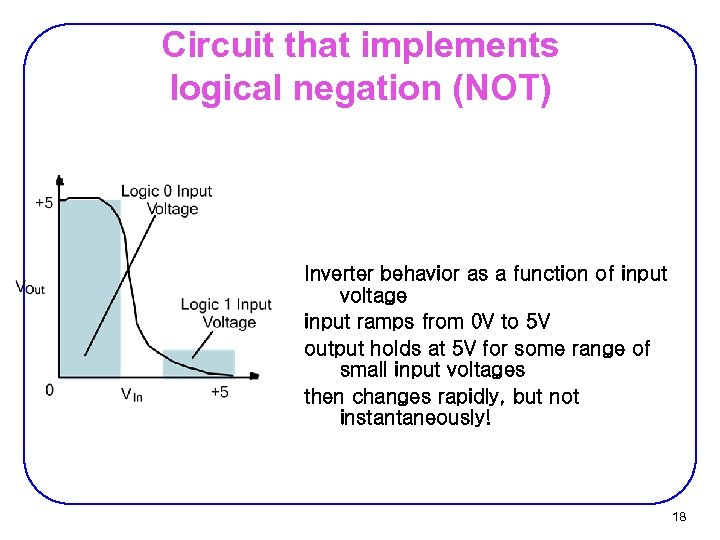
Circuit that implements logical negation (NOT) Inverter behavior as a function of input voltage input ramps from 0 V to 5 V output holds at 5 V for some range of small input voltages then changes rapidly, but not instantaneously! 18

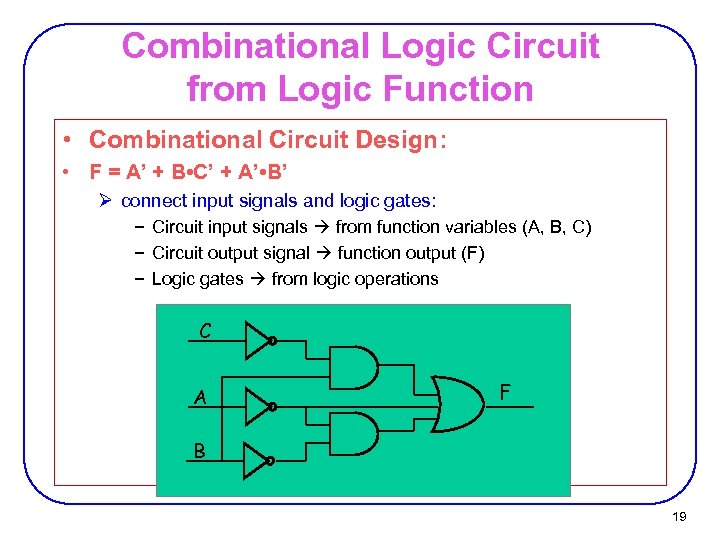
Combinational Logic Circuit from Logic Function • Combinational Circuit Design: • F = A’ + B • C’ + A’ • B’ Ø connect input signals and logic gates: − Circuit input signals from function variables (A, B, C) − Circuit output signal function output (F) − Logic gates from logic operations C A F B 19

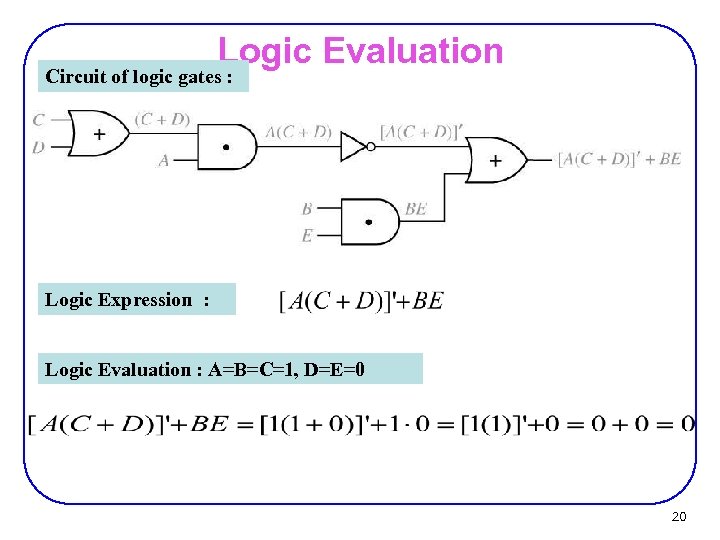
Logic Evaluation Circuit of logic gates : Logic Expression : Logic Evaluation : A=B=C=1, D=E=0 20

Combinational Logic Optimization Ø In order to design a cost-effective and efficient circuit, we must minimize − the circuit’s size − area − propagation delay − time required for an input signal change to be observed at the output line Ø Observe the truth table of F=A’ + B • C’ + A’ • B’ and G=A’ + B • C’ are identical same function A B C 0 0 0 1 0 F G 1 1 1 0 1 1 1 0 0 1 0 Ø Use G to implement the logic circuit − less components 21

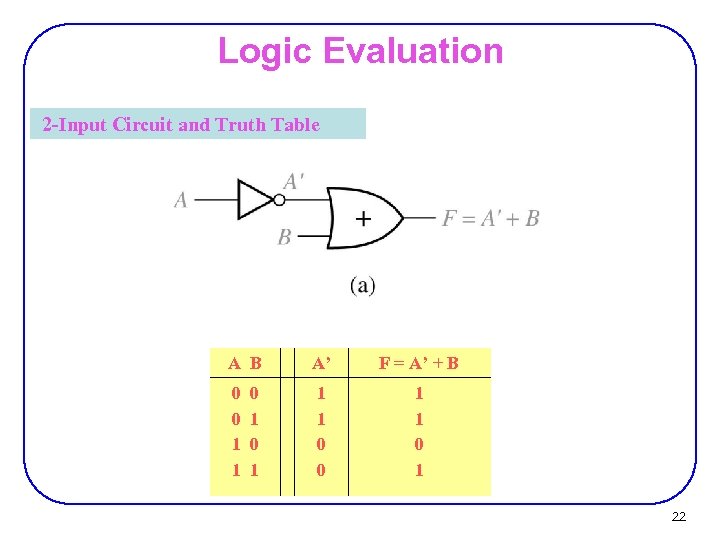
Logic Evaluation 2 -Input Circuit and Truth Table A B A’ F = A’ + B 0 0 1 1 0 1 0 1 22

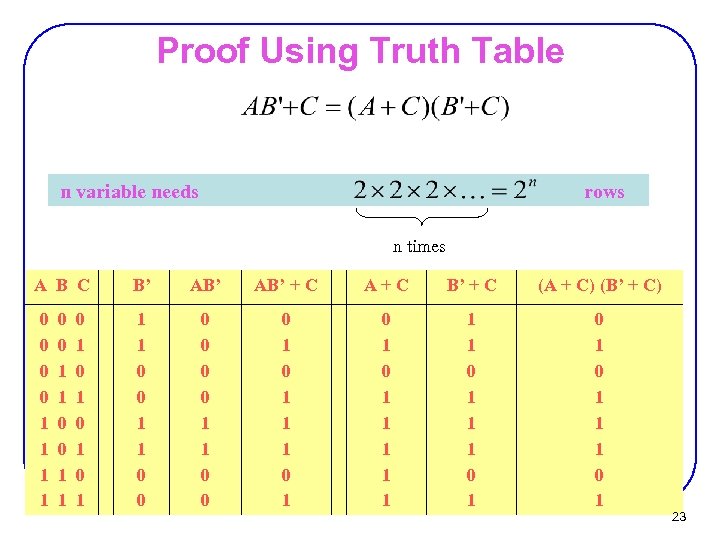
Proof Using Truth Table n variable needs rows n times A B C 0 0 1 1 0 1 0 1 B’ AB’ + C A+C B’ + C (A + C) (B’ + C) 1 1 0 0 0 0 1 1 1 0 1 0 1 1 1 0 1 0 1 1 1 0 1 23

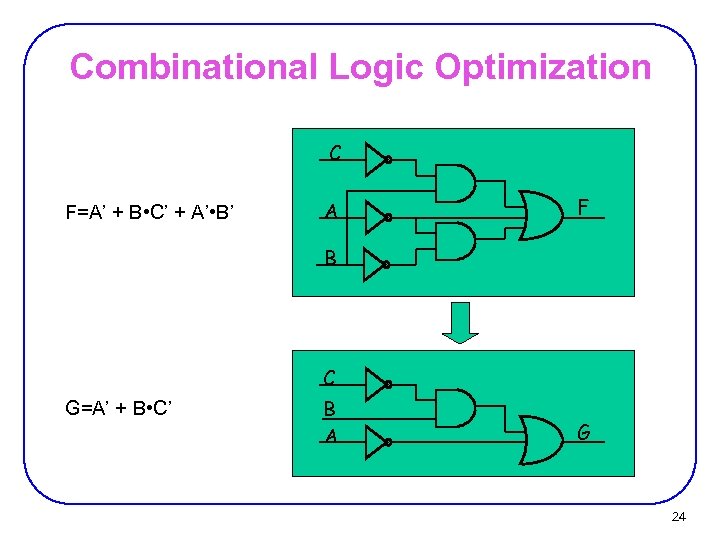
Combinational Logic Optimization C F=A’ + B • C’ + A’ • B’ A F B C G=A’ + B • C’ B A G 24

Boolean Algebra ØVERY nice machinery used to manipulate (simplify) Boolean functions ØGeorge Boole (1815 -1864): “An investigation of the laws of thought” ØTerminology: − Literal: A variable or its complement A, B’, x’ − Product term: literals connected by • X. Y A. B’. C. D, − Sum term: literals connected by + A+B’ A’+B’+C 25

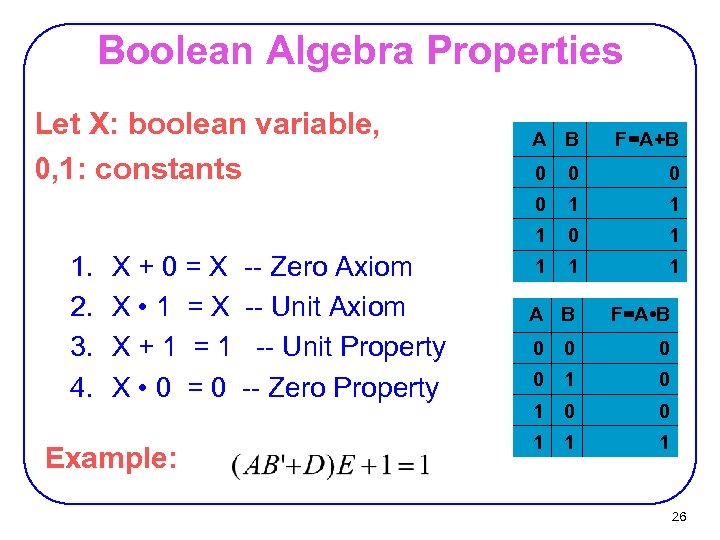
Boolean Algebra Properties Let X: boolean variable, 0, 1: constants A B F=A+B Example: -- Zero Axiom -- Unit Property -- Zero Property 0 1 1 1 X+0=X X • 1 =X X+1 =1 X • 0 =0 0 0 1. 2. 3. 4. 0 0 1 1 A B F=A • B 0 0 1 1 1 26

Boolean Algebra Properties (cont. ) Let X: boolean variable, 0, 1: constants 1. 2. 3. 4. 5. Example: X+X=X X • X =X X + X’ = 1 X • X’ = 0 (X’)’ = X -- Idempotent -- Complement -- Involution A B F=A+B 0 0 1 1 1 0 1 1 A B F=A • B 0 0 1 1 1 27

The Duality Principle Ø The dual of an expression is obtained by exchanging ( • and +), and (1 and 0) in it, − provided that the precedence of operations is not changed. Ø Do not exchange x with x’ Ø Example: − Find H(x, y, z), the dual of F(x, y, z) = x’yz’ + x’y’z − H = (x’+y+z’) (x’+y’+ z) Ø Dual does not always equal the original expression • If a Boolean equation/equality is valid, its dual is also valid 28

The Duality Principle (cont. ) With respect to duality, Identities 1 – 8 have the following relationship: 1. X+0=X 2. X • 1 =X (dual of 1) 3. X+1 =1 4. X • 0 =0 (dual of 3) 5. X+X=X 6. X • X = X (dual of 5) 7. X + X’ = 1 8. X • X’ = 0 (dual of 8) 29

More Boolean Algebra Properties Let X, Y, and Z: boolean variables 10. 12. 14. X+Y=Y+X 11. X • Y = Y • X -- Commutative X + (Y+Z) = (X+Y) + Z 13. X • (Y • Z) = (X • Y) • Z -- Associative X • (Y+Z) = X • Y + X • Z 15. X+(Y • Z) = (X+Y) • (X+Z) -- Distributive 16. (X + Y)’ = X’ • Y’ 17. (X • Y)’ = X’ + Y’ -- De. Morgan’s In general, ( X 1 + X 2 + … + Xn )’ = X 1’ • X 2’ • … • Xn’ ( X 1 • X 2 • … • Xn )’ = X 1’ + X 2’ + … + Xn’ 30

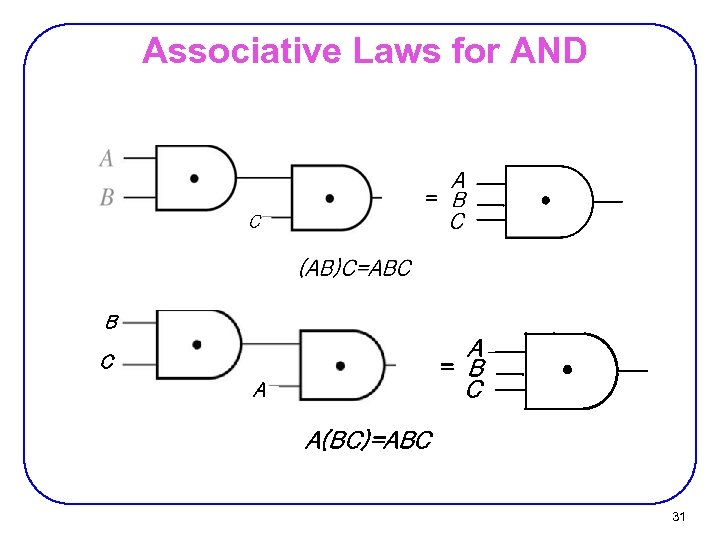
Associative Laws for AND B A = B C C A A(BC)=ABC 31

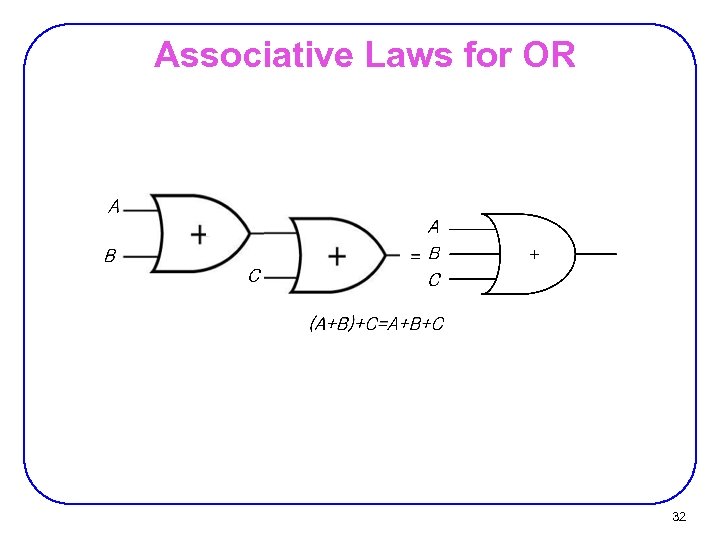
Associative Laws for OR 32

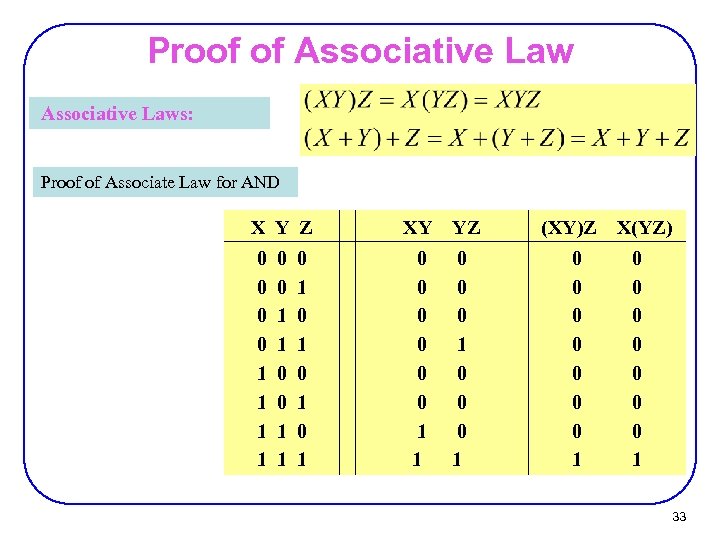
Proof of Associative Laws: Proof of Associate Law for AND X Y Z 0 0 1 1 0 1 0 1 XY 0 0 0 1 1 YZ 0 0 0 1 (XY)Z 0 0 0 0 1 X(YZ) 0 0 0 0 1 33

Distributive Laws: Valid only for Boolean algebra not for ordinary algebra Proof of the second law: (A+B). C = A. C + B. C C 34

Absorption Property (Covering) 1. x + x • y = x 2. x • (x+y) = x (dual) • Proof: x + x • y = x • 1 + x • y = x • (1+y) = x • 1 =x QED (2 true by duality) 35

Absorption Property (Covering) 1. x + x’ • y = x + y 2. x • (x’+y) = x y (dual) • Proof of 2: x • (x’+ y) = x • x’ + x • y = 0 + (x • y) = x • y QED (1 true by duality) 36

De. Morgan’s Laws Proof X Y 0 0 1 1 0 1 X’ Y’ 1 1 0 0 1 0 X+Y ( X + Y )’ X’ Y’ XY ( XY )’ X’ + Y’ 0 1 1 0 0 0 1 1 0 1 1 1 0 De. Morgan’s Laws for n variables Example 37

Consensus Theorem 1. xy + x’z + yz = xy + x’z 2. (x+y) • (x’+z) • (y+z) = (x+y) • (x’+z) -(dual) Proof: xy + x’z + yz = xy + x’z + (x+x’)yz = xy + x’z + xyz + x’yz = (xy + xyz) + (x’z + x’zy) = xy + x’z QED (2 true by duality). 38

Consensus Theorem Example: 39

Consensus Theorem Example: 40

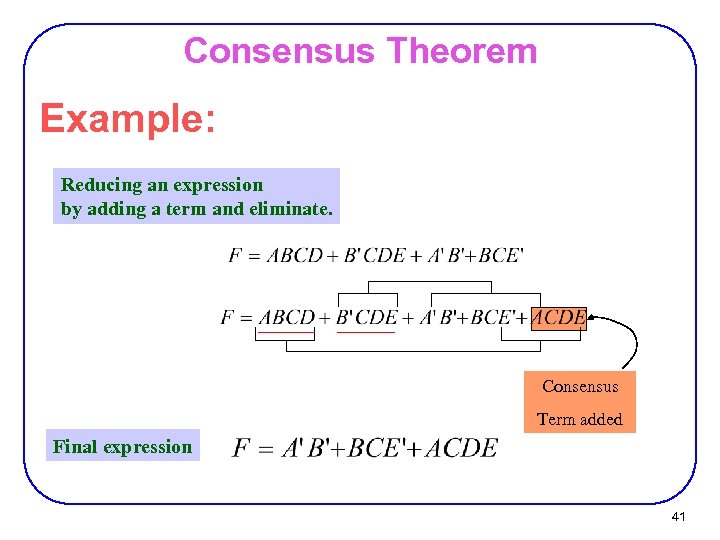
Consensus Theorem Example: Reducing an expression by adding a term and eliminate. Consensus Term added Final expression 41

Algebraic Manipulation ×Boolean algebra is a useful tool for simplifying digital circuits. ×Why do simplification? − Simpler can mean cheaper, smaller, faster • reduce number of literals (gate inputs) • reduce number of gates • reduce number of levels of gates • Fan-ins (number of gate inputs) are limited in some technologies • Fewer levels of gates implies reduced signal propagation delays • Number of gates (or gate packages) influences manufacturing costs 42

Algebraic Simplification 1. Combining terms Example: 2. Adding terms using Example: 3. Eliminating terms Example: 43

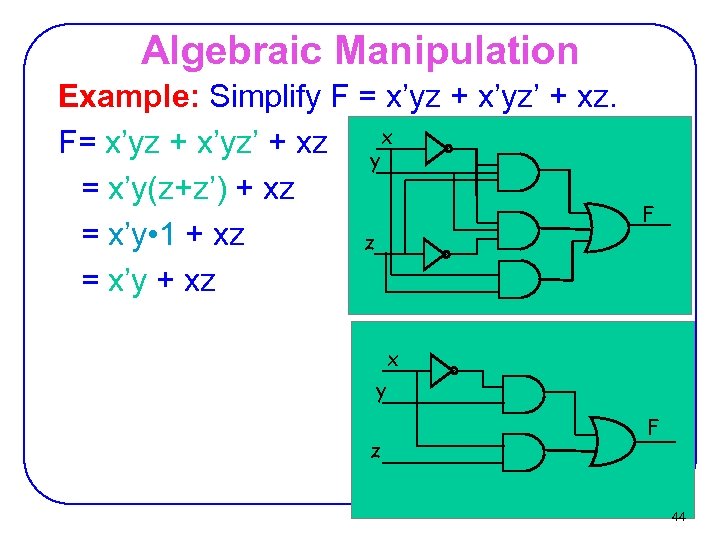
Algebraic Manipulation Example: Simplify F = x’yz + x’yz’ + xz. F= x’yz + x’yz’ + xz y x = x’y(z+z’) + xz = x’y • 1 + xz z = x’y + xz F x y z F 44

Algebraic Manipulation (cont. ) Example: Prove x’y’z’ + x’yz’ + xyz’ = x’z’ + yz’ ×Proof: x’y’z’+ x’yz’+ xyz’ = x’y’z’ + x’yz’ + xyz’ = x’z’(y’+y) + yz’(x’+x) = x’z’ • 1 + yz’ • 1 = x’z’ + yz’ QED. 45

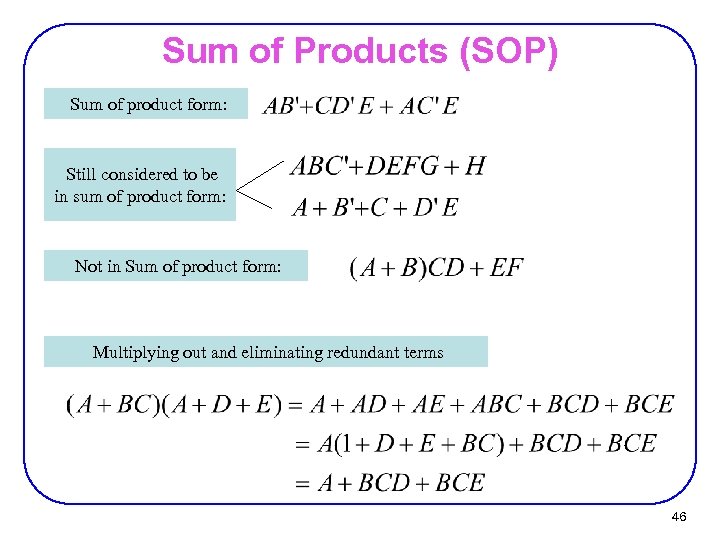
Sum of Products (SOP) Sum of product form: Still considered to be in sum of product form: Not in Sum of product form: Multiplying out and eliminating redundant terms 46

Product of Sums (POS) Product of sum form: Still considered to be in product of sum form: 47

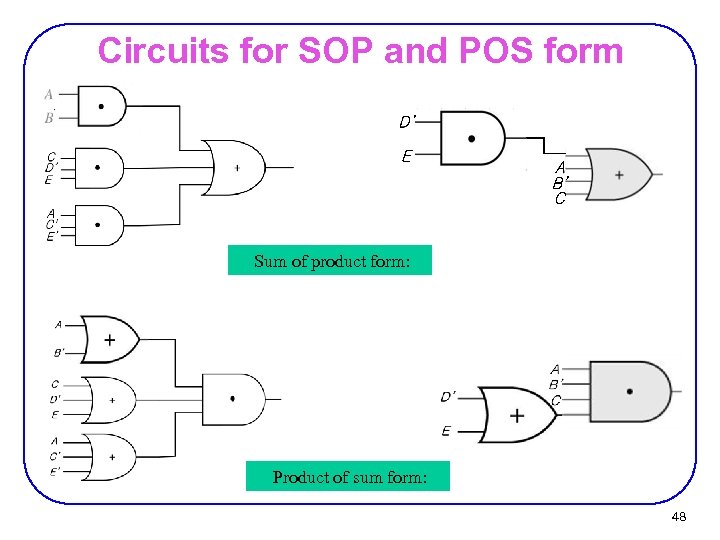
Circuits for SOP and POS form Sum of product form: Product of sum form: 48

Multiplying Out and Factoring To obtain a sum-of-product form Multiplying out using distributive laws Theorem for multiplying out: 68 7 ( X + Y )( X ' + Z ) = XZ + X ' Y 14 244 4 3 (3 -3) If X = 0, (3 - 3) reduces to Y(1 + Z) = 0 + 1*Y or Y = Y. If X = 1, (3 - 3) reduces to (1 + Y)Z = Z + 0 *Y or Z = Z. because the equation is valid for both X = 0 and X = 1, it is always valid. Example: The use of Theorem 3 -3 for factoring: 68 7 A 4+ 4 B 'C 1 2 A 3 = ( A + C )( A'+ B) 49

Multiplying out Theorem for multiplying out: (Q + AB' )(C ' D + Q' ) = QC ' D + Q' AB' Multiplying out using distributive laws Redundant terms multiplying out: (a) distributive laws (b) theorem(3 -3) ( A + B + C ' )( A + B + D)( A + B + E )( A + D' +E )( A' +C ) = ( A + B + C ' D)( A + B + E )[ AC + A' ( D' +E )] = ( A + B + C ' DE )( AC + A' D' +A' E ) = AC + ABC + A' BD' +A' BE + A' C ' DE What theorem was applied to eliminate ABC ? 50

Factoring Expressions To obtain a product-of-sum form Factoring using distributive laws Theorem for factoring: Example of factoring: 68 7 A 4+ 4 B 'C 1 2 A 3 = ( A + C )( A'+ B) AC + A' BD' +A' BE + A' C ' DE = AC + A' ( BD' +BE + C ' DE) XZ X ' Y = ( A + BD' +BE + C ' DE )( A' +C ) = [ A + C ' DE + B( D' +E )]( A' +C ) X Y Z = ( A + B + C ' DE )( A + C ' DE + D' +E )( A' +C ) = ( A + B + C ' )( A + B + D)( A + B + E )( A + D' +E )( A' +C ) 51

Conversion of English Sentences to Boolean Equations × The first step in designing a logic network: − Translate English sentences to Boolean Eqns. − We must break down each sentence into phrases − And associate a Boolean variable with each phrase (possible if a phrase can have a “true”/”false” value) × Example: − Ali watches TV if it is Monday night and he has finished his homework. − F=A. B 52

Main Steps × Three main steps in designing a single-output combinational switching network: − Find a switching function which specifies the desired behavior of the network. − Find a simplified algebraic expression for the function. − Realize the simplified function using available logic elements. 53

Example × Four chairs in a row: − Occupied: ‘ 1’ − Empty: ‘ 0’ − F = ‘ 1’ iff there are no adjacent empty chairs. A B C D F = (B’C’ + A’B’ + C’D’)’ 54

Example F = (B’C’ + A’B’ + C’D’)’ F = (B+C). (A+B). (C+D) = (B+AC). (C+D) = BC + BD + ACD = BC + BD + AC 55

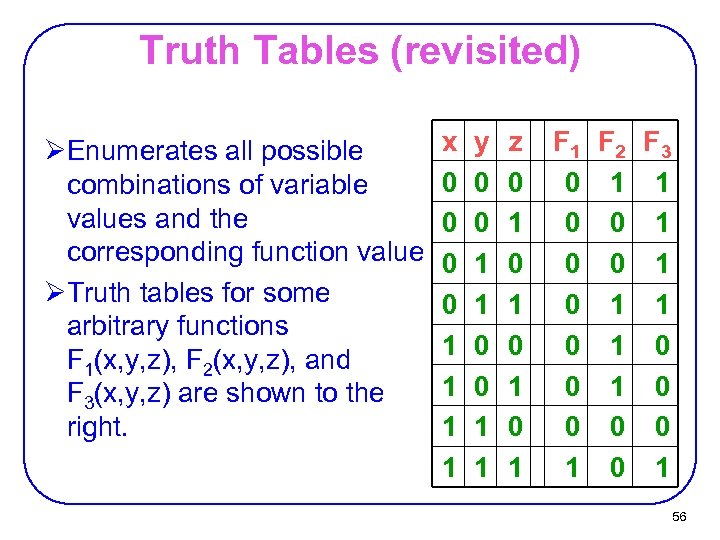
Truth Tables (revisited) ØEnumerates all possible combinations of variable values and the corresponding function value ØTruth tables for some arbitrary functions F 1(x, y, z), F 2(x, y, z), and F 3(x, y, z) are shown to the right. x 0 0 1 1 y 0 0 1 1 z 0 1 0 1 F 1 F 2 F 3 0 1 1 0 0 1 0 0 1 0 1 56

Truth Tables (cont. ) ØTruth table: a unique representation of a Boolean function ØIf two functions have identical truth tables, the functions are equivalent (and viceversa). ØTruth tables can be used to prove equality theorems. ØHowever, the size of a truth table grows exponentially with the number of variables involved. − This motivates the use of Boolean Algebra. 57

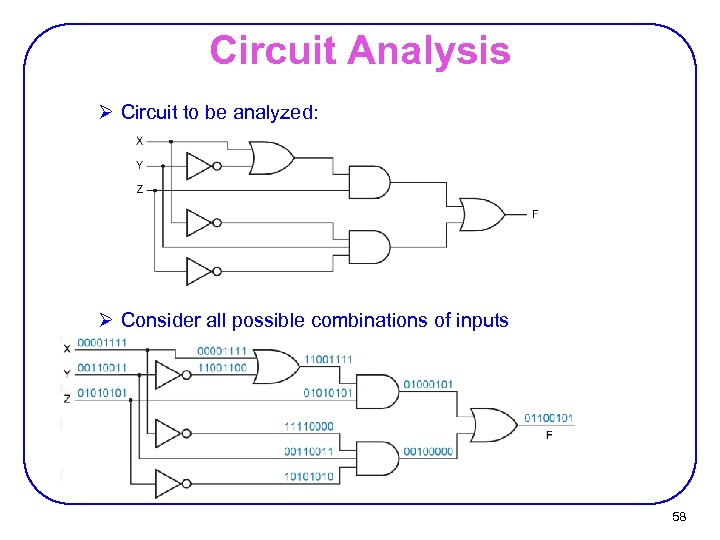
Circuit Analysis Ø Circuit to be analyzed: Ø Consider all possible combinations of inputs 58

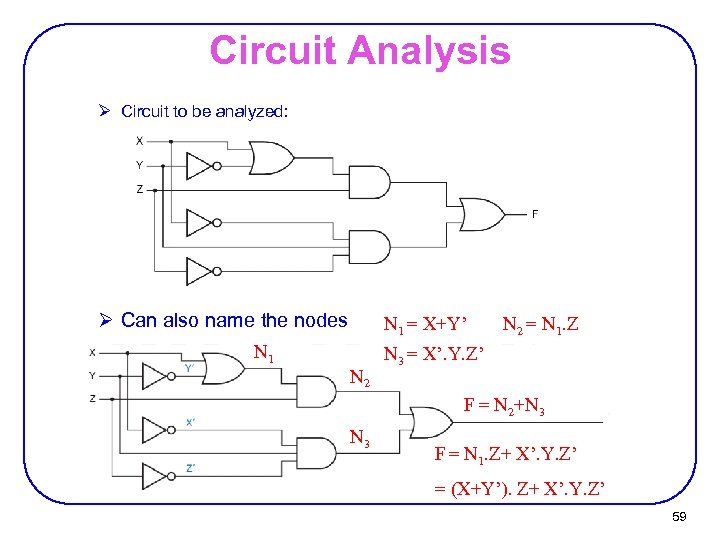
Circuit Analysis Ø Circuit to be analyzed: Ø Can also name the nodes N 1 = X+Y’ N 2 = N 1. Z N 3 = X’. Y. Z’ F = N 2+N 3 F = N 1. Z+ X’. Y. Z’ = (X+Y’). Z+ X’. Y. Z’ 59

Boolean expressions. NOT unique x y z Ø Unlike truth tables, expressions representing a Boolean function are 0 0 0 NOT unique. 0 0 1 Ø Example: − F(x, y, z) = x’ • y’ • z’ + x’ • y • z’ + x • y • z’ − G(x, y, z) = x’ • y’ • z’ + y • z’ Ø The corresponding truth tables for F() and G() are identical! Ø Thus, F() = G() 0 0 1 1 1 0 0 1 1 0 1 0 1 F 1 0 0 0 1 0 G 1 0 0 0 1 0 60

Complementation: Example • Find the complement of F(x, y, z) = xy’z’ + x’yz Ø G = F’ = (xy’z’ + x’yz)’ = (xy’z’)’ • (x’yz)’ De. Morgan = (x’+y+z) • (x+y’+z’) De. Morgan again • Note: Ø The complement of a function can also be derived by finding the function’s dual, and then complementing all of the literals 61

Complement of a Function • • ↔+ • 1↔ 0 • X ↔ X’ Ø interchange 1 s to 0 s in the truth table column showing F. Ø The complement of a function IS NOT THE SAME as the dual of a function. 62

De Morgan’s Law for a Complex Expression • To invert a function, Ø Complement all variables and constants, Ø Exchange all + ↔. • Example: ((A + B’). C’. D + EF)’ = ((A’. B) + C + D’). (E’ + F’) • Note: Ø Don’t change operator precedence 63

Shannon Theorem Ø F(x 1, x 2, …, xn) = x 1. F(1, x 2, …, xn) + x 1’. F(0, x 2, …, xn) Ø F(x 1, x 2, …, xn) = [x 1 + F(0, x 2, …, xn)]. [x 1’+ F(1, x 2, …, xn)] 64

Boolean vs. Ordinary Algebra Some of Boolean Algebra are not true for ordinary algebra Example: True in ordinary algebra Not True in Boolean algebra Some of Boolean Algebra properties are true for ordinary algebra too. Example: True in both ordinary and Boolean algebra 65

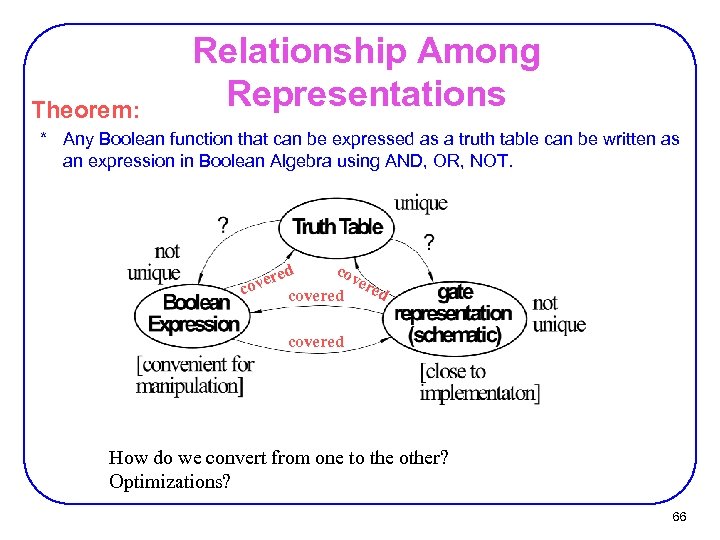
Theorem: Relationship Among Representations * Any Boolean function that can be expressed as a truth table can be written as an expression in Boolean Algebra using AND, OR, NOT. cov ered e covered How do we convert from one to the other? Optimizations? 66

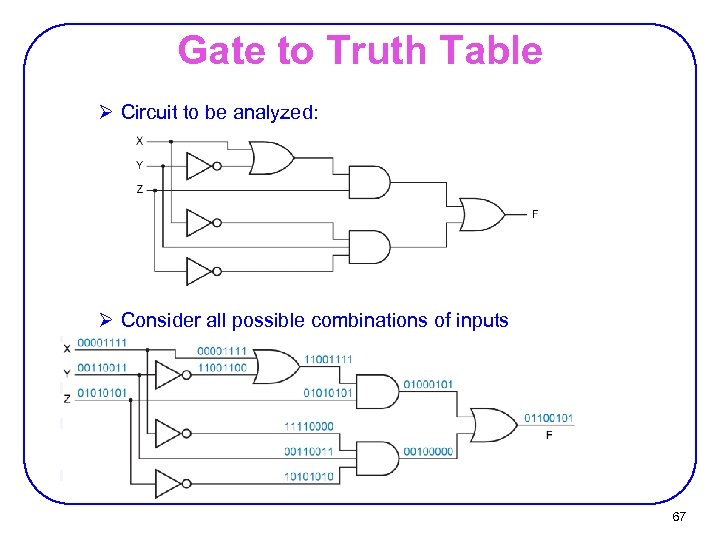
Gate to Truth Table Ø Circuit to be analyzed: Ø Consider all possible combinations of inputs 67

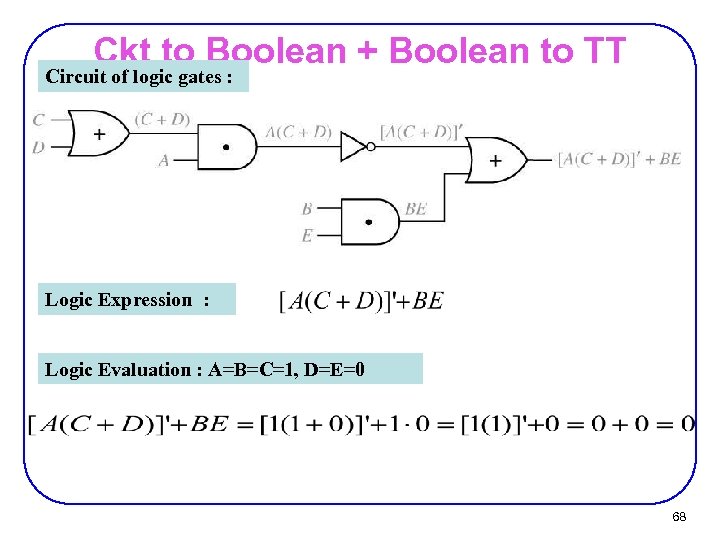
Ckt to Boolean + Boolean to TT Circuit of logic gates : Logic Expression : Logic Evaluation : A=B=C=1, D=E=0 68

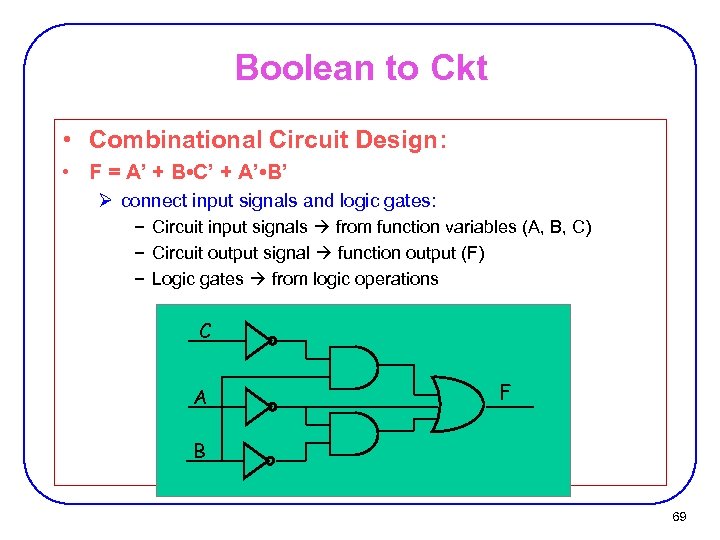
Boolean to Ckt • Combinational Circuit Design: • F = A’ + B • C’ + A’ • B’ Ø connect input signals and logic gates: − Circuit input signals from function variables (A, B, C) − Circuit output signal function output (F) − Logic gates from logic operations C A F B 69

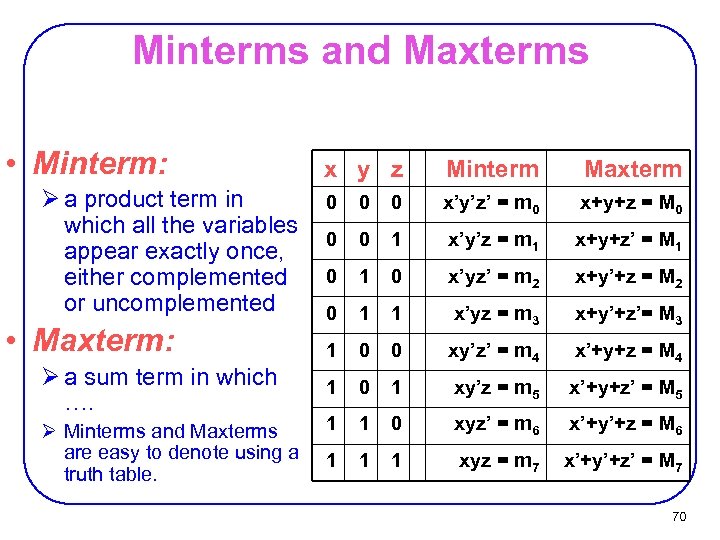
Minterms and Maxterms • Minterm: x y z Minterm Maxterm 0 0 0 x’y’z’ = m 0 x+y+z = M 0 0 0 1 x’y’z = m 1 x+y+z’ = M 1 0 x’yz’ = m 2 x+y’+z = M 2 0 1 1 x’yz = m 3 x+y’+z’= M 3 1 0 0 Ø a sum term in which …. xy’z’ = m 4 x’+y+z = M 4 1 0 1 xy’z = m 5 x’+y+z’ = M 5 Ø Minterms and Maxterms are easy to denote using a truth table. 1 1 0 xyz’ = m 6 x’+y’+z = M 6 1 1 1 xyz = m 7 x’+y’+z’ = M 7 Ø a product term in which all the variables appear exactly once, either complemented or uncomplemented • Maxterm: 70

Canonical Forms: Unique Ø Any Boolean function F( ) can be expressed as a unique sum of minterms (and a unique product of maxterms) Ø In other words, every function F() has two canonical forms: − Canonical Sum-Of-Products (sum of minterms) − Canonical Product-Of-Sums (product of maxterms) 71

Canonical Forms (cont. ) • Canonical Sum-Of-Products: ØThe minterms included are those mj such that F( ) = 1 in row j of the truth table for F( ). • Canonical Product-Of-Sums: ØThe maxterms included are those Mj such that F( ) = 0 in row j of the truth table for F( ). 72

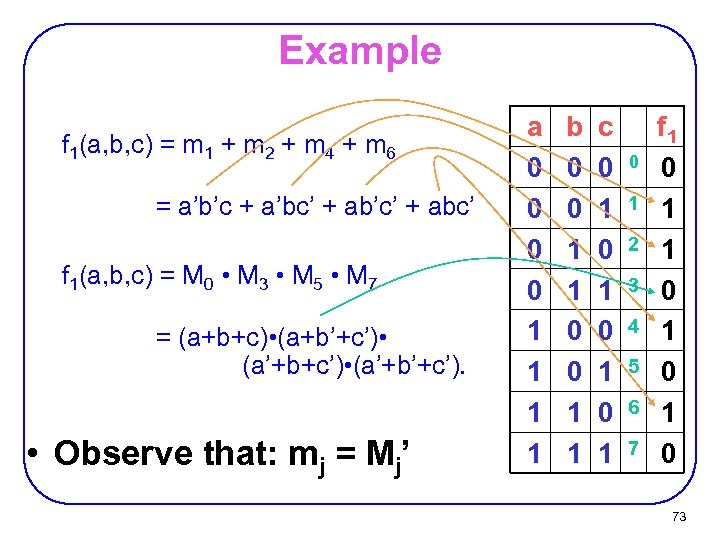
Example f 1(a, b, c) = m 1 + m 2 + m 4 + m 6 = a’b’c + a’bc’ + ab’c’ + abc’ f 1(a, b, c) = M 0 • M 3 • M 5 • M 7 = (a+b+c) • (a+b’+c’) • (a’+b’+c’). • Observe that: mj = Mj’ a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 0 1 2 3 4 5 6 7 f 1 0 1 0 1 0 73

Shorthand: ∑ and ∏ • f 1(a, b, c) = ∑ m(1, 2, 4, 6), Ø m 1+ m 2 + m 4 + m 6. • f 1(a, b, c) = ∏ M(0, 3, 5, 7), Ø M 0. M 3. M 5. M 7. Since mj = Mj’ for any j, ∑ m(1, 2, 4, 6) = ∏ M(0, 3, 5, 7) = f 1(a, b, c) 74

Conversion Between Canonical Forms Ø Replace ∑ with ∏ (or vice versa) and replace those j’s that appeared in the original form with those that do not. • Example: Ø f 1(a, b, c)= a’b’c + a’bc’ + ab’c’ + abc’ = m 1 + m 2 + m 4 + m 6 = ∑(1, 2, 4, 6) = ∏(0, 3, 5, 7) = (a+b+c) • (a+b’+c’) • (a’+b’+c’) 75

Standard Forms (NOT Unique) ØStandard forms are “like” canonical forms, − not all variables need appear in the individual product (SOP) or sum (POS) terms. • Example: Ø f 1(a, b, c) = a’b’c + bc’ + ac’ is a standard sum-of-products form Ø f 1(a, b, c) = (a+b+c) • (b’+c’) • (a’+c’) is a standard product-of-sums form. 76

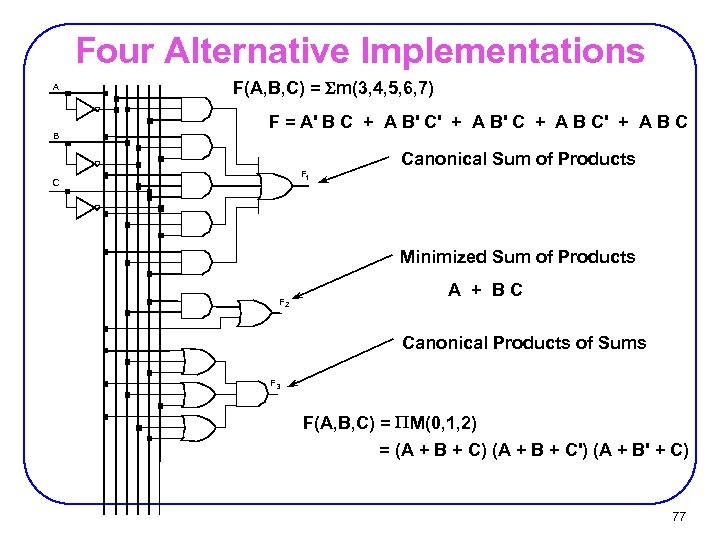
Four Alternative Implementations A B F(A, B, C) = m(3, 4, 5, 6, 7) F = A' B C + A B' C' + A B' C + A B C' + A B C Canonical Sum of Products F 1 C Minimized Sum of Products F 2 A + BC Canonical Products of Sums F 3 F(A, B, C) = M(0, 1, 2) = (A + B + C) (A + B + C') (A + B' + C) 77

Conversion of SOP from standard to canonical ØExpand non-canonical terms by inserting equivalent of 1 in each missing variable − x: (x + x’) = 1 ØRemove duplicate minterms Øf 1(a, b, c) = a’b’c + bc’ + ac’ = a’b’c + (a+a’)bc’ + a(b+b’)c’ = a’b’c + abc’ + a’bc’ + ab’c’ = a’b’c + abc’ + a’bc + ab’c’ 78

Conversion of POS from standard to canonical ØExpand noncanonical terms by adding 0 in terms of missing variables (e. g. , xx’ = 0) and using the distributive law ØRemove duplicate maxterms Øf 1(a, b, c) = (a+b+c) • (b’+c’) • (a’+c’) = (a+b+c) • (aa’+b’+c’) • (a’+bb’+c’) = (a+b+c) • (a+b’+c’) • (a’+b+c’) • (a’+b’+c’) = (a+b+c) • (a+b’+c’) • (a’+b+c’) 79

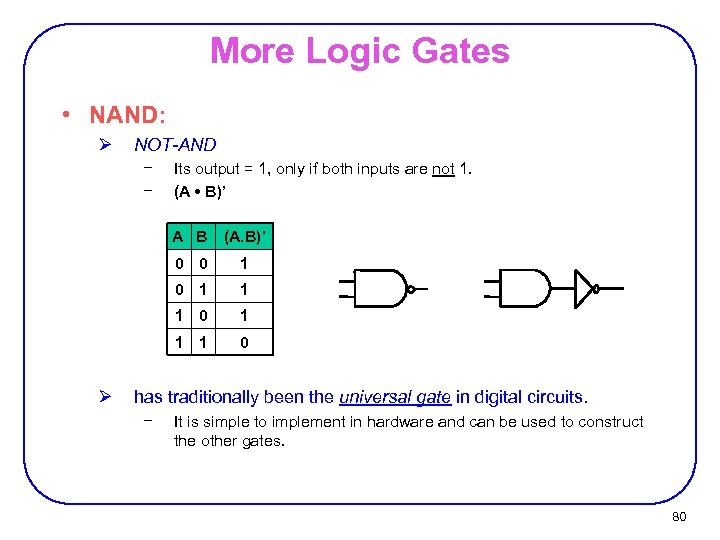
More Logic Gates • NAND: Ø NOT-AND − − Its output = 1, only if both inputs are not 1. (A • B)’ A B (A. B)’ 0 0 0 1 1 1 Ø 1 0 has traditionally been the universal gate in digital circuits. − It is simple to implement in hardware and can be used to construct the other gates. 80

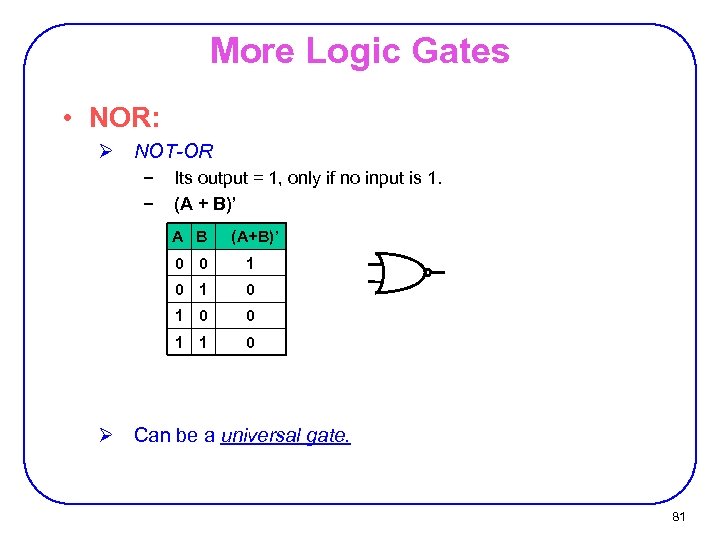
More Logic Gates • NOR: Ø NOT-OR − − Its output = 1, only if no input is 1. (A + B)’ A B (A+B)’ 0 0 1 0 1 0 0 1 1 0 Ø Can be a universal gate. 81

More Logic Gates • XOR: Ø Inequality − − Its output = 1, only if exactly one input is 1. (A + B) O A B A XOR B 0 0 1 1 1 0 82

More Logic Gates • 3 -input XOR: − − Its output = 1, only if one or three inputs are 1. (A + B O C) O + A B C A XOR B XOR C 0 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 83

More Logic Gates • XNOR: Ø Equality − − Its output = 1, only both inputs are equal. (A + B)’ O A B A XNOR B 0 0 1 0 1 0 0 1 1 1 84

Theorems for XOR 85

Problem Solving Ø More often, we describe a logic function using the Englishlanguage connectives “and, ” “or, ” and “not. ” • Example: An alarm circuit Ø The ALARM output is 1 if the PANIC input is 1, or if the ENABLE input is 1, the EXITING input is 0, and the house is not secure; Ø The house is secure if the WINDOW, DOOR, and GARAGE inputs are all 1. ALARM = PANIC + ENABLE. EXITING¢. SECURE¢ SECURE = WINDOW. DOOR. GARAGE ALARM = PANIC + ENABLE. EXITING¢. (WINDOW. DOOR. GARAGE)¢ 86

Problem Solving Ø Sometimes we have to work with imprecise word descriptions of logic functions, • Example: Ø “The ERROR output should be 1 if the GEAR, CLUTCH, and BRAKE inputs are inconsistent. ” Ø In this situation, the truth-table approach is best because it allows us to determine the output required for every input combination, based on our knowledge and understanding of the problem environment − e. g. , the brakes cannot be applied unless the gear is down. 87

Example • A 4 -bit Prime Number Detector )31 , 11 , 7 , 5 , 3 , 2 , 1(0 F = SN 3, N 2, N 1, N +0 =N 3¢. N 2¢. N 1¢. N 0 + N 3¢. N 2¢. N 1. N 0¢ + N 3¢. N 2¢. N 1. N + 0 N 3¢. N 2. N 1¢. N 0 + N 3¢. N 2. N 1. N 0 + N 3. N 2¢. N 1. N 0 N 3. N 2. N 1¢. N + 0 =N 3¢. N 1¢. N 0 + N 3¢. N 2¢. N 1 + N 3¢. N 2. N 1. N 0 N 3. N 2¢. N 1. N 0 + N 3. N 2. N 1¢. N • ﺑﺮﺍﻱ ﻋﺒﺎﺭﺍﺕ پﻴچﻴﺪﻩ، کﺎﺭ ﺑﻬﻴﻨﻪ ﺳﺎﺯﻱ ﺳﺨﺖ ﺗﺮ ﻣﻴﺸﻮﺩ. …= • ﺭﻭﺷﻲ ﺳﻴﺴﺘﻤﺎﺗﻴک ﻭ آﺴﺎﻥ ﺗﺮ: ﻧﻘﺸﺔ کﺎﺭﻧﻮ • ﺷﻤﺎ ﺭﺍ ﺍﺯ ﺟﺒﺮ ﺑﻮﻝ ﺑﻲ ﻧﻴﺎﺯ ﻧﻤﻲ کﻨﺪ. 88

Incompletely Specified Functions • Don’t Care: Ø Ø We don’t care about the output values for some intput patterns. this fact can be exploited during circuit minimization! • Example: Ø BCD incrementer: Off-set of W On-set of W Don't care (DC) set of W These input patterns should never be encountered in practice associated output values are "Don't Cares" 89

Don't Cares and Canonical Forms Canonical Representations of the BCD Incrementer: Z = m 0 + m 2 + m 4 + m 6 + m 8 + d 10 + d 11 + d 12 + d 13 + d 14 + d 15 Z = m(0, 2, 4, 6, 8) + d(10, 11, 12 , 13, 14, 15) Z = M 1 • M 3 • M 5 • M 7 • M 9 • D 10 • D 11 • D 12 • D 13 • D 14 • D 15 Z= M(1, 3, 5, 7, 9) • D(10, 11, 12, 13, 14 , 15) 90