2f8c159cd5ca5f1d7e6a727f80dea75e.ppt
- Количество слайдов: 113

ﺑﺴﻤﻪﺗﻌﺎﻟﻲ Digital Image Processing Image Compression (Chapter 8) H. R. Pourreza

Image Compression? • The problem of reducing the amount of data required to represent a digital image. • From a mathematical viewpoint: transforming a 2 -D pixel array into a statistically uncorrelated data set. H. R. Pourreza

Why do We Need Compression? • For data STORAGE and data TRANSMISSION • • • DVD Remote Sensing Video conference FAX Control of remotely piloted vehicle • The bit rate of uncompressed digital cinema data exceeds 1 Gbps H. R. Pourreza
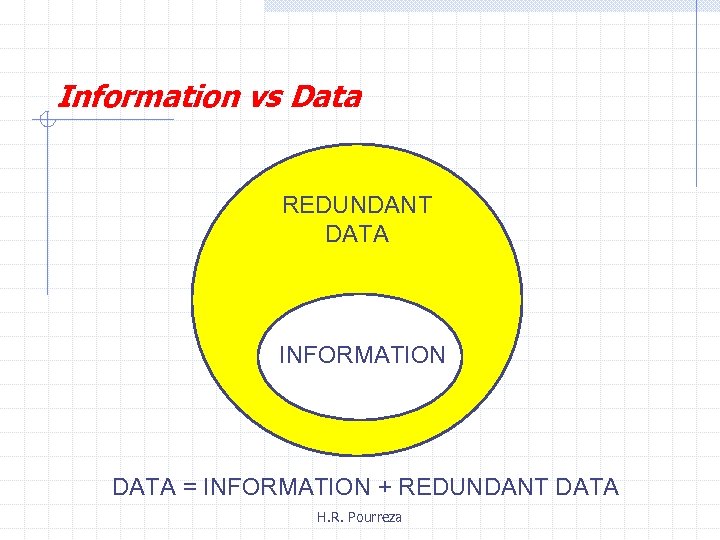
Information vs Data REDUNDANT DATA INFORMATION DATA = INFORMATION + REDUNDANT DATA H. R. Pourreza

Why Can We Compress? • Spatial redundancy • Neighboring pixels are not independent but correlated § Temporal redundancy H. R. Pourreza

Fundamentals • Basic data redundancies: 1. 2. 3. Coding redundancy Inter-pixel redundancy Psycho-visual redundancy H. R. Pourreza

Coding Redundancy Let us assume, that a discrete random variable rk in the interval [0, 1] represent the gray level of an image: If the number of bits used to represent each value of rk is l(rk), then the average number of bits required to represent each pixel: The total number bits required to code an Mx. N image: H. R. Pourreza

Coding Redundancy Compression ratio: Relative data redundancy: H. R. Pourreza
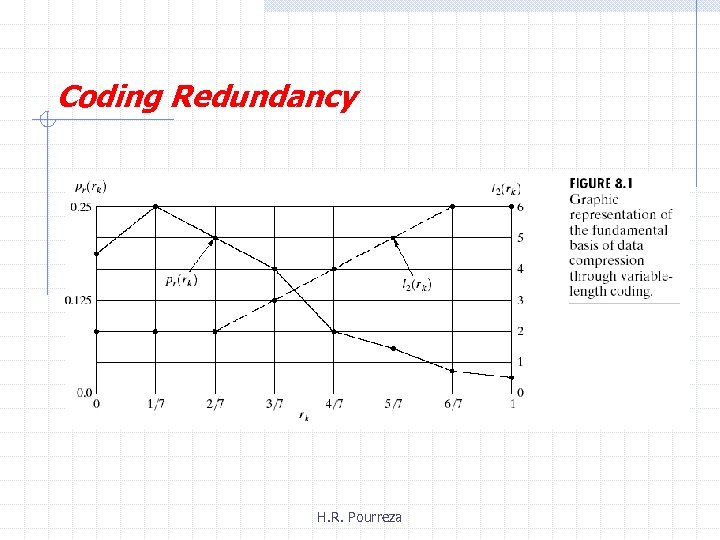
Coding Redundancy H. R. Pourreza
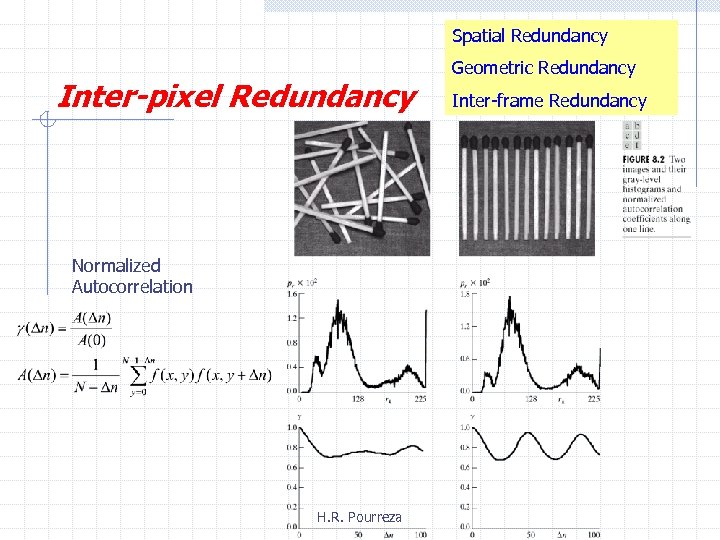
Spatial Redundancy Inter-pixel Redundancy Normalized Autocorrelation H. R. Pourreza Geometric Redundancy Inter-frame Redundancy
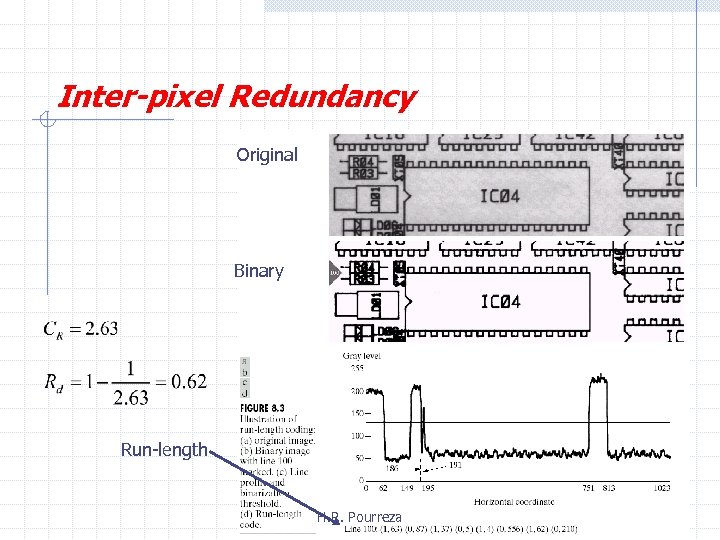
Inter-pixel Redundancy Original Binary Run-length H. R. Pourreza
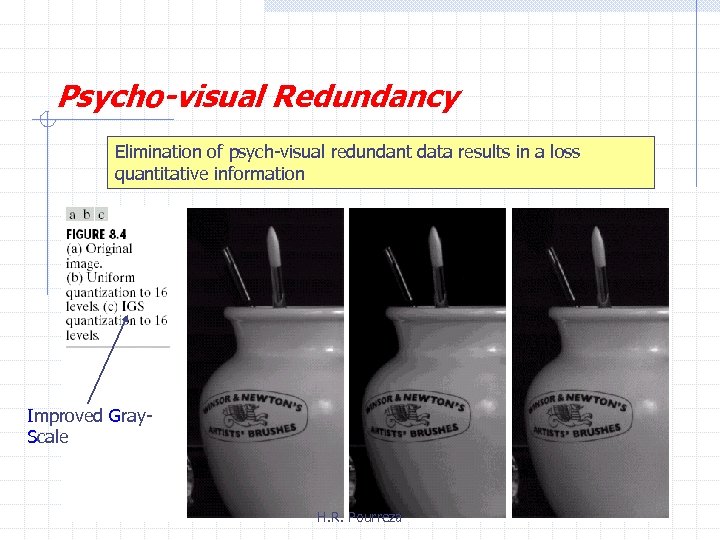
Psycho-visual Redundancy Elimination of psych-visual redundant data results in a loss quantitative information Improved Gray. Scale H. R. Pourreza

Psycho-visual Redundancy IGS Quantization H. R. Pourreza

Fidelity Criteria The general classes of criteria : 1. Objective fidelity criteria 2. Subjective fidelity criteria H. R. Pourreza

Fidelity Criteria Objective fidelity: Level of information loss can be expressed as a function of the original and the compressed and subsequently decompressed image. Root-mean-square error Mean-square signal -to-noise ratio H. R. Pourreza

Fidelity Criteria Subjective fidelity (Viewed by Human): • By absolute rating • By means of side-by-side comparison of H. R. Pourreza and
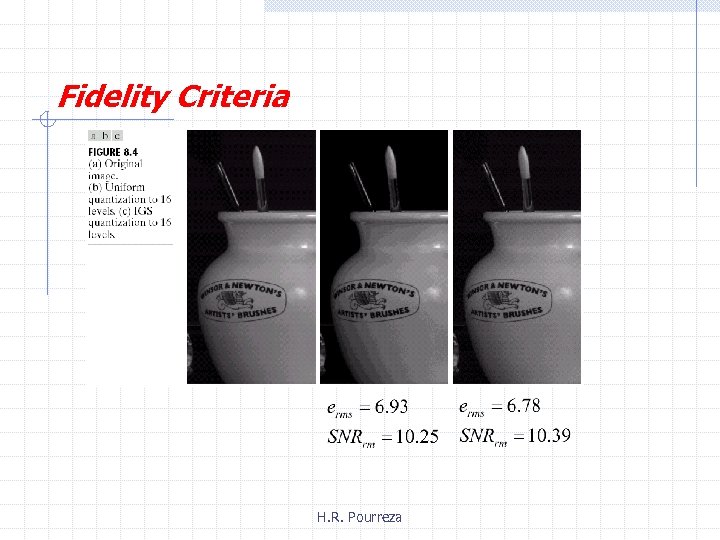
Fidelity Criteria H. R. Pourreza
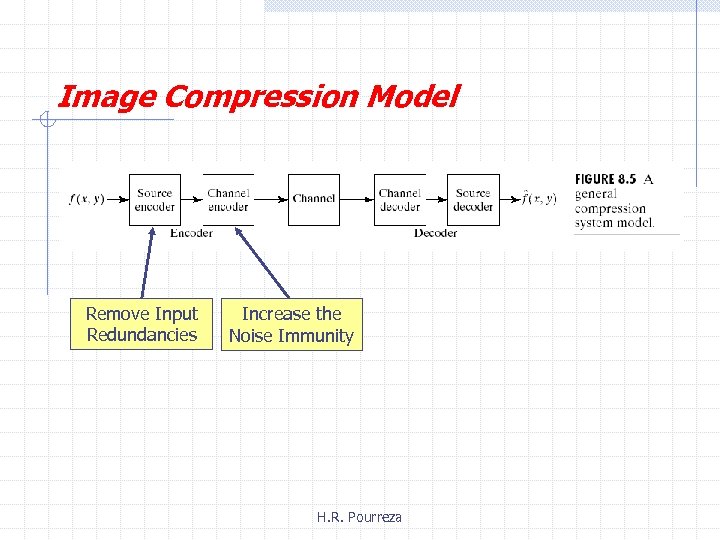
Image Compression Model Remove Input Redundancies Increase the Noise Immunity H. R. Pourreza
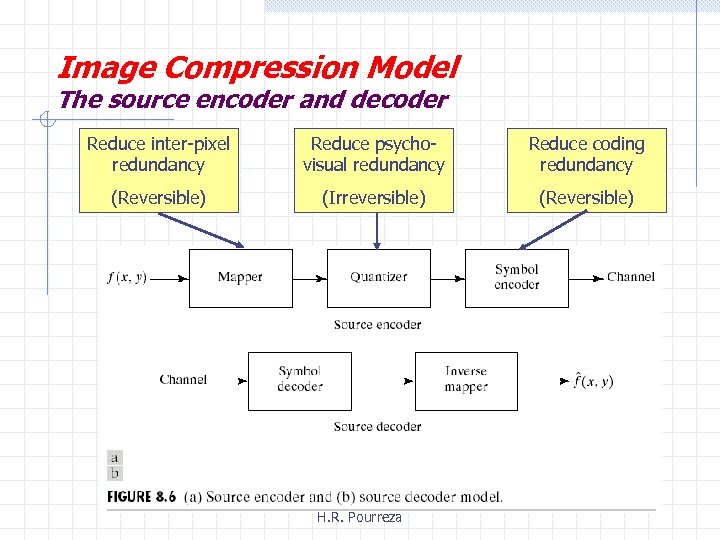
Image Compression Model The source encoder and decoder Reduce inter-pixel redundancy Reduce psychovisual redundancy Reduce coding redundancy (Reversible) (Irreversible) (Reversible) H. R. Pourreza

Image Compression Model The channel encoder and decoder Channel encoder and decoder designed to reduce the impact of channel noise by inserting a controlled form of redundancy into the source encoded data. Example) 7 -bit Hamming (7, 4) code: h 1 h 2 … h 6 h 7 : h 3=b 3 c 1=b 1 b 3 b 5 b 7 h 5=b 2 c 2=b 2 b 3 b 6 b 7 h 6=b 1 c 3=b 4 b 5 b 6 b 7 h 7=b 0 h 1=b 3 b 2 b 0 h 2=b 3 b 1 b 0 h 4=b 2 b 1 b 0 H. R. Pourreza

Measuring Information A random event E that occurs with probability P(E) is said to contain: units of information. The quantity of I(E) often is called Self. Information of E. If the base m logarithm is used, then the measurement is said to be in m-ary units. Examples: P(E)=1 P(E)=0. 99 P(E)=1/2 I(E)=0 (No information) (some small amount of information) H. R. Pourreza

Measuring Information source generate a random sequence of symbols. If k source symbols are generated, the law of large numbers stipulates that, for a sufficiently large value of k, symbol aj will be output k. P(aj). Thus the average self information obtain from k output is: The average information per source output is: uncertainty or entropy of source. H. R. Pourreza

Classification § Lossless compression § § lossless compression for legal and medical documents, computer programs exploit only code and inter-pixel redundancy § Lossy compression § § digital image and video where some errors or loss can be tolerated exploit both code and inter-pixel redundancy and sychovisual perception properties H. R. Pourreza

Error-Free Compression Applications: • Archive of medical or business documents • Satellite imaging • Digital radiography They provide: Compression ratio of 2 to 10. H. R. Pourreza

Error-Free Compression Variable-length Coding Huffman coding (optimal code) H. R. Pourreza

Error-Free Compression Variable-length Coding Huffman coding H. R. Pourreza
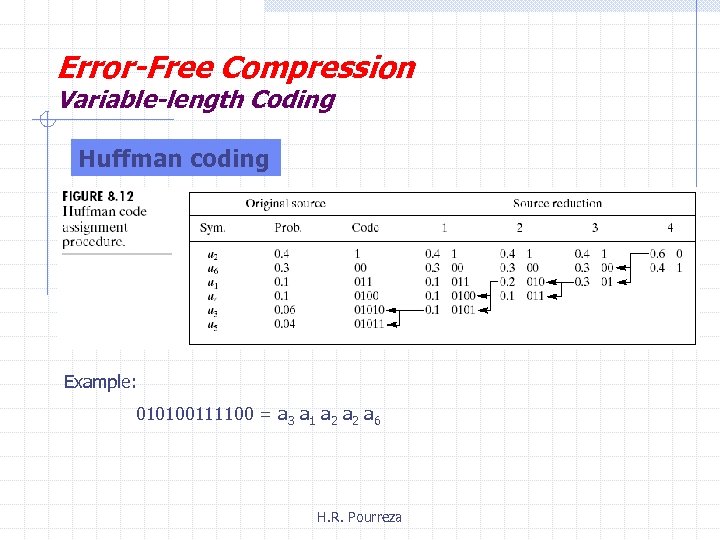
Error-Free Compression Variable-length Coding Huffman coding Example: 010100111100 = a 3 a 1 a 2 a 6 H. R. Pourreza

Error-Free Compression Variable-length Coding Huffman coding § Variable length code whose length is inversely proportional to that character’s frequency § must satisfy non-prefix property to be uniquely decodable § two pass algorithm § § first pass accumulates the character frequency and generate codebook second pass does compression with the codebook H. R. Pourreza

Error-Free Compression Variable-length Coding Huffman coding § create codes by constructing a binary tree § § 1. consider all characters as free nodes 2. assign two free nodes with lowest frequency to a parent nodes with weights equal to sum of their frequencies 3. remove the two free nodes and add the newly created parent node to the list of free nodes 4. repeat step 2 and 3 until there is one free node left. It becomes the root of tree H. R. Pourreza
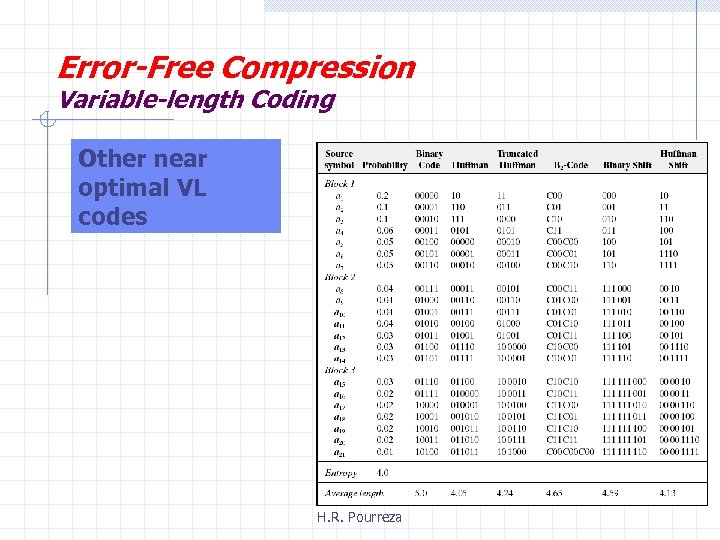
Error-Free Compression Variable-length Coding Other near optimal VL codes H. R. Pourreza
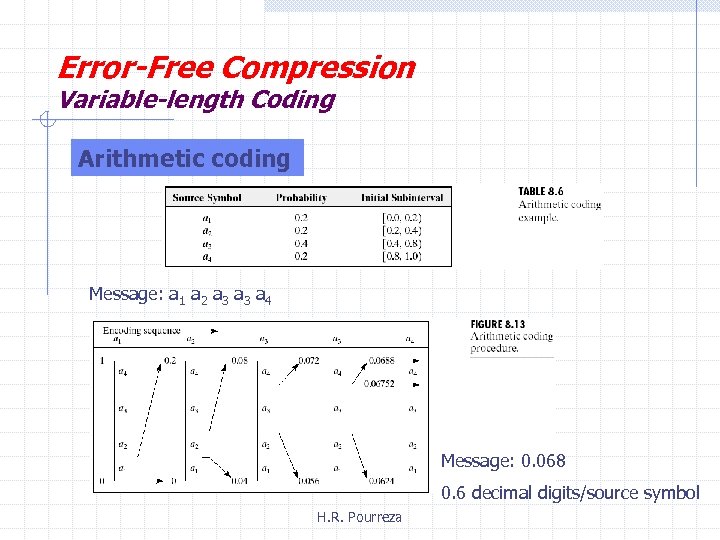
Error-Free Compression Variable-length Coding Arithmetic coding Message: a 1 a 2 a 3 a 4 Message: 0. 068 0. 6 decimal digits/source symbol H. R. Pourreza

Error-Free Compression Variable-length Coding Arithmetic coding § take in complete data stream and output one specific codeword which is floating point number between 0 and 1 § two pass algorithm § § first pass computes characters’ frequency and constructs probability table with ranges assigned to each entry of the table second pass does actual compression § first character of input stream constrains output number to its corresponding range, and the range of next character of input stream further constrains the number, and so on. § decoding is reverse of encoding § achieve higher compression ratio than Huffman, but computationally expensive H. R. Pourreza
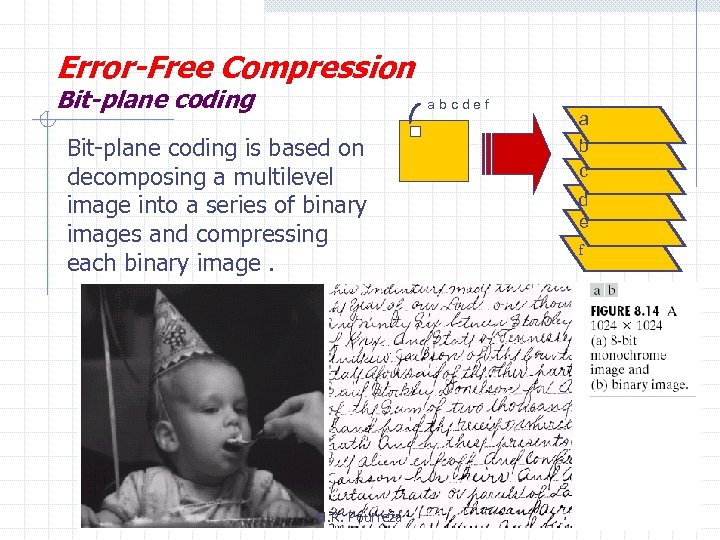
Error-Free Compression Bit-plane coding abcdef Bit-plane coding is based on decomposing a multilevel image into a series of binary images and compressing each binary image. H. R. Pourreza a b c d e f

Error-Free Compression Binary Bit-planes Bit-plane coding Bit-plane decomposition H. R. Pourreza Gray Bit-planes

Error-Free Compression Binary Bit-planes Bit-plane coding Bit-plane decomposition H. R. Pourreza Gray Bit-planes

Error-Free Compression Bit-plane coding • Constant area Coding • One-dimensional run-length coding Average values of black and white run lengths H. R. Pourreza

Error-Free Compression Bit-plane coding Two-dimensional RLC Relative Address Coding (RAC) is based on tracking the binary transitions. H. R. Pourreza

Error-Free Compression Bit-plane coding Contour tracing and coding Represent a contour: 1. By a set of boundary points 2. By a single boundary point and a set of directional (Direct contour tracing) H. R. Pourreza

Error-Free Compression Bit-plane coding Contour tracing and coding Predictive Differential Quantization (PDQ) and Double Delta Coding (DDQ) H. R. Pourreza
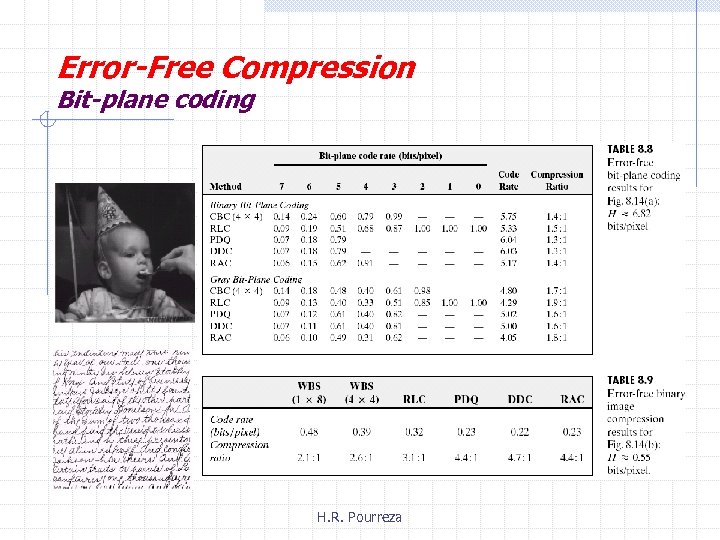
Error-Free Compression Bit-plane coding H. R. Pourreza
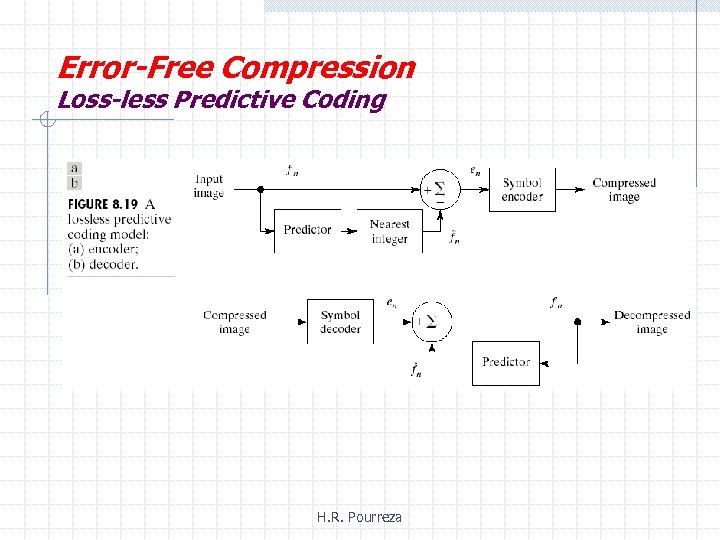
Error-Free Compression Loss-less Predictive Coding H. R. Pourreza

Error-Free Compression Loss-less Predictive Coding In most cases, the prediction is formed by a linear combination of m previous pixels. That is: 1 -D Linear Predictive coding: m is the order of linear predictor H. R. Pourreza
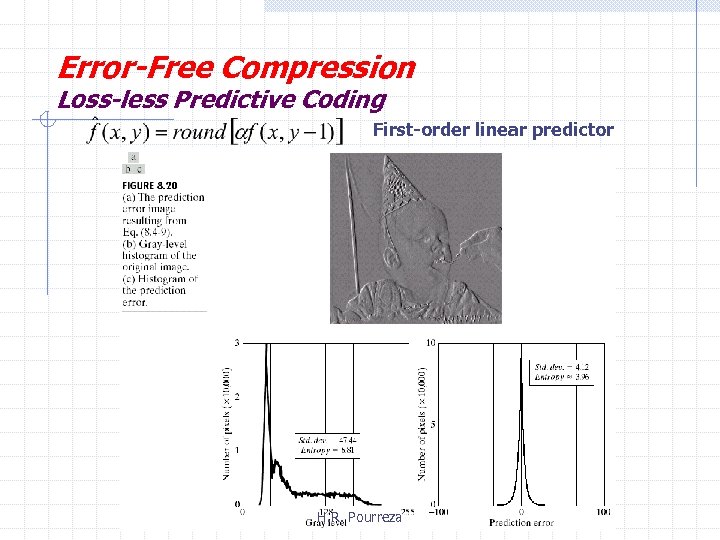
Error-Free Compression Loss-less Predictive Coding First-order linear predictor H. R. Pourreza

Lossy Compression Lossy encoding is based on the concept of compromising the accuracy of the reconstructed image in exchange for increased compression. Lossy encoding techniques are capable of reproducing recognizable mono-chrome images from data that have been compressed by more than 100: 1 and images that are virtually indistinguishable from the original at 10: 1 to 50: 1. Lossy Compression: 1. Spatial domain methods 2. Transform coding H. R. Pourreza

Lossy Compression Lossy Predictive Coding • Predictive Coding : transmit the difference between estimate of future sample & the sample itself. • • Delta modulation DPCM Adaptive predictive coding Differential frame coding H. R. Pourreza
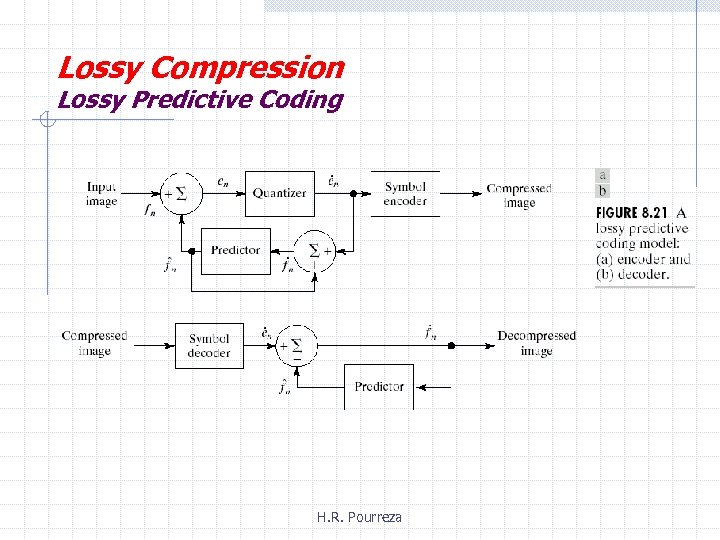
Lossy Compression Lossy Predictive Coding H. R. Pourreza

Lossy Compression Lossy Predictive Coding – Delta Modulation (DM) H. R. Pourreza
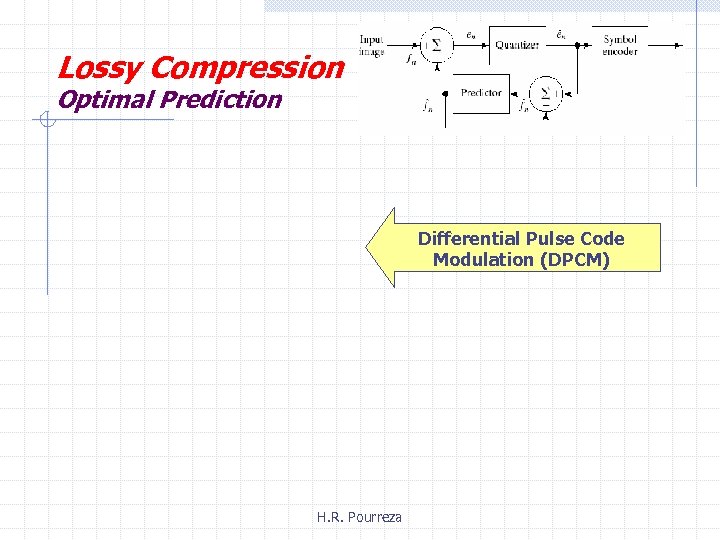
Lossy Compression Optimal Prediction Differential Pulse Code Modulation (DPCM) H. R. Pourreza
Lossy Compression Optimal Prediction Error Pred. #1 Pred. #2 Pred. #3 Pred. #4 H. R. Pourreza

Lossy Compression Optimal Prediction H. R. Pourreza
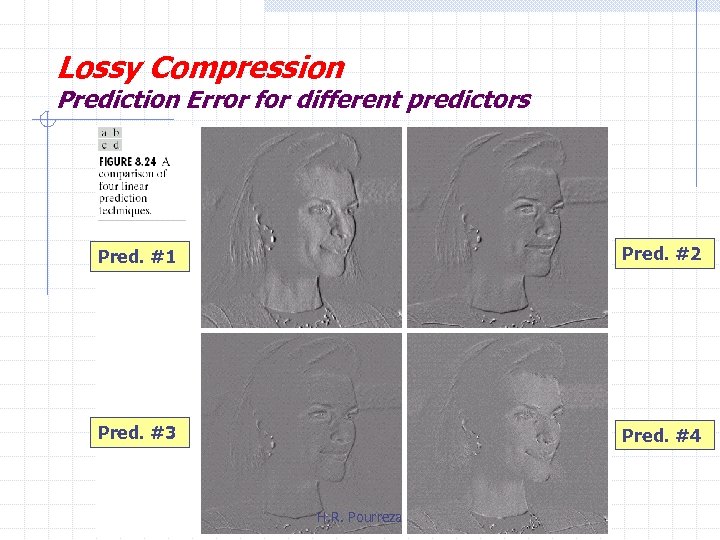
Lossy Compression Prediction Error for different predictors Pred. #1 Pred. #2 Pred. #3 Pred. #4 H. R. Pourreza
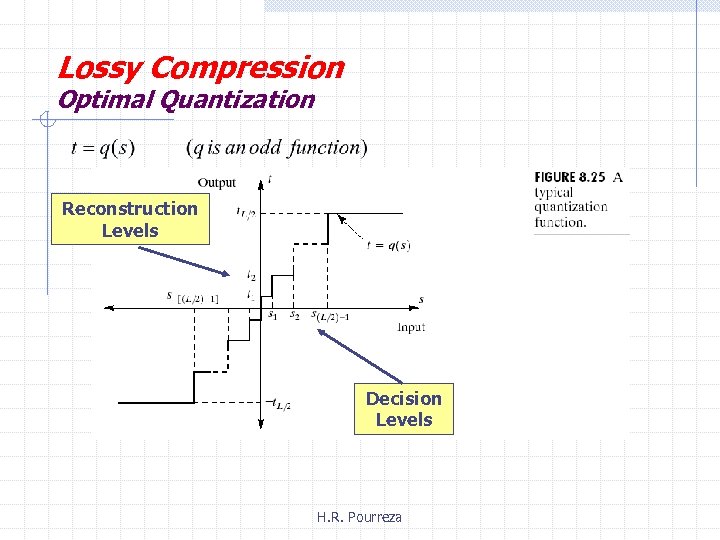
Lossy Compression Optimal Quantization Reconstruction Levels Decision Levels H. R. Pourreza

Lossy Compression Optimal Quantization Minimization of the mean-square quantization error Additional constraint for optimum uniform quantizer: H. R. Pourreza

Lossy Compression Optimal Quantization Unit variance Laplacian probability density function As this table constructed for a unit variance distribution, the reconstruction and decision levels for the case of are obtained by multiplying the tabulated values by the standard deviation 0 of the probability density function H. R. Pourreza
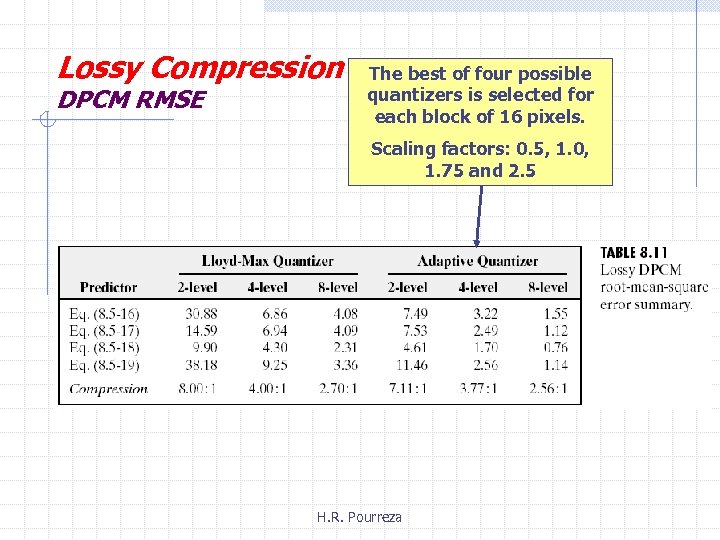
Lossy Compression DPCM RMSE The best of four possible quantizers is selected for each block of 16 pixels. Scaling factors: 0. 5, 1. 0, 1. 75 and 2. 5 H. R. Pourreza

Lossy Compression DPCM result images 2 -level Lloyd-Max quantizer 2 -level adaptive quantizer 1. 0 bits/pixel 1. 125 bits/pixel 4 -level Lloyd-Max quantizer 4 -level adaptive quantizer 2. 0 bits/pixel 2. 125 bits/pixel 8 -level Lloyd-Max quantizer 8 -leveladaptive quantizer 3. 0 bits/pixel 3. 125 bits/pixel H. R. Pourreza

Lossy Compression DPCM Prediction Error 2 -level Lloyd-Max quantizer 2 -level adaptive quantizer 1. 0 bits/pixel 1. 125 bits/pixel 4 -level Lloyd-Max quantizer 4 -level adaptive quantizer 2. 0 bits/pixel 2. 125 bits/pixel 8 -level Lloyd-Max quantizer 8 -leveladaptive quantizer 3. 0 bits/pixel 3. 125 bits/pixel H. R. Pourreza
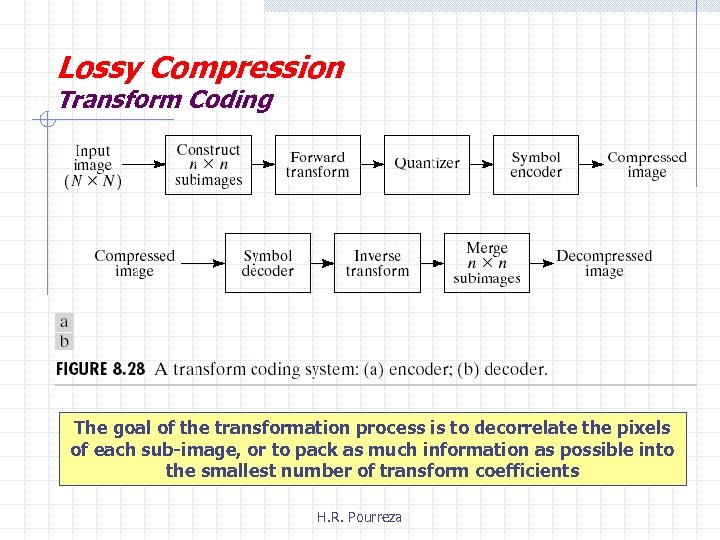
Lossy Compression Transform Coding The goal of the transformation process is to decorrelate the pixels of each sub-image, or to pack as much information as possible into the smallest number of transform coefficients H. R. Pourreza

Lossy Compression Transform Coding Forward kernel is Separable if: Forward kernel is Symmetric if: H. R. Pourreza

Lossy Compression Transform Coding Discrete Fourier Transform (DFT): Walsh-Hadamard Transform (WHT): bk(z) is the kth bit (from right to left) in the binary representation of z. H. R. Pourreza

Lossy Compression Transform Coding H. R. Pourreza

Lossy Compression Transform Coding Discrete Cosin Transform (DCT): H. R. Pourreza

Lossy Compression Transform Coding H. R. Pourreza

Lossy Compression Transform Coding 1. Dividing the image into sub-images of size 8 x 8 DFT rmse=1. 28 WHT rmse=0. 86 DCT rmse=0. 68 2. Representing each subimage using one of the transforms 3. Truncating 50% of the resulting coefficients 4. Taking the inverse Transform of the truncated coefficients H. R. Pourreza
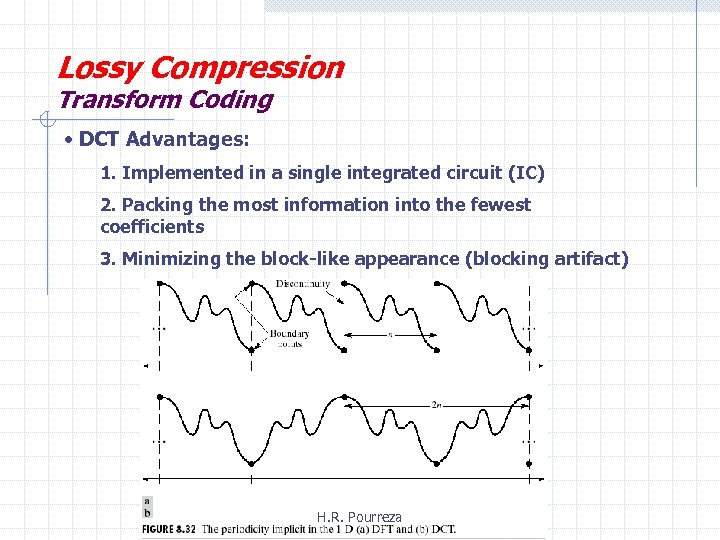
Lossy Compression Transform Coding • DCT Advantages: 1. Implemented in a single integrated circuit (IC) 2. Packing the most information into the fewest coefficients 3. Minimizing the block-like appearance (blocking artifact) H. R. Pourreza
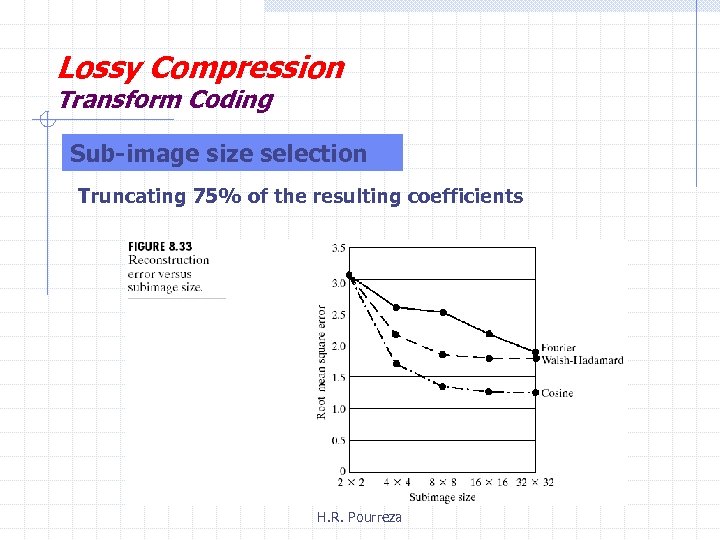
Lossy Compression Transform Coding Sub-image size selection Truncating 75% of the resulting coefficients H. R. Pourreza

Lossy Compression Transform Coding Truncating 75% of the resulting coefficients. Sub-images size: 8 x 8 4 x 4 2 x 2 H. R. Pourreza
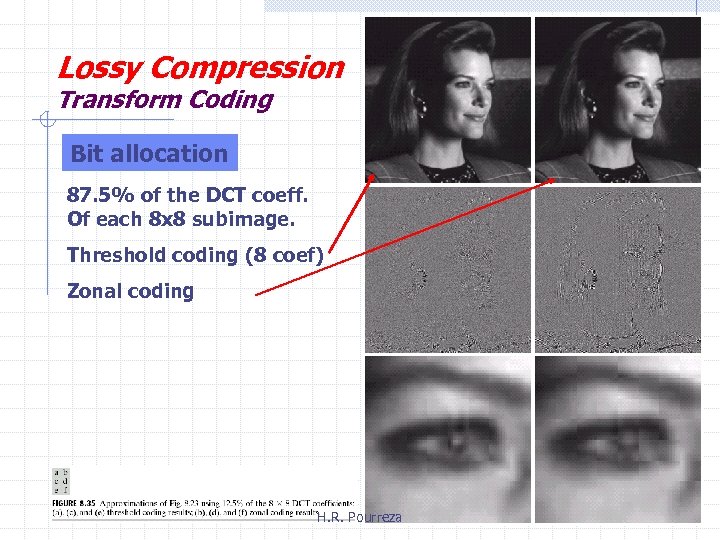
Lossy Compression Transform Coding Bit allocation 87. 5% of the DCT coeff. Of each 8 x 8 subimage. Threshold coding (8 coef) Zonal coding H. R. Pourreza
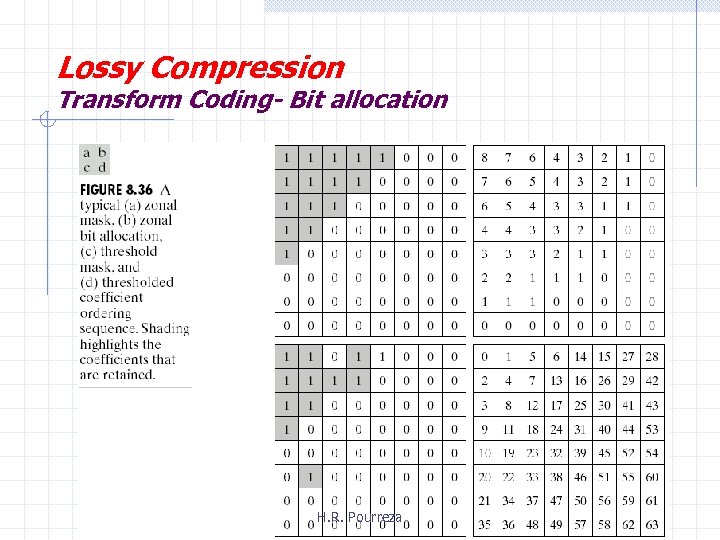
Lossy Compression Transform Coding- Bit allocation H. R. Pourreza

Lossy Compression Transform Coding- Bit allocation • Zonal coding 1. Fixed number of bits / coefficient 1. - Coefficients are normalized by their standard deviations and uniformly quantized 2. Fixed number of bits is distributed among the coefficients unequally. - A quantizer such as an optimal Lloyed-Max is designed for each coeff. : - DC coeff. Is modeled by Rayleigh density func. - The remaining coeff. Are modeled by Laplcian or Gaussian H. R. Pourreza

Lossy Compression Transform Coding- Bit allocation • Threshold coding 1. Single global threshold 2. Different threshold for each subimage (N-Largest coding) 3. Threshold can be varied as a function of the location of each coeff. H. R. Pourreza

Lossy Compression Transform Coding Bit allocation 34: 1 67: 1 rmse: 3. 42 rmse: 6. 33 H. R. Pourreza
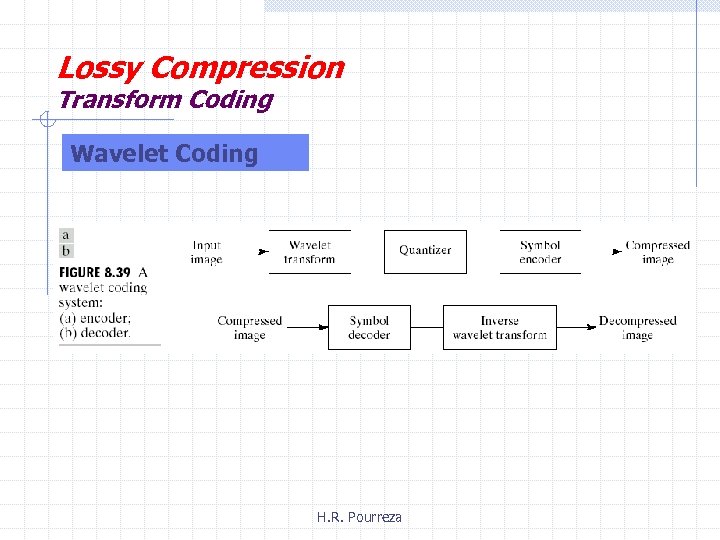
Lossy Compression Transform Coding Wavelet Coding H. R. Pourreza

Lossy Compression Transform Coding Wavelet Coding 34: 1 67: 1 rmse: 2. 29 rmse: 2. 96 No blocking H. R. Pourreza
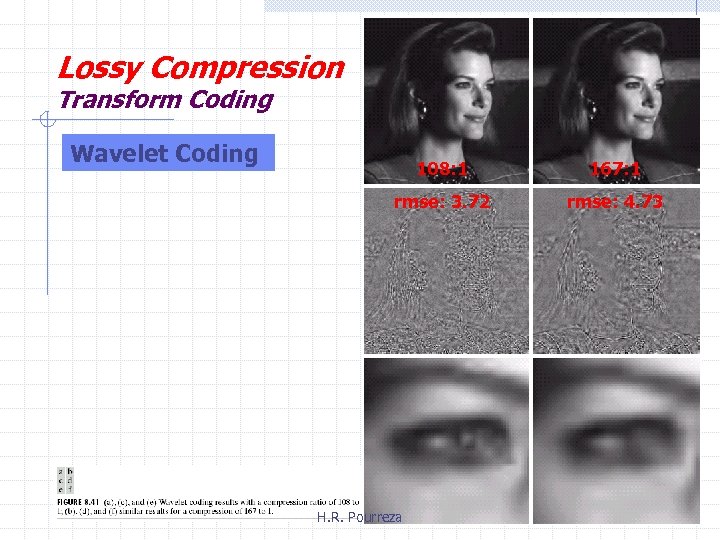
Lossy Compression Transform Coding Wavelet Coding 108: 1 167: 1 rmse: 3. 72 rmse: 4. 73 H. R. Pourreza
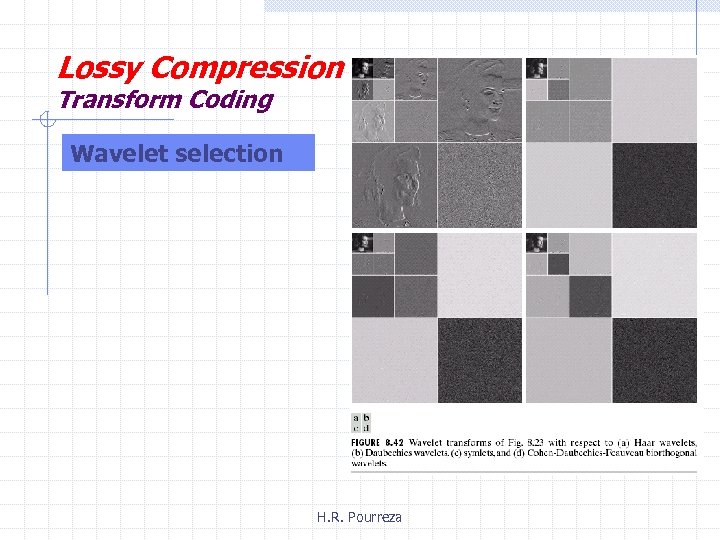
Lossy Compression Transform Coding Wavelet selection H. R. Pourreza
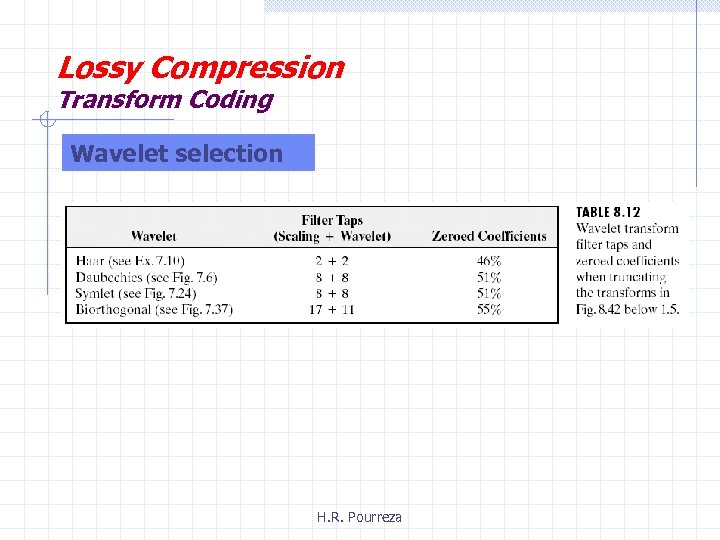
Lossy Compression Transform Coding Wavelet selection H. R. Pourreza
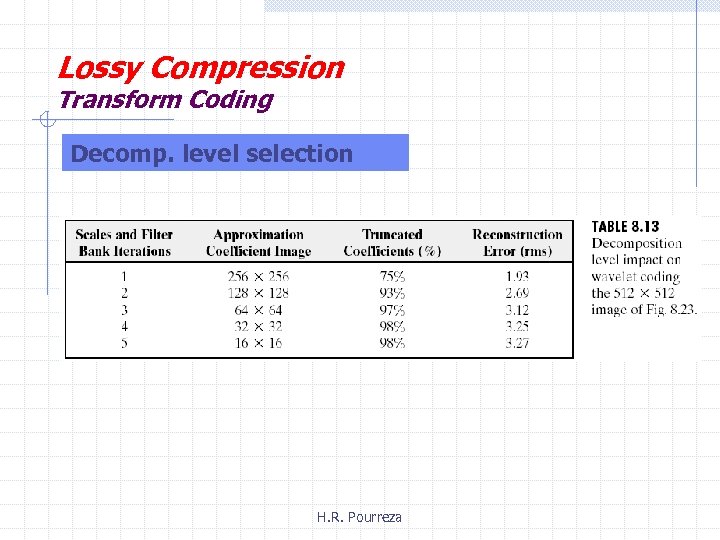
Lossy Compression Transform Coding Decomp. level selection H. R. Pourreza
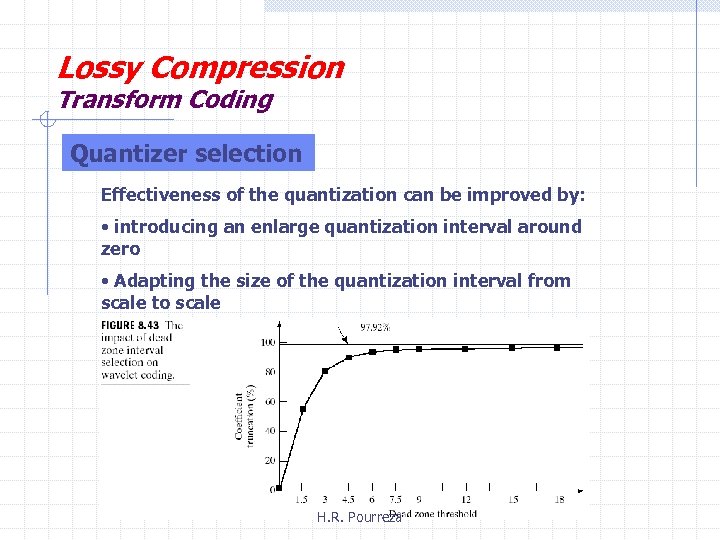
Lossy Compression Transform Coding Quantizer selection Effectiveness of the quantization can be improved by: • introducing an enlarge quantization interval around zero • Adapting the size of the quantization interval from scale to scale H. R. Pourreza

Image Compression Standards Why Do We Need International Standards? § International standardization is conducted to achieve inter-operability. § Only syntax and decoder are specified. § Encoder is not standardized and its optimization is left to the manufacturer. § Standards provide state-of-the-art technology that is developed by a group of experts in the field. § Not only solve current problems, but also anticipate the future application requirements. § Most of the standards are sanction by the International Standardization Organization (ISO) and the Consultative Committee of the International Telephone and Telegraph (CCITT) H. R. Pourreza

Image Compression Standards Binary Image Compression Standards CCITT Group 3 and 4 § They are designed as FAX coding methods. § The Group 3 applies a non-adaptive 1 -D run length coding and optionally 2 -D manner. § Both standards use the same non-adaptive 2 -D coding approach, similar to RAC technique. § They sometime result in data expansion. Therefore, the Joint Bilevel Imaging Group (JBIG), has adopted several other binary compression standards, JBIG 1 and JBIG 2. H. R. Pourreza

Image Compression Standards Binary Image Comp. Stan. – 1 -D Compression § Each line of image is encode as a series of variable- length code words that present the run lengths of the alternative white and black runs in a left-to-right scan of the line. § A unique end-of-line (EOL) code word 0000001 is used to terminated each line. H. R. Pourreza
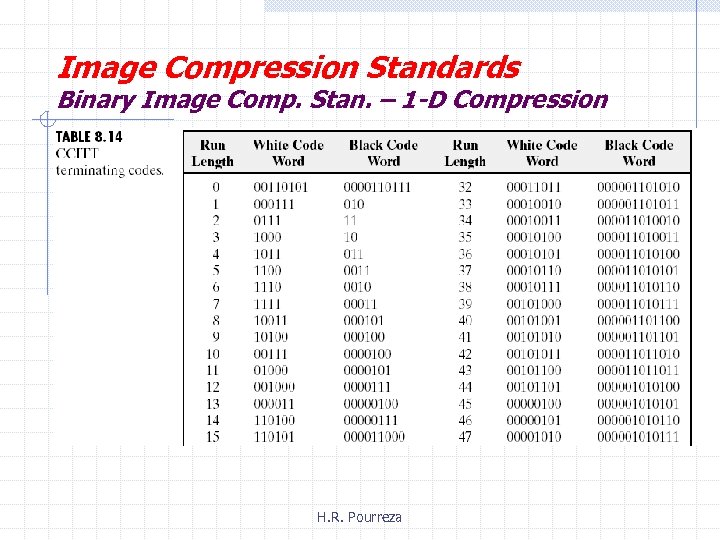
Image Compression Standards Binary Image Comp. Stan. – 1 -D Compression H. R. Pourreza
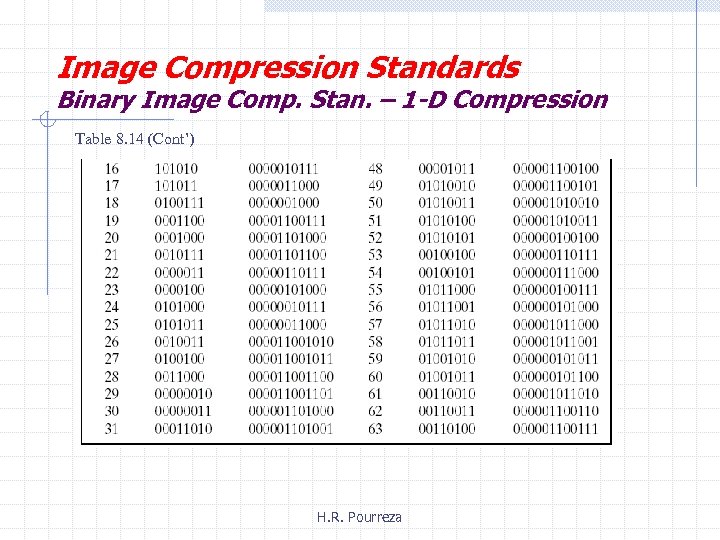
Image Compression Standards Binary Image Comp. Stan. – 1 -D Compression Table 8. 14 (Cont’) H. R. Pourreza
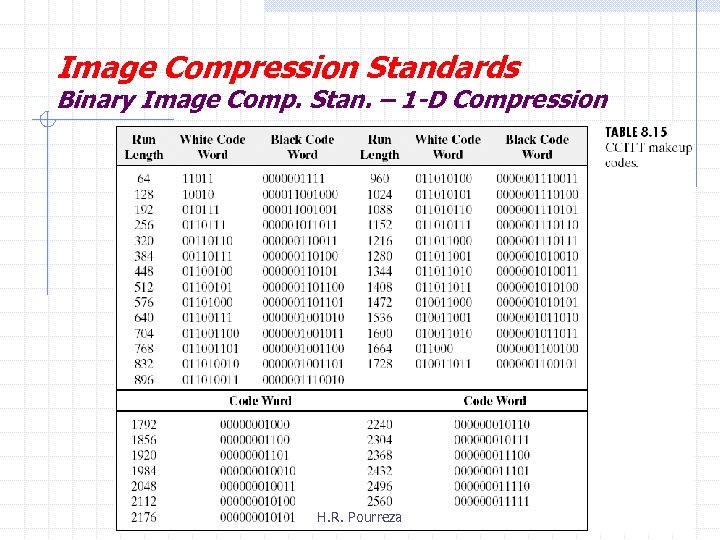
Image Compression Standards Binary Image Comp. Stan. – 1 -D Compression H. R. Pourreza

Image Compression Standards Binary Image Comp. Stan. – 2 -D Compression H. R. Pourreza

Image Compression Standards Binary Image Comp. Stan. – 2 -D Compression H. R. Pourreza

Image Compression Standards Binary Image Comp. Stan. – 2 -D Compression H. R. Pourreza

Image Compression Standards Continues Tone Still Image Comp. What Is JPEG? § "Joint Photographic Expert Group". Voted as international standard in 1992. § Works with color and grayscale images, e. g. , satellite, medical, . . . § Lossy and lossless H. R. Pourreza

Image Compression Standards Continues Tone Still Image Comp. - JPEG § First generation JPEG uses DCT+Run length Huffman entropy coding. § Second generation JPEG (JPEG 2000) uses wavelet transform + bit plane coding + Arithmetic entropy coding. H. R. Pourreza

Image Compression Standards Continues Tone Still Image Comp. - JPEG § Still-image compression standard § Has 3 lossless modes and 1 lossy mode § sequential baseline encoding § encode in one scan § input & output data precision is limited to 8 bits, while quantized DCT values are restricted to 11 bits § progressive encoding § hierarchical encoding § lossless encoding § Can achieve compression ratios of up-to 20 to 1 without noticeable reduction in image quality

Image Compression Standards Continues Tone Still Image Comp. - JPEG § Work well for continuous tone images, but not good for cartoons or computer generated images § Tend to filter out high frequency data § Can specify a quality level (Q) § with too low Q, resulting images may contain blocky, contouring and ringing structures. § 5 steps of sequential baseline encoding § § § transform image to luminance/chrominance space (YCb. Cr) reduce the color components (optional) partition image into 8 x 8 pixel blocks and perform DCT on each block quantize resulting DCT coefficients variable length code the quantized coefficients

Image Compression Standards JPEG Encoding § step 1 § § separate luminance and chrominance because more information can be removed from chrominance. human eye tends to perceive small changes in brightness better than in color § step 2 § Sub-sample color components by 2 horizontally and vertically

Image Compression Standards JPEG Encoding § step 3 § § convert elements in a tile to signed integers by subtracting one half of gray scale (0, 0) element of DCTed block is DC and other elements are AC

Image Compression Standards JPEG Encoding § step 4 § quantize and threshold by § § § T*(u, v) = round [ T(u, v)/Z(u, v)] T(u, v) = transformed coefficient Z(u, v) = transform normalization array T*(u, v) = thresholded & quantized approximation of T(u, v) when Z(u, v) = c,

Image Compression Standards JPEG Encoding § at a receiver site, T*(u, v) must be multiplied by Z(u, v) and then inverse transformed to get approximate of subimage § T**(u, v) = T*(u, v)x. Z(u, v) § normalization matrix is determined by quality level Q § if Z(u, v) > 2 T(u, v), then T*(u, v)=0 transform coefficient is completely truncated or discarded § when T*(u, v) is represented with variable length code whose length increases as |T(u, v)| increases, the number of bits is controlled by Z(u, v) § reorder quantized coefficients using zigzag pattern to form 1 -dim sequence of quantized coefficients § zigzag pattern may result in long run of zeros

Image Compression Standards JPEG Encoding § step 5 § § § DC coefficient is difference coded relative to DC coefficient of previous sub-image AC coefficients are broken into runs of zeros ending in a nonzero number. Each broken block is to be variable length coded classify each coefficient into some categories based on its range nun length and category specifies basecode and the number of bits of a code determine taling bits of a code considering least significant bits of coefficient § apply one’s complement to specify sign of the coefficient
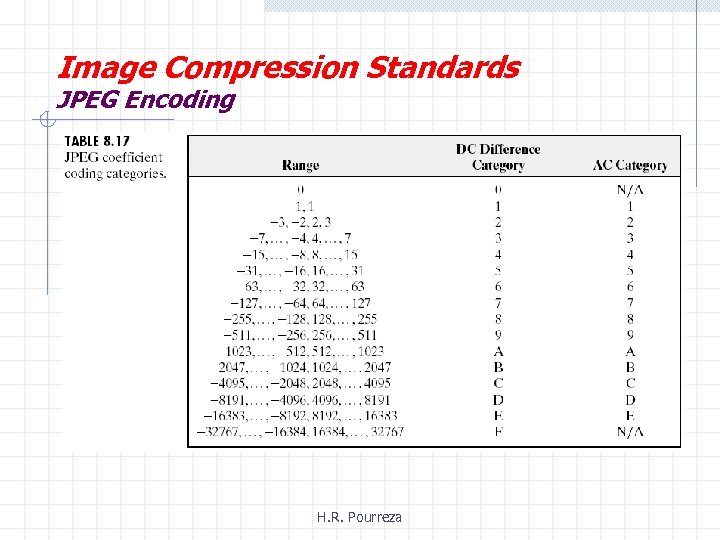
Image Compression Standards JPEG Encoding H. R. Pourreza
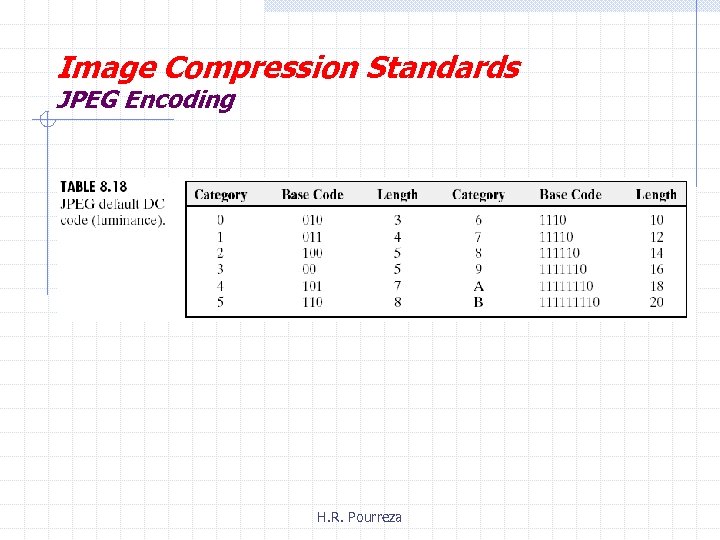
Image Compression Standards JPEG Encoding H. R. Pourreza
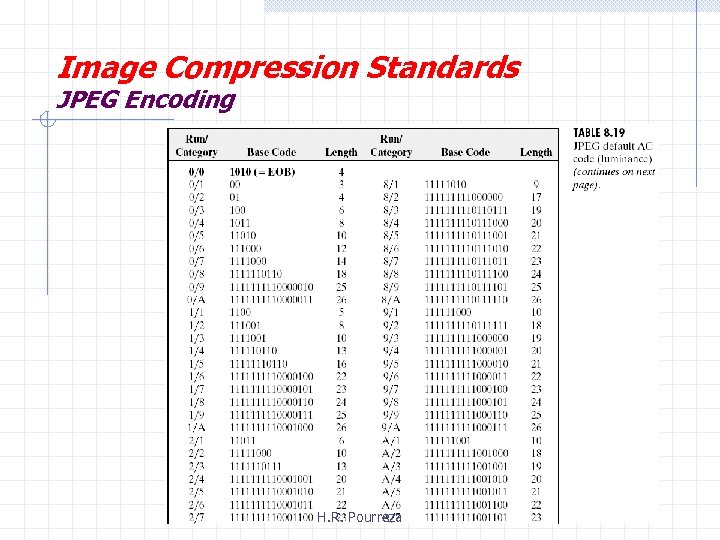
Image Compression Standards JPEG Encoding H. R. Pourreza

Image Compression Standards JPEG Encoding Table 8. 19 (Con’t) H. R. Pourreza

Image Compression Standards JPEG Encoding Original JPEG 27: 1
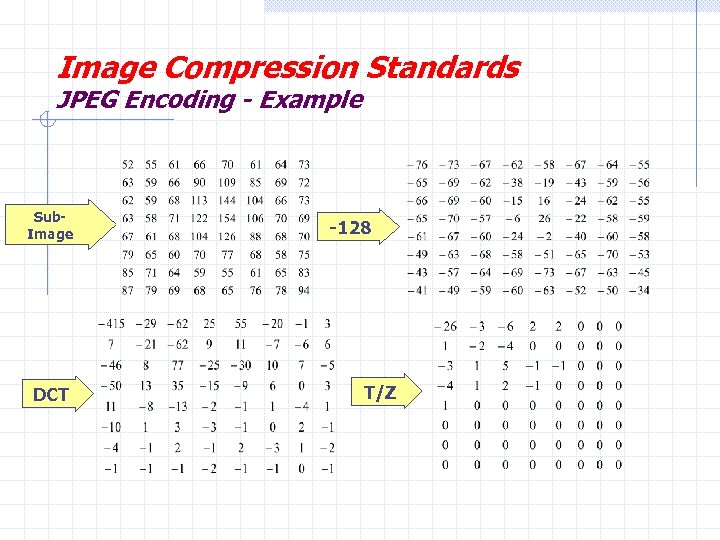
Image Compression Standards JPEG Encoding - Example Sub. Image DCT -128 T/Z

Image Compression Standards JPEG Encoding - Example Zigzag ordering [-26 -3 1 -3 -2 -6 2 -4 1 1 5 0 2 0 0 -1 2 0 0 0 -1 -1 EOB] If DC coefficient of the transformed and quantized sub-image to its immediate left was -17, the resulting DPCM: [-26 -(-17)]=-9 Category: 4 101 0110 (0111 -1) Length: 7

Image Compression Standards JPEG Encoding - Example [-26 -3 1 -3 -2 -6 2 -4 1 1 5 0 2 0 0 -1 2 0 0 0 -1 -1 EOB] 10010110 0100 001 0100 0101 100001 0110 100011 001 001 100101 11100110 110110 11110100 000 1010

Image Compression Standards JPEG Decoding - Example T*Z DCT-1 +128
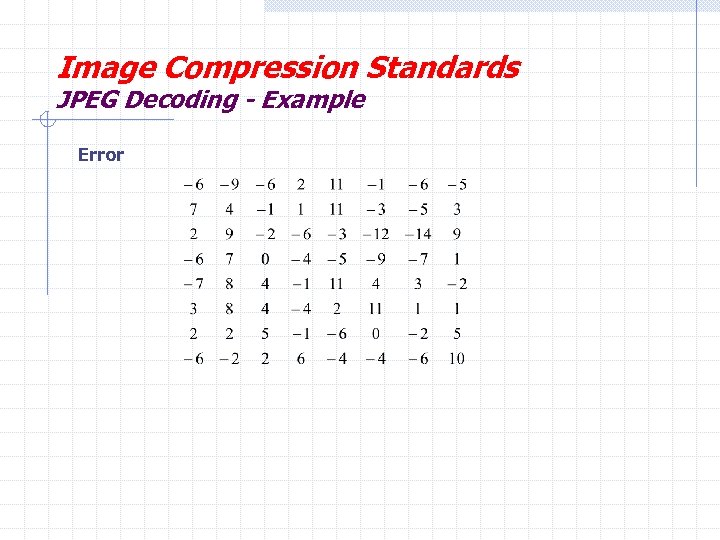
Image Compression Standards JPEG Decoding - Example Error

Image Compression Standards Video compression standards: 1. Video teleconferencing standards § § H. 261 (Px 64) H. 262 H. 263 (10 to 30 kbit/s) H. 320 (ISDN bandwidth) 2. Multimedia standards § § § MPEG-1 (1. 5 Mbit/s) MPEG-2 (2 -10 Mbit/s) MPEG-4 (5 to 64 kbit/s for mobile and PSTN and uo to 4 Mbit/s for TV and film application) H. R. Pourreza

Image Compression Standards MPEG What Is MPEG ? § "Motion Picture Expert Group", established in 1990 to create standard for delivery of audio and video. § MPEG-1 : target VHS quality on a CD-ROM (320 x 240 + CD audio @ 1. 5 Mbits/sec). H. R. Pourreza

Image Compression Standards MPEG (Interframe Coding) § Temporal DPCM is used to remove temporal redundancy first. § The motion compensated error is coded with DCT+Run length Huffman entropy coding. H. R. Pourreza

Image Compression Standards MPEG § Temporal redundancy § Prediction along the motion trajectories (motion compensation prediction) Motion Estimation § The accuracy of motion estimation has a big influence on coding efficiency. § Motion estimation is a very time-consuming work. § Some fast algorithms are needed. H. R. Pourreza
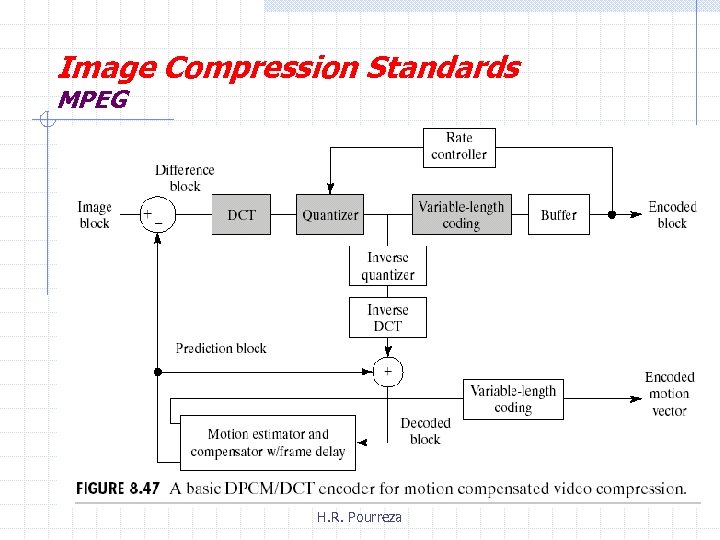
Image Compression Standards MPEG H. R. Pourreza
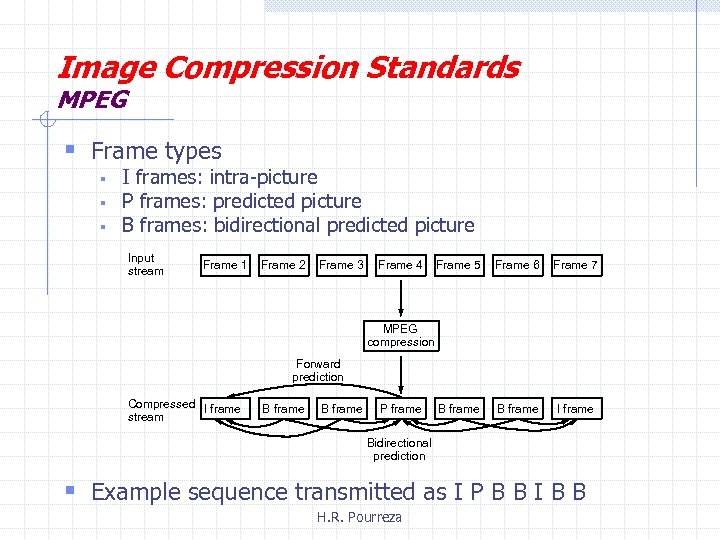
Image Compression Standards MPEG § Frame types § § § I frames: intra-picture P frames: predicted picture B frames: bidirectional predicted picture Input stream Frame 1 Frame 2 Frame 3 Frame 4 Frame 5 Frame 6 Frame 7 B frame I frame MPEG compression Forward prediction Compressed I frame stream B frame P frame Bidirectional prediction § Example sequence transmitted as I P B B I B B H. R. Pourreza
2f8c159cd5ca5f1d7e6a727f80dea75e.ppt