橢圓曲線密碼技術交通大學資訊程系陳榮傑 http www cs

橢圓曲線密碼技術交通大學資訊程系陳榮傑 http: //www. cs. nctu. edu. tw/~rjchen/ECC 2009/

Outline n n n n n [1] Discrete Logarithm Problem [2] Algorithms for Discrete Logarithm [3] Cryptosystems Based on DLP [4] Elliptic Curves [5] Elliptic Curve DLP [6] Signature Scheme: ECDSA [7] How to find secure ECs? [8] Hyperelliptic Curves [9] ID-based Cryptosystems [10] Pairing-based Cryptography p 2.

[1] Discrete Logarithm Problem n Let G is a finite cyclic group of size n generated by generator g, i. e. G = <g> = {g i | i = 1, 2, …, n} or {g i | i = 0, 1, …, n-1} i n Given g and i, it is easy to compute g by repeated squaring n Discrete logarithm problem Given , find x such that We denote p 3.

n Example 1 G = Z 19*= { 1, 2, …, 18} n=18, generator g = 2 then log 214 = 7 log 26 = 14 p 4.

n Example 2 G=GF*(23) with irreducible poly. p(x)=x 3+x+1 G=Zn*/p(x)={ 1, x, x 2, 1+x 2, x+x 2, 1+ x+x 2 } n=7, generator g = x then logx(x+1) = 3 logx(x 2+x+1) = 5 logx(x 2+1) = 6 p 5.

n Example 3 Let p =1053546280395016975304616582933958731948871814925913 48934260873425871788357518586730038628773770557793738 29258737624519904504306613508596826974102562682711472 83034897563214300237166369174066615907176472549470083 113107138189921280884003892629359 n NB: p = 158(2800 + 25) + 1 and has 807 bits. n Find x in Z, such that 2 x = 3 mod p p 6.

[2] Algorithms for Discrete Logarithm n n n trivial algorithm Shanks’ algorithm (Baby-step giant-step) Pollard rho discrete log algorithm Pohlig-Hellman algorithm The index calculus method* p 7.

The index calculus method n The index calculus method (Suitable only for G=Zp*) p 8.

n Example log 59451 mod 10007=? Choose B={2, 3, 5, 7}. Of course log 55=1. Use lucky exponents 4063, 5136, and 9865 54063 mod 10007 = 42 = 2 * 3 * 7 55136 mod 10007 = 54 = 2 * 33 59865 mod 10007 = 189 = 33 * 7 And we have three congruences: log 52 + log 53 + log 57 = 4063 mod 10006 log 52 + 3 log 53 = 5136 mod 10006 3 log 53 + log 57 = 9865 mod 10006 p 9.

There happens to be a unique solution modulo 10006 log 52=6578, log 53=6190, and log 57=1301 Choose random exponent s = 7736 and try to calculate ags = 9451*57736 mod 10007 = 8400 Since 8400 = 24*3*52*7 factors over B, we obtain log 59451 = (4 log 52 + log 53 + 2 log 55 + log 57 – s) mod 10006 = (4*6578 + 6190 + 2*1 +1301 – 7736) mod 10006 = 6057 mod 10006 p 10.

Complexity of Index Calculus n n For factoring and the discrete logarithm problem in finite fields Fq* there are index calculus algorithm (implemented with Number Field Sieve technique) These have subexponential complexity O(exp(c(ln. N)1/3(lnln. N)2/3)) p 11.

[3] Cryptosystems based on DL n n n Key Distribution n Diffie-Hellman, 1976 Encryption n Massey-Omura cryptosystem, 1983 Digital Signature n El. Gamal, 1985 p 12.

Diffie-Hellman Key Exchange Algo n n n Global Public Elements n q : prime number n α: α< q and α is a primitive root of q User A Key Generation n Select private XA : XA< q XA mod q n Calculate public YA : YA= α User B Key Generation n Select private XB : XB< q XB mod q n Calculate public YB : YB= α Generation of Secret Key by User A XA mod q n K = (YB) Generation of Secret Key by User B XB mod q n K = (YA) p 13.

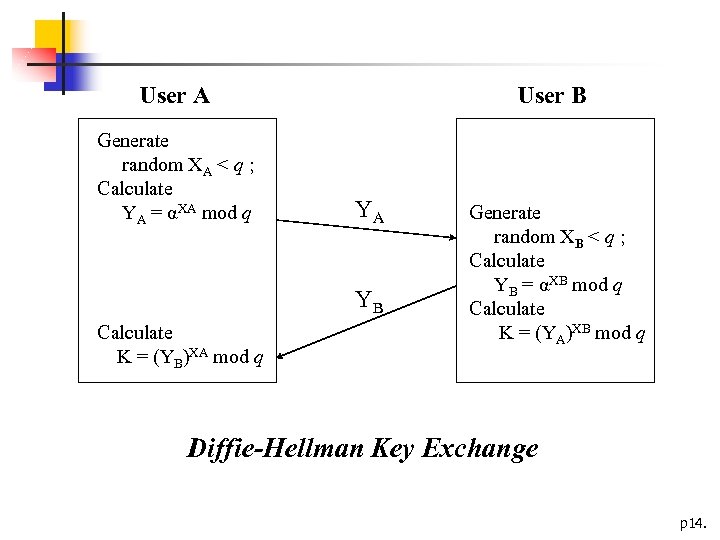
User A Generate random XA < q ; Calculate YA = αXA mod q User B YA YB Calculate K = (YB)XA mod q Generate random XB < q ; Calculate YB = αXB mod q Calculate K = (YA)XB mod q Diffie-Hellman Key Exchange p 14.

Massey-Omura for message transmission n n Parameters n q : prime number n e : a random private integer • 0 < e < q and gcd ( e, q-1) = 1 n d : an inverse of e -1 mod q-1 , i. e. , de≡ 1 mod q-1 • d = e n M : a message to be encrypted and decrypted User A wants to send a message M to User B n User A : e. A and d. A are both private n User B : e. B and d. B are both private p 15.

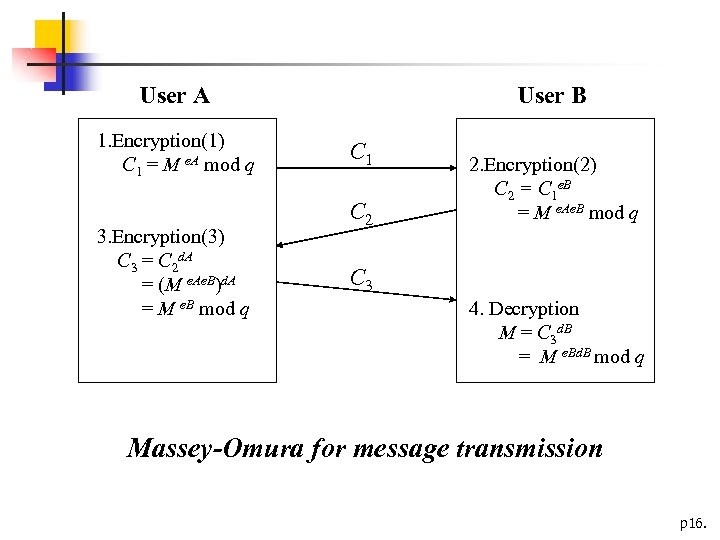
User A 1. Encryption(1) C 1 = M e. A mod q 3. Encryption(3) C 3 = C 2 d. A = (M e. Ae. B)d. A = M e. B mod q User B C 1 C 2 2. Encryption(2) C 2 = C 1 e. B = M e. Ae. B mod q C 3 4. Decryption M = C 3 d. B = M e. Bd. B mod q Massey-Omura for message transmission p 16.

El. Gamal signature scheme n n 1985 El. Gamal Parameters n p : a large prime n α: a primitive number in GF(p) n x : a private key, x [1, p-1] n y : a public key , y = αx (mod p) n m : a message to be signed , m [1, p-1] n k : a random integer that is privately selected, k [0, p-2] Signature n r = αk mod p n m = ks + rx mod φ(p) , where GCD( k, φ(p) ) = 1 n ( m , (r, s) ) is sent to the verifier Verification m = rs yr mod p n α n The signature (r, s) is accepted when the equality holds true. p 17.

El. Gamal encryption scheme n n n Parameters n p : a large prime n α: a primitive number in GF(p) n a : a private key, a [1, p-1] a n β : a public key , β = α (mod p) n m : a message to be signed , m [1, p-1] n k : a random integer that is privately selected, k [0, p-2] n K = (p, α, a, β) : public key + private key Encryption e. K(m, k)=(y 1, y 2) where y 1 = αk mod p and y 2=mβk mod p Decryption m = d. K(y 1, y 2) = y 2(y 1 a)-1 mod p p 18.

[4] Elliptic Curves n Over Fields of Characteristic p>3 n n Curve form E: Y 2 = X 3 + a. X + b where a, b Fq, q = pn 4 a 3+27 b 2≠ 0 Group operation given P 1(x 1, y 1) and P 2(x 2, y 2) compute P 3(x 3, y 3) = P 1+P 2 (x. P+Q, y. P+Q ) Q P P+Q (x. P+Q, y. P+Q) p 19.

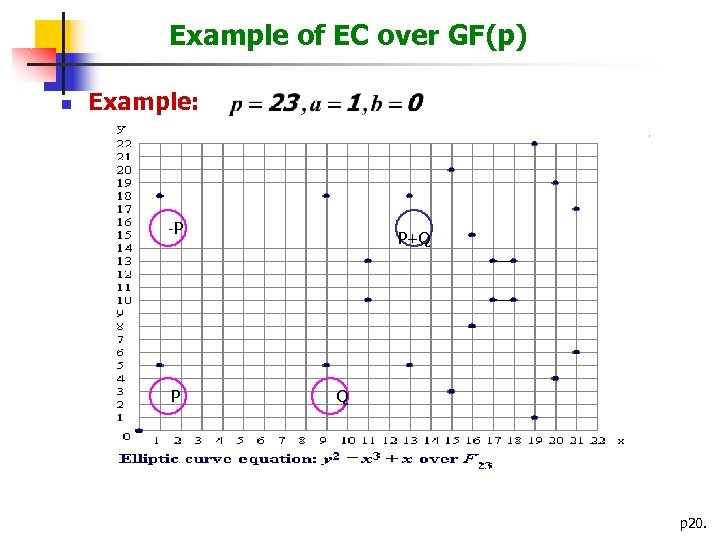
Example of EC over GF(p) n Example: -P P P+Q Q p 20.

n Addition (P 1 P 2) Computational Cost I+3 M n Doubling (P 1=P 2) Computational Cost I+4 M p 21.

n Over Fields of Characteristic 2 n n Curve form E: Y 2 + XY = X 3 + a. X 2 + b where a, b Fq, b≠ 0, q = 2 n Group operation given P 1(x 1, y 1) and P 2(x 2, y 2) compute P 3(x 3, y 3) = P 1+P 2 p 22.

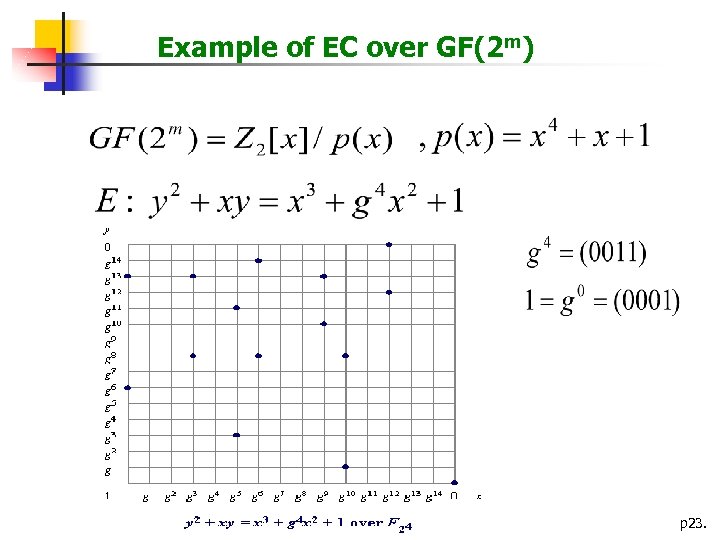
Example of EC over GF(2 m) p 23.

Addition (P 1 P 2) Computational Cost I+2 M+S Doubling (P 1=P 2) Computational Cost I+2 M+S p 24.

[5] Elliptic Curve DLP n Basic computation of ECC n n Q = k. P = where P is a curve point, k is an integer Strength of ECC n Given curve, the point P, and k. P It is hard to recover k - Elliptic Curve Discrete Logarithm Problem (ECDLP) p 25.

Security of ECC versus RSA/El. Gamal n Elliptic curve cryptosystems give the most security per bit of any known public-key scheme. n The ECDLP problem appears to be much more difficult than the integer factorisation problem and the discrete logarithm problem of Zp. (no index calculus algo!) n The strength of elliptic curve cryptosystems grows much faster with the key size increases than does the strength of RSA. p 26.

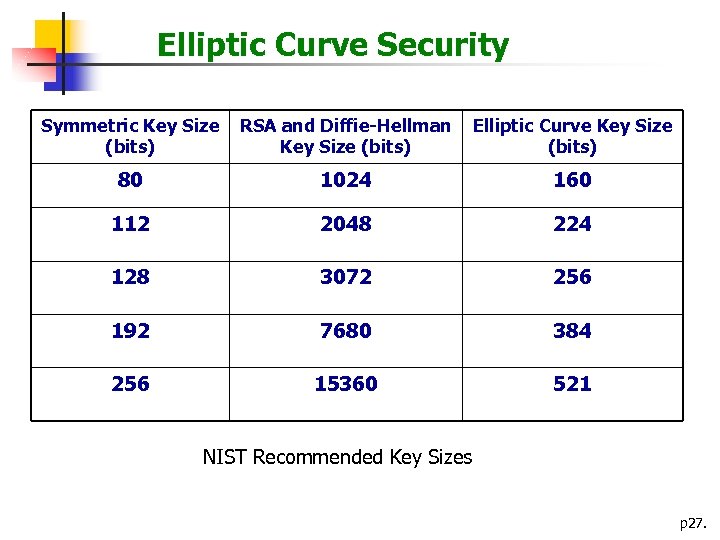
Elliptic Curve Security Symmetric Key Size (bits) RSA and Diffie-Hellman Key Size (bits) Elliptic Curve Key Size (bits) 80 1024 160 112 2048 224 128 3072 256 192 7680 384 256 15360 521 NIST Recommended Key Sizes p 27.

ECC Benefits ECC is particularly beneficial for application where: n n n computational power is limited (wireless devices, PC cards) integrated circuit space is limited (wireless devices, PC cards) high speed is required. intensive use of signing, verifying or authenticating is required. signed messages are required to be stored or transmitted (especially for short messages). bandwidth is limited (wireless communications and some computer networks). p 28.

[6] Signature Scheme: ECDSA n Digital Signature Algorithm (DSA) n n n Proposed in 1991 Was adopted as a standard on December 1, 1994 Elliptic Curve DSA (ECDSA) n FIPS 186 -2 in 2000 p 29.

Digital Signature Algorithm (DSA) L=0 mod 64, 512≤L≤ 1024 n Let p be a L-bit prime such that the DL problem in Zp* is intractable, and let q be a 160 -bit prime that divides p-1. Let α be a qth root of 1 modulo p. Define K={ (p, q, α, a, β): β=αa mod p } p, q, α, β are the public key, a is private p 30.

n n For a (secret) random number k, define sig (x, k)=(γ, δ), where γ=(αk mod p) mod q and δ=(SHA-1(x)+aγ)k-1 mod q For a message (x, (γ, δ)), verification is done by performing the following computations: e 1=SHA-1(x)*δ-1 mod q e 2=γ*δ-1 mod q ver(x, (γ, δ))=true iff. (αe 1βe 2 mod p) mod q=γ p 31.

Elliptic Curve DSA n Let p be a prime, and let E be an elliptic curve defined over Fp. Let A be a point on E having prime order q, such that DL problem in <A> is infeasible. Define K={ (p, q, E, A, m, B): B=m. A } p, q, E, A, B are the public key, m is private p 32.

n For a (secret) random number k, define sigk(x, k)=(r, s), where k. A=(u, v), r=u mod q and s=k-1(SHA-1(x)+mr) mod q n For a message (x, (r, s)), verification is done by performing the following computations: i=SHA-1(x)*s-1 mod q j=r*s-1 mod q (u, v)=i. A+j. B ver(x, (r, s))=true if and only if u mod q=r p 33.

[7] How to find secure elliptic curves ? (1) Randomly choose a, b, p and calculate #Elliptic curve (y 2=x 3+ax+b) until #E = a prime q, where #E is calculate by using Schoof-Elkies. Atkin algorithm (2) (Complex multiplication method) Given a big prime q, find p, a, b such that #Elliptic curve (y 2=x 3+ax+b) = q p 34.

[8] Hyperelliptic Curves 1. Definition of HC 2. Example of HC (rational points of HC do not form a group) 3. Divisor 4. Jacobian (Jacobian is a group) 5. HCDLP p 35.

Definitions of hyperelliptic curves n A hyperelliptic curve C of genus g over a finite field K (g≧ 1) C : y 2 + h(x)y = f(x) where n n n h(x) ∈ K[x] is a polynomial of degree at most g, f(x) ∈ K[x] is a monic polynomial of degree 2 g+1. Elliptic curves are hyperelliptic curves of genus 1. p 36.

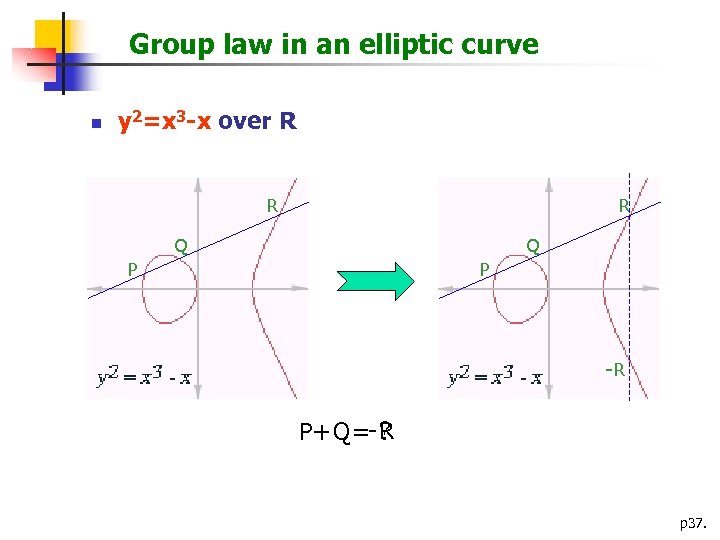
Group law in an elliptic curve n y 2=x 3 -x over R R R Q Q P P -R ？ P+Q=-R p 37.

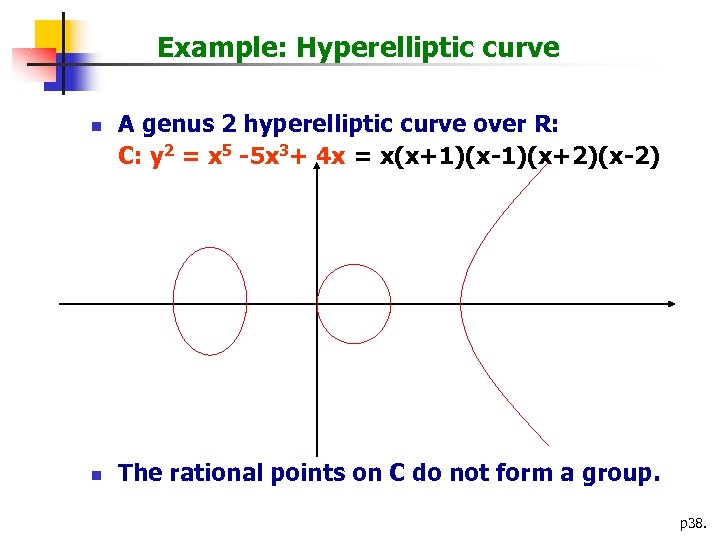
Example: Hyperelliptic curve n n A genus 2 hyperelliptic curve over R: C: y 2 = x 5 -5 x 3+ 4 x = x(x+1)(x-1)(x+2)(x-2) The rational points on C do not form a group. p 38.

Divisors n Definition : (divisor, degree) n A divisor D is a formal sum of points in C: D 1=2 P 1+P 2 -3∞ D 2= P 1+P 3 n n The degree of D, deg(D 1) =2+1 -3=0 deg(D 2) =1+1=2 The set of all divisors, denoted D, forms an additive group under the addition rule: D 1+D 2 =3 P 1+P 2+P 3 -3∞ n D 0(K) is the subgroup of all divisors defined over K and of degree 0. p 39.

Principal divisor C: y 2 = x 5 -5 x 3+ 4 x n Definition : (principal divisors) n • Let R ∈K(C) be a rational function. • x-1 The divisor of R is called a principal divisor : Q 1=(1, 0) on C div(x-1) = 2 Q 1 -2∞ n n In fact, degree of a principal divisor is 0. The set of all principal divisors, denoted P(K), is a subgroup of D 0(K). p 40.

Jacobian n Definition: (Jacobian) n The quotient group JC(K) = D 0/P is called the Jacobian of the curve C. n If D 1, D 2 ∈ D 0 and D 1 -D 2 ∈ P, then D 1 and D 2 are said to be equivalent divisors; we write D 1~D 2. p 41.

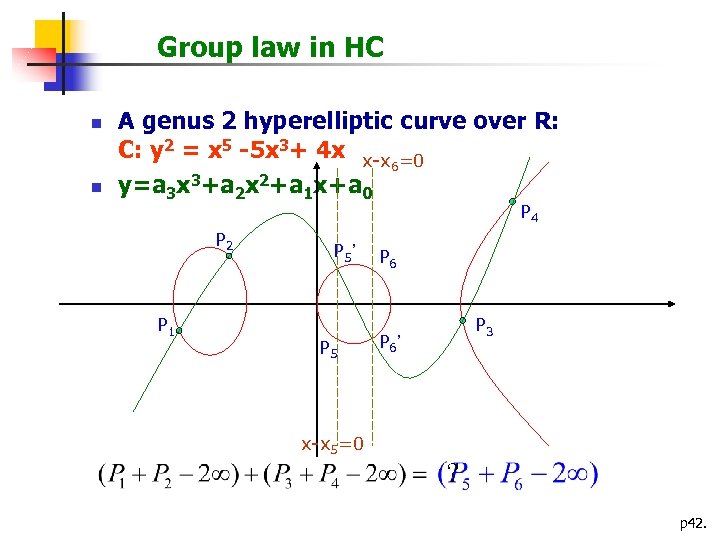
Group law in HC n n A genus 2 hyperelliptic curve over R: C: y 2 = x 5 -5 x 3+ 4 x x-x =0 6 y=a 3 x 3+a 2 x 2+a 1 x+a 0 P 4 P 2 P 1 P 5’ P 5 P 6 P 3 P 6’ x-x 5=0 ？ p 42.

HCDLP n HCDLP: (hyperelliptic curve discrete logarithm problem) n Let a divisor D 1 in JC(Fq) with known order N, and D 2 in <D 1> n To find an integer λ s. t. D 2 = λD 1 is hard. p 43.

[9] ID-based Cryptosystem IDBob is arbitrary and meaningful ex: Bob@hotmail. com or 0912345678 Setup generate params and master key Private Key Generator (PKG) Extract generate KRIDBob by IDBob and master key KRIDBob Alice (params, IDBob) Encrypt Authentication (IDBob) Bob KRIDBob Decrypt or or Verify Sign p 44.

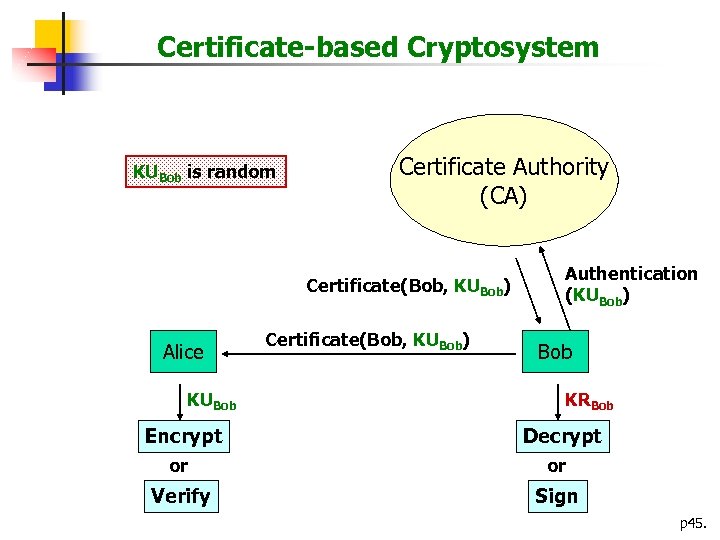
Certificate-based Cryptosystem KUBob is random Certificate Authority (CA) Certificate(Bob, KUBob) Alice KUBob Encrypt Certificate(Bob, KUBob) Authentication (KUBob) Bob KRBob Decrypt or or Verify Sign p 45.

ID-based Encryption Scheme n Proposed by Boneh and Franklin (Crypto 2001) n n First complete and efficient scheme Bilinear Pairing G 1: additive group generated by P, ord(P)=q G 2: multiplicative group with same order q Assume that DLP in G 1 and G 2 are hard Let e: G 1 x. G 1 G 2 satisfies: 1. Bilinear: e(P 1+P 2, Q)=e(P 1, Q)e(P 2, Q) e(P, Q 1+Q 2)=e(P, Q 1)e(P, Q 2) 2. Non-degenerate: P, Q G 1, s. t e(P, Q) 1 3. Computability n Bilinear Diffie-Hellman (BDH) Assumption Given P, a. P, b. P, c. P G 1 , compute e(P, P)abc is HARD! p 46.

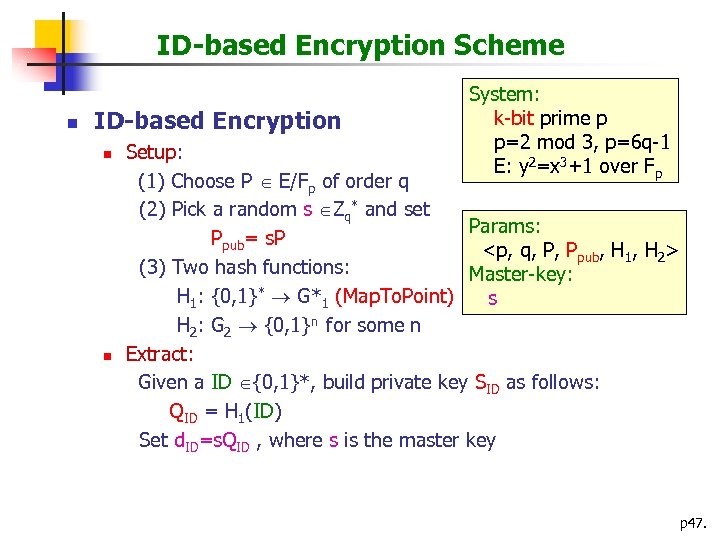
ID-based Encryption Scheme n ID-based Encryption n n System: k-bit prime p p=2 mod 3, p=6 q-1 E: y 2=x 3+1 over Fp Setup: (1) Choose P E/Fp of order q (2) Pick a random s Zq* and set Params: Ppub= s. P <p, q, P, Ppub, H 1, H 2> (3) Two hash functions: Master-key: H 1: {0, 1}* G*1 (Map. To. Point) s H 2: G 2 {0, 1}n for some n Extract: Given a ID {0, 1}*, build private key SID as follows: QID = H 1(ID) Set d. ID=s. QID , where s is the master key p 47.

ID-based Encryption Scheme d. ID=s. QID n n Encrypt: Ppub=s. P Use Map. To. Point to map ID to QID choose a random r Zq* C = < r. P, M H 2(e(QID, Ppub)r) > Decrypt: Let C=< U, V > , if U is not a point of order q then reject M = V H 2(e(d. ID, U)) e(d. ID, U)= e(s. QID, r. P)= e(QID, P)sr= e(QID, s. P)r= e(QID, Ppub)r p 48.

Weil Pairing n (Def) Weil pairing where is called the m-torsion group, Um is the group of the mth roots of unity 0 such that n Given P, Q E [m], DP, DQ Div DP ~ (P) – (O) and DQ ~ (Q) – (O). Also, f. P , f. Q such that div (f. P) = m DP and div (f. Q) = m DQ. Suppose supp (DP) supp (DQ) = Then p 49.

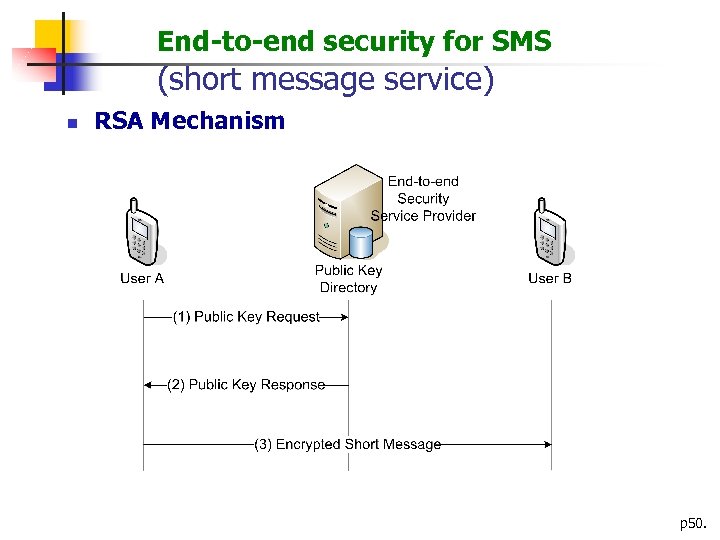
End-to-end security for SMS (short message service) n RSA Mechanism p 50.

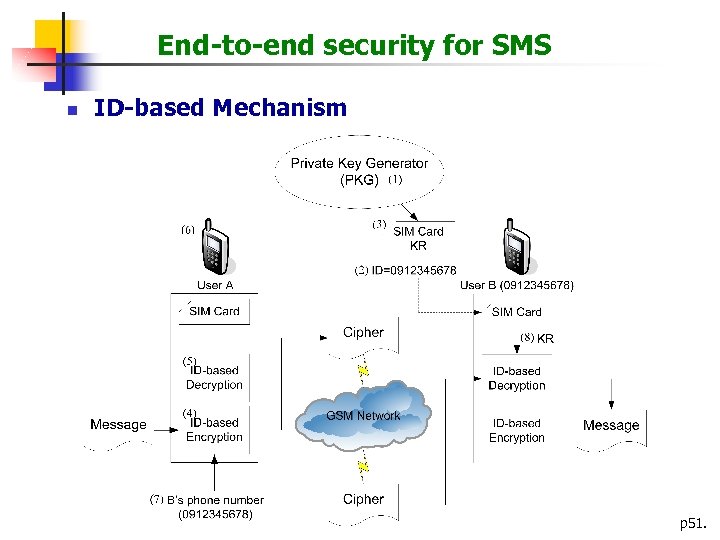
End-to-end security for SMS n ID-based Mechanism p 51.

[10] Pairing-based Cryptography 1. Implementation of Pairings Bilinear paring e: G 1 x G 2 GT G 1, G 2 : prime-order subgroups of an elliptic curve E over GF(qk) GT : prime-order subgroup of GF(qk)* k is the embedding degree of E (w. r. t. r=#E(GF(q))) k is the smallest positive integer s. t. r | qk - 1 p 52.

Various pairings: Weil pairing Tate pairing Eta pairing Ate pairing Generalized Ate pairing p 53.

2. Use of parings in cryptography Attack on ECDLP (MOV attack) One-round 3 -way key exchange (Joux) IDE (Boneh-Franklin) Short digital signature (Boneh-Lynn-Shacham) Other applications: Group signatures, Bach signatures, aggregate signatures, threshold cryptography, authenticated encryption, broadcast encryption, etc. p 54.

3. Constructing pairing-friendly curves Want k large enough so that DLP in GF(qk)* is computational infeasible, but small enough so that pairing is easy to compute. Cock-Pinch strategy MNT strategy Dupon-Enge-Morain strategy * Brezing-Weng strategy Scott-Barreto strategy p 55.

橢圓曲線密碼技術 交通大學 資訊 程系 陳榮傑 http www cs

橢圓曲線密碼技術交通大學資訊程系陳榮傑 http www cs