Zumdahl s Chapter 20 Transition Metals Chapter Contents

Zumdahl’s Chapter 20 Transition Metals

Chapter Contents ® e– configuration ® Oxidation #s & IP ® Coordination Compounds Coordination # ® Ligands ® Nomenclature ® ® Isomerism Structural Isomerism ® Stereoisomerism ® ® Bonding in Complex Ions ® Crystal Field Theory ® ® Octahedral Tetrahedral

Electronic Configurations ®d – block transition metals ® ns 2 (n– 1)d X where n = 4, 5, 6, 7 ® Potential for high spin (Hund’s Rule) ® Ions lose s electrons first. ®f – block transition elements ® ns 2 (n– 1)d 0, 1 (n– 2)f X where n = 6, 7 ® Lanthanides & Actinides are even more similar than members of d – block.

Oxidation States ® Often lose e– to Rare Gas configuration. Sc Ti V Cr Mn 3 2, 3 1, 2, 3 4 4, 5 3, 4, 4, 5, 6 7 1, 2, 3, Fe Co 2, 3, 1, 2, 3, 4, 5, 6 4 Ni Cu Zn 1, 2 2 3, 4 ® But beyond Mn, transition metal ions do not achieve that high. ® Because the 8 th IP is prohibitively expensive!

Coordination Compounds ® Often ® But neutrals possible if ligands exactly balance metal ion’s charge. ® Often ® highly colored Since MO energy separations match visible light photon energies, absorb visible light. ® Often ® complex ions (both cat– and an–) paramagnetic Duhh! These are transition metals, no? ® Dative bonded by e– donating ligands.

Coordination Number ® The But to only one of many solvent water molecules. number of ligand bonds ® Usually 6 (octahedral) but as few as 2 (linear) and as many as 8 (prismatic or antiprismatic cube). Here’s Gd bonding to a ligand called DOTA 6 ways … For a bizarre 7 coordination.

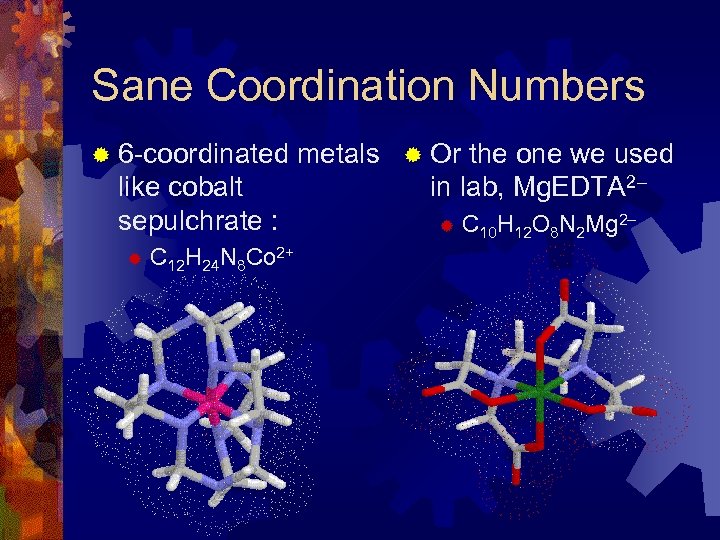Sane Coordination Numbers ® 6 -coordinated like cobalt sepulchrate : ® C 12 H 24 N 8 Co 2+ metals ® Or the one we used in lab, Mg. EDTA 2– ® C 10 H 12 O 8 N 2 Mg 2–

Ligands ® From Latin ligare, “to bind” ® Must be a Lewis base (e– donor) ® Could, as does EDTA, have several Lewis base functionalities: polydentate! ® If monodentate, should be small enough to permit others to bind. ® Relative bonding strengths: ® X– < OH– < H 2 O < NH 3 < en < NO 2– < CN– halides ethylene diamine

Naming Anionic Names ® Anions that electrically balance cationic coordination complexes can also be present as ligands in that complex! ® So they need different names that identify when they’re being used as ligands: Species Cl– As ion: chloride As ligand: chloro NO 2– CN– nitrite cyanide nitro cyano

Naming Neutral Names ® But ligands needn’t be anions; many neutral molecules are Lewis bases. ® And they too get new names appearing as ligands in coordination complexes: Species H 2 O NH 3 CO Normal: water ammonia As ligand: aqua ammine carbon monoxide carbonyl

Name That Complex, Oedipus ®[ Cr Br 2 (en)2 ] Br ® Anion, bromide, is named last (no surprise) ® chromium(III) is named next-to-last ® Ligands named 1 st in alphabetical order: Number of a ligands is shown as Greek prefix: l dibromo … ® Unless it already uses “di” then use “bis” l Dibromobis(ethylenediammine) … ® Dibromobis(ethylenediammine)chromium(III) bromide ®

Charge Overrun ® Since ligands are often anions, their charge may swamp the transition metal, leaving the complex ion negative! ® Na 2 [ Pb. I 4 ] (from Harris p. 123) ® Sodium ® ® Li tetraiodoplumbate(II) While lead(II) is the source, the Latin root is used for the complex with “ate” denoting anion. [ Ag. Cl 2 ], lithium dichloroargentate

Isomeric Complications ® dichlorobis(diethylsulfide)platinate(II) would appear to be the name of the square planar species above, but ® The square planar configuration can have another isomer where the Cl ligands are on opposite sides of the platinum, so it’s really ® cis-dichlorobis(diethylsulfide)platinate(II) ® and this is not the only way isomers arise!

Complex Isomerization Simplified ® Stereoisomers preserve bonds ® Geometric (cis-trans) isomers ® Optical (non-superimposable mirrors) ® Structural isomers preserve only atoms ® Coordination isomers swap ligands for anions to the complex. ® Linkage isomers swap lone pairs on the ligand as the bonding site.

Coordination Isomers ® Unique to coordination complexes ® [ Pb (en)2 Cl 2 ] Br 2 l bis(ethylenediammine)dichlorolead(IV) bromide ® Only 1 of 3 possible coordination isomers ® The other 2 are ® [ Pb Br (en)2 Cl ] Br Cl l ® bromobis(ethylenediammine)chlorolead(IV) l bromide chloride [ Pb Br 2 (en)2 ] Cl 2 l dibromobis(ethylenediammine)lead(IV) chloride

Optical Isomers ® We need to compare the mirror image of a sample complex to see if it can be superimposed on the original. These views of cobalt sepulchrate and its Mirror image demonstrate non-superimposition. They are optical isomers.

Colorful Complexes ® Colors we see everywhere are due, for the most part, to electronic transitions. ® Most electronic transitions, however, occur at energies well in excess of visible h. ® d-electrons transitions ought not to be visible at all, since they are degenerate. ® But, in a complex, that degeneracy is broken! Transition energies aren’t then 0.

Breaking Degeneracy ® 5 d orbitals in a tetrahedral charge field split as a doublet (E) and a triplet (T). 8 C 3 3 C 2 6 S 4 6 d h=24 Td E A 1 1 1 A 2 1 1 1 – 1 E 2 – 1 2 0 0 T 1 3 0 – 1 1 – 1 T 2 3 0 – 1 1 x 2+y 2+z 2 (2 z 2–x 2–y 2, x 2–y 2) (xy, xz, yz)

Symmetry Tells Not All ® While the symmetry tables assure us that there are now 2 energy levels for d orbitals instead of 1, we don’t know the energies themselves. ® That depends upon the field established by the ligands and the proximity of the d s. ® See Zumdahl’s Fig. 20. 26 for a visual argument why dxy, dxz, dyz are lower energy.

Other Ligand Symmetries ® Octahedral, Oh, (6 -coordinate, Fig. 20) ® Eg symmetic species for (2 z 2–x 2–y 2, x 2–y 2) ® T 2 g symmetric species for (xy, xz, yz) ® Square ® A 1 g Planar, D 4 h (Fig. 20. 27 a) symmetric species for z 2 ® B 1 g symmetric species for x 2–y 2 ® B 2 g symmetric species for xy ® Eg symmetric species for (xz, yz)

Consequences ® Degeneracies work in Hund’s favor to separate e– pairs and maximize spin. ® With high enough energy separations, , Aufbau (lowest level) wins instead. field case, large, e– pairs in lower energy states. ® Low field case, small, e– unpaired as much as feasible. ® High

Symmetry and ® tetrahedral = (4/9) octahedral (same ligands) ® As a consequence of symmetry. ® If some ligand was 9/4 as strong as the weakest to give octahedral strong field, then strong field (low-spin) tetrahedral might exist. But none does. ® Field strengths of ligands vary as: ® X– < OH– < H 2 O < NH 3 < en < NO 2– < CN–