Золотое сечение в природе и в биологии

«Золотое сечение» в природе и в биологии. Руководитель учитель математики Яровая С. П. Работу выполнила ученица 10 класса Мугу Роза.

Цель работы: • Доказать, что «золотое сечение» верх совершенства и гармонии в природе.

Что такое «Золотое сечение» ? • «Золотое сечение» уже давно стало синонимом слова «гармония» . При этом немногие понимают, что же скрывается под этими словами. Между тем, разобраться, в том, что такое «Золотое сечение» и как оно работает, достаточно просто.

Формула «Золотого сечения» • Золотое сечение – это такое деление отрезка на 2 пропорциональные части, при котором целое так относится к большей части, как большая к меньшей. • Математически эта формула выглядит так: c: b = b: a или a: b = b: c. • Итак, «Золотое сечение» – это правило пропорции, оно показывает соотношение частей и целого.

Леонардо Фибоначчи (Пизанский) • С историей золотого сечения связано имя итальянского математика монаха Леонардо Фибоначчи. Он выстроил такой ряд цифр: 0 1 1 2 3 5 8 13 2134 55 89 144 и т. д. каждый его член, начиная с третьего равен сумме двух предыдущих 2+3=5; 3+5=8; 8+5=13; 8+13=21; 13+21=34; 21+34=55 и т. д.

«Золотое сечение» не только в математике. • Живые системы также обладают свойствами, характерными для "золотого сечения". Например: пропорции тел, спиральные структуры или параметры биоритмов и др.

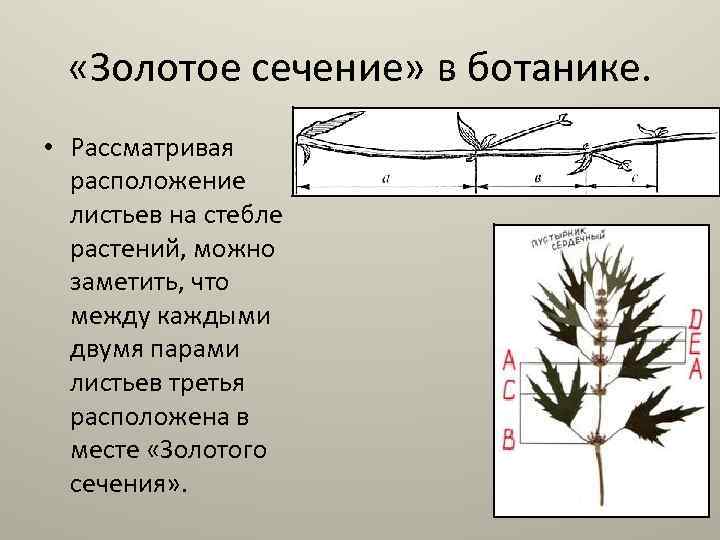
«Золотое сечение» в ботанике. • Рассматривая расположение листьев на стебле растений, можно заметить, что между каждыми двумя парами листьев третья расположена в месте «Золотого сечения» .

«Золотое сечение» у насекомых. • У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2, 3, 5, 8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

«Золотые» спирали у животных • «Золотые» спирали широко распространены в животном мире. Рога животных растут лишь с одного конца. Этот рост осуществляется по логарифмической спирали.

«Золотое сечение» в строении человеческого тела. • В разные времена и у разных народов эталоны длины частей человека были одинаковыми: они происходили от человеческого тела. • В человеке заложены пропорции, отобранные самой природой. Начало этим мерам дает рост человека. В строении черт лица человека и в руке, так же есть множество примеров, приближающихся по значению к этой формуле.

«Золотое сечение» в анатомии • Рост человека делится в «золотых» пропорциях линией пояса, а так же линией, проведённой через кончики средних пальцев опущенных рук, а нижняя линия лица – ртом.

Кости человека выдержаны в пропорции, близкой к золотому сечению. И чем ближе пропорции к формуле золотого сечения, тем более идеальным выглядит внешность человека.

• Расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1: 1. 618. • Не только эти соотношения но и многие другие пропорции лица соответствуют принципу «золотого сечения» .

• Формула золотого сечения видна при взгляде на указательный палец. Каждый палец руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца = золотое сечение (за исключением большого пальца). • Соотношение средний палец / мизинец = золотое сечение • У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения (цифры 2, 3, 5 и 8 - это и есть числа последовательности Фибоначчи). • Также следует отметить тот факт, что у большинства людей расстояние между концами расставленных рук равно росту.

«Золотые» пропорции в строении молекулы ДНК • Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой так же содержит в себе закон «золотой пропорции» . Молекула ДНК состоит из двух вертикально переплетённых между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем – одна стомиллионная доля сантиметра) • Так вот 21 и 34 – это цифры следующие друг за другом в последовательности чисел Фибоначчи, т. е. соотношение длины и ширины логарифмической спирали ДНК несет в себе формулу «Золотого сечения» 1: 1. 618

Почему же «золотая пропорция» представляется такой гармоничной? • У теории «золотого сечения» есть масса как сторонников так и противников. Вообще, идея о том, что красоту можно измерить и просчитать с помощью математической формулы, симпатична далеко не всем. И, возможно, эта концепция действительно казалась бы надуманной математической эстетикой, если бы не многочисленные примеры природного формообразования, соответствующие «золотому сечению» .

ВЫВОДЫ: • Значение «золотого сечения» в современной науке очень велико. Эта пропорция используется практически во всех областях знаний. Её пытались изучить многие учёные и гении : Аристотель Геродот, Леонардо Да Винчи, но полностью этого сделать никому не удалось. • В своей работе мы хотели продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведённые исследования показали, что многое в окружающем мире подчиняется правилу «Золотого сечения» .

Спасибо за внимание!