c4bfd11966494f30a404910cf29b178b.ppt
- Количество слайдов: 90

zimbio. com swifteconomics. com britannica. com High Performance Computing at Arizona State University Gil Speyer Arizona State University Fulton High Performance Computing January 13 th, 2010 speyer@asu. edu

What is Parallel Computing? • Parallel computing: use of multiple processors or computers working together on a common task. – Each processor works on its section of the problem – Processors can exchange information Grid of Problem to be solved y CPU #1 works on this area exchange CPU #2 works on this area of the problem exchange CPU #3 works on this area of the problem exchange CPU #4 works on this area of the problem x 2 HPC at ASU

Why Do Parallel Computing? • Limits of single CPU computing – performance – available memory • Parallel computing allows one to: – solve problems that don’t fit on a single CPU – solve problems that can’t be solved in a reasonable time • We can solve… – larger problems – faster – more cases 3 HPC at ASU

Limits of Parallel Computing • Theoretical Upper Limits – Amdahl’s Law • Practical Limits – Load balancing – Non-computational sections • Other Considerations – time to re-write code 4 HPC at ASU

Theoretical Upper Limits to Performance • All parallel programs contain: – parallel sections (we hope!) – serial sections (unfortunately) • Serial sections limit the parallel effectiveness • Amdahl’s Law states this formally 5 HPC at ASU

Amdahl’s Law • Amdahl’s Law places a strict limit on the speedup that can be realized by using multiple processors. – Effect of multiple processors on run time – Effect of multiple processors on speed up 1 = S fs + f p / N – Where • fs = serial fraction of code • fp = parallel fraction of code • N = number of processors 6 HPC at ASU

Limit cases of Amdahl’s Law • Speed up formula: S= – Where 1 fs + f p / N • fs = serial fraction of code • fp = parallel fraction of code • N = number of processors – Case: • fs = 0, fp = 1, then S = N • N goes to infinity: S = 1/fs, so if 10% of the code is sequential, you will never speed up by more than 10, no matter the number of processors. 7 HPC at ASU
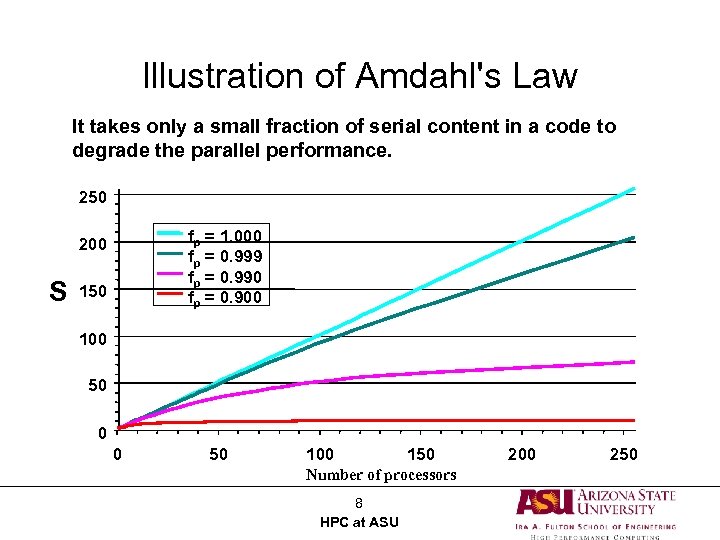
Illustration of Amdahl's Law It takes only a small fraction of serial content in a code to degrade the parallel performance. 250 fp = 1. 000 fp = 0. 999 fp = 0. 990 fp = 0. 900 200 S 150 100 50 0 0 50 100 150 Number of processors 8 HPC at ASU 200 250
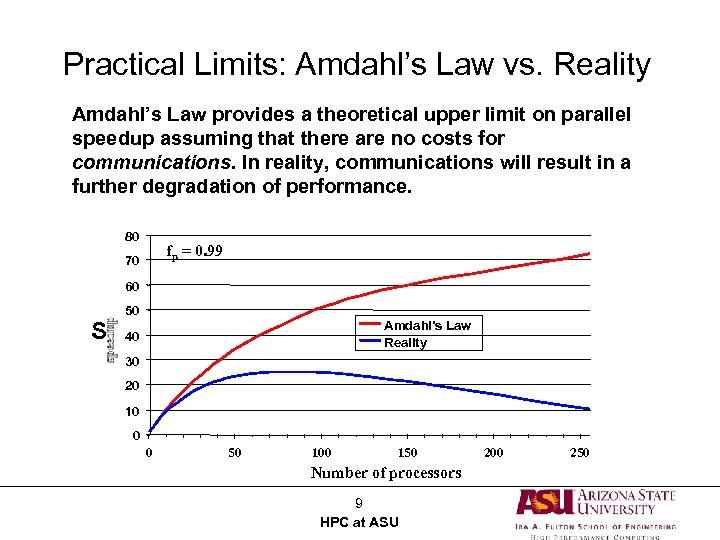
Practical Limits: Amdahl’s Law vs. Reality Amdahl’s Law provides a theoretical upper limit on parallel speedup assuming that there are no costs for communications. In reality, communications will result in a further degradation of performance. 80 fp = 0. 99 70 60 S 50 Amdahl's Law Reality 40 30 20 10 0 0 50 100 150 Number of processors 9 HPC at ASU 200 250

Practical Limits: Amdahl’s Law vs. Reality • In reality, the situation is even worse than predicted by Amdahl’s Law due to: – – Load balancing (waiting) Scheduling (shared processors or memory) Communications I/O 10 HPC at ASU

Other Considerations • Writing effective parallel applications is difficult! – Load balance is important – Communication can limit parallel efficiency – Serial time can dominate • Is it worth your time to rewrite your application? – Do the CPU requirements justify parallelization? – Will the code be used just once? 11 HPC at ASU

Types of Parallel Computers • Until recently, Flynn's taxonomy was commonly used to classify parallel computers into one of four basic types: – Single instruction, single data (SISD): single scalar processor – Single instruction, multiple data (SIMD “array processor”): Connection Machine, Mas. Par – Multiple instruction, single data (MISD): various special purpose machines – Multiple instruction, multiple data (MIMD): Nearly all parallel machines these days 12 HPC at ASU

Types of Parallel Computers • However, since the MIMD model “won, ” a much more useful way to classify modern parallel computers is by their memory model – shared memory – distributed memory 13 HPC at ASU
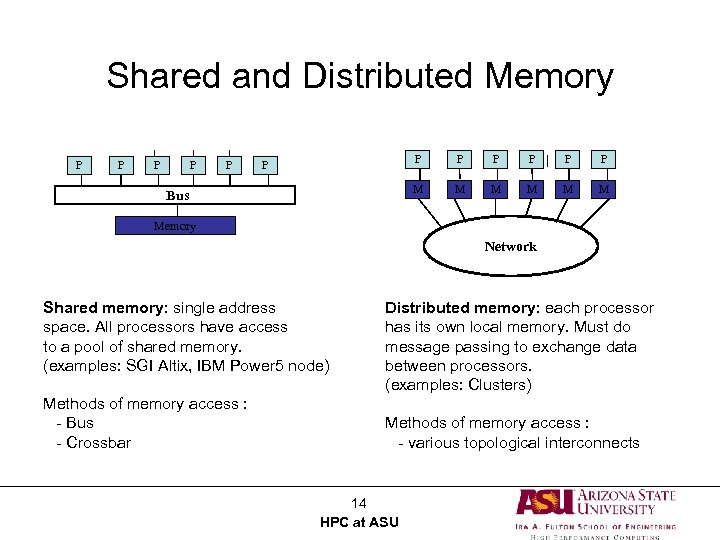
Shared and Distributed Memory P P P B Bus US P P P M M M Memory Network Shared memory: single address space. All processors have access to a pool of shared memory. (examples: SGI Altix, IBM Power 5 node) Methods of memory access : - Bus - Crossbar Distributed memory: each processor has its own local memory. Must do message passing to exchange data between processors. (examples: Clusters) Methods of memory access : - various topological interconnects 14 HPC at ASU

Reasons for Each System • SMPs: easy to build, easy to program, good priceperformance for small numbers of processors; predictable performance due to UMA • cc-NUMAs (Distributed Shared memory machines) : enables larger number of processors and shared memory address space than SMPs while still being easy to program, but harder and more expensive to build • Distributed memory MPPs and clusters: easy to build and to scale to large numbers of processors, but hard to program and to achieve good performance • Multi-tiered/hybrid/CLUMPS: combines best (worst? ) of all worlds… but maximum scalability! 15 HPC at ASU

Programming Parallel Computers • Programming single-processor systems is (relatively) easy due to: – single thread of execution – single address space • Programming shared memory systems can benefit from the single address space • Programming distributed memory systems is the most difficult due to multiple address spaces and need to access remote data 16 HPC at ASU

Programming Parallel Computers • Both parallel systems (shared memory and distributed memory) offer ability to perform independent operations on different data (MIMD) and implement task parallelism • Both can be programmed in a data parallel, SIMD fashion 17 HPC at ASU

Types of Parallelism: Two Extremes • Data parallelism – Each processor performs the same task on different data • Task parallelism – Each processor performs a different task • Most applications fall somewhere on the continuum between these two extremes 18 HPC at ASU

Data Parallel Programming Example • One code will run on 2 CPUs • Program has array of data to be operated on by 2 CPUs so array is split into two parts. CPU A CPU B program: … if CPU=a then low_limit=1 upper_limit=50 elseif CPU=b then low_limit=51 upper_limit=100 end if do I = low_limit, upper_limit work on A(I) end do. . . end program: … low_limit=1 upper_limit=50 do I= low_limit, upper_limit work on A(I) end do … end program 19 HPC at ASU program: … low_limit=51 upper_limit=100 do I= low_limit, upper_limit work on A(I) end do … end program

Task Parallel Programming Example • One code will run on 2 CPUs • Program has 2 tasks (a and b) to be done by 2 CPUs CPU A program. f: … initialize. . . if CPU=a then do task a elseif CPU=b then do task b end if …. end program. f: … initialize … do task a … end program 20 HPC at ASU CPU B program. f: … initialize … do task b … end program

Single Program, Multiple Data (SPMD) • SPMD: dominant programming model for shared and distributed memory machines. – One source code is written – Code can have conditional execution based on which processor is executing the copy – All copies of code are started simultaneously and communicate and sync with each other periodically • MPMD: more general, and possible in hardware, but no system/programming software enables it 21 HPC at ASU
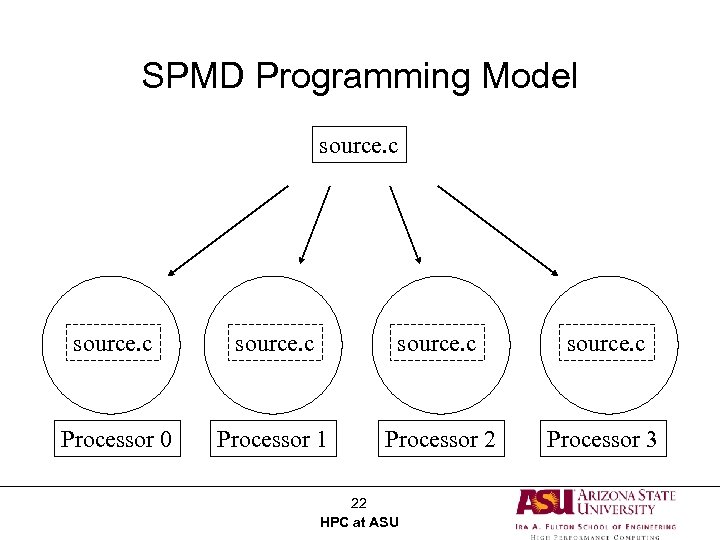
SPMD Programming Model source. c Processor 0 Processor 1 Processor 2 Processor 3 22 HPC at ASU

Shared Memory vs. Distributed Memory • Tools can be developed to make any system appear to look like a different kind of system – distributed memory systems can be programmed as if they have shared memory, and vice versa – such tools do not produce the most efficient code, but might enable portability • HOWEVER, the most natural way to program any machine is to use tools & languages that express the algorithm explicitly for the architecture. 23 HPC at ASU

Shared Memory Programming: Open. MP • Shared memory systems (SMPs, cc-NUMAs) have a single address space: – applications can be developed in which loop iterations (with no dependencies) are executed by different processors – shared memory codes are mostly data parallel, ‘SIMD’ kinds of codes – Open. MP is the new standard for shared memory programming (compiler directives) – Vendors offer native compiler directives 24 HPC at ASU
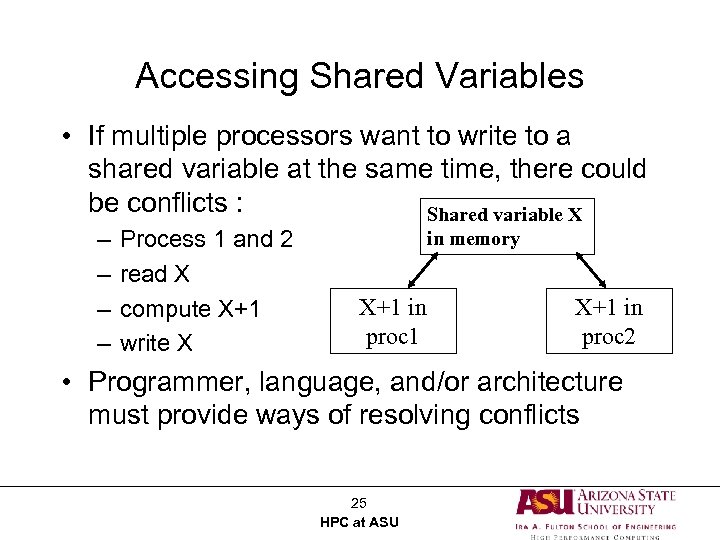
Accessing Shared Variables • If multiple processors want to write to a shared variable at the same time, there could be conflicts : Shared variable X – – Process 1 and 2 read X compute X+1 write X in memory X+1 in proc 1 X+1 in proc 2 • Programmer, language, and/or architecture must provide ways of resolving conflicts 25 HPC at ASU

Open. MP Example #1: Parallel Loop !$OMP PARALLEL DO do i=1, 128 b(i) = a(i) + c(i) end do !$OMP END PARALLEL DO • The first directive specifies that the loop immediately following should be executed in parallel. The second directive specifies the end of the parallel section (optional). • For codes that spend the majority of their time executing the content of simple loops, the PARALLEL DO directive can result in significant parallel performance. 26 HPC at ASU

Open. MP Example #2: Private Variables !$OMP PARALLEL DO SHARED(A, B, C, N) PRIVATE(I, TEMP) do I=1, N TEMP = A(I)/B(I) C(I) = TEMP + SQRT(TEMP) end do !$OMP END PARALLEL DO • In this loop, each processor needs its own private copy of the variable TEMP. If TEMP were shared, the result would be unpredictable since multiple processors would be writing to the same memory location. 27 HPC at ASU

Distributed Memory Programming: MPI • Distributed memory systems have separate address spaces for each processor – Local memory accessed faster than remote memory – Data must be manually decomposed – MPI is the standard for distributed memory programming (library of subprogram calls) – Older message passing libraries include PVM and P 4; all vendors have native libraries such as SHMEM (T 3 E) and LAPI (IBM) 28 HPC at ASU
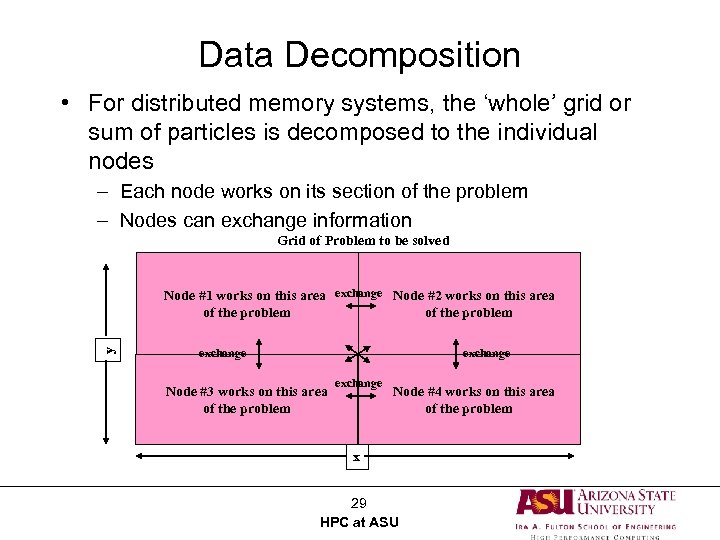
Data Decomposition • For distributed memory systems, the ‘whole’ grid or sum of particles is decomposed to the individual nodes – Each node works on its section of the problem – Nodes can exchange information Grid of Problem to be solved y Node #1 works on this area exchange Node #2 works on this area of the problem exchange Node #3 works on this area of the problem exchange Node #4 works on this area of the problem x 29 HPC at ASU

Typical Data Decomposition • Example: integrate 2 -D propagation problem: Starting partial differential equation: Finite Difference Approximation: PE #1 PE #2 PE #3 PE #4 PE #5 PE #6 PE #7 y PE #0 x 30 HPC at ASU

MPI Example #1 • Every MPI program needs these: #include <mpi. h> /* the mpi include file */ int main(int argc, char *argv[]) { /* Initialize MPI */ ierr=MPI_Init(&argc, &argv); /* How many total PEs are there */ ierr=MPI_Comm_size(MPI_COMM_WORLD, &n. PEs); /* What node am I (what is my rank? */ ierr=MPI_Comm_rank(MPI_COMM_WORLD, &iam); . . . ierr=MPI_Finalize(); } 31 HPC at ASU
![MPI Example #2 #include "mpi. h” int main(int argc, char *argv[]) int argc; char MPI Example #2 #include "mpi. h” int main(int argc, char *argv[]) int argc; char](https://present5.com/presentation/c4bfd11966494f30a404910cf29b178b/image-32.jpg)
MPI Example #2 #include "mpi. h” int main(int argc, char *argv[]) int argc; char *argv[]; { int myid, numprocs; MPI_Init(&argc, &argv); MPI_Comm_size(MPI_COMM_WORLD, &numprocs); MPI_Comm_rank(MPI_COMM_WORLD, &myid); /* print out my rank and this run's PE size*/ printf("Hello from %dn", myid, " of ", numprocs); MPI_Finalize(); } 32 HPC at ASU

MPI: Sends and Receives • Real MPI programs must send and receive data between the processors (communication) • The most basic calls in MPI (besides the initialization, rank/size, and finalization calls) are: – MPI_Send – MPI_Recv • These calls are blocking: the source processor issuing the send/receive cannot move to the next statement until the target processor issues the matching receive/send. 33 HPC at ASU

Message Passing Communication • Processes in message passing program communicate by passing messages • • A B Basic message passing primitives Send (parameters list) Receive (parameter list) Parameters depend on the library used 34 HPC at ASU

MPI Example #3: Send/Receive #include "mpi. h" /****************************** This is a simple send/receive program in MPI ******************************/ int main(argc, argv) int argc; char *argv[]; { int myid, numprocs, tag, source, destination, count, buffer ; MPI_Status status; } MPI_Init(&argc, &argv); MPI_Comm_size(MPI_COMM_WORLD, &numprocs); MPI_Comm_rank(MPI_COMM_WORLD, &myid); tag=1234; source=0; destination=1; count=1; if(myid == source){ buffer=5678; MPI_Send(&buffer, count, MPI_INT, destination, tag, MPI_COMM_WORLD); printf("processor %d sent %dn", myid, buffer); } if(myid == destination){ MPI_Recv(&buffer, count, MPI_INT, source, tag, MPI_COMM_WORLD, &status); printf("processor %d got %dn", myid, buffer); } MPI_Finalize(); 35 HPC at ASU

Programming Multi-tiered Systems • Systems with multiple shared memory nodes are becoming common for reasons of economics and engineering. • Memory is shared at the node level, distributed above that: – Applications can be written using Open. MP + MPI – Developing apps with only MPI usually possible 36 HPC at ASU

Saguaro Cluster Overview 37 HPC at ASU

Overview • Saguaro is a ~4500 processor Dell Linux cluster, – – – >40 trillion floating point operations per second >9 TB aggregate RAM >400 TB aggregate disk Infiniband Interconnect Located in GWC 167 • Saguaro is a true *cluster* architecture – Each node has 8 processors and 16 GB of RAM. – Programs needing more resources *must* use parallel programming – Normal, single processor applications *do not go faster* on Saguaro 38 HPC at ASU

star Cluster Overview Saguaro Summary Characteristics lonestar. tacc. utexas. edu Hardware Components Compute Nodes Dell 1955 336 “Harpertown” Nodes 220 “Clovertown” Nodes 200 “Nocona” Nodes A few special purpose nodes 4964 Cores total 2. 66/2. 83 GHz 8 MB/Cache 16 GB Mem/node 8 cores/node SCRATCH File System I/O Nodes Dell Filers - Data. Direct 4 I/O Nodes Lustre File System 300 TB Login and Service Nodes 2 login 3. 2 Ghz, 2 GB mem 4 service blades (scheduler, monitor, logs, allocations, etc). Interconnect (MPI) 24 -port leafs Infini. Band (Top. Spin) 144 -port cores 1 or 2 GB/sec P-2 -P Fat Tree Topology Ethernet (Gig. E) 128 MB/sec P-2 -P Fat Tree Topology 39 HPC at ASU
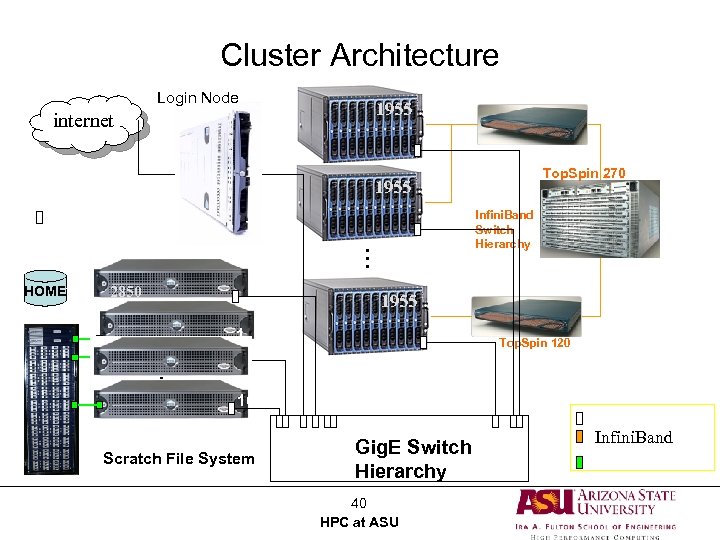
Cluster Architecture Login Node 1955 internet 1955 1 2 2850 1955 130 1 2 … HOME Infini. Band Switch Hierarchy … Raid 5 Top. Spin 270 2 Top. Spin 120 16 I/O Nodes Scratch File System Gig. E Switch Hierarchy 40 HPC at ASU Gig. E Infini. Band Fibre Channel

Compute Node Dell Power. Edge 1955 7 U 10 blades Blade: Chipset: Memory: FSB: Cache: Blade Intel® Xeon Core Technology 4 cores per blade Intel 5000 P Chipset 8 GB 2: 1 memory interleave (533 MHz DDR 2) 1333 MHz (Front Side Bus) 4 MB L 2 “Smart” Cache 41 HPC at ASU

Speeds & Feeds (Xeon/Pentium 4 ) 2 W (load) CP 1 W (load) CP 2 W (store) CP 1 W (store) CP Regs. Latencies 2 x @533 MHz FB-DIMM 2. 66 GHz CPU L 1 Data 16 KB 3 CP on die L 2 0. 39 W CP Bandwidth Shared by FOUR cores Memory 4 MB 14 -16 CP 4 FLOPS/CP Cache Line size L 1/L 2 = 8 W/8 W 42 HPC at ASU ~300 CP W DP Word (64 bit) CP Clock Period
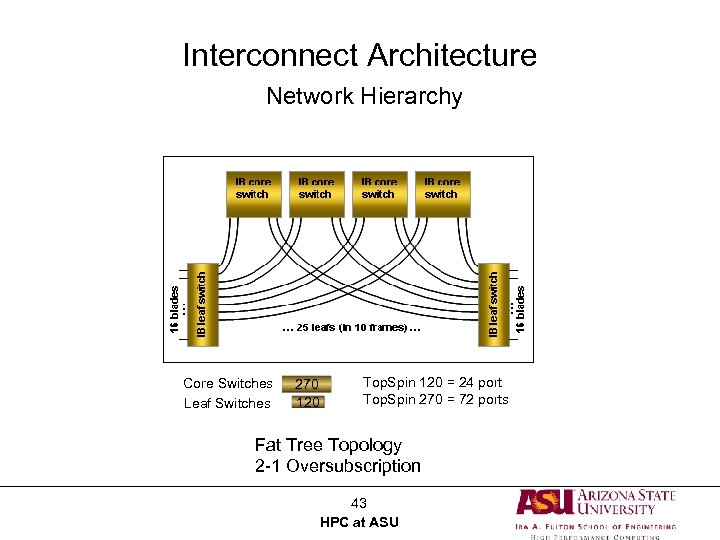
Interconnect Architecture Network Hierarchy Lonestar Infini. Band Topology Core Switches Leaf Switches 270 120 Top. Spin 120 = 24 port Top. Spin 270 = 72 ports Fat Tree Topology 2 -1 Oversubscription 43 HPC at ASU

Large Scale Parallel FDTD Simulation of Full 3 D Photonic Crystal Structures† Richard Akis, J. S. Ayubi-Moak, S. M. Goodnick, *P. Sotirelis, G. Speyer, and D. Stanzione Department of Electrical Engineering and Center for Solid State Electronics Research, Arizona State University, Tempe, AZ *High Performance Technologies, Inc. WPAFB, Dayton, OH † This work was supported by a grant from the High Performance Modernization Project (HPCMP) in collaboration with High Performance Technologies, Inc. (HPTi) 44 HPC at ASU

Outline: • Motivation • Photonic crystals • Photonic devices • The FDTD CPML Method • General formalism • Comments about the current version of ASU’s parallel FDTD simulator • Results • Demonstration of photonic band gap behavior in a 3 D photonic crystal • Defect resonances and waveguides http: //www/photonics. tfp. uni-karlsruhe. de/research. html http: //pages. ief. u-psud. fr 45 HPC at ASU
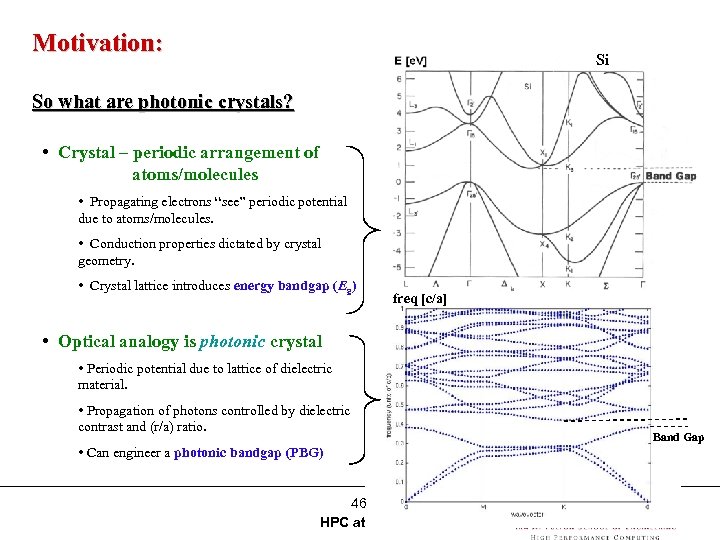
Motivation: Si So what are photonic crystals? • Crystal – periodic arrangement of atoms/molecules • Propagating electrons “see” periodic potential due to atoms/molecules. • Conduction properties dictated by crystal geometry. • Crystal lattice introduces energy bandgap (Eg) freq [c/a] • Optical analogy is photonic crystal • Periodic potential due to lattice of dielectric material. • Propagation of photons controlled by dielectric contrast and (r/a) ratio. • Can engineer a photonic bandgap (PBG) 46 HPC at ASU Band Gap

• Photonic crystals/PBM shown great deal of promise for true integrated optics. • Waveguides with small bends possible making compact integrated photonic circuits (IPCs) achievable. • Design/fabrication is challenging • Efficient simulation tools needed to realize very low loss IPCs bend splitter resonator cavity http: //www/photonics. tfp. unikarlsruhe. de/research. html http: //pages. ief. u-psud. fr 47 HPC at ASU

The Simulation Problem: • Structures employing PBG materials can be simulated using the finite difference time domain (FDTD) technique. • Typically, a given PC geometry requires many grid cells (~107 cells) to resolve even a limited number of periods. • Memory intensive computations that are virtually impossible to do on a computer with one processor • Thus, Modeling of 3 D PCB structures dictates vital need for parallel HPC architectures with optimized domain decomposition. An actual 3 D PBG crystal Minghao Qi, Elefterios Lidorikis, Peter T. Rakich, • We have developed an FDTD Steven G. Johnson, J. D. Joannopoulos, Erich P. simulator with the desired capabilities. Ippen & Henry I. Smith, “A three-dimensional optical photonic crystal with designed point defects, ” 48 Nature, vol. 429, 538, 2004. HPC at ASU

The Finite-Difference Time Domain (FDTD) Method In isotropic medium, Maxwell’s curl equations are: K. S. Yee, IEEE Trans. Antennas Propagat. , 14(302) 1966 ü ü 2 nd order accurate. ü 6 scalar PDEs Direct explicit solution of Maxwell’s equations (i. e. no matrix inversion required). Complete “full-wave” method without approximation (i. e. no pre-selection of output modes or solution form necessary. ) ü Easy to parallelize. 49 HPC at ASU

Parallel Processing -Domain Decomposition • 3 D domain decompositions have been implemented within the MPI framework of our simulator and is the default • In order to reduce the computation steps, redundant calculations at boundary regions were employed [Hanawa et al. , IEEE Trans. on Mag, 43(4), 1545 (2007)] 50 HPC at ASU The full 3 D domain is subdivided into equally sized blocks which each processor handles on its own
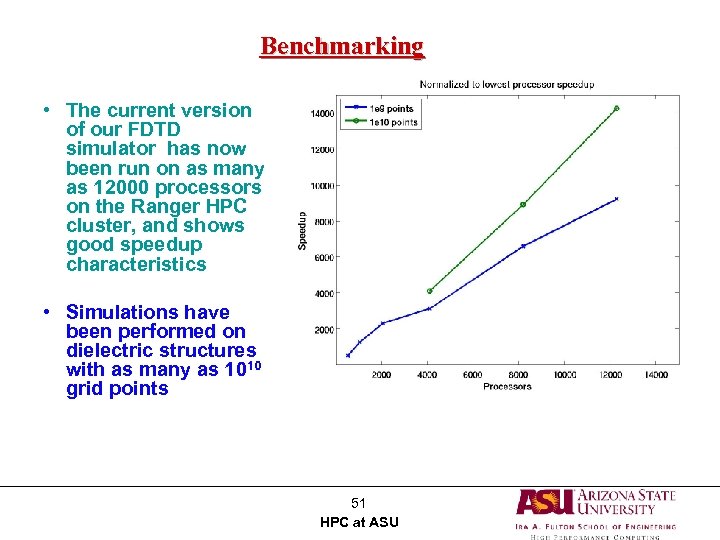
Benchmarking • The current version of our FDTD simulator has now been run on as many as 12000 processors on the Ranger HPC cluster, and shows good speedup characteristics Cross sectional slice from a simulation with 109 points • Simulations have been performed on dielectric structures with as many as 1010 grid points 51 HPC at ASU
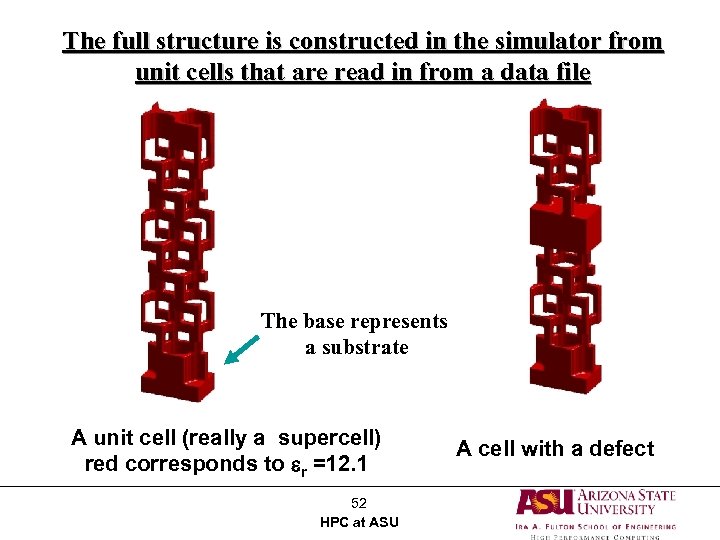
The full structure is constructed in the simulator from unit cells that are read in from a data file The base represents a substrate A unit cell (really a supercell) red corresponds to er =12. 1 52 HPC at ASU A cell with a defect
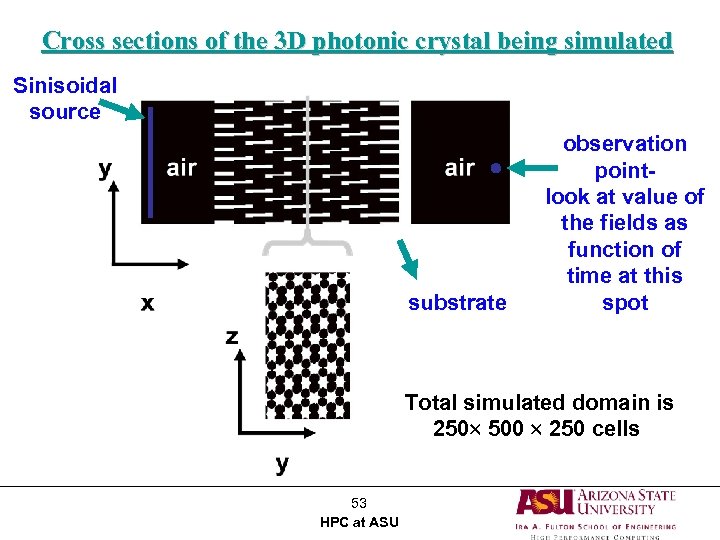
Cross sections of the 3 D photonic crystal being simulated Sinisoidal source substrate observation pointlook at value of the fields as function of time at this spot Total simulated domain is 250 500 250 cells 53 HPC at ASU
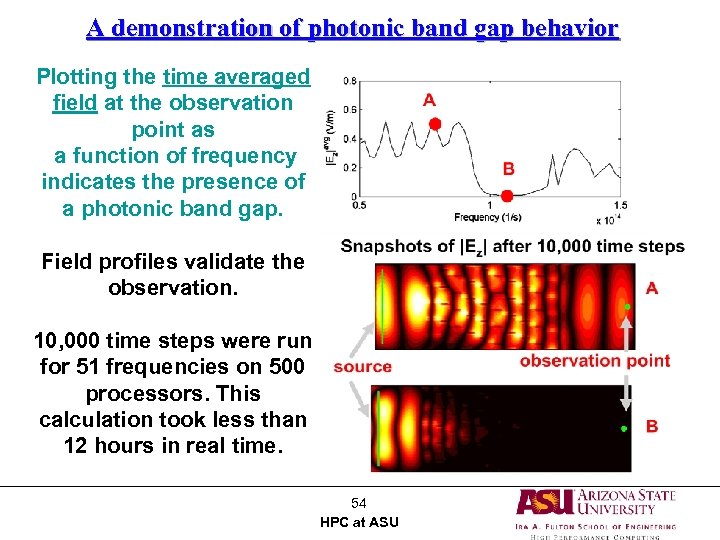
A demonstration of photonic band gap behavior Plotting the time averaged field at the observation point as a function of frequency indicates the presence of a photonic band gap. Field profiles validate the observation. 10, 000 time steps were run for 51 frequencies on 500 processors. This calculation took less than 12 hours in real time. 54 HPC at ASU
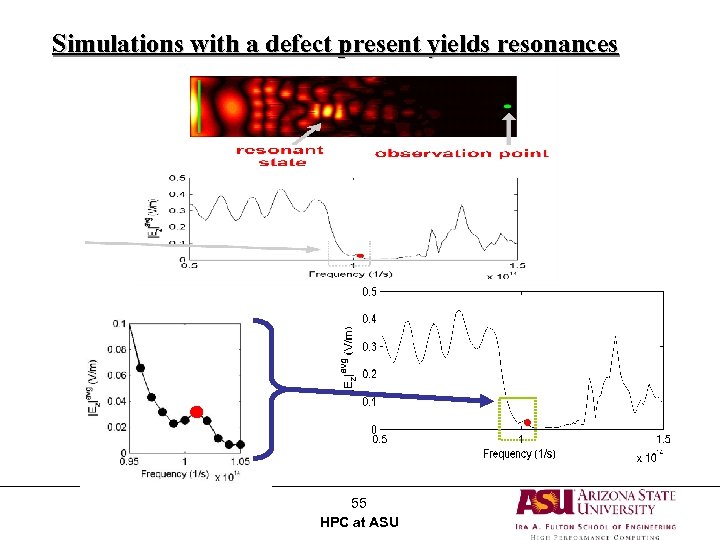
Simulations with a defect present yields resonances 55 HPC at ASU
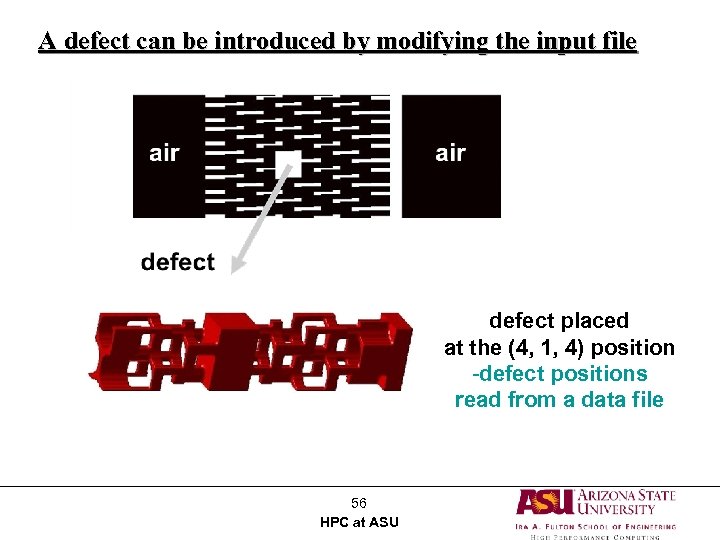
A defect can be introduced by modifying the input file defect placed at the (4, 1, 4) position -defect positions read from a data file 56 HPC at ASU
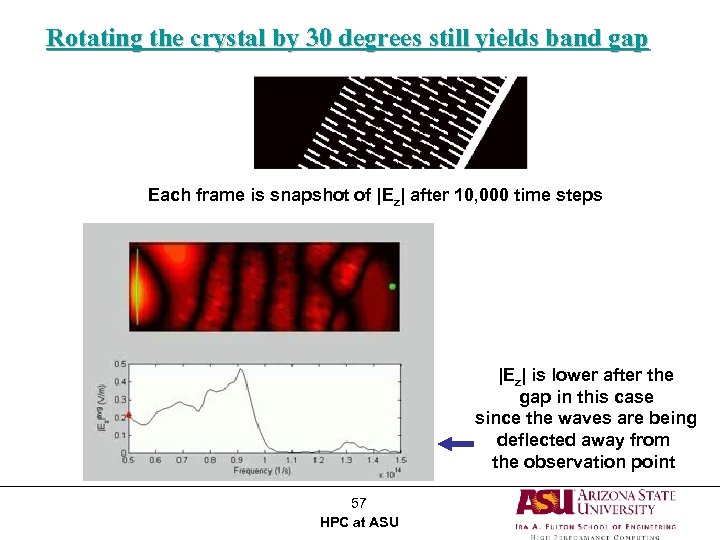
Rotating the crystal by 30 degrees still yields band gap Each frame is snapshot of |Ez| after 10, 000 time steps |Ez| is lower after the gap in this case since the waves are being deflected away from the observation point 57 HPC at ASU
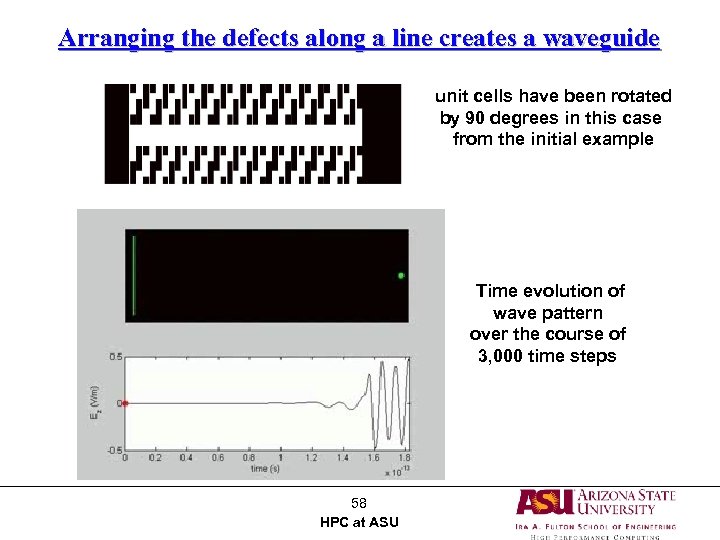
Arranging the defects along a line creates a waveguide unit cells have been rotated by 90 degrees in this case from the initial example Time evolution of wave pattern over the course of 3, 000 time steps 58 HPC at ASU
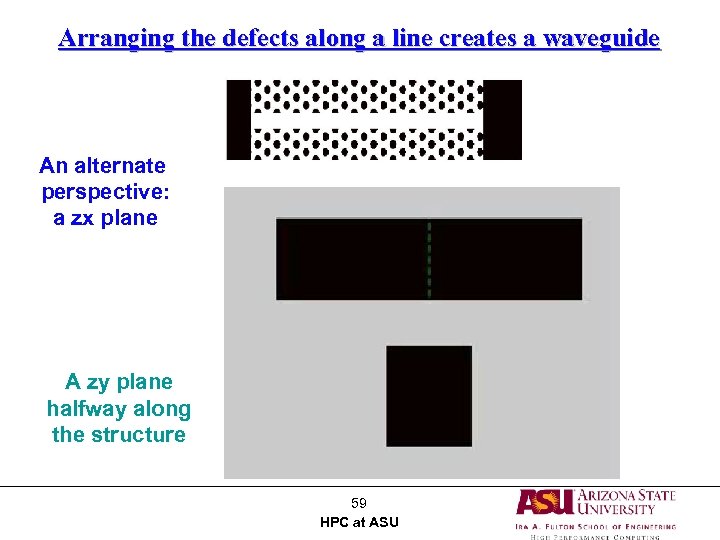
Arranging the defects along a line creates a waveguide An alternate perspective: a zx plane A zy plane halfway along the structure 59 HPC at ASU

An example of a larger scale simulation Cross section of a simulation done on a 1000 × 1000 domain (109 grid points) frequency set to be in the crystal’s band 60 HPC at ASU

Transport in Open Quantum Dot Systems Dr. Richard Akis Dept. of Electrical Engineering, Arizona State University Dr. Gil Speyer High Performance Computing Center, Arizona State University 61 HPC at ASU
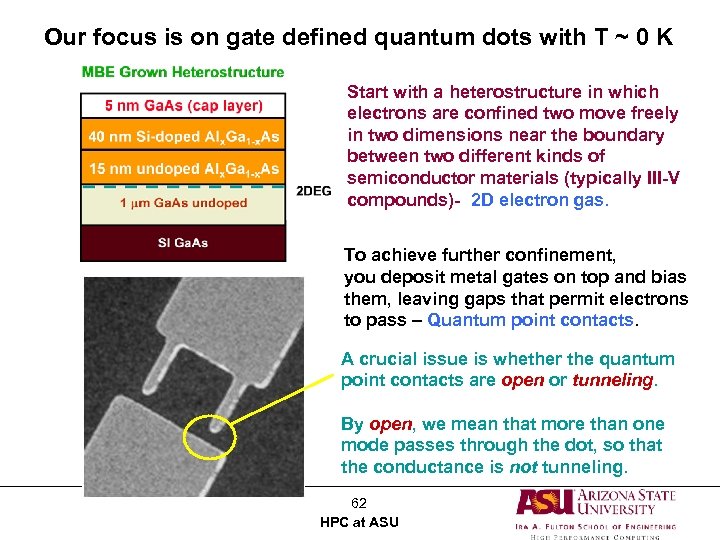
Our focus is on gate defined quantum dots with T ~ 0 K Start with a heterostructure in which electrons are confined two move freely in two dimensions near the boundary between two different kinds of semiconductor materials (typically III-V compounds)- 2 D electron gas. To achieve further confinement, you deposit metal gates on top and bias them, leaving gaps that permit electrons to pass – Quantum point contacts. A crucial issue is whether the quantum point contacts are open or tunneling. By open, we mean that more than one mode passes through the dot, so that the conductance is not tunneling. 62 HPC at ASU
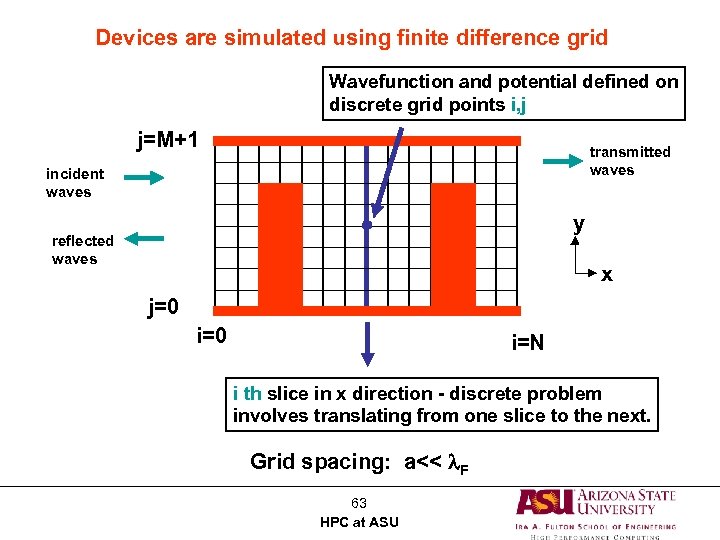
Devices are simulated using finite difference grid Wavefunction and potential defined on discrete grid points i, j j=M+1 transmitted waves incident waves y reflected waves x j=0 i=N i th slice in x direction - discrete problem involves translating from one slice to the next. Grid spacing: a<< l. F 63 HPC at ASU

Discrete Schrodinger Equation in 2 D Standard SE: i, j+1 Replace derivatives with finite differences: x=ai, y= aj a a i-1, j a i, j-1 SE on the finite difference lattice reads: (1 a) where is the “hopping” term 64 HPC at ASU i+1, j
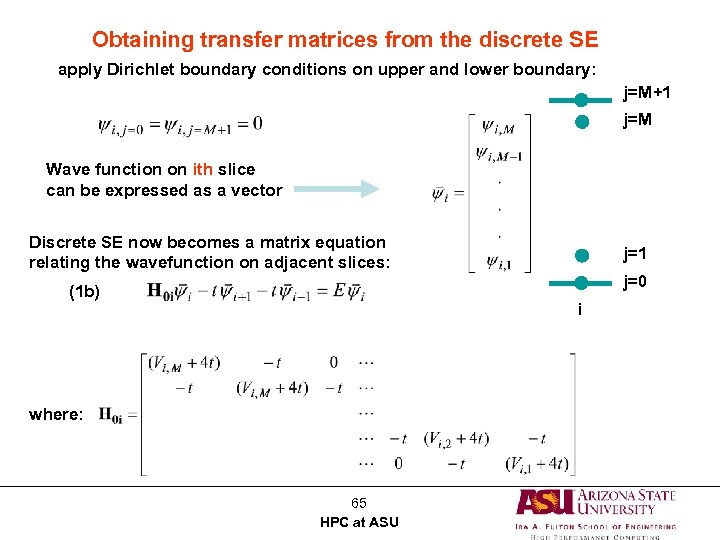
Obtaining transfer matrices from the discrete SE apply Dirichlet boundary conditions on upper and lower boundary: j=M+1 j=M Wave function on ith slice can be expressed as a vector Discrete SE now becomes a matrix equation relating the wavefunction on adjacent slices: (1 b) j=1 j=0 i where: 65 HPC at ASU

(1 b) can be rewritten as: Combining this with the trivial equation one obtains: (2) Is the transfer matrix relating adjacent slices where Modification for a perpendicular magnetic field (0, 0, B) : B enters into phase factors important quantity: flux per unit cell 66 HPC at ASU

yields the modes on the left side of the system Solving the eigenvalue problem: Mode eigenvectors have the generic form: redundant There will be M modes that propagates to the right (+) with eigenvalues: propagating evanescent There will be M modes that propagates to the left (+) with eigenvalues: propagating evanescent defining and Complete matrix of eigenvectors: 67 HPC at ASU
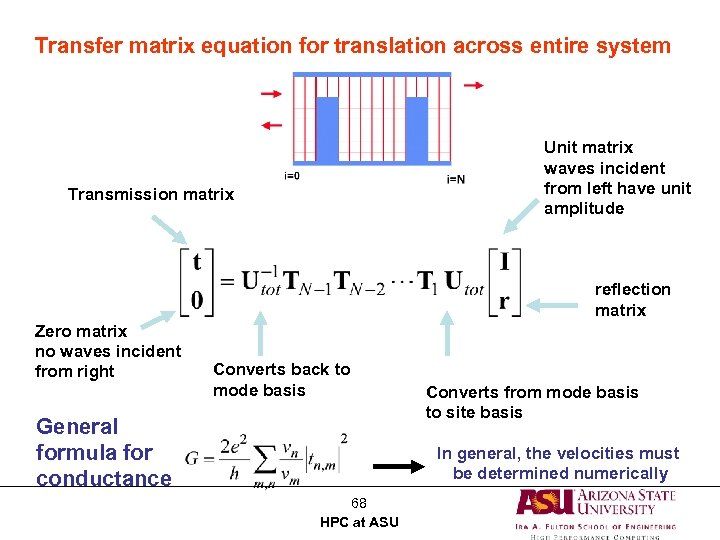
Transfer matrix equation for translation across entire system Unit matrix waves incident from left have unit amplitude Transmission matrix reflection matrix Zero matrix no waves incident from right Converts back to mode basis General formula for conductance Converts from mode basis to site basis In general, the velocities must be determined numerically 68 HPC at ASU
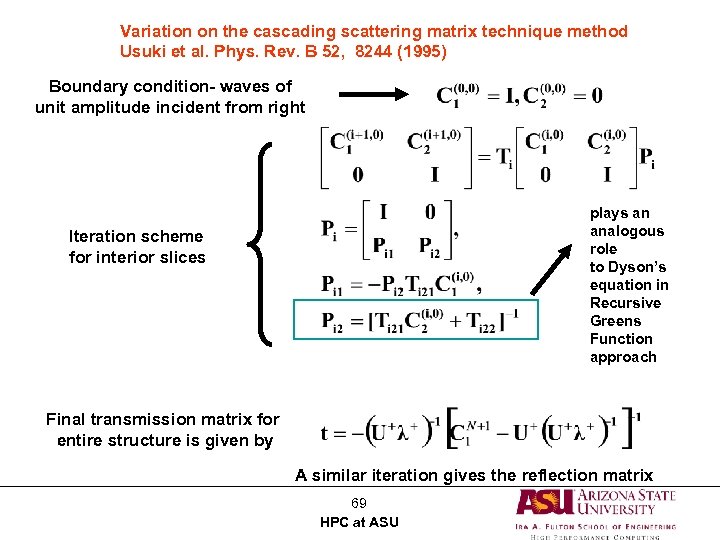
Variation on the cascading scattering matrix technique method Usuki et al. Phys. Rev. B 52, 8244 (1995) Boundary condition- waves of unit amplitude incident from right plays an analogous role to Dyson’s equation in Recursive Greens Function approach Iteration scheme for interior slices Final transmission matrix for entire structure is given by A similar iteration gives the reflection matrix 69 HPC at ASU

Comparing the spectrum with the magnetoconductance 15. 5 0 1 3 Spectra lines from closed dot spectrum are reflected in the conductance of the open dot, but a modified resonant structure occurs due to the nature of the coupling of the dot with the external environmentthe broadening is nonuniform 9 14. 0 15. 5 14. 0 -0. 25 B (T) 0. 25 -0. 25 B (T) 70 HPC at ASU 0. 25

As mentioned earlier, the states that survive the opening to the external environment to yield resonances in the conductance are referred to as pointer states. What is their nature? One important aspect to them is that they can be associated with classical periodic orbits- their wave functions tend to be “scarred”. 71 HPC at ASU
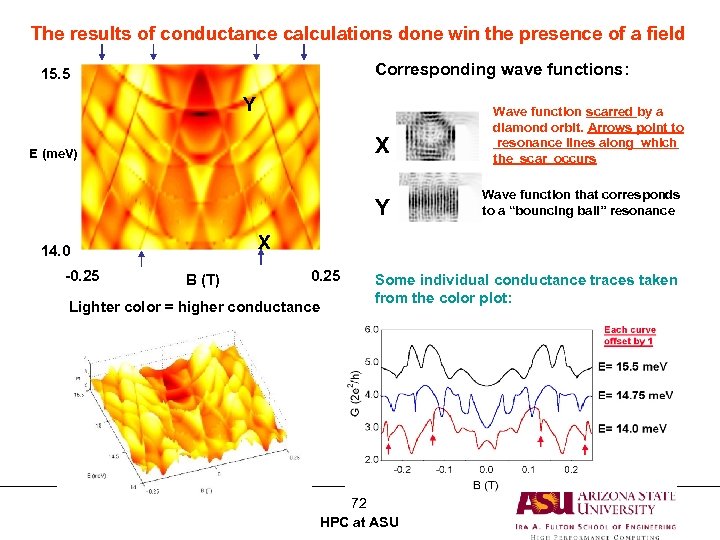
The results of conductance calculations done win the presence of a field Corresponding wave functions: 15. 5 Y X E (me. V) Y Wave function that corresponds to a “bouncing ball” resonance X 14. 0 -0. 25 Wave function scarred by a diamond orbit. Arrows point to resonance lines along which the scar occurs B (T) 0. 25 Lighter color = higher conductance Some individual conductance traces taken from the color plot: 72 HPC at ASU
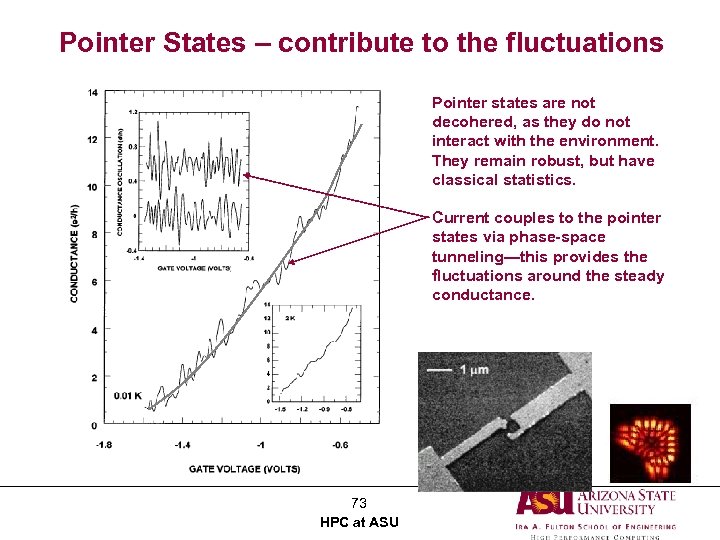
Pointer States – contribute to the fluctuations Pointer states are not decohered, as they do not interact with the environment. They remain robust, but have classical statistics. Current couples to the pointer states via phase-space tunneling—this provides the fluctuations around the steady conductance. 73 HPC at ASU
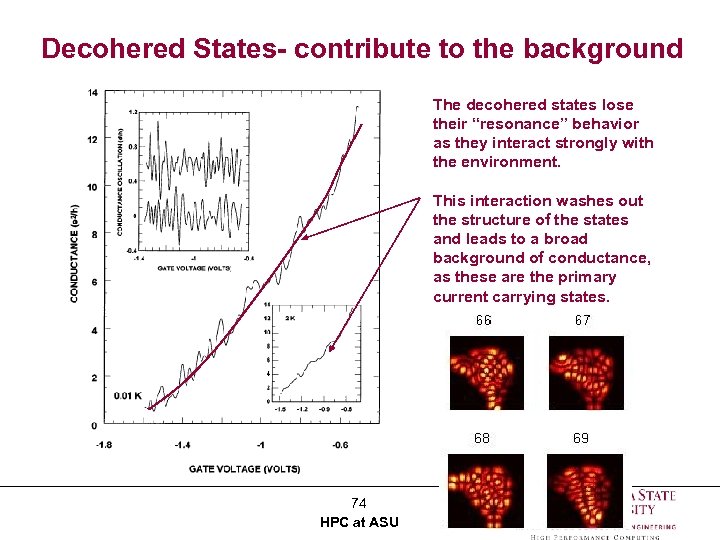
Decohered States- contribute to the background The decohered states lose their “resonance” behavior as they interact strongly with the environment. This interaction washes out the structure of the states and leads to a broad background of conductance, as these are the primary current carrying states. 74 HPC at ASU
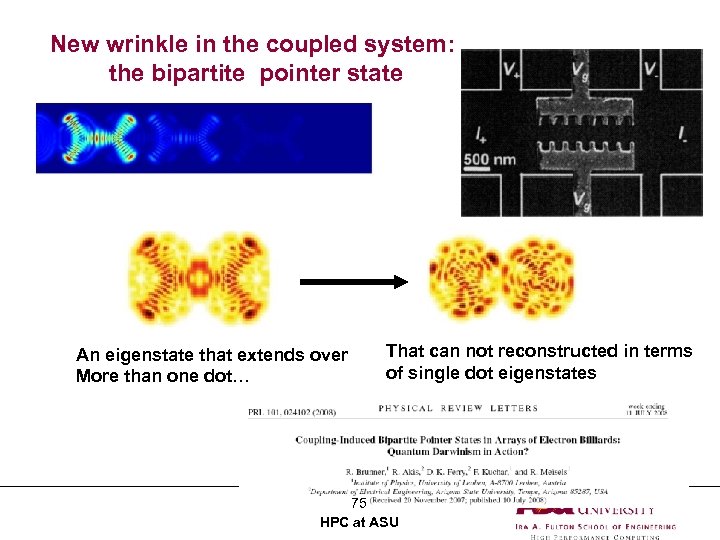
New wrinkle in the coupled system: the bipartite pointer state An eigenstate that extends over More than one dot… That can not reconstructed in terms of single dot eigenstates 75 HPC at ASU

Why Parallelize this code? • Cascaded scattering matrix code should exhibit scalable parallelism – can solve larger problems w/more procs • Number of points in slice, n, limited by eigensolver • Matrix routines are fairly straightforward and have implementations in Sca. LAPACK library • With distributed memory, large number of n. Xn arrays can be kept to a reasonable size 76 HPC at ASU
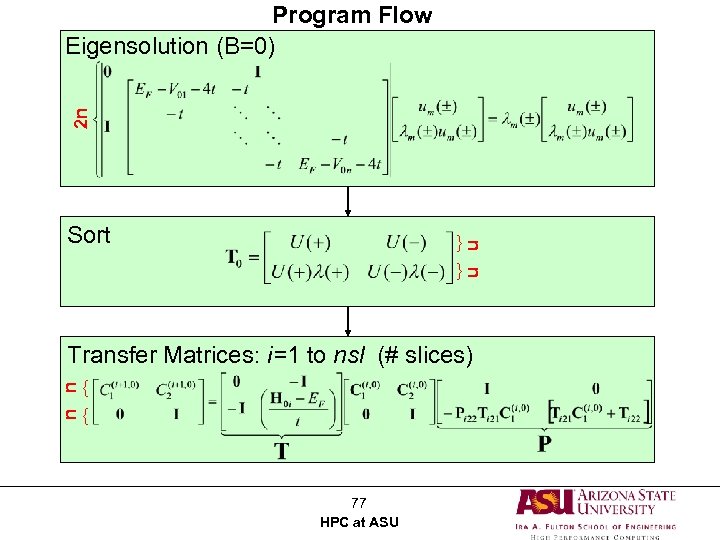
2 n Program Flow Eigensolution (B=0) n n Sort { { n n Transfer Matrices: i=1 to nsl (# slices) { { 77 HPC at ASU
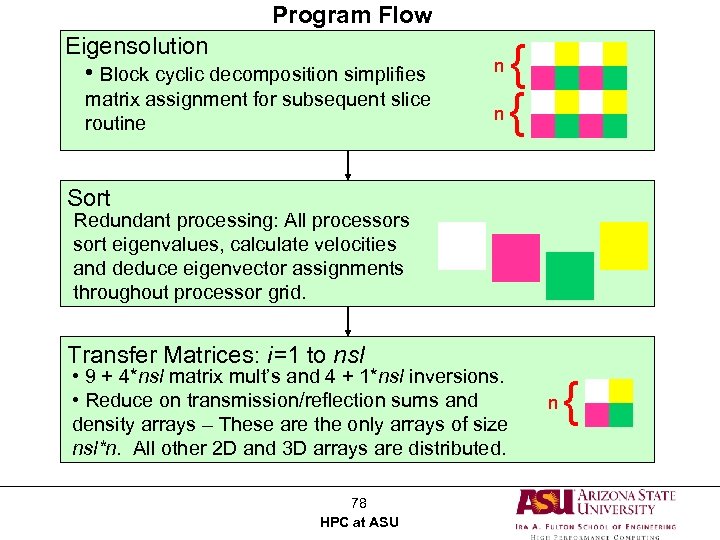
Program Flow Eigensolution • Block cyclic decomposition simplifies n matrix assignment for subsequent slice routine n { { Sort Redundant processing: All processors sort eigenvalues, calculate velocities and deduce eigenvector assignments throughout processor grid. Transfer Matrices: i=1 to nsl • 9 + 4*nsl matrix mult’s and 4 + 1*nsl inversions. • Reduce on transmission/reflection sums and density arrays – These are the only arrays of size nsl*n. All other 2 D and 3 D arrays are distributed. 78 HPC at ASU n {
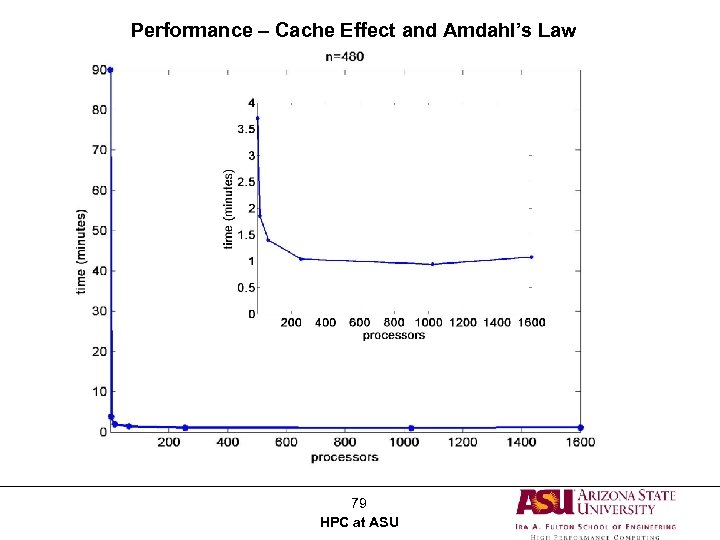
Performance – Cache Effect and Amdahl’s Law 79 HPC at ASU
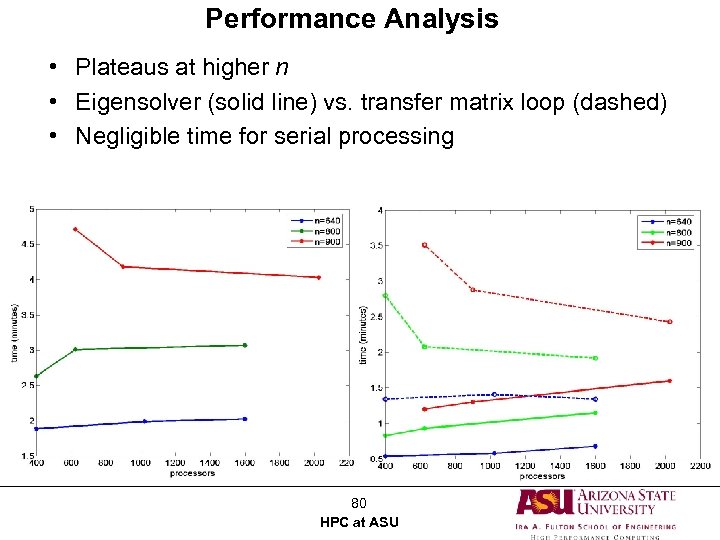
Performance Analysis • Plateaus at higher n • Eigensolver (solid line) vs. transfer matrix loop (dashed) • Negligible time for serial processing 80 HPC at ASU
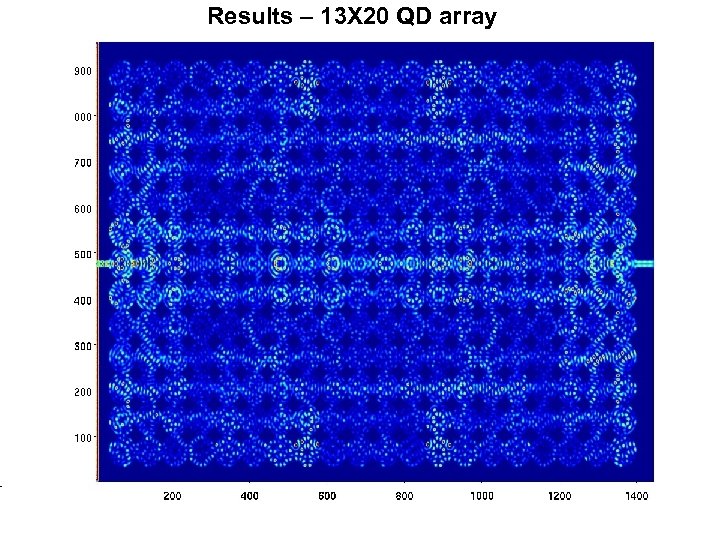
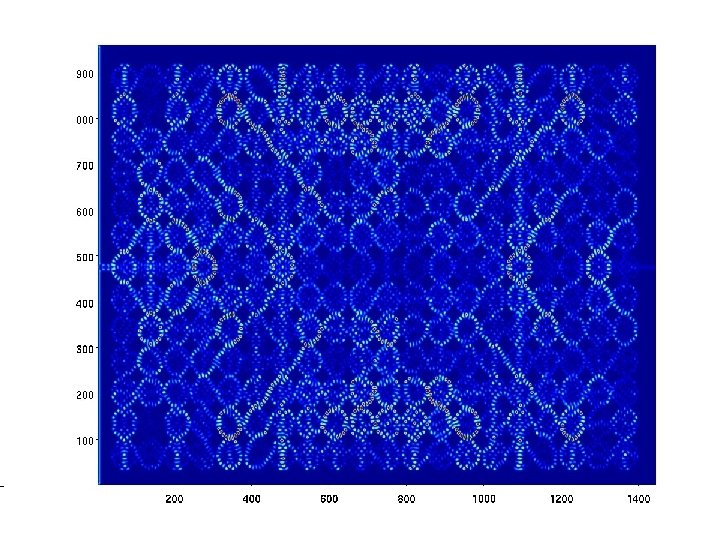
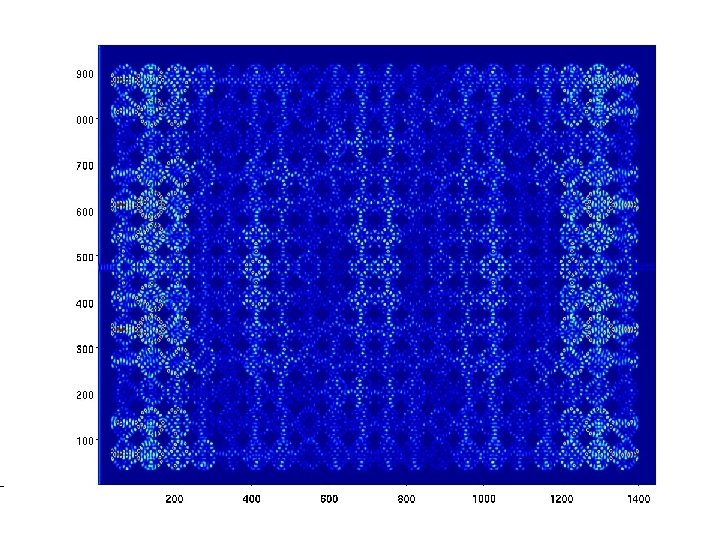
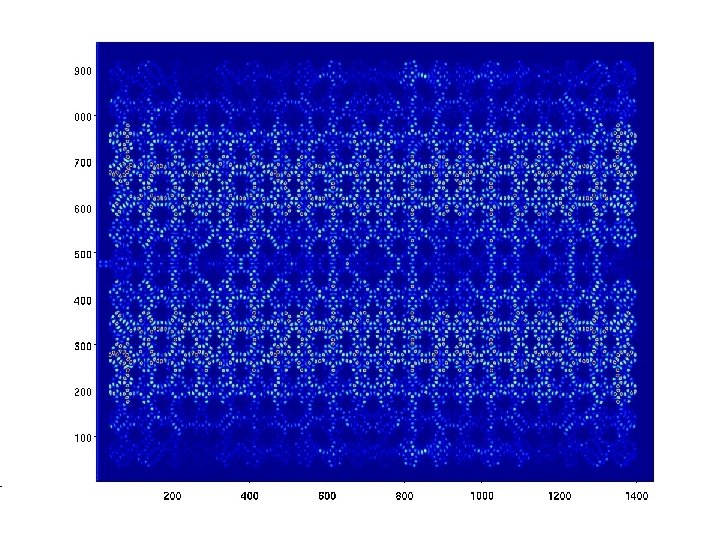
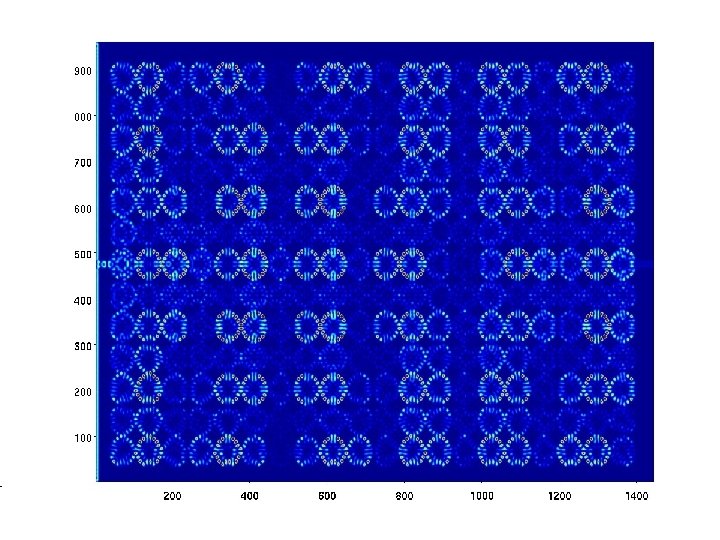
Results – 13 X 20 QD array HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
HPC at ASU
c4bfd11966494f30a404910cf29b178b.ppt