Затухающие колебания Затухающие электромагнитные колебания
Дифференциальное уравнение затухающих колебаний в колебательном контуре Когда конденсатор заряжен, напряжение на нем можно выразить, используя закон Ома: где ε - ЭДС самоиндукции, возникающая в катушке, i - сила тока, R сопротивление катушки. Если R не мало и им нельзя пренебречь, то
Дифференциальное уравнение затухающих колебаний в колебательном контуре Напряжение на конденсаторе Знак «-» означает, что протекание тока в цепи связано с убыванием заряда конденсатора (по цепи проходит тот заряд, который ушел с обкладок конденсатора)
Уравнение затухающих электромагнитных колебаний Дифференциальное уравнение можно переписать в виде Или где Полученное уравнение аналогично уравнению затухающих механических колебаний. Его решение аналогично решению уравнения для механических колебаний.
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. (1) В уравнение (1) подставим функцию ристическое уравнение: и получим характе- - характеристическое уравнение.
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. Корни этого характеристического уравнения: Как известно, общим решением дифференциального уравнения второго порядка с постоянными коэффициентами является функция: Подкоренные выражения в формулах, определяющих корни характеристического уравнения, в зависимости от значений параметров и могут быть как положительными, так и отрицательными. Это приводит к тому, что существует два класса решений.
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. 1. Если 0, то подкоренное выражение будет отрицательным, а корни характеристического уравнения – комплексными. Обозначим тогда Решение уравнения в этом случае будет иметь вид: Или в действительной форме: Здесь A и 0 – произвольные постоянные имеющие смысл амплитуды и начальной фазы колебаний,
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. 2. Если > 0, то подкоренные выражения в формулах, определяющих корни характеристического уравнения будут положительными, а корни характеристического уравнения 1 и 2 – действительными.
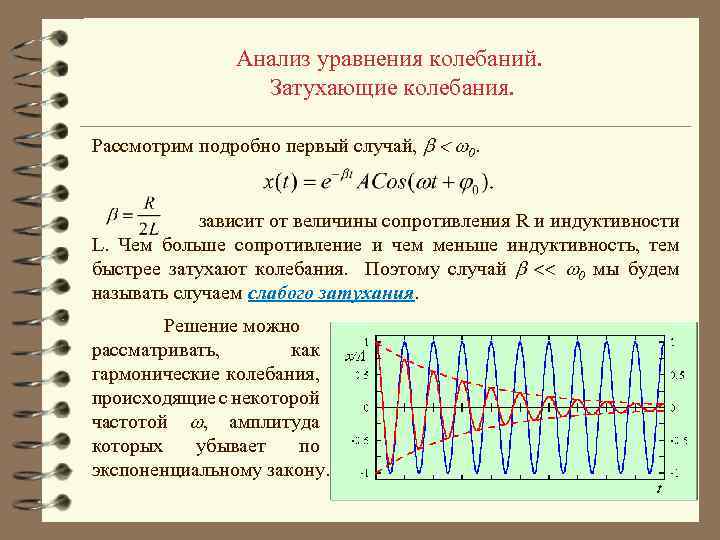
Анализ уравнения колебаний. Затухающие колебания. Рассмотрим подробно первый случай, 0. зависит от величины сопротивления R и индуктивности L. Чем больше сопротивление и чем меньше индуктивность, тем быстрее затухают колебания. Поэтому случай 0 мы будем называть случаем слабого затухания. Решение можно рассматривать, как гармонические колебания, происходящие с некоторой частотой , амплитуда которых убывает по экспоненциальному закону.
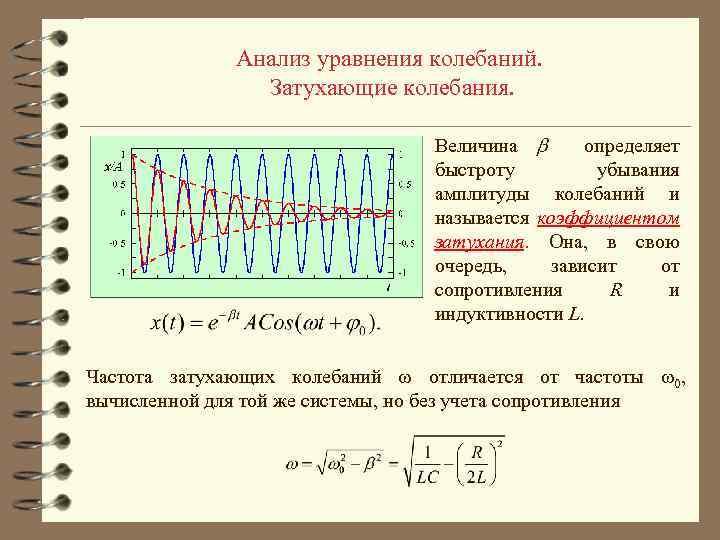
Анализ уравнения колебаний. Затухающие колебания. Величина определяет быстроту убывания амплитуды колебаний и называется коэффициентом затухания. Она, в свою очередь, зависит от сопротивления R и индуктивности L. Частота затухающих колебаний отличается от частоты 0, вычисленной для той же системы, но без учета сопротивления
Анализ уравнения колебаний. Затухающие колебания. Период затухающих колебаний: Для случая слабого затухания, когда 0, различие частот и периодов несущественно и часто при решении практических задач в случае слабого затухания период и частоту колебаний определяют по формулам для свободных (незатухающих) колебаний.
Анализ решения уравнения колебаний. Апериодический процесс. Как мы видим, условием возникновения апериодического процесса является > 0, то есть Это возможно, если сопротивление Если же в системе возникнут затухающие колебания.
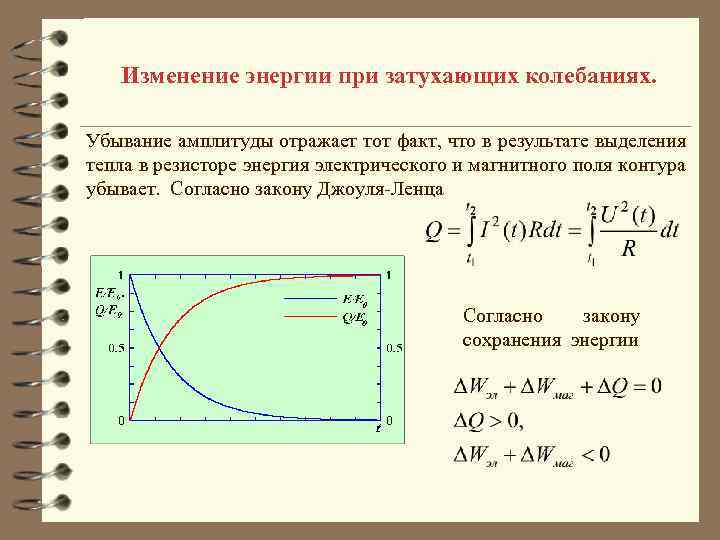
Изменение энергии при затухающих колебаниях. Убывание амплитуды отражает тот факт, что в результате выделения тепла в резисторе энергия электрического и магнитного поля контура убывает. Согласно закону Джоуля-Ленца Согласно закону сохранения энергии
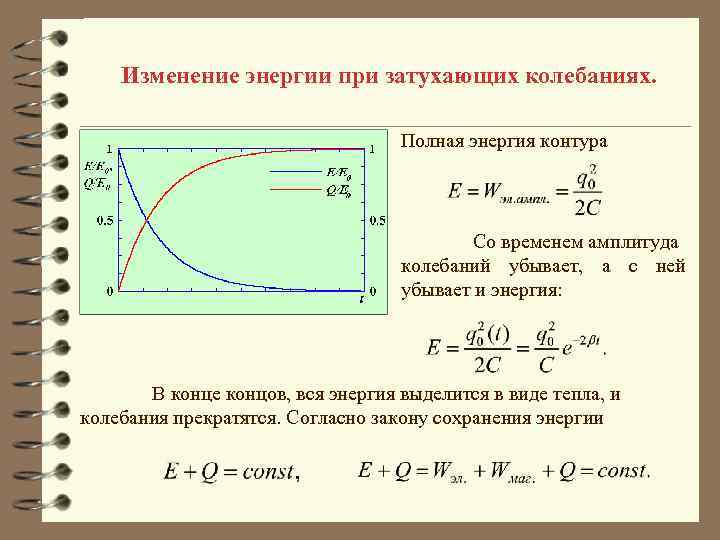
Изменение энергии при затухающих колебаниях. Полная энергия контура Со временем амплитуда колебаний убывает, а с ней убывает и энергия: В конце концов, вся энергия выделится в виде тепла, и колебания прекратятся. Согласно закону сохранения энергии
Величины, характеризующие процесс затухания колебаний. Параметры затухания Коэффициент затухания для электромагнитных Декремент и логарифмический декремент затухания: Время релаксации Добротность колебаний.
Скачать презентацию Затухающие колебания Затухающие электромагнитные колебания Дифференциальное уравнение
Лекция 30. Затухающие колебания часть 2.pptx