Скачать презентацию Защита информации Тема 8 Системы электронной подписи 12
08 Системы электронной подписи.pptx
- Количество слайдов: 30
Защита информации Тема 8. Системы электронной подписи 12. 02. 2018 ИГЭУ. Кафедра ПОКС
Системы электронной подписи (ЭЦП) В кон це ись ма ли до ку мен та п и обыч но та вится од пись, то с п ч пре сле ду ет две це ли : 1) по лу ча тель име ет воз мож ность убе дить ся ис тин но сти в пись ма, сли чив под пись с имею щим ся у не го об раз цом; 2) лич ная под пись яв ля ет ся юри ди че ским га ран том ав тор ст ва до ку мен та. В со вре мен ном и ре элек трон ных форм до ку мен тов м ак ту аль ной ста ла про бле ма уста нов ле ния под лин но сти и ав тор ст ва без бу маж ной до ку мен та ции. Это позволяет делать электронно цифровая подпись. Защита информации. 08 Системы электронной подписи 2
От ка ких на ру ше ний за щи щает ЭЦП? Пусть Александр (А) послал письмо Борису (Б): А Б. 1. От каз (ре не гат ст во). Александр за яв ля ет, он не по сы лал что со об ще ние Борису, хо тя на са мом де ле он все та ки по сы лал. 2. Мо ди фи ка ция (пе ре дел ка). Борис из ме ня ет со об ще ние и ут вер жда ет, что дан ное (из ме нен ное) со об ще ние по слал му Александр; или Владимир е пе ре хва ты ва ет со об ще ние ме ж ду Александром и Борисом с це лью его скры той мо ди фи ка ции. 3. Под дел ка. Борис фор ми ру ет . со об ще ние ут вер жда ет, дан ное и что (из ме нен ное) со об ще ние по слал ему Александр. 4. Мас ки ров ка (ими та ция)Владимир по сы ла ет . Борису со об ще ние от име ни Александра. 5. По втор Владимир по вто ря ет . ра нее е ре дан ное п со об ще ние, ко то рое Александр по сы лал а нее Борису. Не смот ря на то, что при ни ма ют ся р все воз мож ные е ры за щи ты от по вто ров, имен но на этот ме тод м при хо дит ся боль шин ст во слу ча ев е за кон но го н сня тия и тра ты де нег в сис те мах элек трон ных пла те жей. Защита информации. 08 Системы электронной подписи 3
ЭЦП на основе симметричного шифрования Данная схема предусматривает наличие третьей стороны (арбитра), пользующегося доверием участников обмена подписанными электронными документами (ЭД). 1. Участник A зашифровывает сообщение на своем секретном ключе KA, значение которого разделено с арбитром. Вместе с сообщением шифруется и информация об адресате (Б). Сообщение передается арбитру. 2. Арбитр расшифровывает полученное сообщение на ключе KA. К сообщению добавляется информация о том, что оно пришло от участника A. Затем сообщение зашифровывается на ключе участника Б (KБ) и посылается ему. 3. Участник Б расшифровывает данное сообщение и убеждается в том, что отправителем является участник A. Авторизацией документа в данной схеме будет считаться сам факт зашифрования ЭД секретным ключом и передача его арбитру. Защита информации. 08 Системы электронной подписи 4
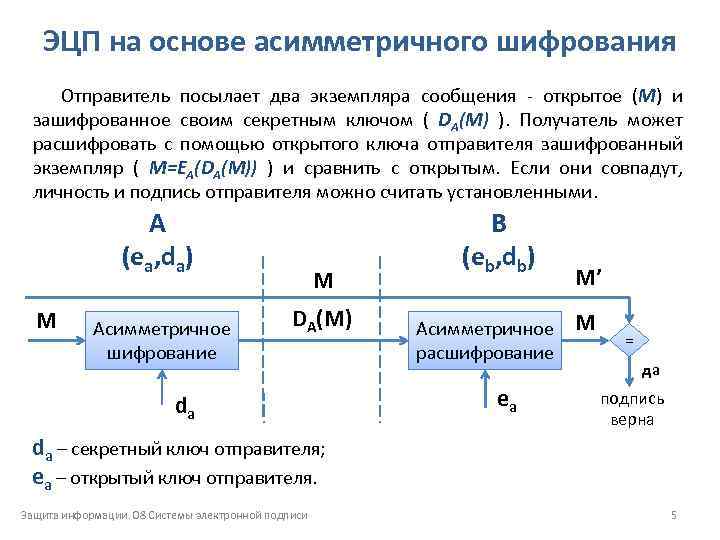ЭЦП на основе асимметричного шифрования Отправитель посылает два экземпляра сообщения открытое (M) и зашифрованное своим секретным ключом ( DA(M) ). Получатель может расшифровать с помощью открытого ключа отправителя зашифрованный экземпляр ( M=EA(DA(M)) ) и сравнить с открытым. Если они совпадут, личность и подпись отправителя можно считать установленными. А (ea, da) M Асимметричное шифрование M DA(M) da B (eb, db) Асимметричное расшифрование ea M’ M = да подпись верна da – секретный ключ отправителя; ea – открытый ключ отправителя. Защита информации. 08 Системы электронной подписи 5
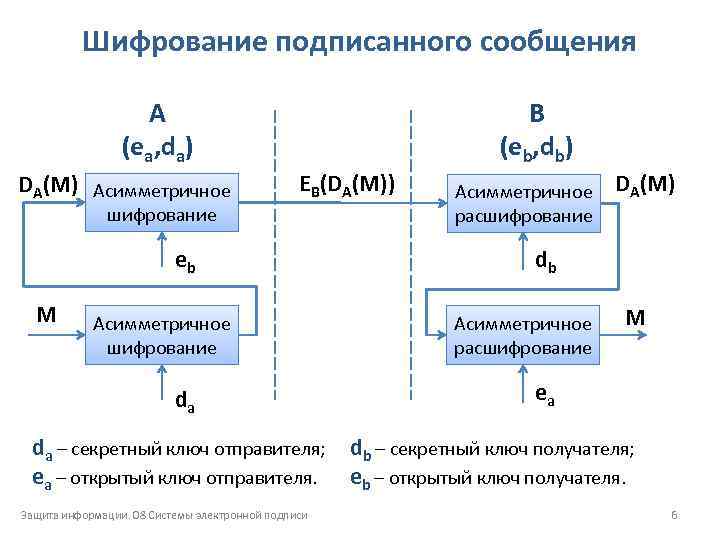Шифрование подписанного сообщения А (ea, da) DA(M) Асимметричное B (eb, db) EB(DA(M)) шифрование eb M Асимметричное шифрование da da – секретный ключ отправителя; ea – открытый ключ отправителя. Защита информации. 08 Системы электронной подписи Асимметричное расшифрование DA(M) db Асимметричное расшифрование M ea db – секретный ключ получателя; eb – открытый ключ получателя. 6
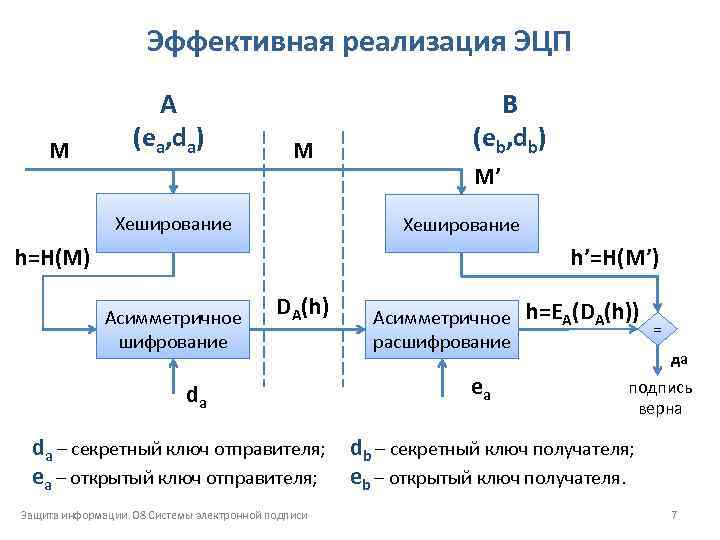Эффективная реализация ЭЦП M А (ea, da) M Хеширование B (eb, db) M’ Хеширование h=H(M) h’=H(M’) Асимметричное шифрование DA(h) da da – секретный ключ отправителя; ea – открытый ключ отправителя; Защита информации. 08 Системы электронной подписи Асимметричное расшифрование ea h=EA(DA(h)) = да подпись верна db – секретный ключ получателя; eb – открытый ключ получателя. 7
Cертификационные центры При использовании асимметричных методов необходимо иметь гарантию подлинности пары (имя, открытый ключ) адресата. Для решения этой задачи вводится понятие сертификационного центра, который заверяет справочник имен/ключей своей подписью. Защита информации. 08 Системы электронной подписи 8
Криптографические методы позволяют надежно контролировать целостность информации. В отличие от традиционных методов контрольного суммирования, способных противостоять только случайным ошибкам, криптографическая контрольная сумма (имитовставка), вычисленная с применением секретного ключа, практически исключает все возможности незаметного изменения данных. Цифровая сигнатура это строка символов, зависящая как от идентификатора отправителя, так и содержания сообщения. Ни кто, да же сам поль зо ва тель не мо жет из ме нить по слан но го со об ще ния так, ч сиг на ту ра ос та лась не из мен ной. Защита информации. 08 Системы электронной подписи 9
Расширенный алгоритм Евклида Пусть a и b – два целых положительных числа. Тогда существуют целые (не обязательно положительные) числа x и y, такие, что ax + by = НОД(a, b). (1) Расширенный алгоритм Евклида служит для отыскания НОД(a, b), x и y, удовлетворяющих данному равенству. Введем три вектора U = (u 1, u 2, u 3), V = (v 1, v 2, v 3), T = (t 1, t 2, t 3). ВХОД: Положительные целые числа a, b, a >= b. ВЫХОД: НОД(a, b), x, y, ax + by = НОД (a, b). U (a, 1, 0), V (b, 0, 1). WHILE v 1 <> 0 DO q u 1 div v 1; T (u 1 mod v 1, u 2 qv 2, u 3 – qv 3); U V, V T. RETURN U=( НОД(a, b), x, y). Защита информации. 08 Системы электронной подписи 10
Расширенный алгоритм Евклида Во многих задачах криптографии для заданных чисел c, m требуется найти такое число d < m, что cd mod m = 1. (2) Такое d существует тогда и только тогда, когда c и m взаимно простые числа. Число d называется инверсией c по модулю m и часто обозначается c 1 mod m. Естественно будет выглядеть запись cс 1 mod m = 1. Умножение на c 1 соответствует делению на с при вычислениях по модулю m. Покажем, как можно вычислить инверсию с помощью расширенного алгоритма Евклида. Равенство (2) означает, что для некоторого целого k cd km = 1. (3) Учитывая, что c и m взаимно просты, перепишем (3) в виде m( k) + cd = НОД(m, c). (4) Если число d получится отрицательным, то к нему надо прибавить m. Защита информации. 08 Системы электронной подписи 11
Расширенный алгоритм Евклида. Пример Найдем 3 1 mod 11. a = 11, b = 3, U 11 1 0 V U 3 0 1 T V U 2 1 T V U 1 1 4 T V 0 3 11 Получается: 3 1 mod 11 = 4 Защита информации. 08 Системы электронной подписи 3 q = 1 q = 2 12
Стандарты на ЭЦП ГОСТ 34. 10 94 "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма" и ГОСТ 34. 11 94 "Функция хеширования", объединенные общим заголовком "Информационная технология. Криптографическая защита информации", регламентируют вычисление дайджеста и реализацию электронной подписи. Защита информации. 08 Системы электронной подписи 13
ГОСТ Р 34. 10 94 Необходимо найти два простых числа, q длиной 256 бит и р длиной 1024 бита, между которыми выполняется соотношение p = bq + 1 (1) для некоторого целого b. Старшие биты в р и q должны быть равны единице. Затем выбирается число а > 1, такое, что aq mod р = 1. (2) В результате получаем три общих параметра — р , q и a. Замечание 1. Равенство (2) означает, что при возведении а в степени по модулю р показатели приводятся по модулю q , и такое приведение будет постоянно выполняться при генерации и проверке подписи. В результате длина показателей степени в рамках рассматриваемого алгоритма никогда не будет превышать 256 бит, что упрощает вычисления. Далее каждый пользователь выбирает случайно число х , 0 < х < q , и вычисляет y = ax mod p. (3) Число х будет секретным ключом пользователя, а число у — открытым ключом. Защита информации. 08 Системы электронной подписи 14
ГОСТ Р 34. 10 94 Пусть имеется сообщение m, которое необходимо подписать. Генерация подписи выполняется следующим образом: 1. Вычисляем значение хеш функции h = h(m) для сообщения m (в российском варианте хеш функция определяется ГОСТом P 34. 11 94). 2. Формируем случайное число k , 0 < k < q. 3. Вычисляем r = (ak mod p) mod q. Если оказывается, что r = 0 , то возвращаемся к шагу 2. 4. Вычисляем s = (kh + xr) mod q. Если s = 0 , то возвращаемся к шагу 2. 5. Получаем подписанное сообщение
ГОСТ Р 34. 10 94 Замечание 2. Чтобы найти параметр а, удовлетворяющий (2), рекомендуется использовать следующий метод. Берем случайное число g > 1 и вычисляем а = g(р 1)/q mod р. (4) Если а > 1, то это то, что нам нужно. Действительно, на основании (4) и теоремы Ферма имеем aq mod р = g((p 1)/q) q mod p = gp l mod p = 1, т. е. выполняется равенство (2). Если при вычислении по (4) мы получаем а = 1 (крайне маловероятный случай), то нужно просто взять другое число g. Защита информации. 08 Системы электронной подписи 16
ГОСТ Р 34. 10 94. Пример Выберем общие несекретные параметры: q = 11, р = 6 q + 1 = 67, возьмем g = 10 и вычислим а = 106 mod 67 = 25. Выберем секретный ключ х = 6 и вычислим открытый ключ: у = 256 mod 67 = 62. Сформируем подпись для сообщения m. Пусть для хеш функции этого сообщения h(m) = 3. Возьмем случайно число k = 8. Вычислим: r = (258 mod 67) mod 11 = 24 mod 11 = 2, s = (8 • 3 + 6 • 2) mod 11 = 36 mod 11 = 3. Получаем подписанное сообщение
Отличия FIPS 186 от ГОСТ Р 34. 10 94 Стандарт США FIPS 186 был принят в 1991 году. В основе обоих стандартов лежит по сути один и тот же алгоритм, называемый DSA (Digital Signature Algorithm) и являющийся вариацией подписи Эль Гамаля. Отличиях американского стандарта от российского. Они сводятся к следующему. 1. Длина числа q берется равной 160 бит. 2. В качестве хеш функции используется алгоритм SHA 1. 3. При генерации подписи на шаге 4 параметр s вычисляется по формуле s = k 1(h + xr) mod q. 4. При проверке подписи на шаге 3 u 1 и u 2 вычисляются по формулам u 1 = h • s 1 mod q , u 2 = r • s 1 mod q. Защита информации. 08 Системы электронной подписи 18
Криптосистемы на эллиптических кривых Исполь зование эллиптических кривых в криптографических целях было впервые предложено Коблицом и Миллером в 1985 году. В 1998 году были приняты стандарты США ANSI X 9. 62 и FIPS 186 2, а в 2001 году аналогичный российский стандарт ГОСТ Р 34. 10 2001. Нил Коблиц Neal Koblitz Виктор Миллер Victor Miller Криптографические алгоритмы, основанные на эллиптических кривых имеют более высокую стойкость (по отношению к другим асимметричным алгоритмам) при равной трудоемкости. Это объяс няется тем, что для вычисления обратных функций на эллиптических кривых известны только алгоритмы с экспоненциальным ростом трудо емкости, тогда как для обычных систем предложены субэкспоненциаль ные етоды. В результате м тот уровень стойкости, который достигается, скажем, в RSA при использовании 1024 битовых модулей, в системах на эллиптических кривых реализуется при размере модуля 160 бит. Защита информации. 08 Системы электронной подписи 19
Математические основы Кривая третьего порядка Е , задаваемая уравнением вида Е: Y 2 = X 3 + а. Х + b, (1) называется эллиптической кривой. Поскольку Y = ± Х 3 + а. Х + b , график кривой симметричен от носительно оси абсцисс. Чтобы найти точки его пересечения с осью абсцисс, необходимо решить кубическое уравнение X 3 + а. Х + b = 0, (2) используя известные формулы Кардано. Дискриминант этого уравне ния a) D < 0; б) D = 0; в) D > 0. 20
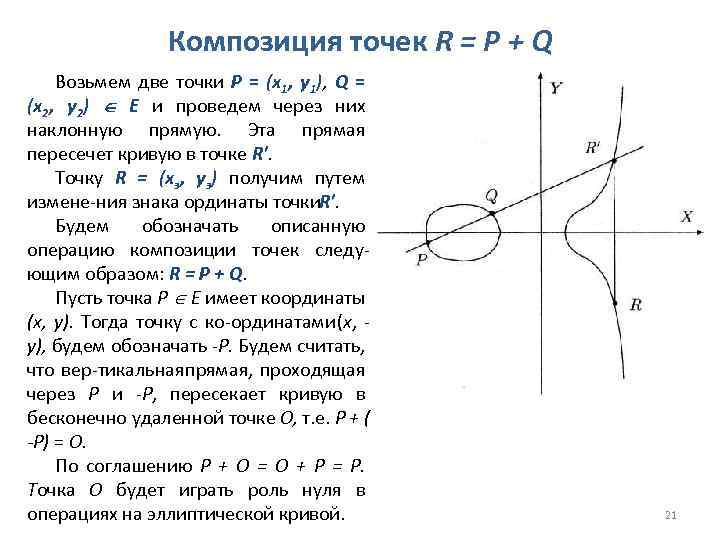Композиция точек R = Р + Q Возьмем две точки Р = (x 1, y 1), Q = (x 2, y 2) Е и проведем через них наклонную прямую. Эта прямая пересечет кривую в точке R'. Точку R = (хз, уз) получим путем измене ния знака ординаты точки '. R Будем обозначать описанную операцию композиции точек следу ющим образом: R = Р + Q. Пусть точка Р Е имеет координаты (х, у). Тогда точку с ко ординатами (х, у), будем обозначать Р. Будем считать, что вер тикальная прямая, проходящая через Р и Р, пересекает кривую в бесконечно удаленной точке О, т. е. Р + ( -Р) = O. По соглашению Р + О = О + Р = Р. Точка О будет играть роль нуля в Защита информации. 08 Системы электронной подписи операциях на эллиптической кривой. 21
![Удвоение точки R = Р + Р = [2]Р Теперь представим, что точки Р](https://present5.com/presentation/147431647_387075038/image-22.jpg "Удвоение точки R = Р + Р = [2]Р Теперь представим, что точки Р")
Удвоение точки R = Р + Р = [2]Р Теперь представим, что точки Р и Q сближаются друг с другом и, наконец, сливаются в одну точку Р = Q = (x 1, y 1). Тогда композиция R = (хз, yз) = Р+Q = Р+Р будет получена путем проведения касательной в точке Р и отражения ее второго пересечения с кривой R' относительно оси абсцисс. Используем следующее обозначение: R = Р + Р = [2]Р. Композицию точек часто называют сложением точек. Удобно ввести следующие обозначения: [m]P = Р + Р+…+ Р (m слагаемых), [0]Р = О, [ т]Р = ( Р + Р+…+ Р) (m слагаемых). Защита информации. 08 Системы электронной подписи 22
Обозначим через k угловой коэффициент прямой. . Тогда формулы для вычисления координат точки R: x 3 = k 2 – x 1 – x 2, y 3 = k ( x 1 – x 3 ) – y 1, (5) (6) (7) (8) В криптографии используется кривая Ер(a, b): Y 2 = X 3 + а. Х + b (mod p). (9) В уравнении (9) переменные X, Y и коэффициенты a, b, где a, b < р , принимают целочисленные значения, а все вычисления выполняются по модулю р. В соответствии с (4) на a, b накладывается ограничение (4 а 3 + 27 b 2) mod р ≠ 0. (10) Количе ство точек в будем обозначать Ер(а, b). # Защита информации. 08 Системы электронной подписи 23
Элиптические кривые. Пример Рассмотрим кривую E 7(2, 6): Y 2 = Х 3 + 2 Х + 6 (mod 7). (11) Проверим условие (10): 4 • 23 + 27 • 62 = 4 • 1 + 6 • 1 = 3 ≠ 0 (mod 7). Данная кривая несингулярна. Найдем какую нибудь (случайную) точку. Пусть x = 5. Тогда Y 2 = 5 3 + 2 • 5 + 6 = 6 + 3 + 6 = 1 (mod 7) и у = 1 (mod 7) или у = 1 = 6 (mod 7). Мы нашли сразу две точки: (5, 1) и (5, 6). Найдем еще пару точек путем вычисления композиции. Вначале найдем [2](5, 1). Используя (8), (6) и (7), вычисляем Мы получили [2](5, 1) = (4, 6) (можно убедиться, что полученная точка лежит на кривой, подставив ее координаты в уравнение (10) ). Найдем еще одну точку [3](5, 1) = (5, 1) + (4, 6). Используя (5), (6) и (7), вычисляем х3 = 22 – 5 – 4 = 2 (mod 7), у3 = 2 · (5 – 2) – 1 = 2 · 3 – 1 = 5 (mod 7). Мы получили [3](5, 1) = (2, 5). Итак, мы нашли четыре точки. Защита информации. 08 Системы электронной подписи 24
ЭЦП на эллиптической кривой (ГОСТ Р 34. 10‑ 2001) Данный метод полностью аналогичен описанному ранее методу ГОСТ Р 34. 10 94, но возведение в степень заменяется операцией композиции на кривой. Для сообщества пользователей выбирается общая эллиптическая кривая Ep(a, b) и точка G на ней, такая, что G, [2]G , [3]G, . . . , [q]G суть все различные точки множества Ep(a, b), и q = #Ер(а, b), причем [q]G = О. Число точек на кривой, при надлежащем выборе параметров р, а и b, может быть простым числом, #Ер(а, b) = q. В этом случае любая точка (кроме О) являет ся генератором всего множества точек. Длина числа q берется равной 256 бит. Каждый пользователь U выбирает случайное число х. U (секретный ключ), 0 < х. U < q , и вычисляет точку на кривой YU = [х. U]G (открытый ключ). Параметры кривой и список открытых ключей передаются всем пользователям. Защита информации. 08 Системы электронной подписи 25
ЭЦП на эллиптической кривой (ГОСТ Р 34. 10‑ 2001). Алгоритм Чтобы подписать сообщение m пользователь А делает следующее: 1) вычисляет значение хеш функции сообщения h = h(m); 2) выбирает случайно число k , 0 < k < q ; 3) вычисляет P = [k]G = (x, у) ; 4) вычисляет r = х mod q (при r = 0 возвращается к шагу 2); 5) вычисляет s = (k h + r x. А) mod q (при s = 0 возвращается к шагу 2); 6) подписывает сообщение парой чисел (r, s). Для проверки подписанного сообщения (m; r, s) любой пользователь, знающий открытый ключ YA , делает следующее: 1) вычисляет h = h(m); 2) убеждается, что 0 < r, s < q; 3) вычисляет u 1 = s · h 1 mod q и u 2 = r · h l mod q; 4) вычисляет композицию точек на кривой P = [u 1]G + [u 2]YA = (х, у) и если Р = О , отвергает подпись; 5) если х mod q = r, принимает подпись, в противном случае отвергает ее. Защита информации. 08 Системы электронной подписи 26
Эффективная реализация операций. Вычисление m кратной композиции ВХОД: точка Р, число m = (mt mt-1…m 1)2. ВЫХОД: Q = [m]P. 1 Q O; 2 FOR i = t, t-1, …, 1 DO 3 Q [2]Q; 4 IF mi = 1 THEN Q Q + P; 5 RETURN Q. Данный алгоритм требует t удвоений и в среднем t/2 сложений. Пример: Вычислим [21]P. Здесь 21 = (10101)2 , t = 5. Вместо 20 сложений было выполнено 4 удвоения и 3 сложения. i 5 4 3 2 1 mi 1 0 1 : : : Q O, Q [2]Q = [2]P ; Q [2]Q = [4]P, Q [2]Q = [10]P ; Q [2]Q = [20]P, Защита информации. 08 Системы электронной подписи Q Q + P = P ; Q Q + P = [5] P ; Q Q + P = [21] P. 27
Сложение в проективном представлении При вычислении композиции можно избавиться от вычисления инверсии, если в качестве координат использовать рациональные числа, производя вычисления отдельно с числителем и знаменателем. Наиболее выгодным оказалось взвешенное проективное представление координат: Формулы вычисления x 3 и y 3: Защита информации. 08 Системы электронной подписи 28
Сложение в проективном представлении Алгоритм: ВХОД: P 1 = (X 1, Y 1, Z 1), P 2 = (X 2, Y 2, Z 2), P 1, P 2 ≠ O, P 1 ≠ ±P 2 ВЫХОД: P 3 = (X 3, Y 3, Z 3) = P 1 + P 2 λ 1 = X 1 Z 22 λ 2 = X 2 Z 12 λ 3 = λ 2 – λ 1 λ 4 = Y 1 Z 23 λ 5 = Y 2 Z 13 λ 6 = λ 5 – λ 4 λ 7 = λ 1 + λ 2 λ 8 = λ 4 + λ 5 Z 3 = Z 1 Z 2 λ 3 X 3 = λ 62 – λ 7λ 32 λ 9 = λ 7λ 32 – 2 X 3 Y 3 = (λ 9λ 6 – λ 8λ 33) / 2 Защита информации. 08 Системы электронной подписи Пример. P 1 = (5, 1, 1), P 2 = (4, 6, 1) λ 1 = 5 · 1 = 5, λ 2 = 4 · 1 = 4, λ 3 = 4 – 5 = 6, λ 4 = 1 · 1 = 1, λ 5 = 6 · 1 = 6, λ 6 = 6 – 1 = 5, λ 7 = 5 + 4 = 2, λ 8 = 1 + 6 = 0, Z 3 = 1 · 6 = 6, X 3 = 52 – 2 · 62 = 2, λ 9 = 2 · 62 – 2 · 2 = 2 – 4 = 5, Y 3 = (5 · 5 – 0 · 63) / 2 = 25 / 2 = (25+7) / 2 = 16 = 2. P 3 = (2, 2, 6) = (2/62, 2/63) = (2· 6 2, 2· 6 3) = (2· 1, 2· 6) = (2, 5). 29
Удвоение в проективном представлении Формулы вычисления x 3 и y 3: Алгоритм: ВХОД: P 1 = (X 1, Y 1, Z 1), P 1≠ O ВЫХОД: P 3 = (X 3, Y 3, Z 3) = [2]P 1 λ 1 = 3 X 12 + a. Z 14 λ 2 = 4 X 1 Y 12 Z 3 = 2 Y 1 Z 1 X 3 = λ 12 2λ 2 λ 3 = 8 Y 14 Y 3 = λ 1(λ 2 – X 3) – λ 3 Защита информации. 08 Системы электронной подписи 30