Защита и передача информации Сжатие информации Простейшие

Защита и передача информации. Сжатие информации.

Простейшие алгоритмы сжатия информации Цель сжатия – уменьшение количества бит, необходимых для хранения или передачи заданной информации Примеры: программы – архиваторы (Rar, Zip, Arj, GZ и др. ) 2

Пределы сжатия Для формального определения предела сжатия рассматриваем любое информационное сообщение длины n как ◦ Последовательность независимых, одинаково распределенных Д. С. В. Xi или ◦ Как выборки длины n значений одной Д. С. В. X. 3

Пределы сжатия Теорема 1. Среднее количество бит, приходящихся на одно кодируемое значение д. с. в. X, не может быть меньшим, чем энтропия HX этой д. с. в. , т. е. ML(X) ≥ HX для любой д. с. в. X и любого ее кода. Теорема 2. Существует такое кодирование (Шеннона-Фэно), что HX ≥ ML(X) – 1. 4

Основная теорема о кодировании при отсутствии помех С ростом длины сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения. 5

Метод блокирования – для повышения степени сжатия По выбранному значению ε > 0 можно выбрать такое s, что если разбить все сообщение на блоки длиной s (всего будет n/s блоков), то кодированием Шеннона-Фэно таких блоков, рассматриваемых как единицы сообщения, можно сделать среднее количество бит на единицу сообщения большим энтропии менее, чем на ε. Достаточно брать s = 1/ ε. Минимум s по заданному ε может быть гораздо меньшим 1 /ε. 6

Пример блочного кодирования 7

Пример блочного кодирования Длина блока = 2 Имеем д. с. в. 8

Пример блочного кодирования. Длина блока = 3, 4 0. 823 0. 818 9

Все изложенное ранее подразумевало, что рассматриваемые д. с. в. Кодируются только двумя значениями (обычно 0 и 1). Пусть д. с. в. Кодируются m значениями. Тогда для д. с. в. и любого ее кодирования верно, что и 10

Простейшие алгоритмы сжатия информации

Метод Шеннона-Фэно 1. Значения д. с. в. Располагают в порядке убывания их вероятностей. 2. Затем последовательно делят на две части с приблизительно равными вероятностями 3. К коду первой части добавляют 0, а к коду второй – 1 4. И т. д. 12

Пример 1 13

Пример 2 14

Недостатки метода Шеннона-Фэно • С ростом длины сообщения трудоемкость построения кода становится недопустимо большой. • Такое кодирование делает невозможным отправку сообщения по частям, что необходимо для непрерывных процессов передачи данных. • Дополнительный недостаток – необходимость отправки или хранения полученного кода вместе с кодовой таблицей, что снижает эффект от сжатия. 15

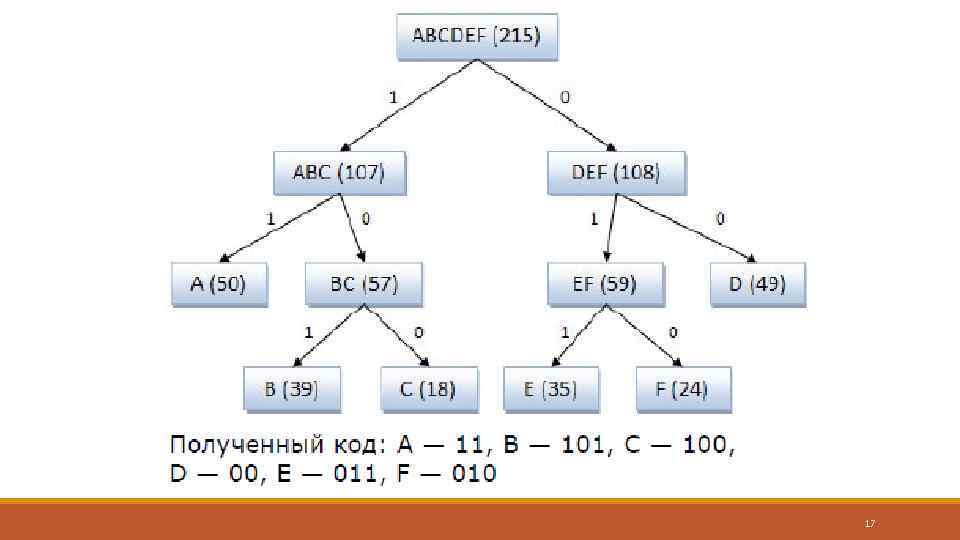
Метод Шеннона-Фэно. Пример построения кодового дерева Исходные символы: • A (частота встречаемости 50); • B (частота встречаемости 39); • C (частота встречаемости 18); • D (частота встречаемости 49); • E (частота встречаемости 35); • F (частота встречаемости 24). 16

17

Метод Хаффмена (1952) • Более практичен и никогда по степени сжатия не уступает методу Шеннона-Фэно, более того, он сжимает максимально плотно. • Код строится при помощи двоичного (бинарного) дерева. Вероятности значений д. с. в. Приписываются его листьям; все дерево строится, опираясь на листья. • Величина, приписанная к узлу дерева, называется весом узла. • Два листа с наименьшими весами создают родительский узел с весом, равным сумме их весов; в дальнейшем этот узел учитывается наравне с оставшимися листьями, а образовавшие его узлы от такого рассмотрения устраняются. • После постройки корня нужно приписать каждой из ветвей, исходящих из родительских узлов, значения 0 или 1. • Код каждого значения д. с. в. – это число, получаемое при обходе ветвей от корня к листу, соответствующему данному значению 18

Пример 1. Построение кода Хаффмена 19

Пример 2. Построение кода Хаффмена 20

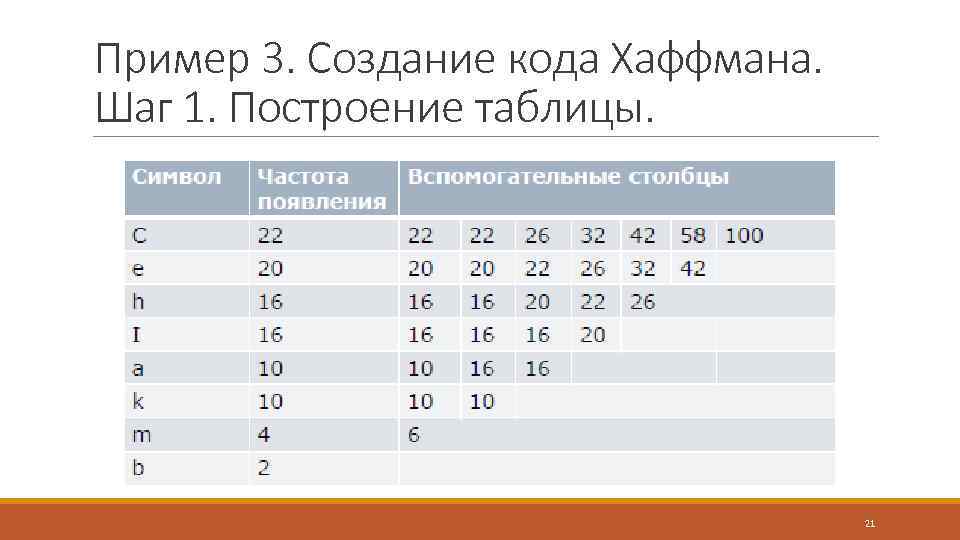Пример 3. Создание кода Хаффмана. Шаг 1. Построение таблицы. 21

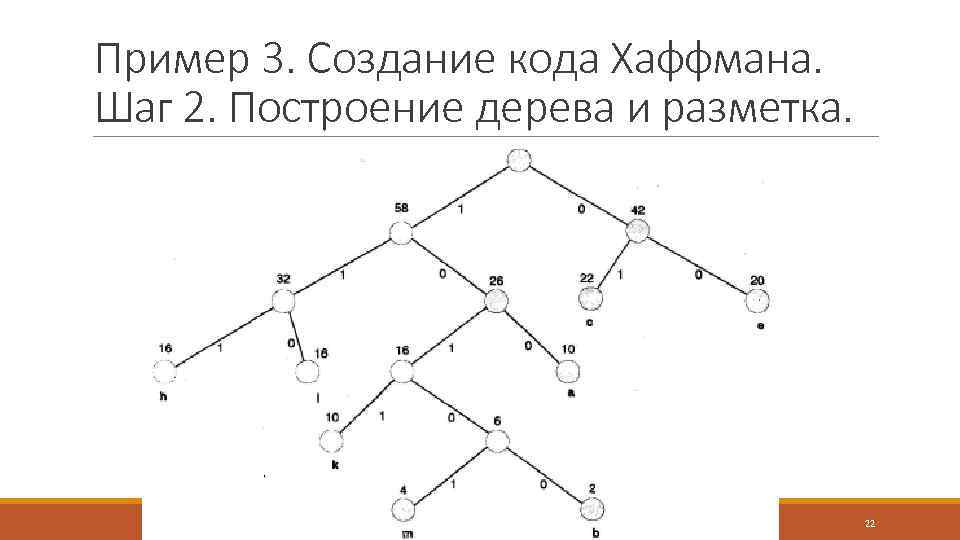Пример 3. Создание кода Хаффмана. Шаг 2. Построение дерева и разметка. 22

Пример 3. Создание кода Хаффмана. Шаг 3. Построение кода по дереву. Двигаясь по кодовому дереву сверху вниз, можем записать для каждого символа соответствующий ему код 23

Задание 24

25

Алгоритмы LZ. Подстановочные или словарно-ориентированные алгоритмы сжатия информации. Методы Лемпела-Зива

Алгоритмы LZ 77 (1977 год) q. Разработан израильским математиками Якобом Зивом (Ziv) и Авраамом Лемпелом (Lempel). q. Одной из причин популярности алгоритмов LZ является их исключительная простота при высокой эффективности сжатия. q. Основная идея LZ 77 состоит в том, что второе и последующие вхождения некоторой строки символов в сообщении заменяются ссылками на ее первое вхождение. q. LZ 77 использует уже просмотренную часть сообщения как словарь. Чтобы добиться сжатия, он пытается заменить очередной фрагмент сообщения на указатель в содержимое словаря. 27

LZ 77 – общий подход q. LZ 77 использует «скользящее» по сообщению окно, разделенное на две неравные части. q. Первая, большая по размеру, является словарем, включает уже просмотренную часть сообщения. q. Вторая, намного меньшая, является буфером, содержащим еще незакодированные символы входного потока. q. Обычно размер окна составляет несколько килобайт, а размер буфера – не более ста байт. Алгоритм пытается найти в словаре (большей части окна) фрагмент, совпадающий с содержимым буфера. q. Алгоритм LZ 77 выдаёт коды, состоящие из трех элементов: q. Смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера; q. Длина этой подстроки; q. Первый символ буфера, следующей за подстрокой. 28

Пример. Закодировать по алгоритму LZ 77 строку «КРАСНАЯ КРАСКА» q. Смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера; q. Длина этой подстроки; q. Первый символ буфера, следующий за подстрокой 29

Длина кода алгоритма LZ 77 q. Длина кода вычисляется следующим образом: длина подстроки не может быть больше размера буфера, а смещение не может быть больше размера словаря – 1. q. Следовательно, длина двоичного кода смещения будет log 2(размер словаря), а длина двоичного кода для длины подстроки будет log 2(размер буфера + 1). q. Символ кодируется 8 битами (например ASCII +). q. В примере длина полученного кода равна 9*(3+3+8)=126 бит, против 14*8=112 бит исходной длины строки. Почему? 30

LZSS. 1982 г. Сторер и Шимански q. Код, выдаваемый LZSS, начинается с однобитного префикса, различающегося собственно код от незакодированного символа. q. Код состоит из пары: смещение и длина, такими же как и для LZ 77. q. В LZSS окно сдвигается ровно на длину найденной подстроки или на 1, если не найдено вхождение подстроки из буфера в словарь. q. Длина подстроки в LZSS всегда больше нуля, поэтому длина двоичного кода для длины подстроки – это log 2(размер буфера + 1). 31

Пример. Закодировать по алгоритму LZSS строку «КРАСНАЯ КРАСКА» 32

Недостатки LZ 77, LZSS q. LZ 77 и LZSS обладают следующими очевидными недостатками: q. Невозможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря; q. Длина подстроки, которую можно закодировать, ограничена размером буфера. q. Если увеличивать размеры словаря и буфера, то это приведет к снижению эффективности кодирования, т. к. с ростом этих величин будут расти и длины кодов для смещения и длины, что сделает коды для коротких подстрок недопустимо большими. Кроме того, резко увеличится время работы алгоритма-кодера. 33

LZ 88 – лишен недостатков LZ 77 q. Не использует «скользящее» окно, он хранит словарь из уже просмотренных фраз. q. При старте алгоритма словарь содержит только пустую строку. q. Алгоритм считывает символы до тех пор, пока накапливаемая подстрока входит целиком в одну из фраз словаря. q. Как только эта строка перестанет соответствовать хотя бы одной фразе словаря, алгоритм генерирует код, состоящий из индекса строки в словаре, которая до последнего введенного символа содержала входную строку, и символа, нарушившего совпадение. q. Затем в словарь добавляется введенная подстрока. q. Если словарь уже заполнен, то из него предварительно удаляют менее всех используемую в сравнениях фразу. 34

Пример. Закодировать по алгоритму LZ 88 строку «КРАСНАЯ КРАСКА» , используя словарь длиной 16 фраз. 35

Длина кода LZ 88 q. Ключевым для размера получаемых кодов является размер словаря во фразах, потому что каждый код при кодировании по методу LZ 88 содержит номер фразы в словаре. q. Из последнего следует, что эти коды имеют постоянную длину, равную log 2(размер словаря+ 8). (8 – это количество бит в байт-коде расширенного ASCII). q. В примере: q. Указатель на любую фразу словаря из 16 фраз – это число от 0 до 15, для его кодирования достаточно 4 бит. q. Длина полученного кода равна 10*(4+8) = 120 бит. 36

LZ 77 и LZSS обладают следующими недостатками очевидными недостатками: ◦ Невозможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря; ◦ Длина подстроки, которую можно закодировать, ограничена размером буфера. 37

Алгоритм LZ (1978 год) q. Алгоритм Лемпеля – Зива – Велча (Lempel – Ziv – Welch, LZW) q. Универсальный алгоритм сжатия данных без потерь, созданный Абрахамом Лемпелем, Якобом Зивом и Терри Велчем. q. Опубликован Велчем, как улучшение алгоритма LZ 78 (Лемпель и Зив, 1978) 38

Алгоритм LZW. 1984 г. – модификация LZ 78 Уэлчем. q. Шаг 1. Инициализация словаря всеми возможными односимвольными фразами (обычно 256 символами ASCII +). Инициализация входной фразы W первым символом сообщения. q. Шаг 2. Считать очередной символ K из сообщения. q. Шаг 3. Если КОНЕЦ_СООБЩЕНИЯ q. Выдать код для W q. Конец q. Если фраза w. K уже есть в словаре q. Присвоить входной фразе значение w. K q. Перейти к Шагу 2 q. Иначе q. Выдать код w q. Добавить w. K в словарь q. Присвоить входной фразе значение K q. Перейти к шагу 2 39

Пример. Закодировать по алгоритму LZW строку «КРАСНАЯ КРАСКА» . Размер словаря – 500 фраз. q. LZW-коды имеют постоянную длину равную log 2(размер словаря) q. Длина полученного кода равна 12*9 = 108 битам q. При переполнении словаря из него удаляют либо наиболее редко используемую фразу, либо все фразы, отличающиеся от одиночного символа. 40

Об LZW q. Алгоритм допускает быструю реализацию, но не обязательно оптимален, т. к. не проводит никакого анализа входных данных. q. Алгоритм реализован в программе compress, которая стала стандартной утилитой Unix-систем в 1986 году. q. В 1987 году алгоритм стал частью стандарта на формат изображений GIF. Он также может (опционально) использоваться в формате TIFF. q. В настоящее время, алгоритм содержится в стандарте PDF. 41

Задание 42