Скачать презентацию Запись числа в десятичной системе счисления Лекция 2 Скачать презентацию Запись числа в десятичной системе счисления Лекция 2

2 курс лекция 2 вариант.ppt

  • Количество слайдов: 34

Запись числа в десятичной системе счисления Лекция 2 Запись числа в десятичной системе счисления Лекция 2

Система счисления – язык для наименования и записи чисел и выполенения действий над Система счисления – язык для наименования и записи чисел и выполенения действий над ними

• Непозиционные системы счисления характеризуются тем, что каждый знак всегда обозначает одно и • Непозиционные системы счисления характеризуются тем, что каждый знак всегда обозначает одно и тоже число. • Например, в римской системе счисления: • I – один • III – один да один, да один равно три • IV, VIII, IX, XII, CXXI, MMXI

• В России до XVII в. Использовалась славянская непозиционная нумерация. • Числа в • В России до XVII в. Использовалась славянская непозиционная нумерация. • Числа в такой нумерации обозначались буквами славянского алфавита, над которыми ставили особый знак – титло.

В России славянская нумерация сохранилась до конца XVII в. При Петре I возобладала так В России славянская нумерация сохранилась до конца XVII в. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранялась только в богослужебных книгах.

• В позиционных системах один и тот же знак может обозначать различные числа • В позиционных системах один и тот же знак может обозначать различные числа а зависимости от места(позиции) • Например: 1111, 343434, 2342342

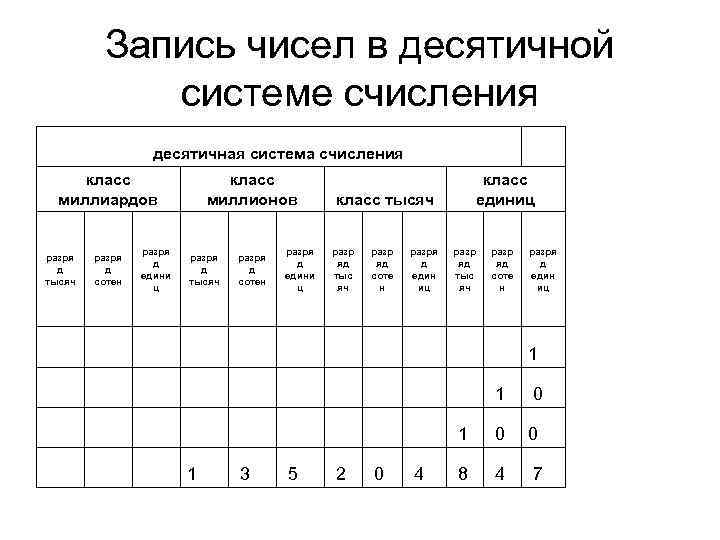Запись чисел в десятичной системе счисления десятичная система счисления класс миллиардов класс миллионов класс Запись чисел в десятичной системе счисления десятичная система счисления класс миллиардов класс миллионов класс единиц класс тысяч разря д сотен разря д едини ц разря д тысяч разря д сотен разря д едини ц разр яд тыс яч разр яд соте н разря д един иц 1 0 0 1 3 5 2 0 4 8 4 7

Правила нумерации • Правило прочтения чисел: • 1. Раздели число на классы справа на- Правила нумерации • Правило прочтения чисел: • 1. Раздели число на классы справа на- лево. Каждый класс должен содержать три разряда. Только старший класс может быть неполным. • 2. Сначала называем разряды старшего класса и название класса. Затем называем разряды следующего класса и т. д.

Правило записи числа • 1. Записываем цифры старшего класса. • 2. Затем, цифры младших Правило записи числа • 1. Записываем цифры старшего класса. • 2. Затем, цифры младших классов, помня о том, каждый следующий класс должен быть полным.

• Например: • Три миллиона двести сорок пять тысяч шестнадцать. 3 _ _ • Например: • Три миллиона двести сорок пять тысяч шестнадцать. 3 _ _ _ 3 245 016

• Основа записи чисел в десятичной системе • Основа записи чисел в десятичной системе

Определение. • Десятичной записью натурального числа х называется представление в виде: где коэффициенты аi Определение. • Десятичной записью натурального числа х называется представление в виде: где коэффициенты аi принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и аn ≠ 0

Теорема 1 • Любое натуральное число х можно представить в виде суммы разрядных слагаемых. Теорема 1 • Любое натуральное число х можно представить в виде суммы разрядных слагаемых.

Доказательство существования записи числа. • Пусть тогда Разделим число x : Имеем где Доказательство существования записи числа. • Пусть тогда Разделим число x : Имеем где

• Продолжим деление. где В результате имеем Процесс деления конечен, так как Последний • Продолжим деление. где В результате имеем Процесс деления конечен, так как Последний неравный нулю остаток обозначим a 0. ч. т. д.

Доказательство единственности. • Старшая степень числа x определяется однозначно. • Деление с остатком также Доказательство единственности. • Старшая степень числа x определяется однозначно. • Деление с остатком также однозначно. • Следовательно, представление числа в виде суммы разрядных слагаемых также однозначно.

Сравнение натуральных чисел • Теорема 2: Пусть x и y – натуральные числа, запись Сравнение натуральных чисел • Теорема 2: Пусть x и y – натуральные числа, запись которых дана в десятичной системе счисления:

• Тогда число x меньше числа у (x<y), если выполнено одно из условий: • Тогда число x меньше числа у (x

• Например: • 1. 34 < 341 • 2. 628 < 828 • • Например: • 1. 34 < 341 • 2. 628 < 828 • 3. 65734 < 65794

Доказательство • 1) Если ; то Следовательно x<y Доказательство • 1) Если ; то Следовательно x

• 2) Если n=m, но то тогда Значит, Следовательно x<y • 2) Если n=m, но то тогда Значит, Следовательно x

Например: • 1) x=54267; y=5426 x= 345; y= 2314 2) a=6789; b=5789 a=1245; b=3245 Например: • 1) x=54267; y=5426 x= 345; y= 2314 2) a=6789; b=5789 a=1245; b=3245 3) m=3456; n=3421 m=1454; n=1458

Алгоритм сложения • • • x=345; y=598. Найдем сумму чисел х+y: 345+ 598= (300+40+5)+(500+90+8)= Алгоритм сложения • • • x=345; y=598. Найдем сумму чисел х+y: 345+ 598= (300+40+5)+(500+90+8)= (300+500)+(40+90)+(5+8)= 800+13= 800+(100+30)+(10+3)= (800+100)+(30+10)+3 =900+40+3=943

В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты: 1. Способ записи чисел В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты: 1. Способ записи чисел в десятичной системе счисления; 2. Коммутативный и ассоциативный законы сложения натуральных чисел; 3. Дистрибутивный закон умножения относительно сложения; 4. Таблица сложения однозначных чисел.

Рассмотрим алгоритм сложения многозначных чисел в общем виде (для чисел x и y) • Рассмотрим алгоритм сложения многозначных чисел в общем виде (для чисел x и y) • Пусть числа x и y в общем виде:

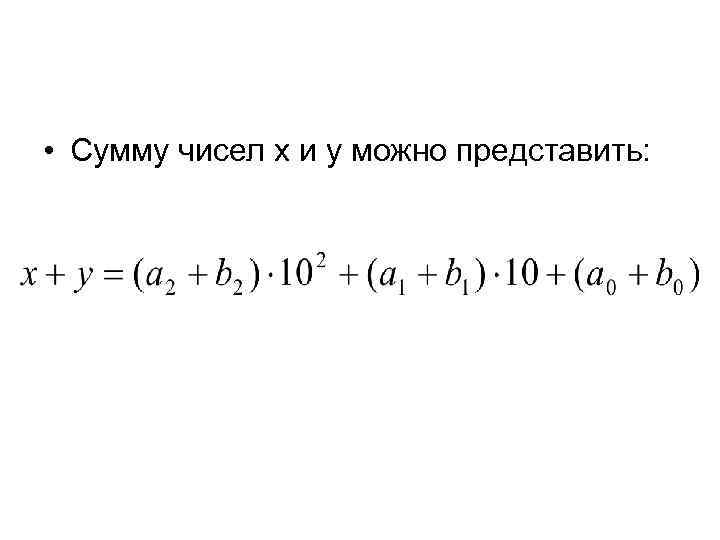• Сумму чисел x и y можно представить: • Сумму чисел x и y можно представить:

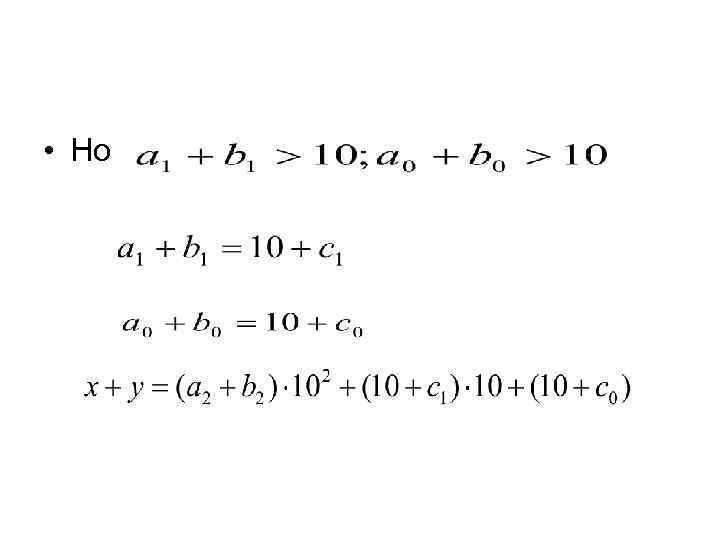• Но • Но

• Применив дистрибутивный закон, имеем: Применив дистрибутивный закон для 1 и 2 , • Применив дистрибутивный закон, имеем: Применив дистрибутивный закон для 1 и 2 , а так же для 3 и 4 слагаемых, имеем:

• Так как и то Тем самым получена десятичная запись числа • Так как и то Тем самым получена десятичная запись числа

Алгоритм сложения натуральных чисел, записанных в десятичной системе счисления 1. Записывают второе слагаемое Алгоритм сложения натуральных чисел, записанных в десятичной системе счисления 1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом. 2. Складывают единицы первого разряда. Если сумма меньше 10, записывают ее в разряде единиц ответа и переходят к следующему разряду (десятков)

3. Если сумма единиц больше или равна 10, то представляют ее в виде где 3. Если сумма единиц больше или равна 10, то представляют ее в виде где однозначное число

4. Повторяют те же действия с десятками, потом с сотнями и т. д. Процесс 4. Повторяют те же действия с десятками, потом с сотнями и т. д. Процесс этот конечен.

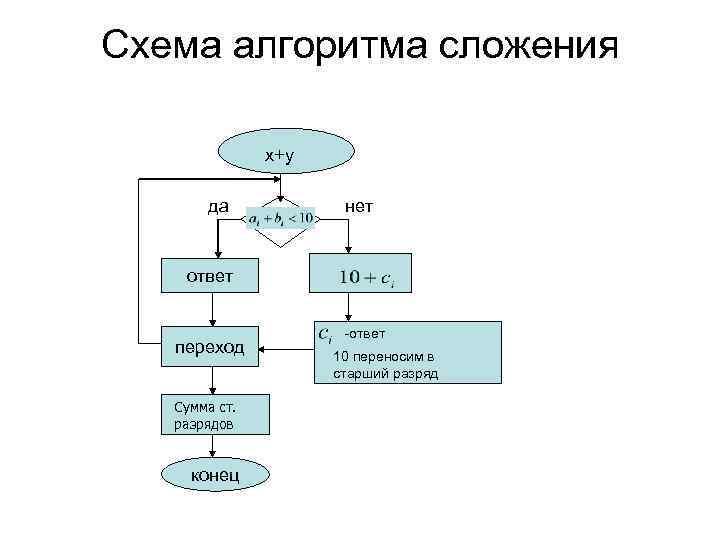Схема алгоритма сложения x+y да нет ответ переход Сумма ст. разрядов конец -ответ 10 Схема алгоритма сложения x+y да нет ответ переход Сумма ст. разрядов конец -ответ 10 переносим в старший разряд

Спасибо за внимание! Спасибо за внимание!