занятие_8_однофакт_дисп_ан_2013.ppt
- Количество слайдов: 112
 ЗАНЯТИЕ 8 ТЕМА: ДИСПЕРСИОННЫЙ АНАЛИЗ ( ANOVA ). ПОНЯТИЕ ОБ ОРТОГОНАЛЬНОМ И НЕОРТОГОНАЛЬНОМ КОМПЛЕКСАХ. ПРЕДПОСЫЛКИ, ЗАДАЧИ И ТЕХНИКА ПРОВЕДЕНИЯ ОДНО- И ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА. КРИТЕРИЙ БАРТЛЕТА. СИЛА ВЛИЯНИЯ ФАКТОРА.
ЗАНЯТИЕ 8 ТЕМА: ДИСПЕРСИОННЫЙ АНАЛИЗ ( ANOVA ). ПОНЯТИЕ ОБ ОРТОГОНАЛЬНОМ И НЕОРТОГОНАЛЬНОМ КОМПЛЕКСАХ. ПРЕДПОСЫЛКИ, ЗАДАЧИ И ТЕХНИКА ПРОВЕДЕНИЯ ОДНО- И ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА. КРИТЕРИЙ БАРТЛЕТА. СИЛА ВЛИЯНИЯ ФАКТОРА.
 Анализ статистических связей • Дисперсионный анализ • Корреляционный анализ • Регрессионный анализ Изучение закономерных проявлений в поведении варьирующих признаков статистических комплексов и роли остатков - случайного варьирования
Анализ статистических связей • Дисперсионный анализ • Корреляционный анализ • Регрессионный анализ Изучение закономерных проявлений в поведении варьирующих признаков статистических комплексов и роли остатков - случайного варьирования
 • Дисперсионный анализ Основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты. Сравнивая их друг с другом с помощью fкритерия, можно определить, какую долю общей вариации изучаемого признака, обуславливает действие на него организованных и случайных воздействий.
• Дисперсионный анализ Основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты. Сравнивая их друг с другом с помощью fкритерия, можно определить, какую долю общей вариации изучаемого признака, обуславливает действие на него организованных и случайных воздействий.
 • Дисперсионный анализ Основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты. Сравнивая их друг с другом с помощью fкритерия, можно определить, какую долю общей вариации изучаемого признака, обуславливает действие на него организованных и случайных воздействий. Организованные воздействия обычно трактуются как факторы
• Дисперсионный анализ Основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты. Сравнивая их друг с другом с помощью fкритерия, можно определить, какую долю общей вариации изучаемого признака, обуславливает действие на него организованных и случайных воздействий. Организованные воздействия обычно трактуются как факторы
 1. Есть m-выборок, полученных из одной генеральной по определенному порядку статистический комплекс. 2. Общяя вариация признака - сумма квадратов отклонений отдельных вариант от средней арифметической
1. Есть m-выборок, полученных из одной генеральной по определенному порядку статистический комплекс. 2. Общяя вариация признака - сумма квадратов отклонений отдельных вариант от средней арифметической
 1. Есть m-выборок, полученных из одной генеральной по определенному порядку статистический комплекс. 2. Общяя вариация признака - сумма квадратов отклонений отдельных вариант от средней арифметической Её можно разложить на доли: • одна отражает влияние на признак учитываемого в опыте фактора (или факторов) • другая определяется влиянием на тот же признак неучитываемых (случайных) причин.
1. Есть m-выборок, полученных из одной генеральной по определенному порядку статистический комплекс. 2. Общяя вариация признака - сумма квадратов отклонений отдельных вариант от средней арифметической Её можно разложить на доли: • одна отражает влияние на признак учитываемого в опыте фактора (или факторов) • другая определяется влиянием на тот же признак неучитываемых (случайных) причин.
 1. Есть m-выборок, полученных из одной генеральной по определенному порядку статистический комплекс. 2. Общяя вариация признака - сумма квадратов отклонений отдельных вариант от средней арифметической Её можно разложить на доли: • одна отражает влияние на признак учитываемого в опыте фактора (или факторов) • другая определяется влиянием на тот же признак неучитываемых (случайных) причин.
1. Есть m-выборок, полученных из одной генеральной по определенному порядку статистический комплекс. 2. Общяя вариация признака - сумма квадратов отклонений отдельных вариант от средней арифметической Её можно разложить на доли: • одна отражает влияние на признак учитываемого в опыте фактора (или факторов) • другая определяется влиянием на тот же признак неучитываемых (случайных) причин.
 ОСНОВНЫЕ ПРЕДПОСЫЛКИ КОРРЕКТНОСТИ ПРОЦЕДУРЫ ДИСПЕРСИОННОГО АНАЛИЗА: 1. Случайность выборок (независимость вариант каждой выборки от вариант других выборок, т. е. отсутствие корреляций внутри комплекса); 2. Нормальное распределение вариант в каждой из сравниваемых выборок; ПРИ N<30 НЕОБХОДИМО ПРЕОБРАЗОВАНИЕ ВАРИАНТ!!!. 3. Равенство дисперсий сравниваемых отдельных выборок
ОСНОВНЫЕ ПРЕДПОСЫЛКИ КОРРЕКТНОСТИ ПРОЦЕДУРЫ ДИСПЕРСИОННОГО АНАЛИЗА: 1. Случайность выборок (независимость вариант каждой выборки от вариант других выборок, т. е. отсутствие корреляций внутри комплекса); 2. Нормальное распределение вариант в каждой из сравниваемых выборок; ПРИ N<30 НЕОБХОДИМО ПРЕОБРАЗОВАНИЕ ВАРИАНТ!!!. 3. Равенство дисперсий сравниваемых отдельных выборок
 РАВЕНСТВО ДИСПЕРСИЙ Проверка гипотезы о равенстве выборочных дисперсий с помощью критерия Бартлета УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ.
РАВЕНСТВО ДИСПЕРСИЙ Проверка гипотезы о равенстве выборочных дисперсий с помощью критерия Бартлета УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ.
 РАВЕНСТВО ДИСПЕРСИЙ Проверка гипотезы о равенстве выборочных дисперсий с помощью критерия Бартлета УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны
РАВЕНСТВО ДИСПЕРСИЙ Проверка гипотезы о равенстве выборочных дисперсий с помощью критерия Бартлета УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны
 РАВЕНСТВО ДИСПЕРСИЙ Проверка гипотезы о равенстве выборочных дисперсий с помощью критерия Бартлета УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны Для проверки нулевой гипотезы строим односторонний критерий
РАВЕНСТВО ДИСПЕРСИЙ Проверка гипотезы о равенстве выборочных дисперсий с помощью критерия Бартлета УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны Для проверки нулевой гипотезы строим односторонний критерий
 ПРОВЕРЯЕТСЯ УСЛОВИЕ: m - количество выборок Принимается нулевая гипотеза
ПРОВЕРЯЕТСЯ УСЛОВИЕ: m - количество выборок Принимается нулевая гипотеза
 ОСНОВНЫЕ ПРЕДПОСЫЛКИ КОРРЕКТНОСТИ ПРОЦЕДУРЫ ДИСПЕРСИОННОГО АНАЛИЗА: 4. НЕЗАВИСИМОСТЬ СРЕДНЕЙ ОТ ДИСПЕРСИИ В ВЫБОРКАХ КОМПЛЕКСА 5. АДДИТИВНОСТЬ КОМПОНЕНТ ВАРИАНСЫ КОМПЛЕКСА. АДДИТИВНОСТЬ МОДЕЛИ -слагаемость компонент общей вариансы статистического комплекса, обусловленных главными эффектами воздействий. АДДИТИВНЫЙ ЭФФЕКТ - отсутствие взаимодействия.
ОСНОВНЫЕ ПРЕДПОСЫЛКИ КОРРЕКТНОСТИ ПРОЦЕДУРЫ ДИСПЕРСИОННОГО АНАЛИЗА: 4. НЕЗАВИСИМОСТЬ СРЕДНЕЙ ОТ ДИСПЕРСИИ В ВЫБОРКАХ КОМПЛЕКСА 5. АДДИТИВНОСТЬ КОМПОНЕНТ ВАРИАНСЫ КОМПЛЕКСА. АДДИТИВНОСТЬ МОДЕЛИ -слагаемость компонент общей вариансы статистического комплекса, обусловленных главными эффектами воздействий. АДДИТИВНЫЙ ЭФФЕКТ - отсутствие взаимодействия.
 По условиям формирования статистические комплексы могут быть: ОДНО-, ДВУХ-, ТРЕХ - И БОЛЕЕ- ФАКТОРНЫМИ. Один организованный фактор: (4 градации по фактору Однофакторный дисперсионный комплекс А 1 А 2 ni ni А 3 ni А 4 ni А: а =4)
По условиям формирования статистические комплексы могут быть: ОДНО-, ДВУХ-, ТРЕХ - И БОЛЕЕ- ФАКТОРНЫМИ. Один организованный фактор: (4 градации по фактору Однофакторный дисперсионный комплекс А 1 А 2 ni ni А 3 ni А 4 ni А: а =4)
 По условиям формирования статистические комплексы могут быть: ОДНО-, ДВУХ-, ТРЕХ - И БОЛЕЕ- ФАКТОРНЫМИ. Один организованный фактор: (4 градации по фактору Однофакторный дисперсионный комплекс А 1 А 2 ni ni А 3 ni А: а =4) А 4 ni Два организованных фактора (Двухфакторный дисперсионный комплекс: (4 градации по фактору А: а =4; 2 градации по фактору В: b=2) А 1 А 2 А 3 А 4 В 1 ni ni В 2 ni ni А и B - градации организованных воздействий
По условиям формирования статистические комплексы могут быть: ОДНО-, ДВУХ-, ТРЕХ - И БОЛЕЕ- ФАКТОРНЫМИ. Один организованный фактор: (4 градации по фактору Однофакторный дисперсионный комплекс А 1 А 2 ni ni А 3 ni А: а =4) А 4 ni Два организованных фактора (Двухфакторный дисперсионный комплекс: (4 градации по фактору А: а =4; 2 градации по фактору В: b=2) А 1 А 2 А 3 А 4 В 1 ni ni В 2 ni ni А и B - градации организованных воздействий
 По условиям формирования статистические комплексы (или дисперсионные) могут быть: ОРТОГОНАЛЬНЫМИ и НЕОРТОГОНАЛЬНЫМИ число вариант в каждой ячейке или по градациям каждого из факторов выровнено. ПРОПОРЦИОНАЛЬНЫЙ КОМПЛЕКС 2 3 4 3 5 7 3 3 3 или 5 5 5 4 3 2 7 5 3 РАВНОМЕРНЫЙ КОМПЛЕКС 3 3 3 или 3 3 3 5 5 5 5 5 НЕРАВНОМЕРНЫЙ КОМПЛЕКС 3 5 9 5 7 4 или 4 2 2 2 3 8 7 9 8
По условиям формирования статистические комплексы (или дисперсионные) могут быть: ОРТОГОНАЛЬНЫМИ и НЕОРТОГОНАЛЬНЫМИ число вариант в каждой ячейке или по градациям каждого из факторов выровнено. ПРОПОРЦИОНАЛЬНЫЙ КОМПЛЕКС 2 3 4 3 5 7 3 3 3 или 5 5 5 4 3 2 7 5 3 РАВНОМЕРНЫЙ КОМПЛЕКС 3 3 3 или 3 3 3 5 5 5 5 5 НЕРАВНОМЕРНЫЙ КОМПЛЕКС 3 5 9 5 7 4 или 4 2 2 2 3 8 7 9 8
 НЕПРЕМЕННЫМ УСЛОВИЯМИ КОРРЕКТНОГО АНАЛИЗА ДИСПЕРСИОННОГО КОМПЛЕКСА ЯВЛЯЮТСЯ: § заполнение всех ячеек комплекса вариантами; § число вариант в ячейке должно быть не ниже 2.
НЕПРЕМЕННЫМ УСЛОВИЯМИ КОРРЕКТНОГО АНАЛИЗА ДИСПЕРСИОННОГО КОМПЛЕКСА ЯВЛЯЮТСЯ: § заполнение всех ячеек комплекса вариантами; § число вариант в ячейке должно быть не ниже 2.
 ТЕХНИКА ПРОВЕДЕНИЯ ДИСПЕРСИОННОГО АНАЛИЗА АНАЛИЗ РАВНОМЕРНОГО КОМПЛЕКСА т. е. различия между выборочными средними случайны средняя выборочная хотя бы ОДНОЙ ВЫБОРКИ отличается от генеральной средней.
ТЕХНИКА ПРОВЕДЕНИЯ ДИСПЕРСИОННОГО АНАЛИЗА АНАЛИЗ РАВНОМЕРНОГО КОМПЛЕКСА т. е. различия между выборочными средними случайны средняя выборочная хотя бы ОДНОЙ ВЫБОРКИ отличается от генеральной средней.
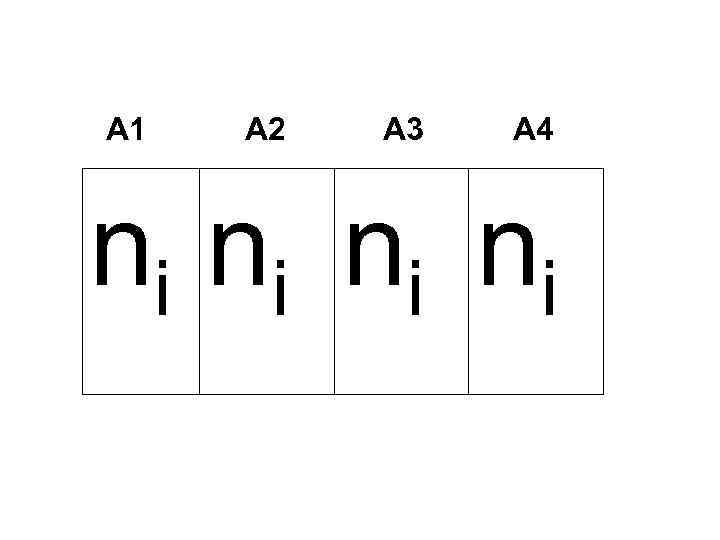 А 1 А 2 А 3 А 4 ni ni
А 1 А 2 А 3 А 4 ni ni
 ТЕХНИКА ПРОВЕДЕНИЯ ДИСПЕРСИОННОГО АНАЛИЗА АНАЛИЗ РАВНОМЕРНОГО КОМПЛЕКСА т. е. различия между выборочными средними случайны средняя выборочная хотя бы ОДНОЙ ВЫБОРКИ отличается от генеральной средней. ОДНОФАКТОРНЫЙ АНАЛИЗ SSA- межгрупповая сумма квадратов (ДЕВИАТА) обусловлена различиями между выборками; SSW - внутригрупповая (остаточная, необъясненная) сумма квадратов, обусловленная варьированием признака внутри выборок.
ТЕХНИКА ПРОВЕДЕНИЯ ДИСПЕРСИОННОГО АНАЛИЗА АНАЛИЗ РАВНОМЕРНОГО КОМПЛЕКСА т. е. различия между выборочными средними случайны средняя выборочная хотя бы ОДНОЙ ВЫБОРКИ отличается от генеральной средней. ОДНОФАКТОРНЫЙ АНАЛИЗ SSA- межгрупповая сумма квадратов (ДЕВИАТА) обусловлена различиями между выборками; SSW - внутригрупповая (остаточная, необъясненная) сумма квадратов, обусловленная варьированием признака внутри выборок.
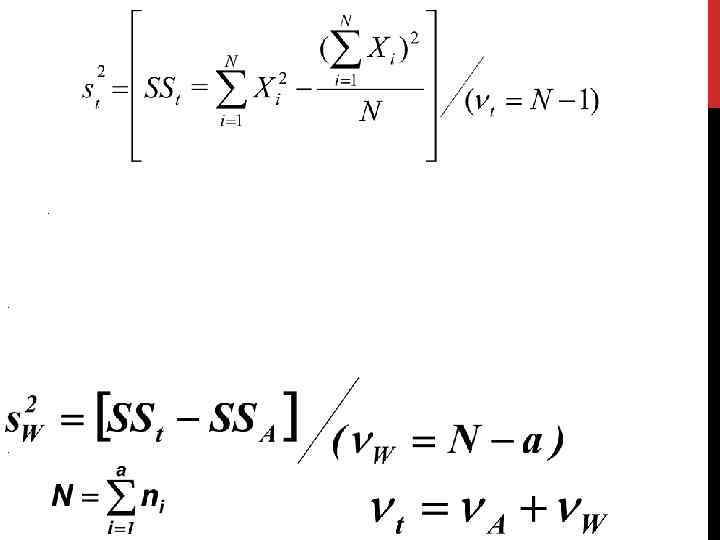 . . .
. . .
 ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА: Нулевая гипотеза сохраняется, если F Fкрит ( , А, W).
ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА: Нулевая гипотеза сохраняется, если F Fкрит ( , А, W).
 ВОЗМОЖНЫЕ ВЫВОДЫ • Влияние организованного фактора достоверно. Это означает, что средняя по крайней мере одной из сравниваемых выборок достоверно отличается от остальных. В этом случае остается только определить – какая? или найти общий тренд. • Влияние организованного фактора не достоверно. Такая ситуация вполне реальна. В данном случае при проведении дисперсионного анализа необходимо до конца соблюдать правила игры: следует признать случайным отклонения вариант от средней для всего статистического комплекса и отнести их к одной генеральной совокупности - т. е. объединить все сравниваемые выборки.
ВОЗМОЖНЫЕ ВЫВОДЫ • Влияние организованного фактора достоверно. Это означает, что средняя по крайней мере одной из сравниваемых выборок достоверно отличается от остальных. В этом случае остается только определить – какая? или найти общий тренд. • Влияние организованного фактора не достоверно. Такая ситуация вполне реальна. В данном случае при проведении дисперсионного анализа необходимо до конца соблюдать правила игры: следует признать случайным отклонения вариант от средней для всего статистического комплекса и отнести их к одной генеральной совокупности - т. е. объединить все сравниваемые выборки.
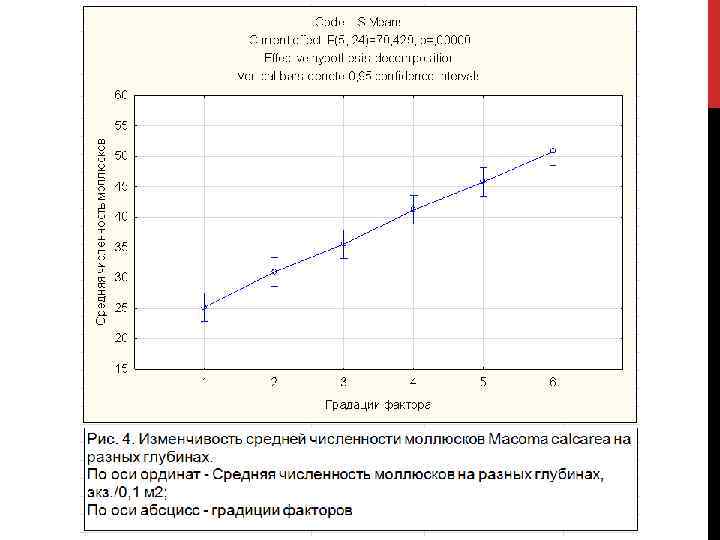
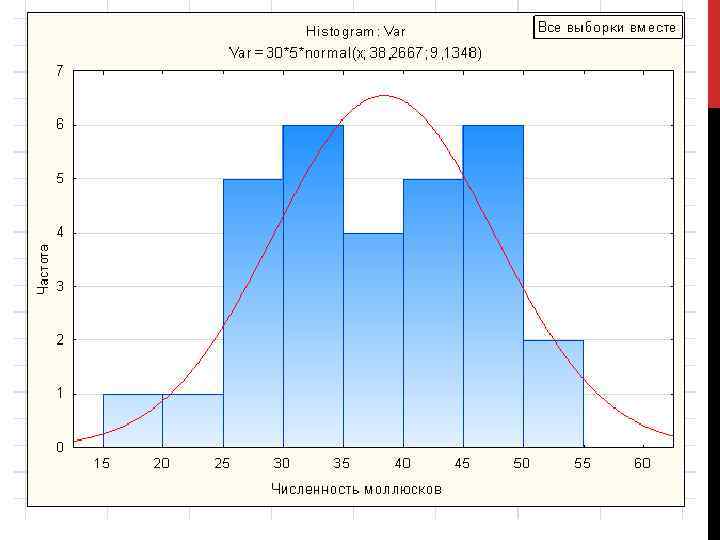
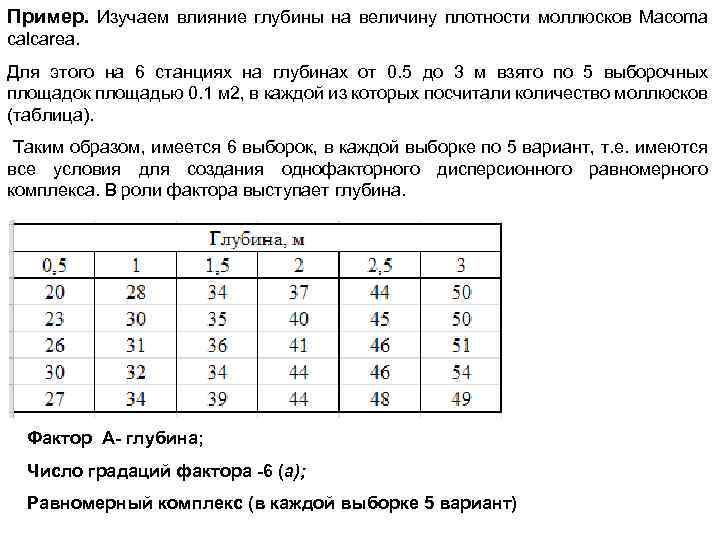 Пример. Изучаем влияние глубины на величину плотности моллюсков Macoma calcarea. Для этого на 6 станциях на глубинах от 0. 5 до 3 м взято по 5 выборочных площадок площадью 0. 1 м 2, в каждой из которых посчитали количество моллюсков (таблица). Таким образом, имеется 6 выборок, в каждой выборке по 5 вариант, т. е. имеются все условия для создания однофакторного дисперсионного равномерного комплекса. В роли фактора выступает глубина. Фактор А- глубина; Число градаций фактора -6 (a); Равномерный комплекс (в каждой выборке 5 вариант)
Пример. Изучаем влияние глубины на величину плотности моллюсков Macoma calcarea. Для этого на 6 станциях на глубинах от 0. 5 до 3 м взято по 5 выборочных площадок площадью 0. 1 м 2, в каждой из которых посчитали количество моллюсков (таблица). Таким образом, имеется 6 выборок, в каждой выборке по 5 вариант, т. е. имеются все условия для создания однофакторного дисперсионного равномерного комплекса. В роли фактора выступает глубина. Фактор А- глубина; Число градаций фактора -6 (a); Равномерный комплекс (в каждой выборке 5 вариант)
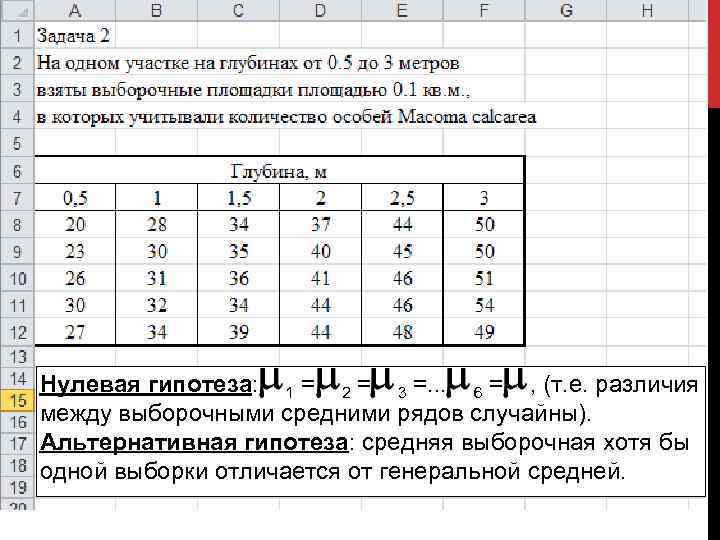 Нулевая гипотеза: 1 = 2 = 3 =. . . 6 = , (т. е. различия между выборочными средними рядов случайны). Альтернативная гипотеза: средняя выборочная хотя бы одной выборки отличается от генеральной средней.
Нулевая гипотеза: 1 = 2 = 3 =. . . 6 = , (т. е. различия между выборочными средними рядов случайны). Альтернативная гипотеза: средняя выборочная хотя бы одной выборки отличается от генеральной средней.
 АНАЛИЗ КОМПЛЕКСА ДАННЫХ НА СООТВЕТСТВИЕ УСЛОВИЯМ ПРОВЕДЕНИЯ ДИСПЕРСИОННОГО АНАЛИЗА Допустим: ü нормальность распределения вариант в каждой из сравниваемых выборок ü случайность выборок ü независимость средних от дисперсий в выборках комплекса. Оценим значимость различий дисперсий отдельных выборок с помощью критерия Бартлета.
АНАЛИЗ КОМПЛЕКСА ДАННЫХ НА СООТВЕТСТВИЕ УСЛОВИЯМ ПРОВЕДЕНИЯ ДИСПЕРСИОННОГО АНАЛИЗА Допустим: ü нормальность распределения вариант в каждой из сравниваемых выборок ü случайность выборок ü независимость средних от дисперсий в выборках комплекса. Оценим значимость различий дисперсий отдельных выборок с помощью критерия Бартлета.
 ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЫБОРОЧНЫХ ДИСПЕРСИЙ С ПОМОЩЬЮ КРИТЕРИЯ БАРТЛЕТА Нулевая гипотеза -… Альтернативная гипотеза -….
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЫБОРОЧНЫХ ДИСПЕРСИЙ С ПОМОЩЬЮ КРИТЕРИЯ БАРТЛЕТА Нулевая гипотеза -… Альтернативная гипотеза -….
 ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЫБОРОЧНЫХ ДИСПЕРСИЙ С ПОМОЩЬЮ КРИТЕРИЯ БАРТЛЕТА Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны. УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ.
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЫБОРОЧНЫХ ДИСПЕРСИЙ С ПОМОЩЬЮ КРИТЕРИЯ БАРТЛЕТА Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны. УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ.
 ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЫБОРОЧНЫХ ДИСПЕРСИЙ С ПОМОЩЬЮ КРИТЕРИЯ БАРТЛЕТА Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны. УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. Для проверки нулевой гипотезы строим односторонний критерий
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЫБОРОЧНЫХ ДИСПЕРСИЙ С ПОМОЩЬЮ КРИТЕРИЯ БАРТЛЕТА Нулевая гипотеза - выборки относятся к одной генеральной совокупности и, следовательно, наблюдаемые различия между выборочными вариансами случайны Альтернативная гипотеза - наблюдаемые различия между выборочными дисперсиями неслучайны. УСЛОВИЕ КОРРЕКТНОСТИ ПРОЦЕДУРЫ: СЛУЧАЙНОСТЬ ВАРИАНТ ВЫБОРОК И НОРМАЛЬНОСТЬ ИХ РАСПРЕДЕЛЕНИЯ. Для проверки нулевой гипотезы строим односторонний критерий
 ПРОВЕРЯЕТСЯ УСЛОВИЕ: m - количество выборок Принимается нулевая гипотеза
ПРОВЕРЯЕТСЯ УСЛОВИЕ: m - количество выборок Принимается нулевая гипотеза
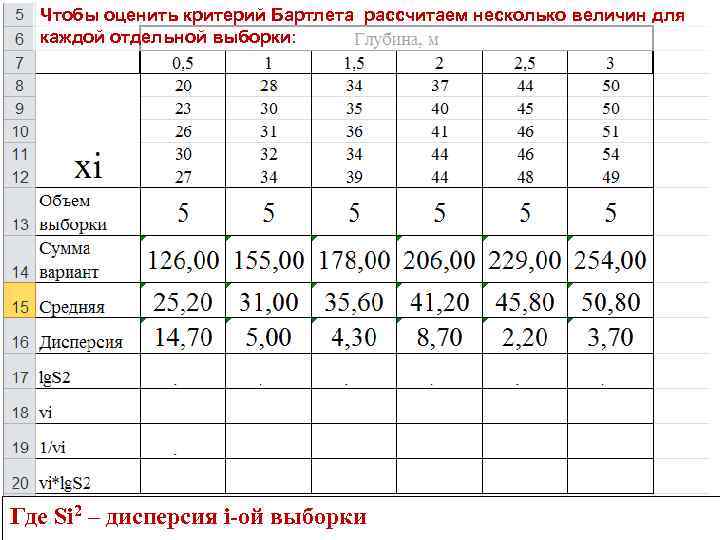
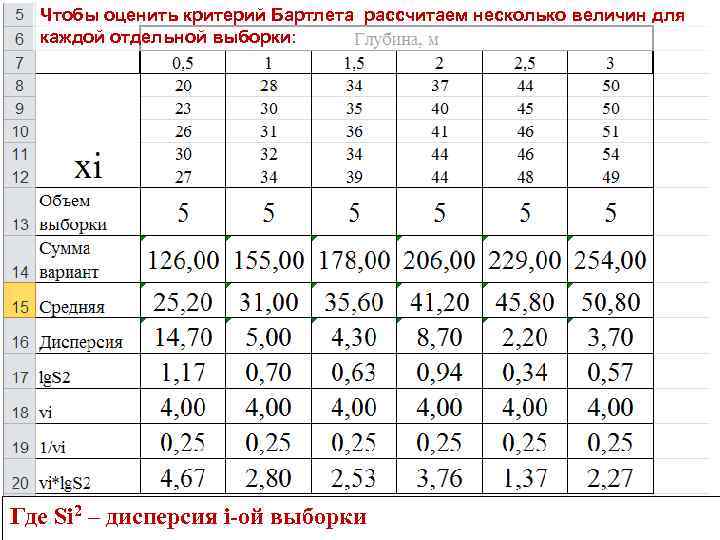
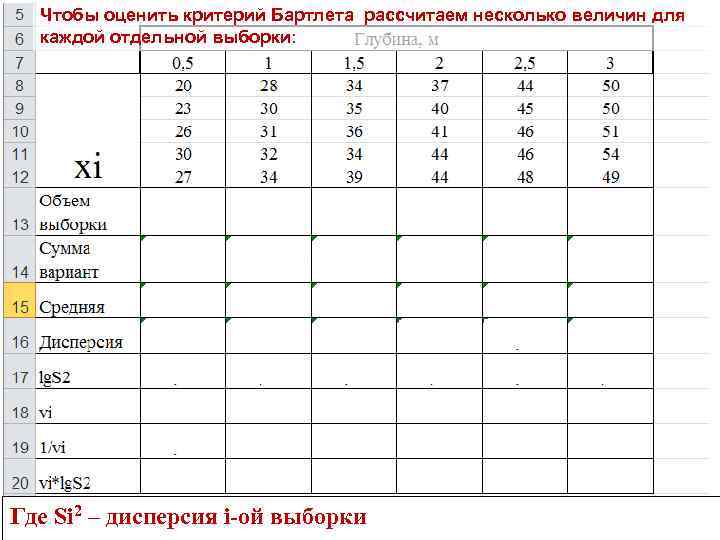 Чтобы оценить критерий Бартлета рассчитаем несколько величин для каждой отдельной выборки: Где Si 2 – дисперсия i-ой выборки
Чтобы оценить критерий Бартлета рассчитаем несколько величин для каждой отдельной выборки: Где Si 2 – дисперсия i-ой выборки
 Чтобы оценить критерий Бартлета рассчитаем несколько величин для каждой отдельной выборки: Где Si 2 – дисперсия i-ой выборки
Чтобы оценить критерий Бартлета рассчитаем несколько величин для каждой отдельной выборки: Где Si 2 – дисперсия i-ой выборки
 Чтобы оценить критерий Бартлета рассчитаем несколько величин для каждой отдельной выборки: Где Si 2 – дисперсия i-ой выборки
Чтобы оценить критерий Бартлета рассчитаем несколько величин для каждой отдельной выборки: Где Si 2 – дисперсия i-ой выборки





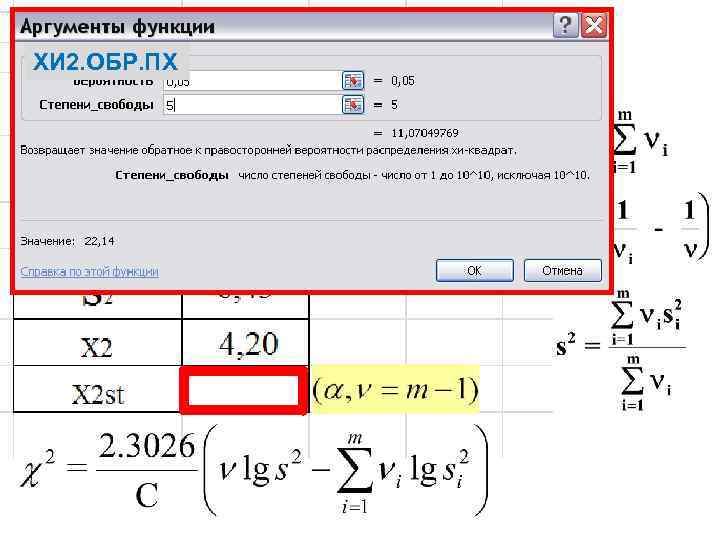 ХИ 2. ОБР. ПХ
ХИ 2. ОБР. ПХ
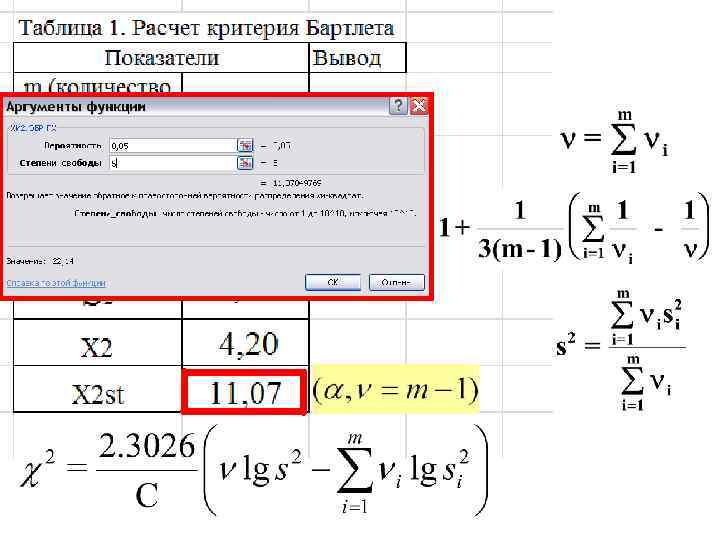
 Следовательно, в пределах исследуемого комплекса отсутствуют значимые различия между дисперсиями отдельных выборок, и вполне правомочно использовать для сравнения выборок аппарат дисперсионного анализа.
Следовательно, в пределах исследуемого комплекса отсутствуют значимые различия между дисперсиями отдельных выборок, и вполне правомочно использовать для сравнения выборок аппарат дисперсионного анализа.
 Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса Но: Наблюдаемые различия между выборочные средними случайны На: Средняя выборочная хотя бы одной выборки отличается от генеральной средней.
Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса Но: Наблюдаемые различия между выборочные средними случайны На: Средняя выборочная хотя бы одной выборки отличается от генеральной средней.
 ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) SS = (Xi-M)2 = X 2 -( X)2/n 2 S = X 2 -( X)2/n n-1 = SS n-1
ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) SS = (Xi-M)2 = X 2 -( X)2/n 2 S = X 2 -( X)2/n n-1 = SS n-1
 ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) SS = (Xi-M)2 = X 2 -( X)2/n 2 S SSa = ni(Xi-M)2 = X 2 -( X)2/n n-1 = SS n-1
ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) SS = (Xi-M)2 = X 2 -( X)2/n 2 S SSa = ni(Xi-M)2 = X 2 -( X)2/n n-1 = SS n-1
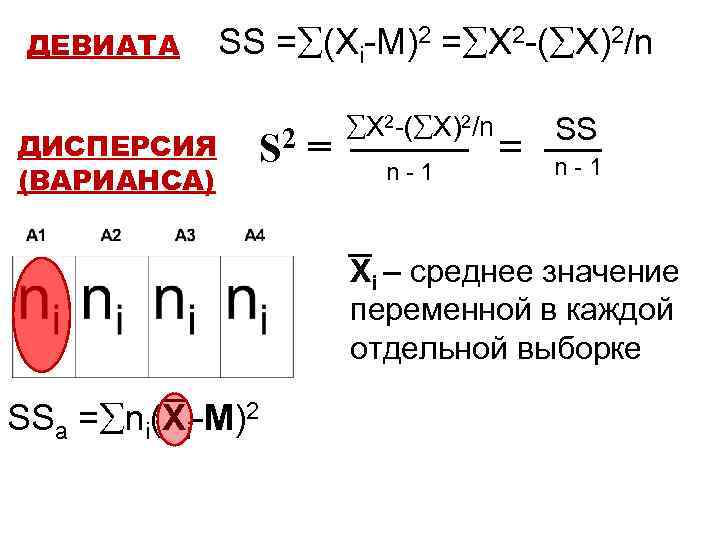 ДЕВИАТА SS = (Xi-M)2 = X 2 -( X)2/n ДИСПЕРСИЯ (ВАРИАНСА) 2 S = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке SSa = ni(Xi-M)2
ДЕВИАТА SS = (Xi-M)2 = X 2 -( X)2/n ДИСПЕРСИЯ (ВАРИАНСА) 2 S = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке SSa = ni(Xi-M)2
 ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
 ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке Xа 1 = (Х 1+Х 2+Х 3)/3= Xi/ni SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке Xа 1 = (Х 1+Х 2+Х 3)/3= Xi/ni SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
 ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке Xа 1 = (Х 1+Х 2+Х 3)/3= Xi/ni SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке Xа 1 = (Х 1+Х 2+Х 3)/3= Xi/ni SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
 ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке Xа 1 = (Х 1+Х 2+Х 3)/3= Xi/ni SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
ДЕВИАТА ДИСПЕРСИЯ (ВАРИАНСА) Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 Х 8 Х 9 SS = (Xi-M)2 = X 2 -( X)2/n 2 S Х 10 Х 11 Х 12 = X 2 -( X)2/n n-1 = SS n-1 Xi – среднее значение переменной в каждой отдельной выборке Xа 1 = (Х 1+Х 2+Х 3)/3= Xi/ni SSa= ni(Xi-M)2=3(Xa 1 -M)2+3(Xa 2 -M)2+3(Xa 3 -M)2+3(Xa 4 -M)2
 Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
 Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
 Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
 Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
Однофакторный дисперсионный анализ – сумма вариант отдельной выборки - Сумма вариант всего комплекса
 Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
 Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
 Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
 Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
Однофакторный дисперсионный анализ Сумма значений вариант всего комплекса Сумма квадратов значений вариант всего комплекса
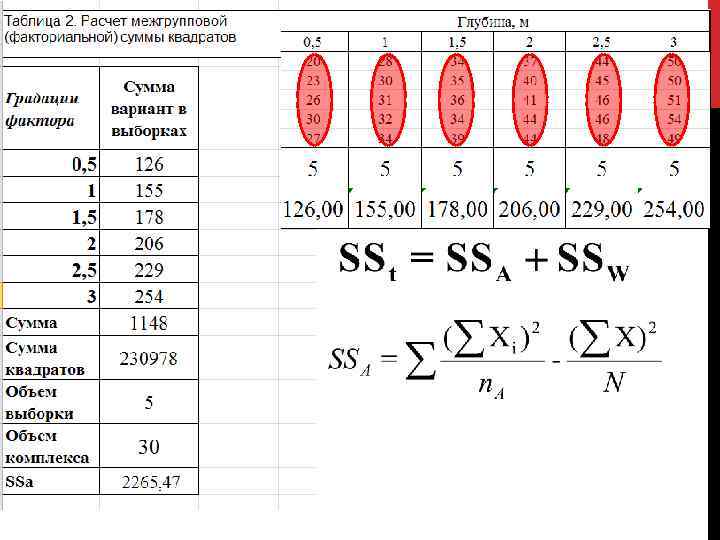
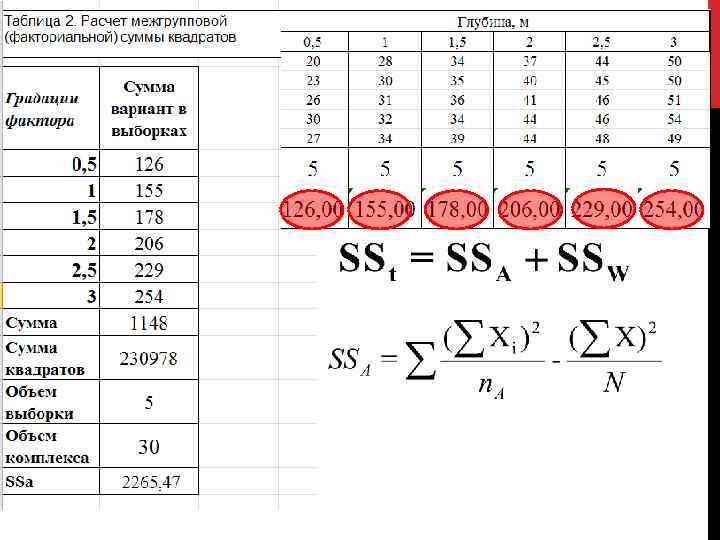
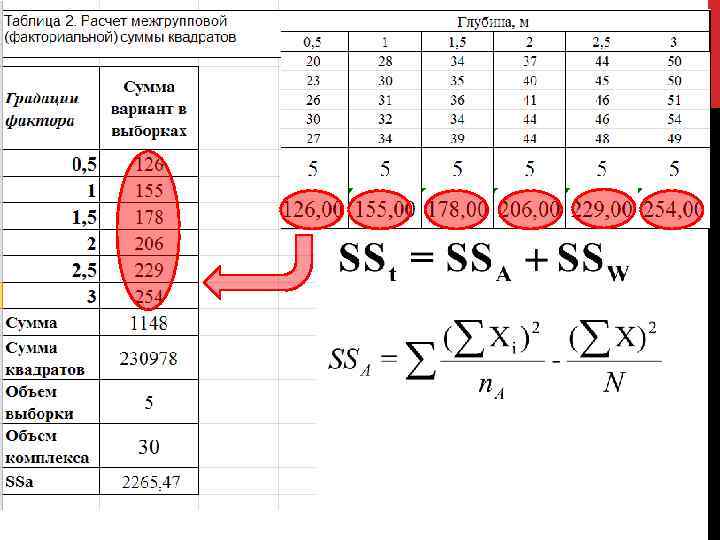
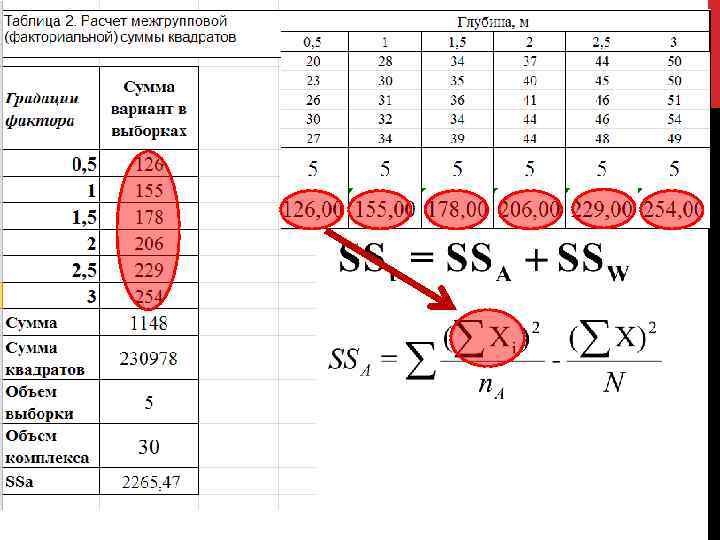
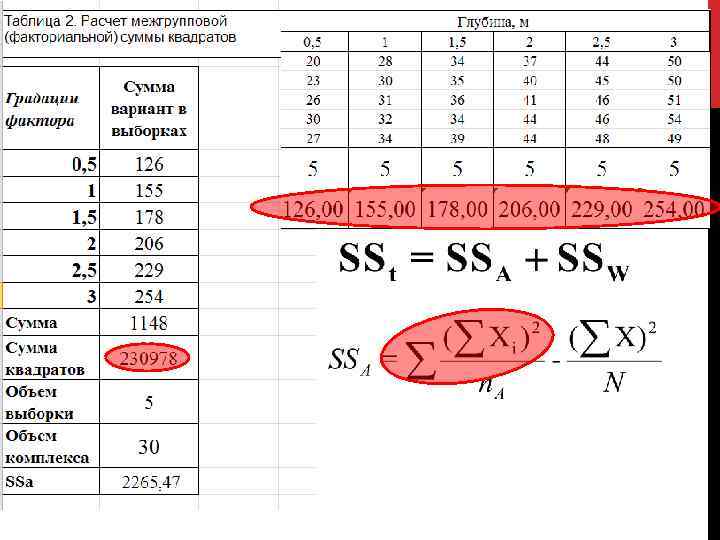
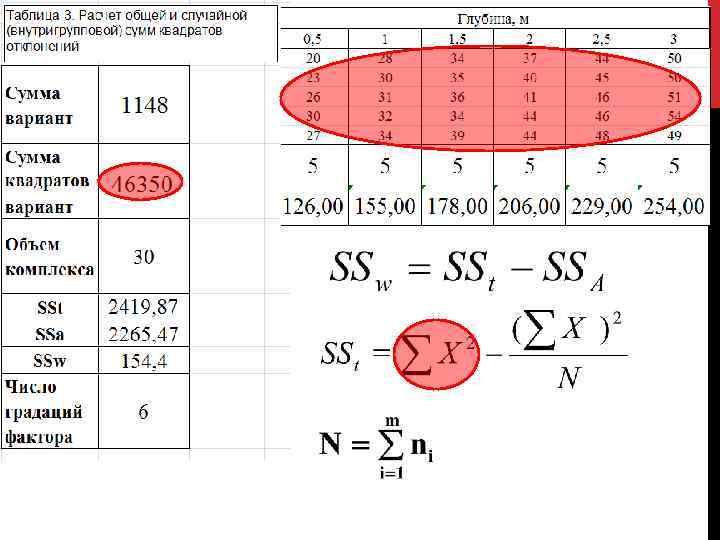
 Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ
 Однофакторный дисперсионный анализ (A) (w) (t)
Однофакторный дисперсионный анализ (A) (w) (t)
 Однофакторный дисперсионный анализ (A) (w) (t)
Однофакторный дисперсионный анализ (A) (w) (t)
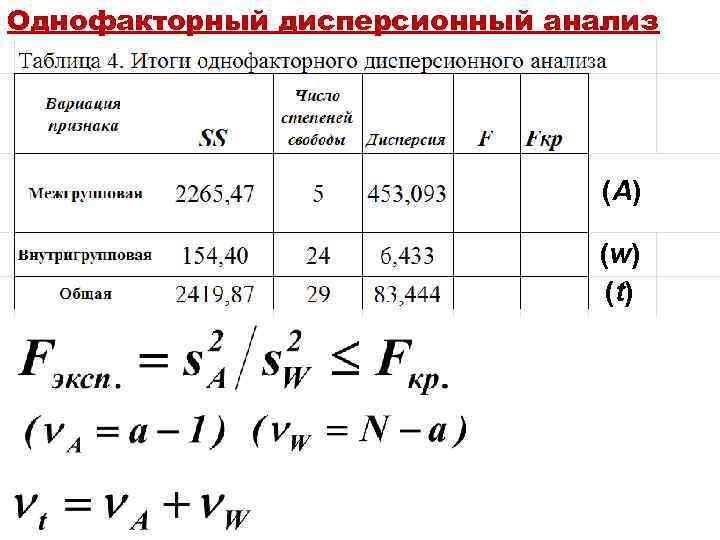 Однофакторный дисперсионный анализ (A) (w) (t)
Однофакторный дисперсионный анализ (A) (w) (t)
 Однофакторный дисперсионный анализ (A) (w) (t)
Однофакторный дисперсионный анализ (A) (w) (t)
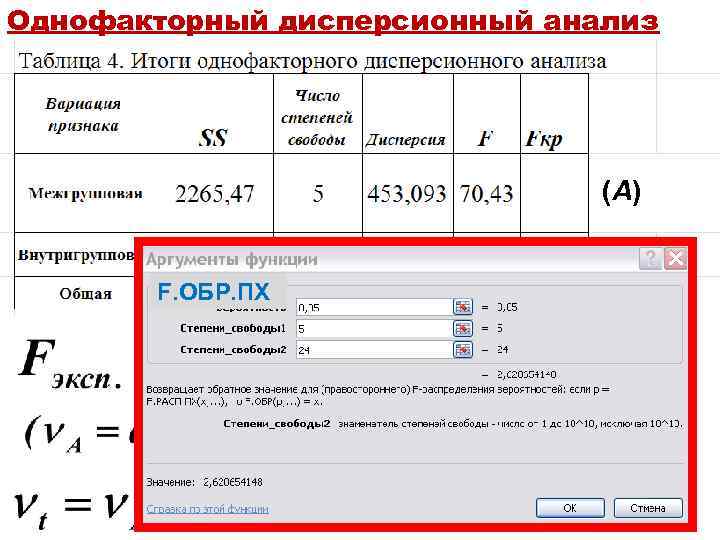 Однофакторный дисперсионный анализ (A) F. ОБР. ПХ (w) (t)
Однофакторный дисперсионный анализ (A) F. ОБР. ПХ (w) (t)
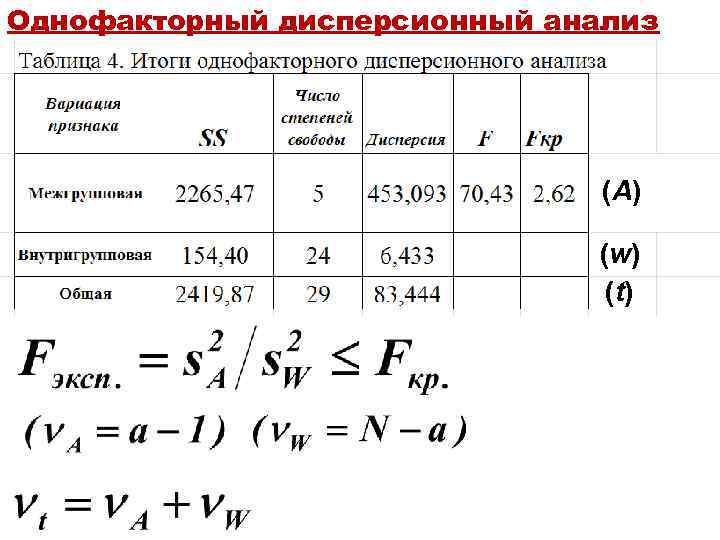 Однофакторный дисперсионный анализ (A) (w) (t)
Однофакторный дисперсионный анализ (A) (w) (t)
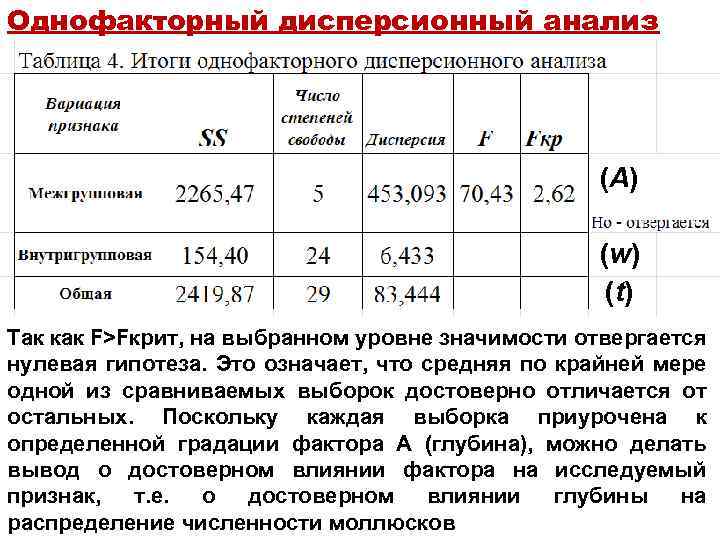 Однофакторный дисперсионный анализ (A) (w) (t) Так как F>Fкрит, на выбранном уровне значимости отвергается нулевая гипотеза. Это означает, что средняя по крайней мере одной из сравниваемых выборок достоверно отличается от остальных. Поскольку каждая выборка приурочена к определенной градации фактора А (глубина), можно делать вывод о достоверном влиянии фактора на исследуемый признак, т. е. о достоверном влиянии глубины на распределение численности моллюсков
Однофакторный дисперсионный анализ (A) (w) (t) Так как F>Fкрит, на выбранном уровне значимости отвергается нулевая гипотеза. Это означает, что средняя по крайней мере одной из сравниваемых выборок достоверно отличается от остальных. Поскольку каждая выборка приурочена к определенной градации фактора А (глубина), можно делать вывод о достоверном влиянии фактора на исследуемый признак, т. е. о достоверном влиянии глубины на распределение численности моллюсков
 СИЛА ВЛИЯНИЯ ФАКТОРА • Определение силы влияния фактора по Снедекору ОЦЕНКА ДОСТОВЕРНОСТИ СИЛЫ ВЛИЯНИЯ ФАКТОРА ПРОВОДИТСЯ ПО КРИТЕРИЮ ФИШЕРА влияние фактора соизмеримо с ошибкой оценки и потому вывод о достоверности силы влияния не надежен. влияние фактора достоверно. ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА:
СИЛА ВЛИЯНИЯ ФАКТОРА • Определение силы влияния фактора по Снедекору ОЦЕНКА ДОСТОВЕРНОСТИ СИЛЫ ВЛИЯНИЯ ФАКТОРА ПРОВОДИТСЯ ПО КРИТЕРИЮ ФИШЕРА влияние фактора соизмеримо с ошибкой оценки и потому вывод о достоверности силы влияния не надежен. влияние фактора достоверно. ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА:
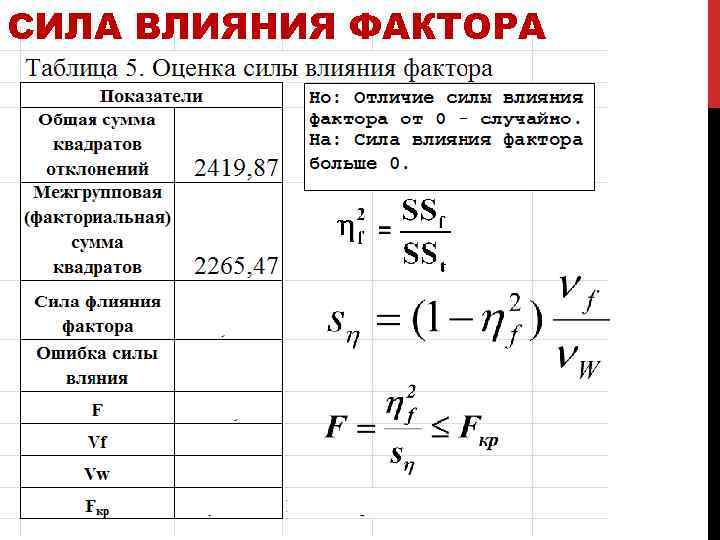
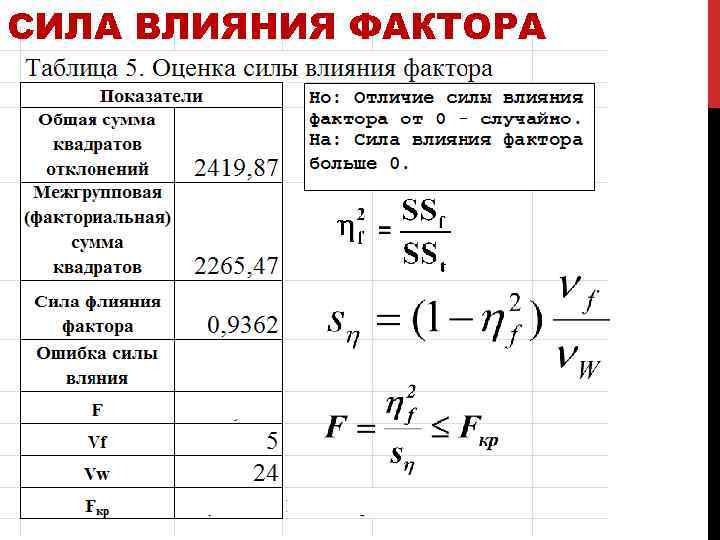
 СИЛА ВЛИЯНИЯ ФАКТОРА • Определение силы влияния фактора по Фишеру ОШИБКА: СТАТИСТИКА: = ОЦЕНКА ДОСТОВЕРНОСТИ СИЛЫ ВЛИЯНИЯ ФАКТОРА ПРОВОДИТСЯ ПО КРИТЕРИЮ ФИШЕРА влияние фактора соизмеримо с ошибкой оценки и потому вывод о достоверности силы влияния не надежен. влияние фактора достоверно. ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА:
СИЛА ВЛИЯНИЯ ФАКТОРА • Определение силы влияния фактора по Фишеру ОШИБКА: СТАТИСТИКА: = ОЦЕНКА ДОСТОВЕРНОСТИ СИЛЫ ВЛИЯНИЯ ФАКТОРА ПРОВОДИТСЯ ПО КРИТЕРИЮ ФИШЕРА влияние фактора соизмеримо с ошибкой оценки и потому вывод о достоверности силы влияния не надежен. влияние фактора достоверно. ПРОВЕРЯЕТСЯ УСЛОВИЕ ОДНОСТОРОННЕГО ТЕСТА:
 СИЛА ВЛИЯНИЯ ФАКТОРА
СИЛА ВЛИЯНИЯ ФАКТОРА
 СИЛА ВЛИЯНИЯ ФАКТОРА
СИЛА ВЛИЯНИЯ ФАКТОРА
 СИЛА ВЛИЯНИЯ ФАКТОРА
СИЛА ВЛИЯНИЯ ФАКТОРА
 СИЛА ВЛИЯНИЯ ФАКТОРА
СИЛА ВЛИЯНИЯ ФАКТОРА
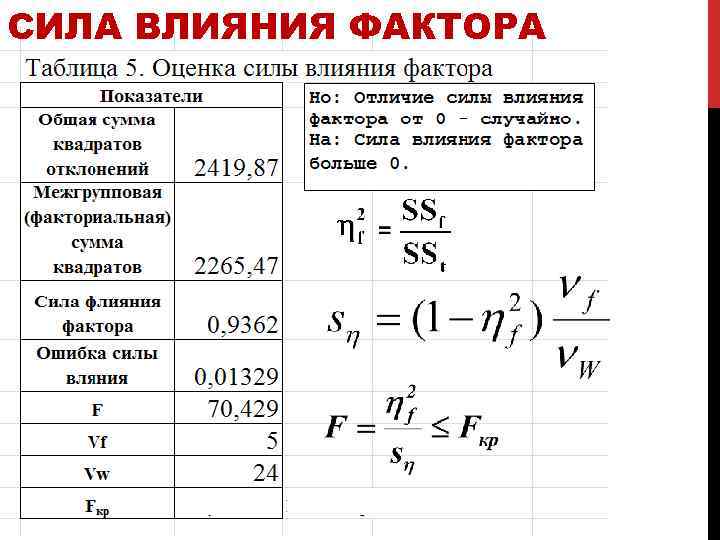 СИЛА ВЛИЯНИЯ ФАКТОРА
СИЛА ВЛИЯНИЯ ФАКТОРА
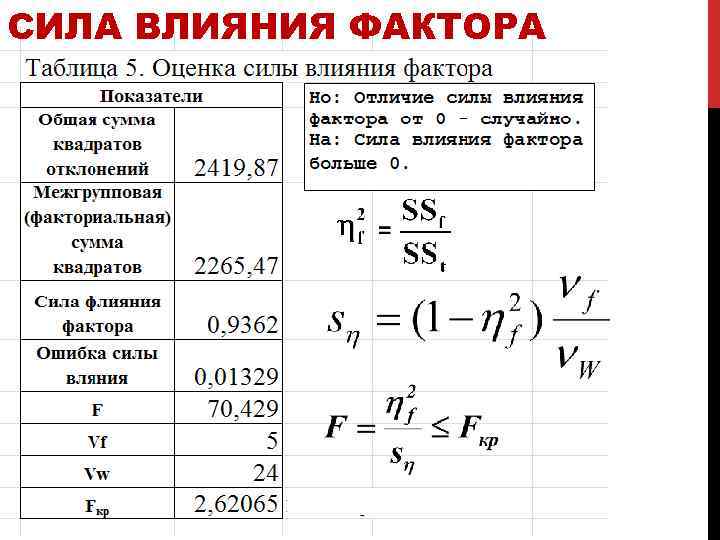 СИЛА ВЛИЯНИЯ ФАКТОРА
СИЛА ВЛИЯНИЯ ФАКТОРА
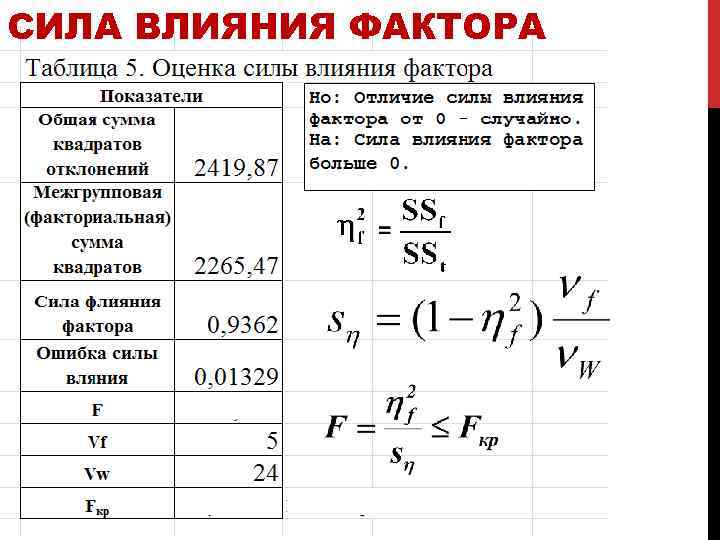
 СИЛА ВЛИЯНИЯ ФАКТОРА В результате мы отвергаем нулевую гипотезу и делаем вывод о достоверности отличия от 0 силы влиянии фактора.
СИЛА ВЛИЯНИЯ ФАКТОРА В результате мы отвергаем нулевую гипотезу и делаем вывод о достоверности отличия от 0 силы влиянии фактора.
 …
…
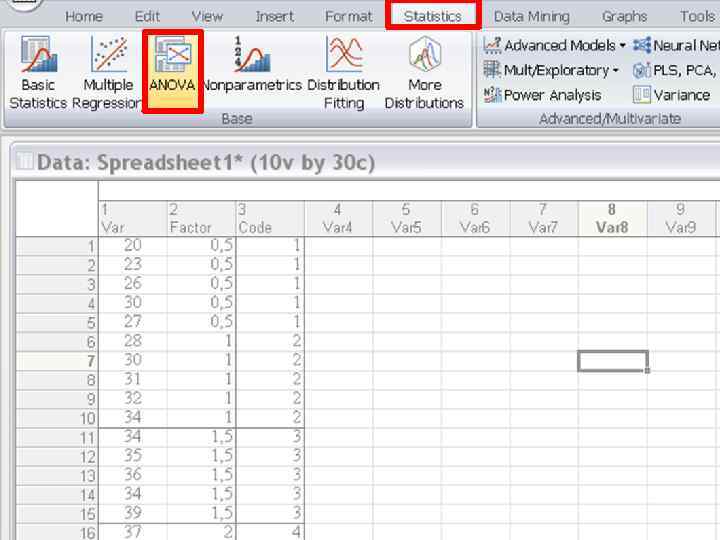

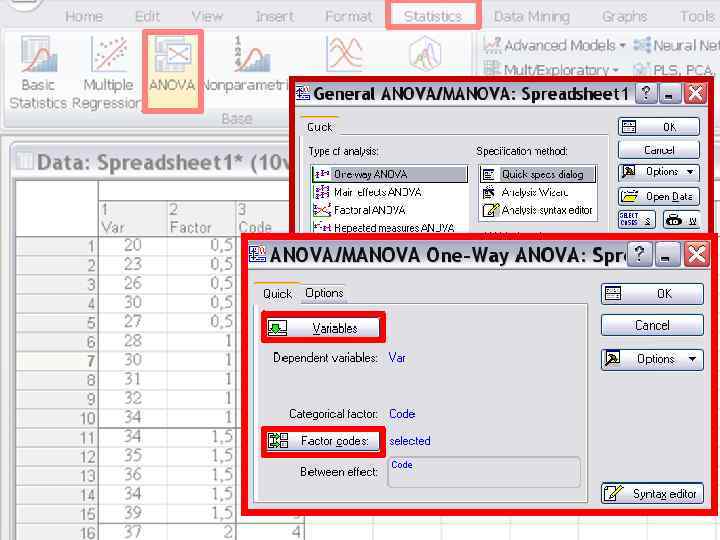
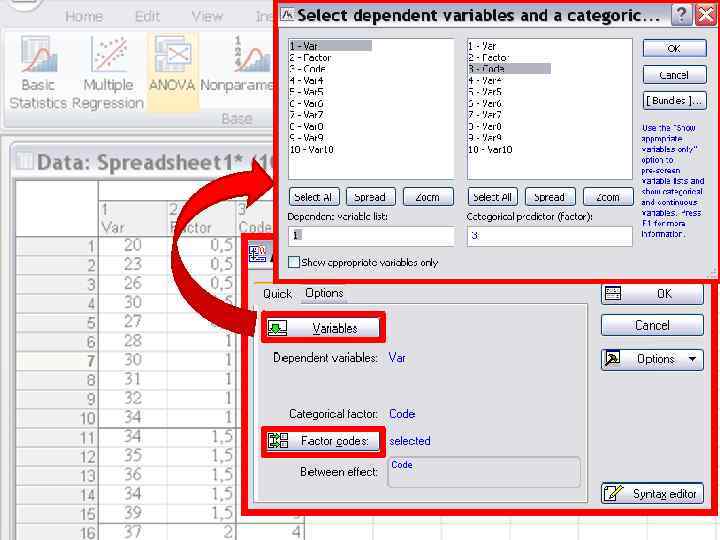
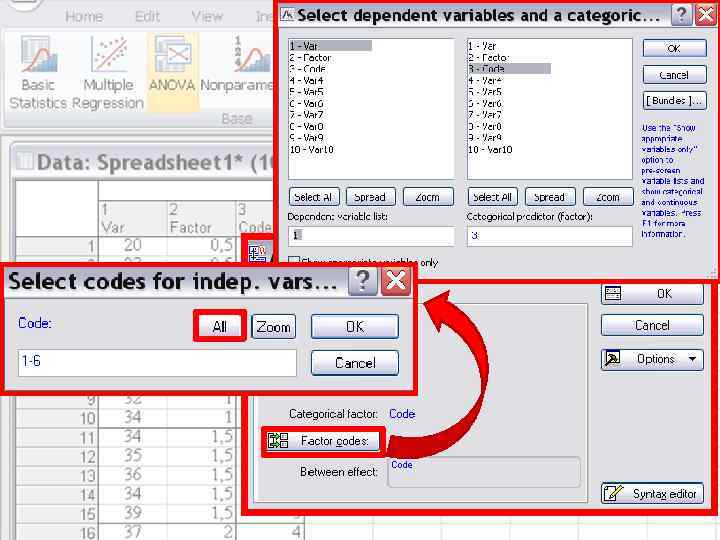
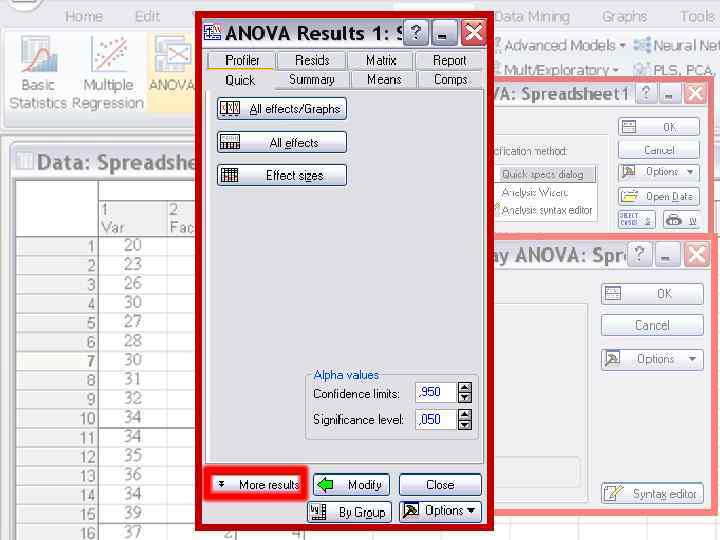
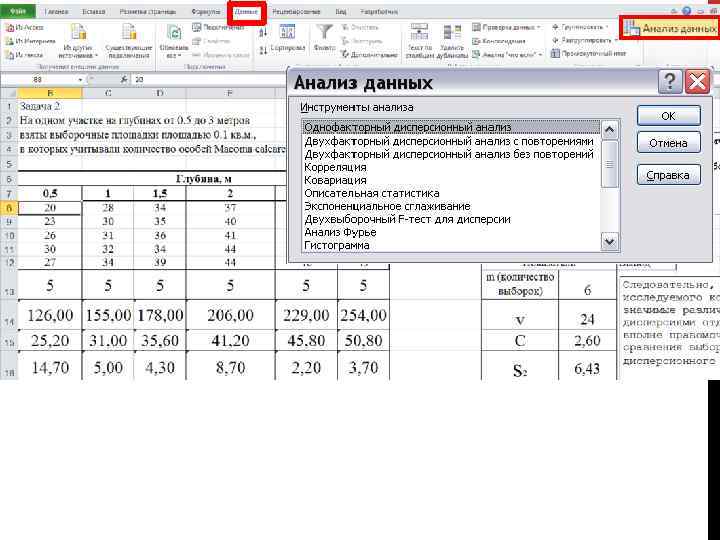
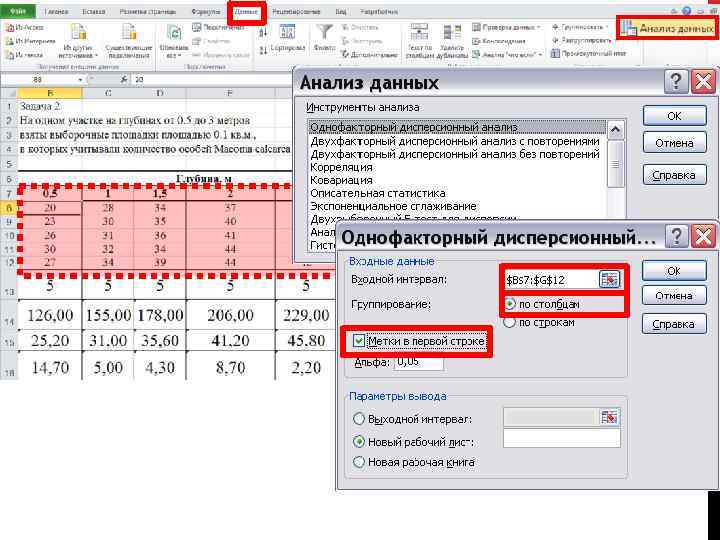
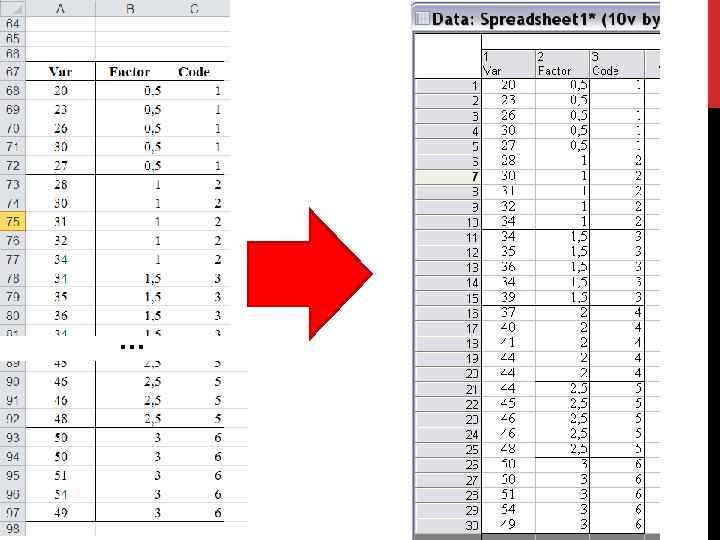
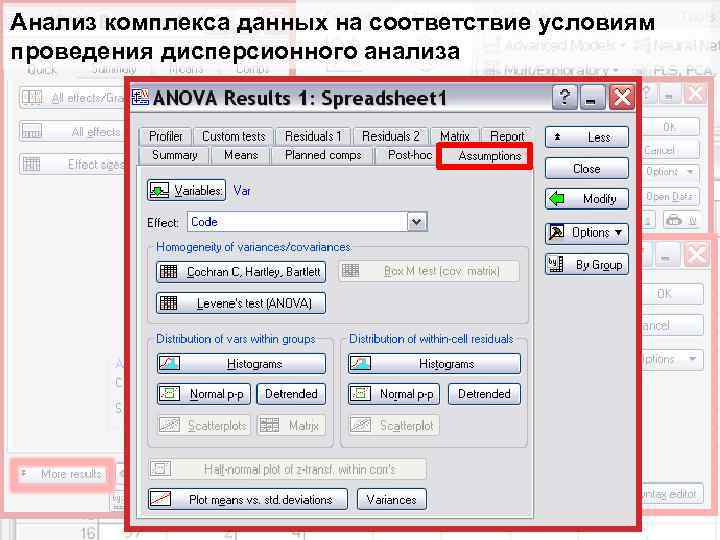 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
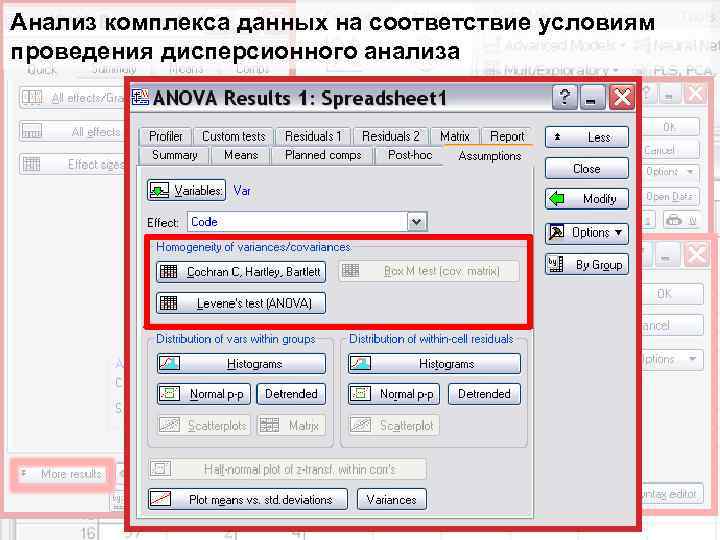 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
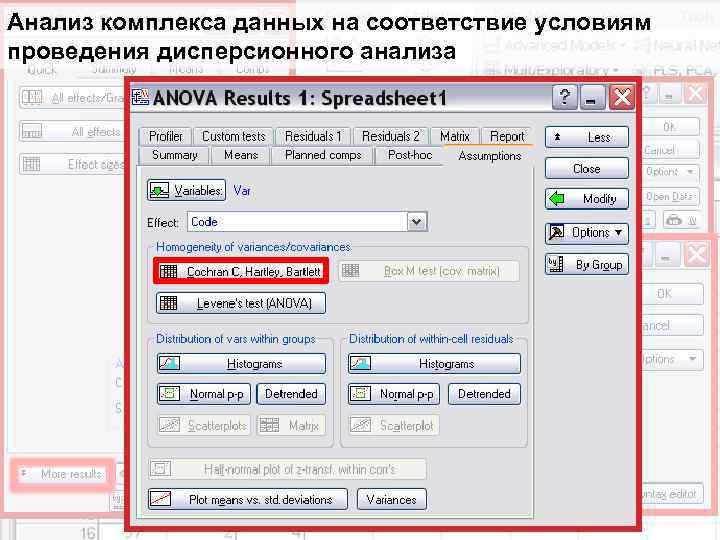 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
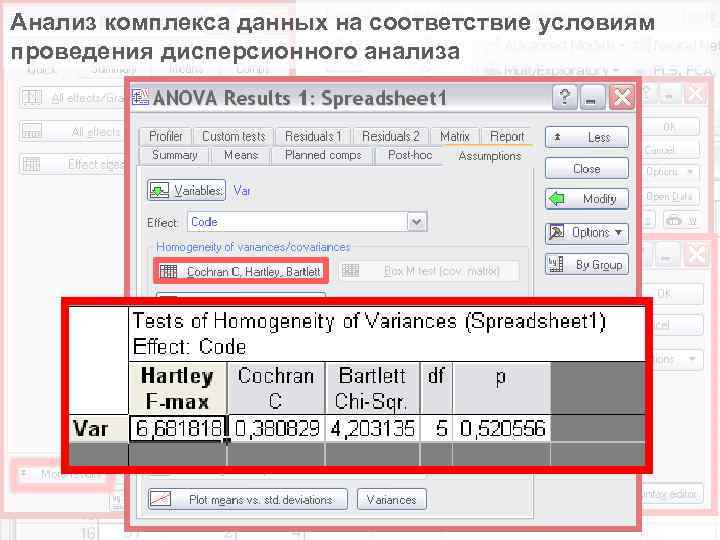 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
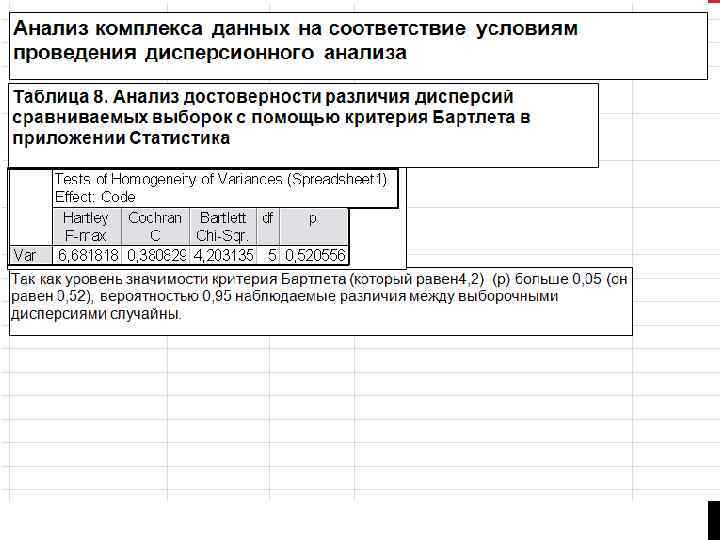
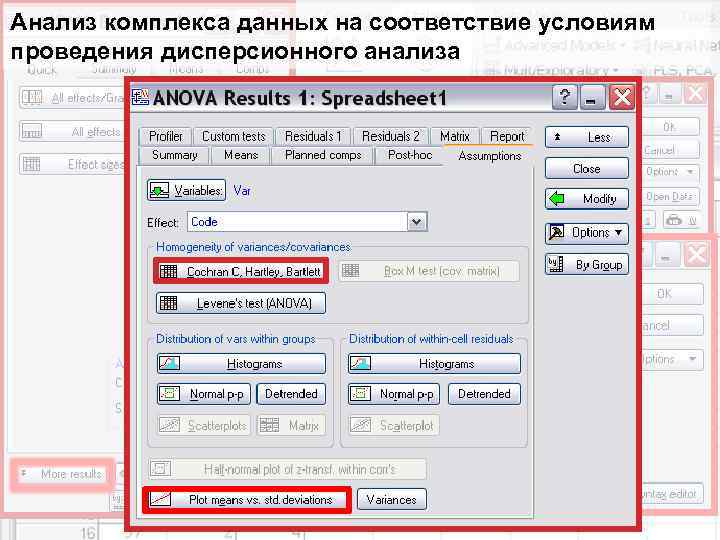 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
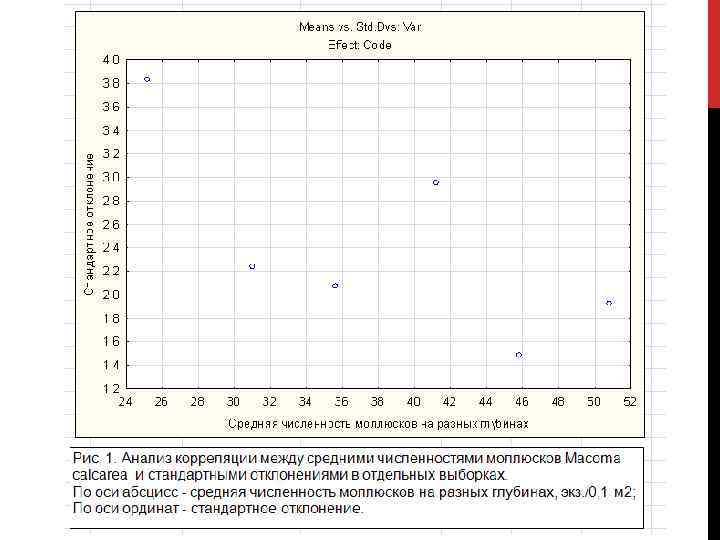
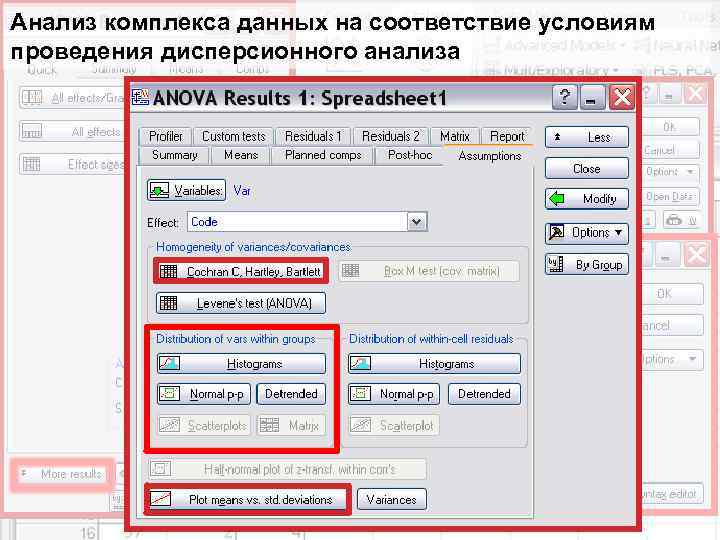 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
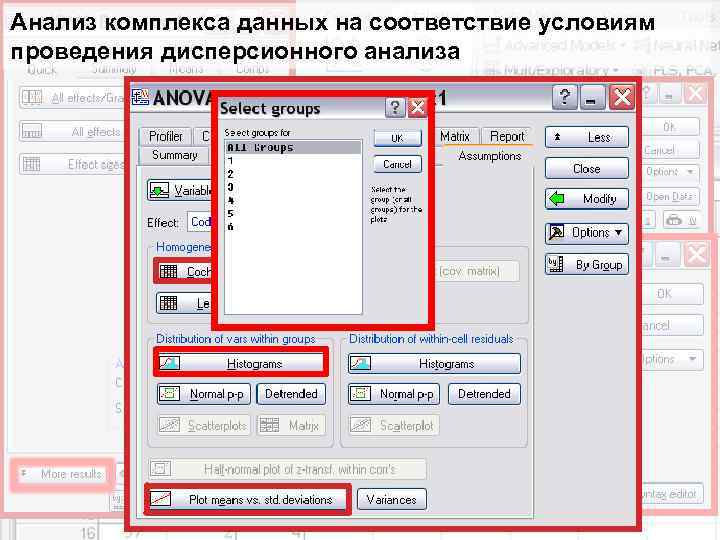 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
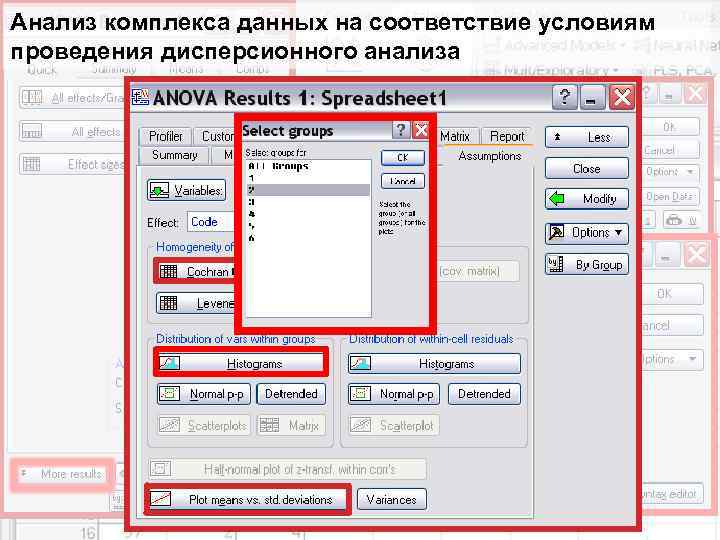 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
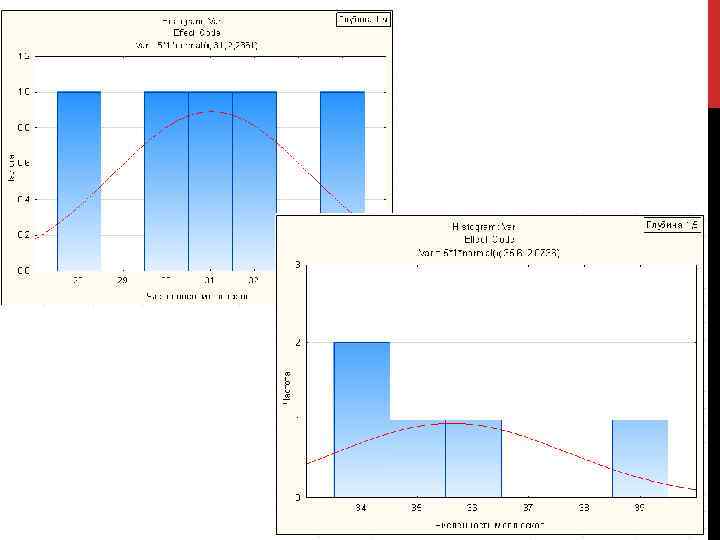
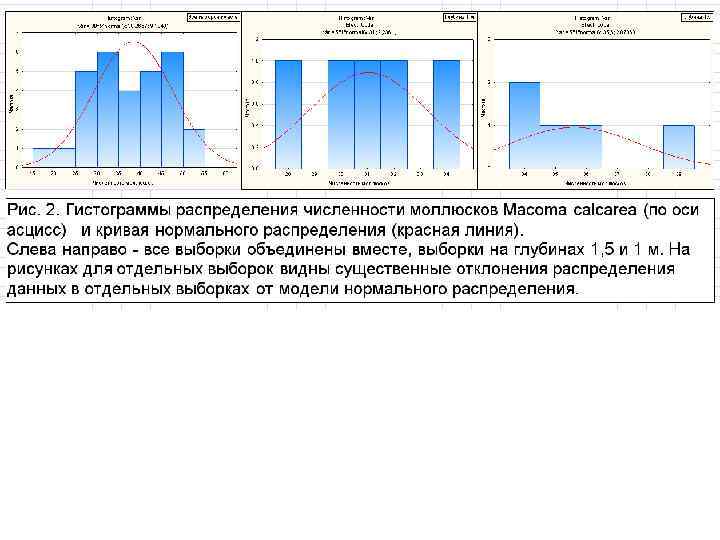
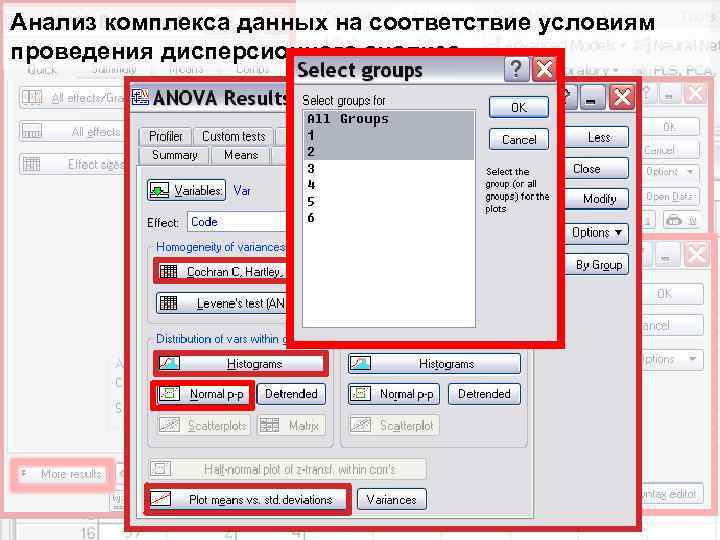 Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
Анализ комплекса данных на соответствие условиям проведения дисперсионного анализа
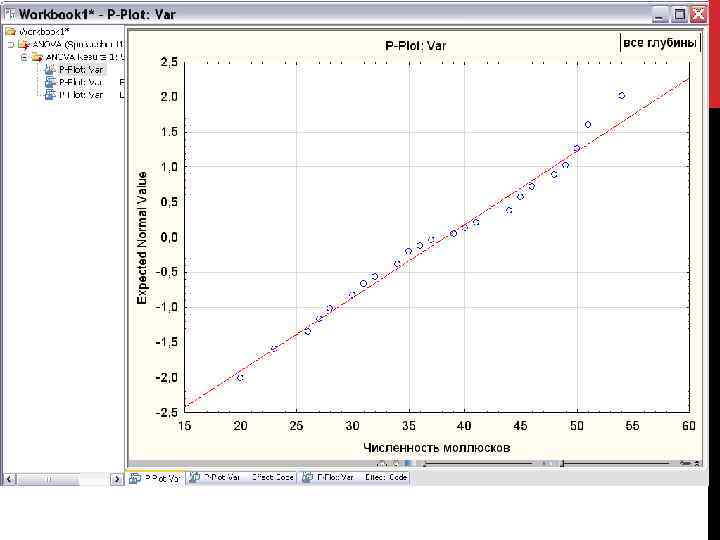
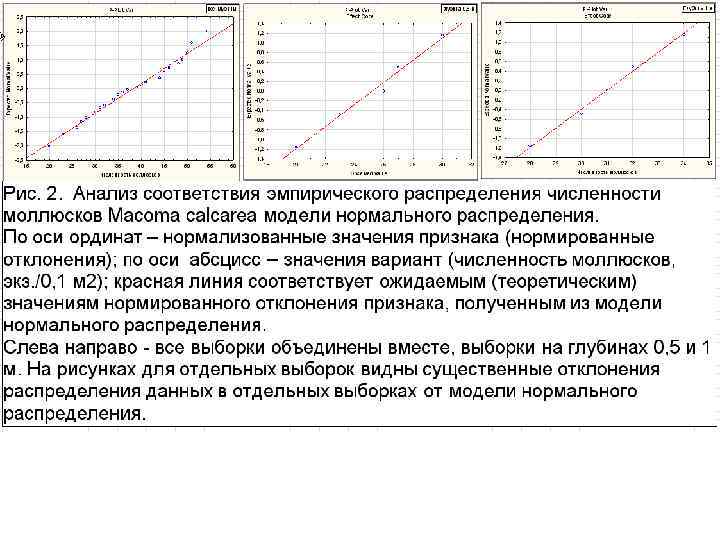
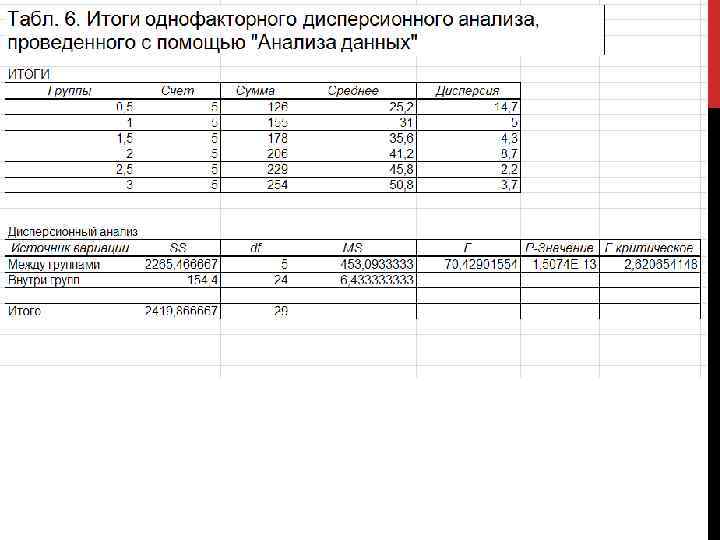
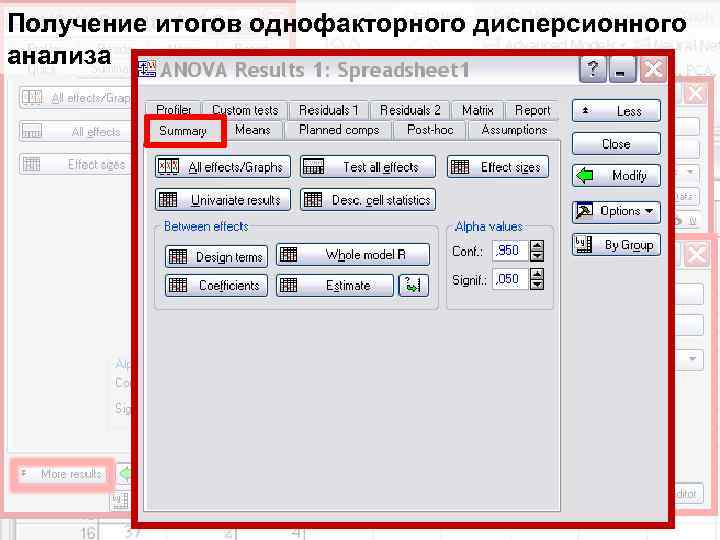 Получение итогов однофакторного дисперсионного анализа
Получение итогов однофакторного дисперсионного анализа
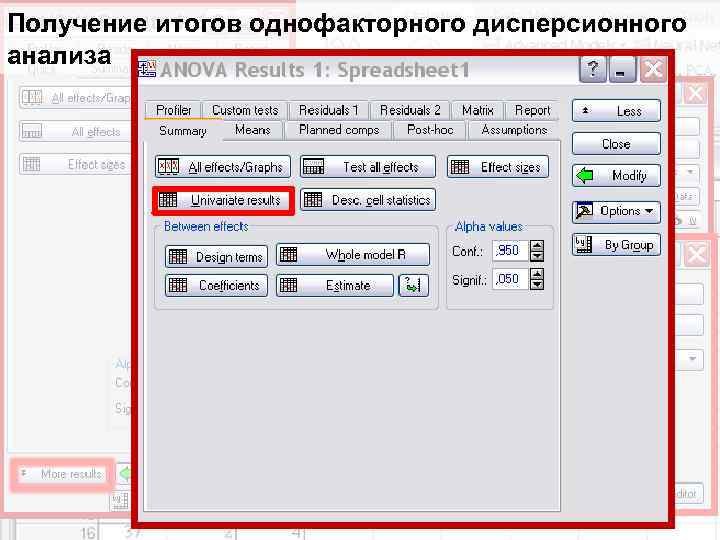 Получение итогов однофакторного дисперсионного анализа
Получение итогов однофакторного дисперсионного анализа
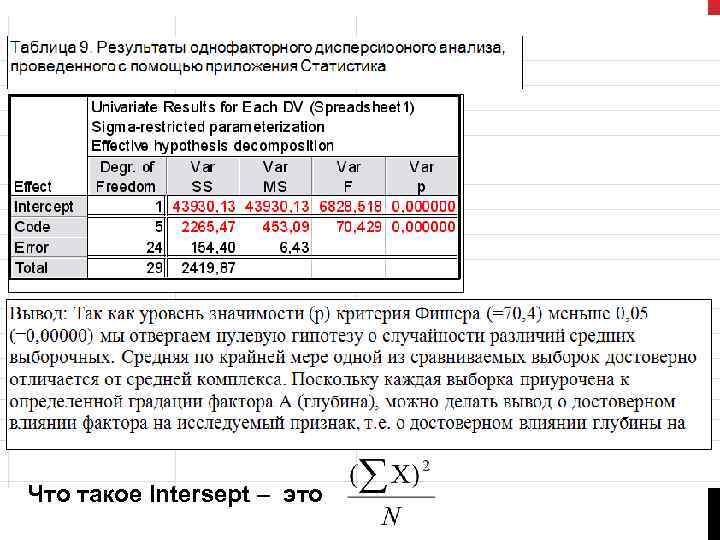 Что такое Intersept – это
Что такое Intersept – это
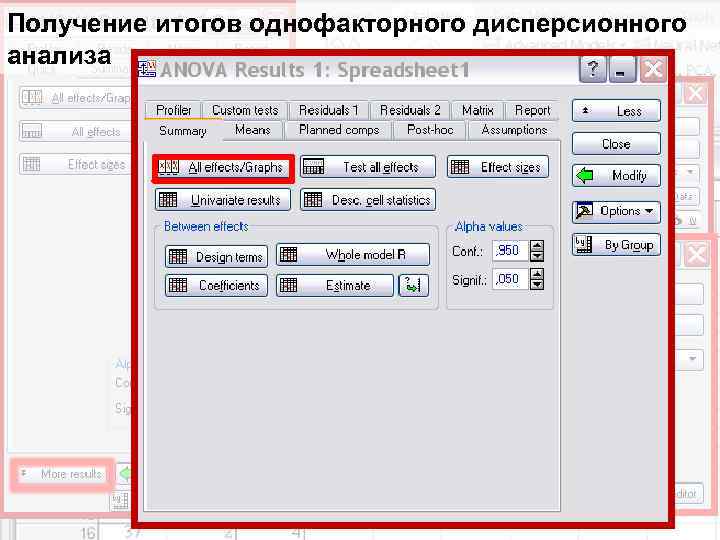 Получение итогов однофакторного дисперсионного анализа
Получение итогов однофакторного дисперсионного анализа
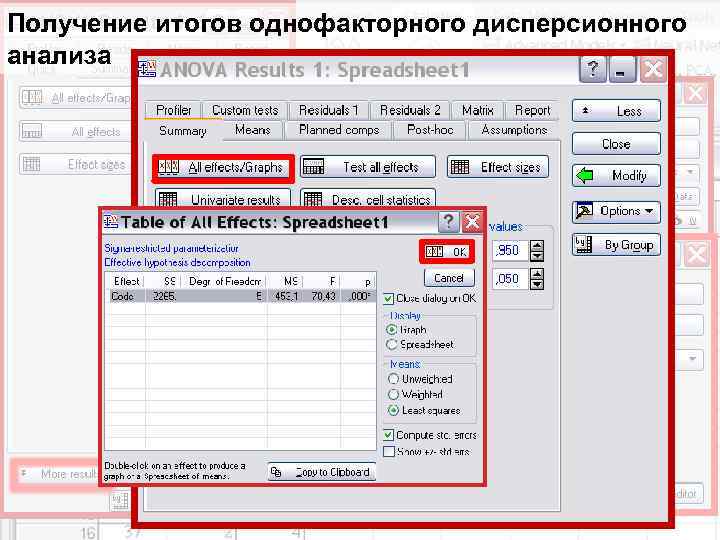 Получение итогов однофакторного дисперсионного анализа
Получение итогов однофакторного дисперсионного анализа