Занятие 6 Уравнение Шредингера 1 Одномерное уравнение Шредингера

Занятие 6. Уравнение Шредингера 1. Одномерное уравнение Шредингера для стационарных состояний 2. Объемная плотность вероятности : Плотность вероятности в одномерном случае : Вероятность обнаружить частицу в интервале от x 1 до x 2 : 3. Энергия частицы, находящейся на n-м энергетическом уровне в прямоугольной одномерной потенциальной яме бесконечной глубины 4. Соответствующая этой энергии собственная волновая функция 5. Вероятность прохождения частицей массой m, имеющей энергию E , прямоугольного потенциального барьера высотой U 0 и шириной l:

1 А. (46. 11) Электрон находится в бесконечно глубоком одномерном потенциальном ящике шириной l. Написать уравнение Шредингера и его решение для области II (0 х l). В области II потенциальная энергия равна нулю (U = 0). Для одномерного потенциального ящика в области (0 < x < l ) состояние электрона описывается одномерным стационарным уравнением Шредингера : (1) Искомое решение уравнения (1) в общем случае обычно записывают в комплексной форме (2). Для практики физический смысл имеет только вещественная форма записи (3) : Найдем частное решение, относящееся к нашей задаче, определив постоянные интегрирования С 1 и С 2. Для этого воспользуемся граничными условиями: (2) (3) (4)

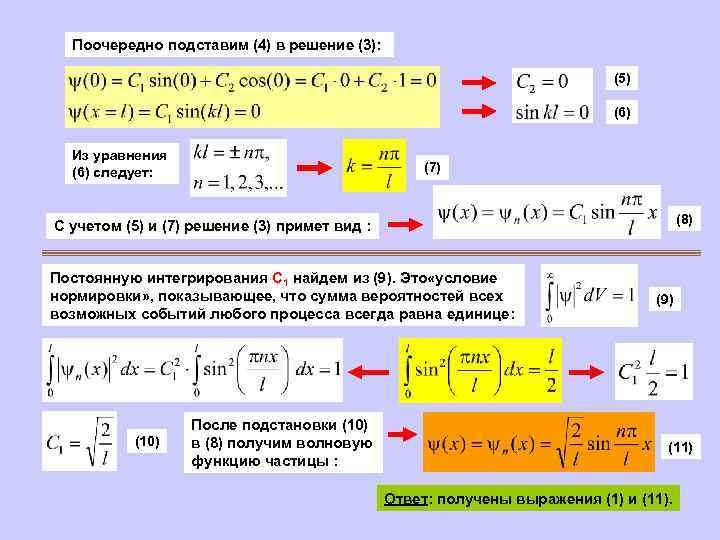Поочередно подставим (4) в решение (3): (5) (6) Из уравнения (6) следует: (7) (8) С учетом (5) и (7) решение (3) примет вид : Постоянную интегрирования С 1 найдем из (9). Это «условие нормировки» , показывающее, что сумма вероятностей всех возможных событий любого процесса всегда равна единице: (10) После подстановки (10) в (8) получим волновую функцию частицы : (9) (11) Ответ: получены выражения (1) и (11).

2 А. (46. 14) Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней Еn+1, n к энергии частицы Еn в трех случаях : 1). n = 3; 2). n = 10; 3). n = . Пояснить полученные результаты. n 1 = 3 n 2 = 10 n 3 = Еn+1, n/ Еn - ? Собственное значение энергии для частицы, находящейся на n-м энергетическом уровне в бесконечно глубоком шириной l потенциальном ящике : (1) Разность соседних уровней энергии Еn+1, n: Относительное расстояние между соседними уровнями энергии: Случай 2: n = 10 (2) Случай 1: n = 3 Случай 3: n = Вывод: при малых номерах энергетических уровней отчетливо виден квантовый характер энергетического спектра. При больших значениях n дискретный характер спектра сглаживается, спектр становится квазинепрерывным.

3 А. (46. 19) Частица в бесконечно глубоком потенциальном ящике шириной l находится в возбужденном состоянии (n = 2). Определить, в каких точках интервала (0 х l ) плотность вероятности нахождения частицы | 2(х)|2 максимальна и минимальна. n = 2 0 х l хmax - ? хmin - ? Собственная волновая функция движущейся частицы, которая находится в потенциальном ящике со стенками бесконечной высоты (см. решение задачи 1 А) : (1) Функция, характеризующая распределение плотности вероятности нахождения частицы внутри ящика в точке с координатой х : (2) Рис. 1. Для n = 2 формула (2) имеет вид: Функция (3) имеет минимум (т. е. нулевое значение) при условии: (3) (4) Уравнение (4) справедливо при условии: (5) Согласно (5) нулевая вероятность нахождения частицы внутри ящика соответствует точкам с координатами х = 0; l/2 и x = l , см. рис. 2.

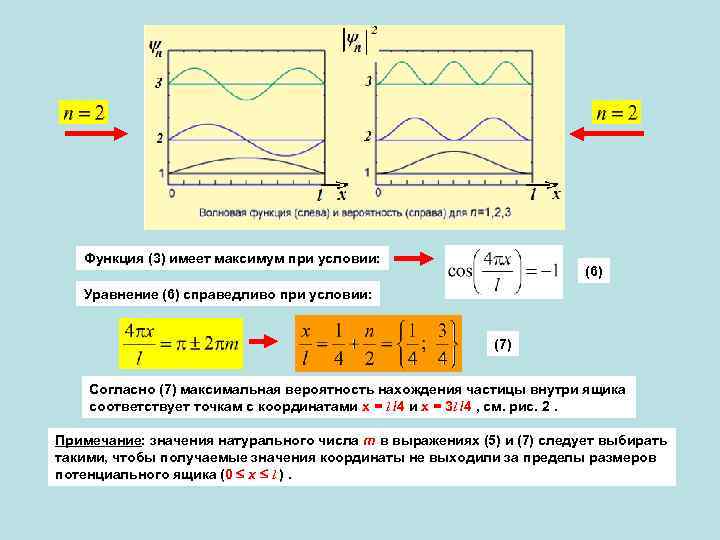Функция (3) имеет максимум при условии: (6) Уравнение (6) справедливо при условии: (7) Согласно (7) максимальная вероятность нахождения частицы внутри ящика соответствует точкам с координатами х = l /4 и x = 3 l /4 , см. рис. 2. Примечание: значения натурального числа m в выражениях (5) и (7) следует выбирать такими, чтобы получаемые значения координаты не выходили за пределы размеров потенциального ящика (0 х l ).

4 А. (46. 20) Электрон находится в потенциальном ящике шириной l. В каких точках интервала ( 0 х l ) плотность вероятности | n(х)|2 нахождения электрона на 1 -м и 2 -м энергетических уровнях одинакова? Вычислить плотности вероятности для этих точек. Решение пояснить графически. Собственная волновая функция движущейся частицы, которая находится в потенциальном ящике со стенками бесконечной высоты (см. решение задачи 1 А) для n = 1 и n = 2 (рис. 1): (1) (2) Функция распределения плотности вероятности нахождения частицы в точке с координатой х внутри ящика: (3) Рис. 1. (5) (4) (6) Учтем равенство плотностей вероятности для n = 1 и n = 2 , используя (5) и (6) : Уравнение (7) выполнимо при равенстве аргументов с точностью до kp : (7) (8)

Проанализируем уравнение (8) с учетом разных знаков ( ) и значений k: 1). k = 1 ( «+» ): (8) (9) Решение (9) не входит в размеры ящика (0 < x/l < 1) 2). k = 1 ( «-» ): (10) 3). k = 2 ( «+» ): При k > 3 решения уравнение (8) при любых знаках ( ) не входят в размеры ящика (0 < x/l < 1). (11) Решение (11) не входит в размеры ящика (0 < x/l < 1) 4). k = 2 ( «-» ): 5). k = 3 ( «+» ): (12) (13) Решение (14) не входит в размеры ящика (0 < x/l < 1) 6). k = 3 ( «-» ): (14) Решение (14) не входит в размеры ящика (0 < x/l < 1) Вывод: плотности вероятностей нахождения электрона на 1 -м и 2 м энергетических уровнях равны между собой в точках с координатами х1 = l /3 и х2 = 2 l /3.

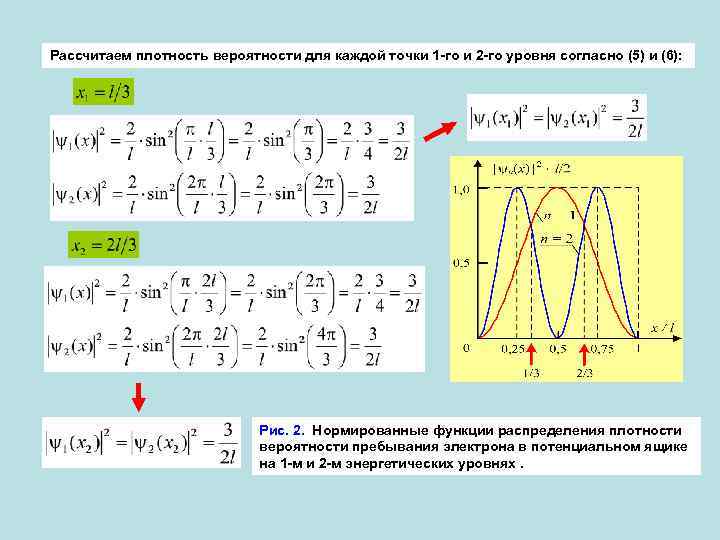Рассчитаем плотность вероятности для каждой точки 1 -го и 2 -го уровня согласно (5) и (6): Рис. 2. Нормированные функции распределения плотности вероятности пребывания электрона в потенциальном ящике на 1 -м и 2 -м энергетических уровнях.

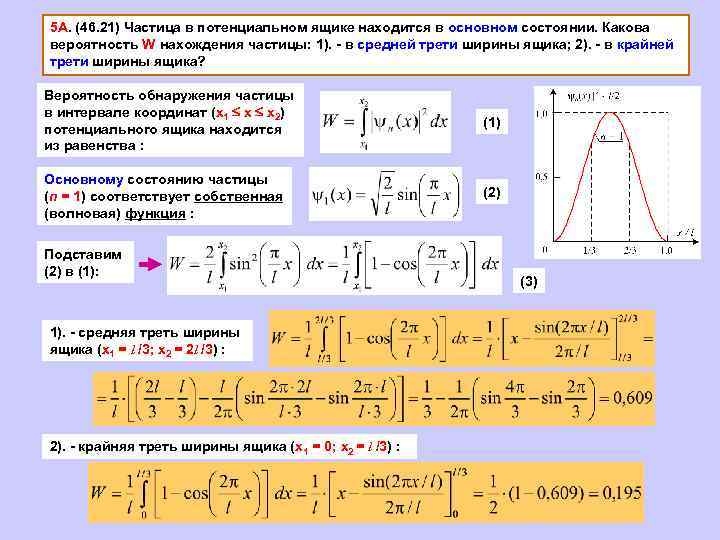5 А. (46. 21) Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W нахождения частицы: 1). - в средней трети ширины ящика; 2). - в крайней трети ширины ящика? Вероятность обнаружения частицы в интервале координат (х1 х х2) потенциального ящика находится из равенства : (1) Основному состоянию частицы (n = 1) соответствует собственная (волновая) функция : (2) Подставим (2) в (1): 1). - средняя треть ширины ящика (х1 = l /3; х2 = 2 l /3) : 2). - крайняя треть ширины ящика (х1 = 0; х2 = l /3) : (3)

6 А. (46. 22) В одномерном потенциальном ящике шириной l находится электрон. Вычислить вероятность W нахождения электрона на 1 -м энергетическом уровне в интервале l /4 , равноудаленном от стенок ящика. Вероятность обнаружения частицы в интервале координат (х1 х х2) потенциального ящика находится из равенства : (1) Первому уровню энергии (n = 1) частицы соответствует собственная (волновая) функция: (2) Подставим (2) в (1): (3) Средней четверти ширины ящика (х1 = 3 l /8; х2 = 5 l /8) соответствует вероятность:

7 А. (46. 24) Вычислить отношение вероятностей W 1/ W 2 нахождения электрона на 1 -м и 2 -м энергетических уровнях в интервале l /4 , равноудаленном от стенок одномерной потенциальной ямы шириной l. Вероятность обнаружения частицы в интервале координат (х1 х х2) потенциального ящика находится из равенства : (1) Первому энергетическому уровню частицы (n = 1) соответствуют собственная (волновая) функция (2) и вероятность (3) : (2) (3) Согласно решению задачи 6 А вероятность пребывания электрона в средней четверти ширины ящика (х1 = 3 l /8; х2 = 5 l /8) равна :

Второму уровню энергии частицы (n = 2) соответствуют собственная (волновая) функция (4) и вероятность (5) : (4) (5) Воспользуемся (5) : вероятность пребывания электрона в средней четверти ширины ящика (х1 = 3 l /8; х2 = 5 l /8) на энергетическом уровне n = 2 равна : Находим отношение вероятностей :