А14. Сложение колебаний и волны.ppt
- Количество слайдов: 12

Занятие № 14 Сложение колебаний и волновые процессы ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ 1. Амплитуда и начальная фаза колебания, полученного при сложении 2 -х колебаний равных частот ( 1 = 2 = ), ориентированных в одном направлении (вдоль оси х ) : 2. Сложение 2 -х взаимно перпендикулярных колебаний с равными частотами ( 1 = 2 = ): 3. Уравнение бегущей плоской упругой волны, распространяющейся вдоль оси x : 4. Уравнение упругой стоячей волны, образующейся при сложении бегущей и отражённой волн, распространяющихся навстречу другу (отражение от менее плотной среды) :

5. Уравнения плоской бегущей электромагнитной волны : 6. Фазовая скорость электромагнитной волны в среде и в вакууме с : 7. Связь напряжённостей электрического и магнитного полей в электромагнитной волне: 8. Объёмная плотность энергии в электромагнитной волне: 9. Показатель преломления среды для электромагнитной волны относительно вакуума: 10. Плотность потока энергии электромагнитной волны (вектор Умова-Пойтинга) : СПРАВОЧНЫЙ МАТЕРИАЛ : Магнитная постоянная 0 = 4 10– 7 Гн/м Электрическая постоянная 0 = 8, 85 10– 12 Ф/м Скорость света в вакууме с = 3 108 м/с
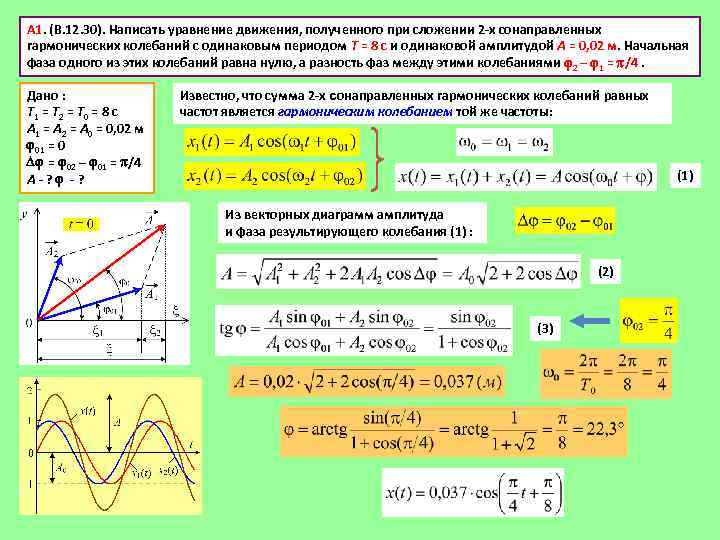
А 1. (В. 12. 30). Написать уравнение движения, полученного при сложении 2 -х сонаправленных гармонических колебаний с одинаковым периодом Т = 8 с и одинаковой амплитудой А = 0, 02 м. Начальная фаза одного из этих колебаний равна нулю, а разность фаз между этими колебаниями 2 – 1 = /4. Дано : Т 1 = Т 2 = Т 0 = 8 с А 1 = А 2 = А 0 = 0, 02 м 01 = 02 – 01 = /4 А-? Известно, что сумма 2 -х сонаправленных гармонических колебаний равных частот является гармоническим колебанием той же частоты: (1) Из векторных диаграмм амплитуда и фаза результирующего колебания (1) : (2) (3)
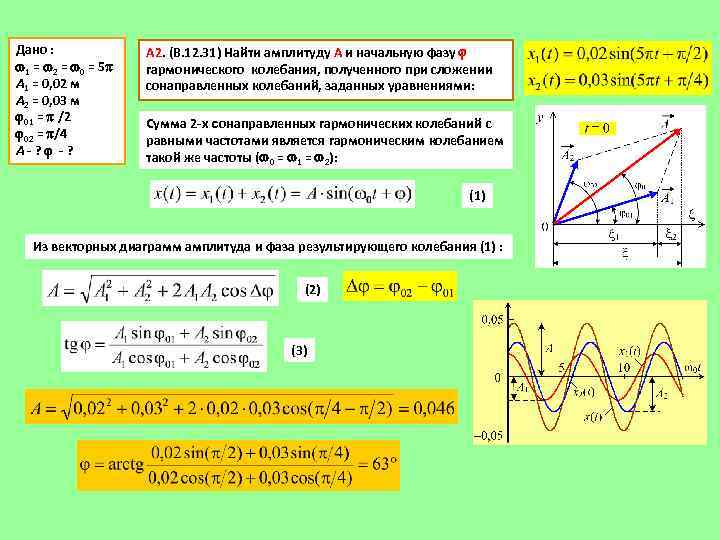
Дано : 1 = 2 = 0 = 5 А 1 = 0, 02 м А 2 = 0, 03 м 01 = /2 02 = /4 А-? А 2. (В. 12. 31) Найти амплитуду А и начальную фазу гармонического колебания, полученного при сложении сонаправленных колебаний, заданных уравнениями: Сумма 2 -х сонаправленных гармонических колебаний с равными частотами является гармоническим колебанием такой же частоты ( 0 = 1 = 2): (1) Из векторных диаграмм амплитуда и фаза результирующего колебания (1) : (2) (3)

А 3. (В. 12. 39). Точка участвует в двух взаимно перпендикулярных колебаниях : Найти траекторию результирующего движения точки. Для нахождения аналитического выражения траектории у(х) результирующего движения точки необходимо в параметрической форме задания этой функции (1) исключить параметр (время t) : Для этого воспользуемся известным соотношением тригонометрии (3) и подставим в него соотношения (2) : (4) Уравнение траектории результирующего движения точки (5) является уравнением окружности (6) с радиусом R : (5) (6) (1) (2) (3)
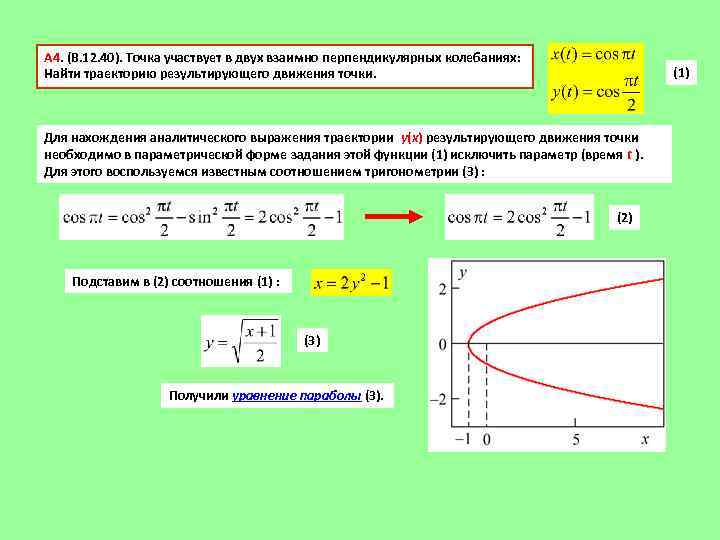
А 4. (В. 12. 40). Точка участвует в двух взаимно перпендикулярных колебаниях: Найти траекторию результирующего движения точки. (1) Для нахождения аналитического выражения траектории у(х) результирующего движения точки необходимо в параметрической форме задания этой функции (1) исключить параметр (время t ). Для этого воспользуемся известным соотношением тригонометрии (3) : (2) Подставим в (2) соотношения (1) : (3) Получили уравнение параболы (3).
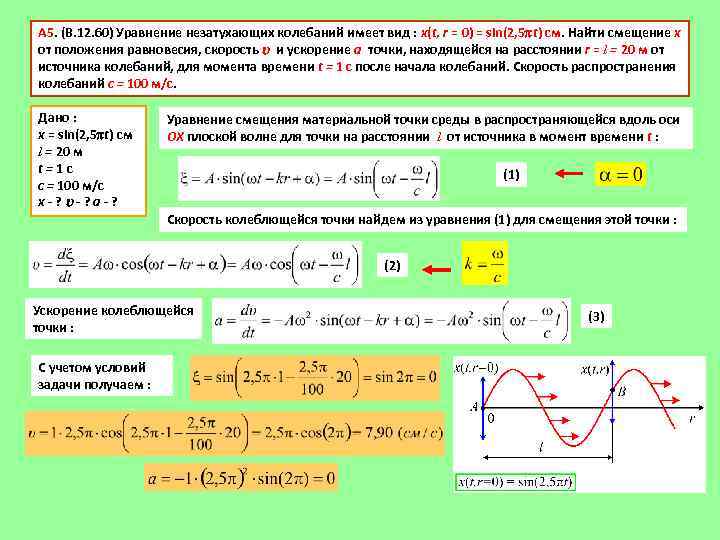
А 5. (В. 12. 60) Уравнение незатухающих колебаний имеет вид : х(t, r = 0) = sin(2, 5 t) см. Найти смещение х от положения равновесия, скорость и ускорение а точки, находящейся на расстоянии r = l = 20 м от источника колебаний, для момента времени t = 1 с после начала колебаний. Скорость распространения колебаний с = 100 м/с. Дано : х = sin(2, 5 t) см l = 20 м t=1 с с = 100 м/с х-? -? а-? Уравнение смещения материальной точки среды в распространяющейся вдоль оси ОХ плоской волне для точки на расстоянии l от источника в момент времени t : (1) Скорость колеблющейся точки найдем из уравнения (1) для смещения этой точки : (2) Ускорение колеблющейся точки : С учетом условий задачи получаем : (3)

А 6. (В. 12. 62) Найти разность фаз колебаний двух точек, лежащих на луче на расстоянии l = 2 м друг от друга, если длина волны = 1 м. Дано : l=2 м =1 м - ? Запишем смещение материальной точки среды для одного и того же момента времени t в точках 1 и 2 соответственно : Разность фаз между колебаниями в точках 1 и 2 среды равны разности полных фаз этих колебаний :

А 7. (В. 12. 65) Найти положение узлов и пучностей, начертить график стоячей волны, если: а) отражение происходит от менее плотной среды; б) отражение происходит от более плотной среды. Длина бегущей волны = 12 см. Стоячая волна - это сумма падающей волны и волны, испытавшей отражение от границы раздела двух сред. При отражении от границы с менее плотной средой фаза волны не меняется (рис. 2). При отражении от более плотной среды фаза волны скачком меняется на (рис. 2). Уравнение падающей и отраженной волн : (1) Уравнение стоячей волны : (2) Используем тригонометрические преобразования и получаем : (3) Первый сомножитель (3) описывает пространственное распределение амплитуды стоячей волны : (4) Положение узлов и пучностей смещения соответствуют координатам, где амплитуда равна нулю или достигает максимума, соответственно : (5) (6)

1). Рассмотрим случай, когда a = 0. Применим условие (5) к выражению (4) и найдем координаты узлов : Применим условие (6) к выражению (4) и найдем координаты пучностей : 2). Рассмотрим случай, когда a = . Применим условие (5) к выражению (4) и найдем координаты узлов : Применим условие (6) к выражению (4) и найдем координаты пучностей :

А 8. (В. 12. 66) Найти длину волны , если расстояние между первой и четвертой пучностями стоячей волны равно l = 15 см. Соседние пучности стоячей волны удалены друг от друга на расстояние половины длины волны : Поэтому расстояние между 1 -й и 4 -й пучностями будет равно : В результате длина волны равна : А 9. (В. 14. 4) Катушка индуктивностью L = 30 мк. Гн присоединена к плоскому конденсатору с площадью пластин S = 0, 01 м 2 и расстоянием между ними d = 0, 1 мм. Найти диэлектрическую проницаемость среды, заполняющей пространство между пластинами, если контур настроен на длину волны = 750 м. Дано : L = 30 мк. Гн S = 0, 01 м 2 d = 0, 1 мм l = 750 м -? Диэлектрическая проницаемость среды и емкость конденсатора связаны соотношением : Длина волны, на которой резонирует контур : ( с – скорость электромагнитных волн в вакууме ) Решим систему уравнений (1) и (2) : (1) Период собственных колебаний в LC-контуре: (2)
А 10. (В. 14. 7) Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид UС = = 50 cos(104 t) В. Емкость конденсатора С = 0, 1 мк. Ф. Найти период колебаний Т, индуктивность L контура, зависимость тока I(t) от времени в цепи и длину волны , соответствующую этому контуру. Дано : UС = 50 cos(104 t), В С = 0, 1 мк. Ф - ? Т - ? L - ? I(t) - ? Длина электромагнитной волны в вакууме, на которую настроен контур (по условию = 104 ): Индуктивность контура найдем, используя выражение для периода колебаний в контуре : Зависимость тока в цепи LC-контура от времени найдем из закона изменения напряжения на конденсаторе :
А14. Сложение колебаний и волны.ppt