Законы распределения случайных величин Основные законы распределения

Законы распределения случайных величин

Основные законы распределения ДИСКРЕТНЫХ случайных величин

Распределение Бернулли Х 0 Р n 1 р q Числовые характеристики:

n Проведем серию опытов, в каждом из которых вероятность появления события А равна р (вероятность непоявления q=1 -р). Испытания заканчиваются, как только появится событие А. Обозначим X - число испытаний, которые нужно провести до первого появления события А. Геометрическое распределение n Случайная величина имеет геометрическое распределение с параметром р, если принимает значения 1, 2, 3… с вероятностями При k=1, 2, . . . , ряд распределения: р, qp, q 2 p, q 3 p, … - геометрический. По этой причине распределение называют геометрическим. n Числовые характеристики:

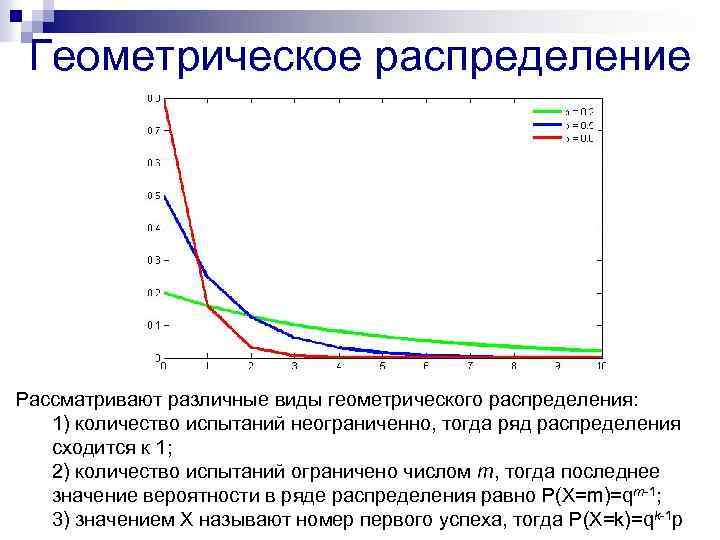Геометрическое распределение Рассматривают различные виды геометрического распределения: 1) количество испытаний неограниченно, тогда ряд распределения сходится к 1; 2) количество испытаний ограничено числом т, тогда последнее значение вероятности в ряде распределения равно P(X=m)=qт-1; 3) значением Х называют номер первого успеха, тогда P(X=k)=qk-1 p

Биномиальное распределение n n n Проведем n опытов. Рассмотрим событие A, которое происходит в каждом опыте с вероятностью p. Число успехов в этой серии опытов - значение случайной величины X. Случайная величина называется распределенной по биномиальному закону с параметрами n и p, если может принимать лишь значения 0, 1, …, n c вероятностями где Числовые характеристики:

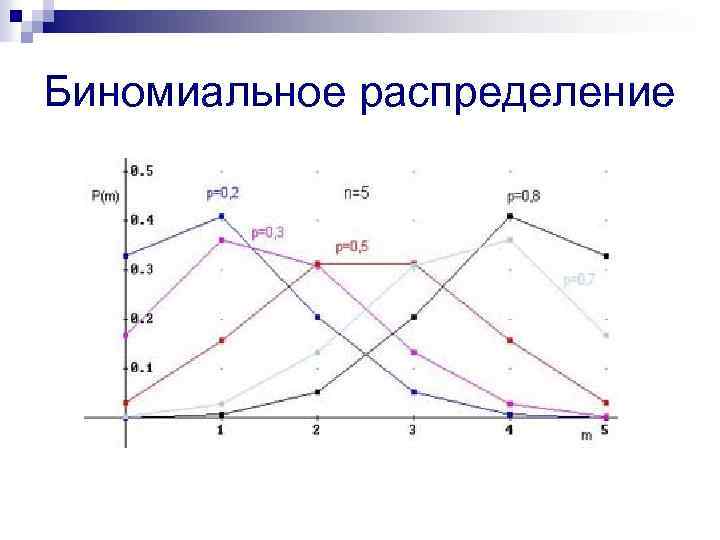Биномиальное распределение

Распределение Пуассона n Случайная величина Х имеет закон распределения Пуассона (закон редких явлений) с параметром λ>0, если она принимает значения 0, 1, 2, …, m, … (бесконечное, но счётное множество значений) с вероятностями n Числовые характеристики:

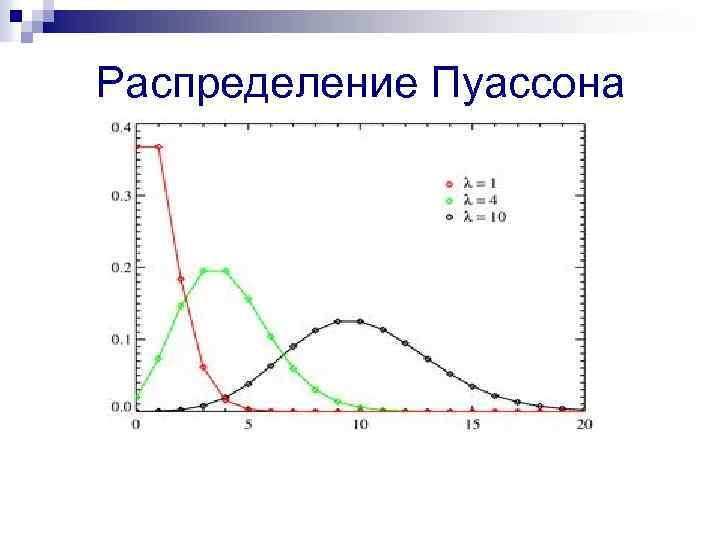Распределение Пуассона

Основные законы распределения НЕПРЕРЫВНЫХ случайных величин

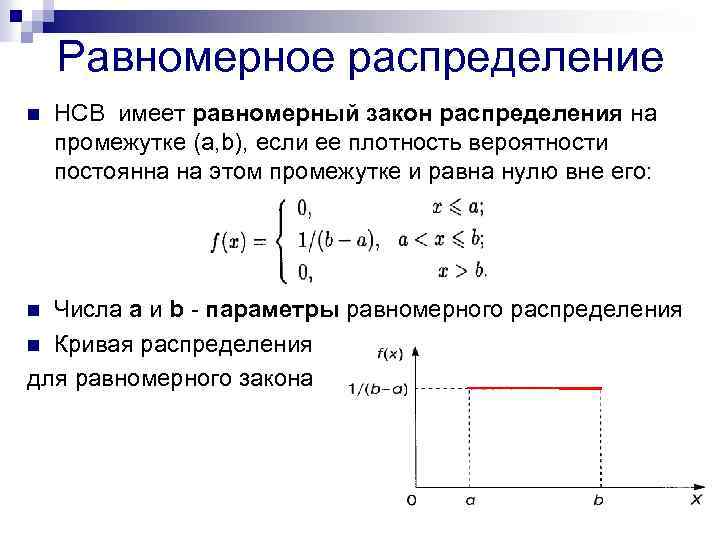Равномерное распределение n НСВ имеет равномерный закон распределения на промежутке (а, b), если ее плотность вероятности постоянна на этом промежутке и равна нулю вне его: Числа а и b - параметры равномерного распределения n Кривая распределения для равномерного закона n

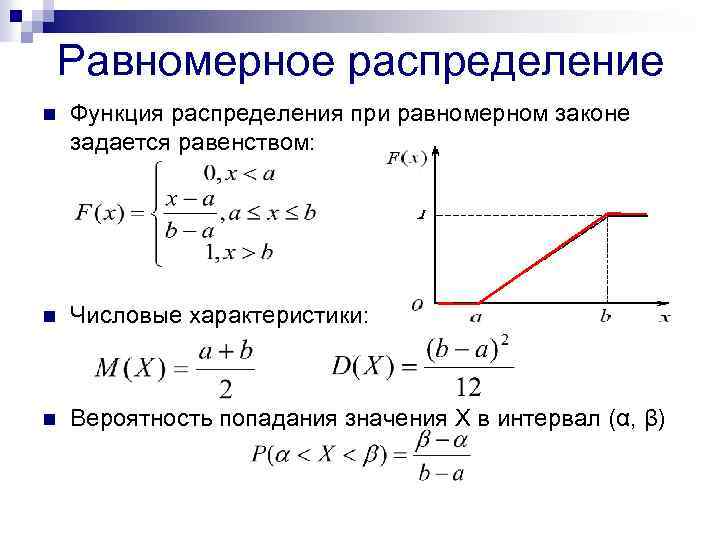Равномерное распределение n Функция распределения при равномерном законе задается равенством: n Числовые характеристики: n Вероятность попадания значения Х в интервал (α, β)

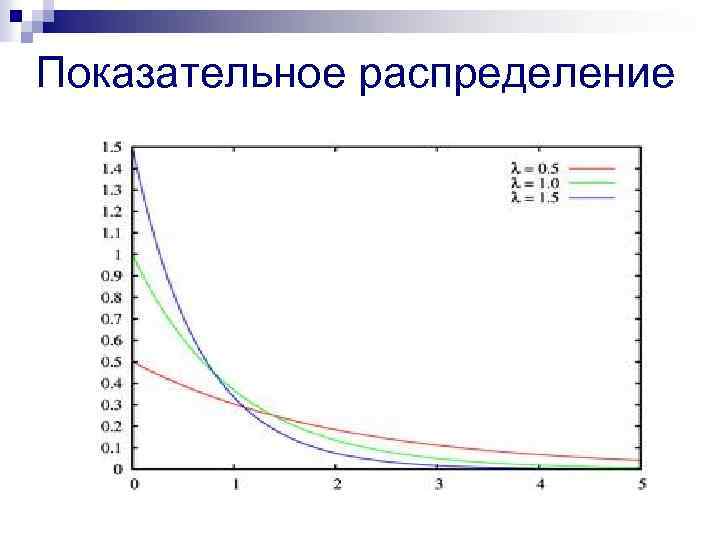
Показательное распределение n НСВ имеет показательный или экспоненциальный закон распределения с параметром μ, если ее плотность вероятности задается выражением: n Показательному распределению подчиняется срок службы различных устройств n Функция распределения имеет вид: n Числовые характеристики: n Вероятность попадания в интервал

Показательное распределение

Нормальное распределение n Непрерывная случайная величина имеет нормальный закон распределения (закон Гаусса) с параметрами а и σ, если ее плотность вероятности имеет вид n Нормальный закон распределения с параметрами а и σ обозначается Основные числовые характеристики при нормальном законе распределения выражаются через его параметры: n

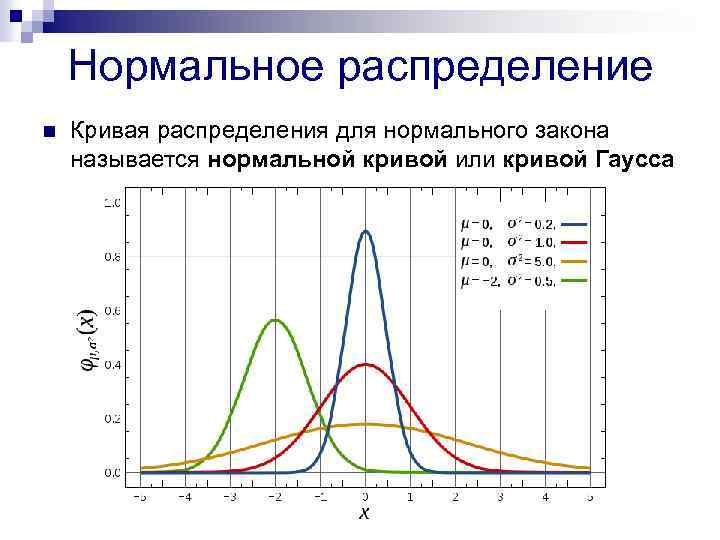Нормальное распределение n Кривая распределения для нормального закона называется нормальной кривой или кривой Гаусса

Нормальное распределение n Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным, стандартным или гауссовым; его плотность равна функции Гаусса: n Функция распределения в случае стандартного нормального распределения совпадает с функцией Лапласа:

Нормальное распределение n Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал равна для гауссова распределения: n Вероятность отклонения случайной величины Х, распределенной по нормальному закону, от ее среднего значения а на величину, не превышающую ε, равна

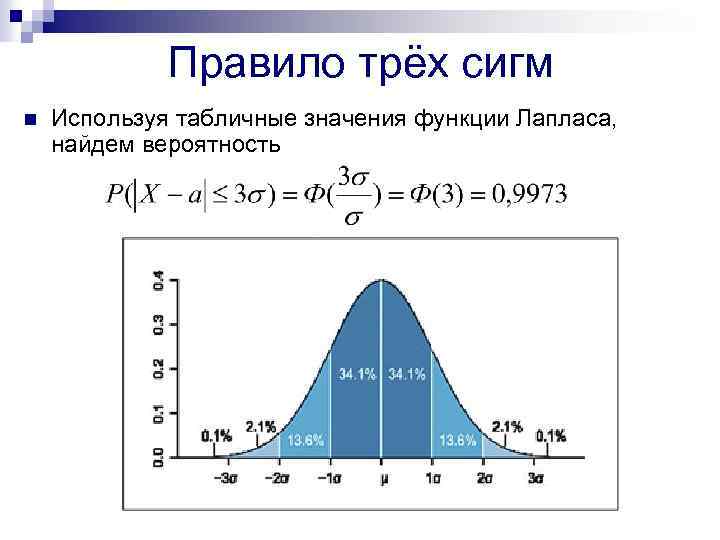Правило трёх сигм n Используя табличные значения функции Лапласа, найдем вероятность

Правило трёх сигм n Эту особенность нормального распределения называют «правилом трёх сигм» . n «Правило трёх сигм» : Если случайная величина имеет нормальный закон распределения с параметрами а и σ, то практически достоверно, что ее значения заключены в интервале