Скачать презентацию Законы распределения непрерывных случайных величин Лекция № Скачать презентацию Законы распределения непрерывных случайных величин Лекция №

Лекция 6_законы.ppt

  • Количество слайдов: 51

Законы распределения непрерывных случайных величин Лекция № 6 Законы распределения непрерывных случайных величин Лекция № 6

Основные законы распределения непрерывных случайных величин Определение Закон распределения случайной величины соотношение, устанавливающее Основные законы распределения непрерывных случайных величин Определение Закон распределения случайной величины соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. В теории ТВ чаще всего используются следующие законы распределения: равномерный закон нормальный (Гаусса), закон Вейбулла, экспоненциальный (показательный) и др.

Распределение Ве йбулла Экспоненциальные распределения — частный случай распределений Вейбулла — Гнеденко. В. Вейбулла Распределение Ве йбулла Экспоненциальные распределения — частный случай распределений Вейбулла — Гнеденко. В. Вейбулла инженер, ввел эти распределения в практику анализа результатов усталостных испытаний, математик Б. В. Гнеденко (1912— 1995), получил такие распределения в качестве предельных при изучении максимального из результатов испытаний.

Доктор Е. Г. Валодди Вейбул (E. H. Waloddi Weibull) 1887 -1979 Доктор Е. Г. Валодди Вейбул (E. H. Waloddi Weibull) 1887 -1979

Распределение Вейбулла двухпараметрическое семейство абсолютно непрерывных распределений Определение. СВ X имеет распределение Вейбулла Распределение Вейбулла двухпараметрическое семейство абсолютно непрерывных распределений Определение. СВ X имеет распределение Вейбулла с параметрами m и a В теории надежности распределение Вейбулла является наиболее общим распределением времени безотказной работы элементов, времени работы до предельного состояния машин.

Надежность Определение Надежность Определение

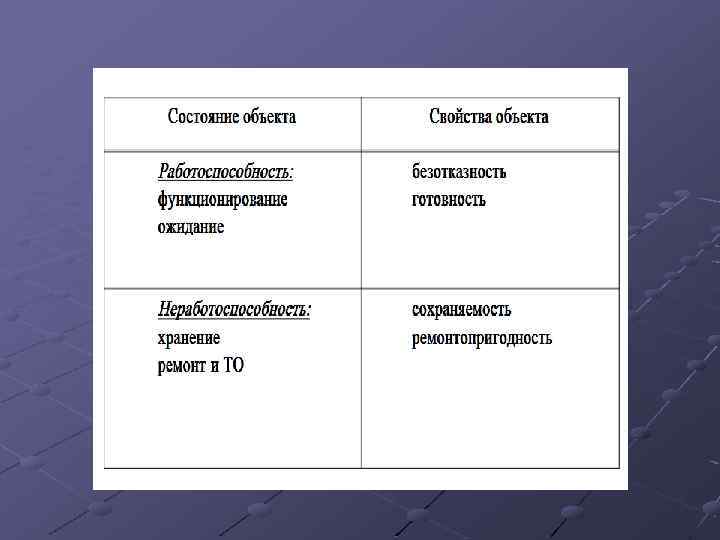
Надежность устройства является . важным показателем качества Определение Функцией риска или функцией интенсивности отказов Надежность устройства является . важным показателем качества Определение Функцией риска или функцией интенсивности отказов и формально определяется h(t) = f(t)/(1 -F(t)) где h(t) обозначает функцию интенсивности отказов или функцию риска в момент t, f(t)- плотность распределения, а F(t) - функцию распределения времен отказов.

Определение Функция надежности (обозначаемая как R(t)) определяется R(t)=1 -F(t)); иногда она называется также функцией Определение Функция надежности (обозначаемая как R(t)) определяется R(t)=1 -F(t)); иногда она называется также функцией выживания (т. к. описывает вероятность того, что отказ произойдет после определенного момента времени t

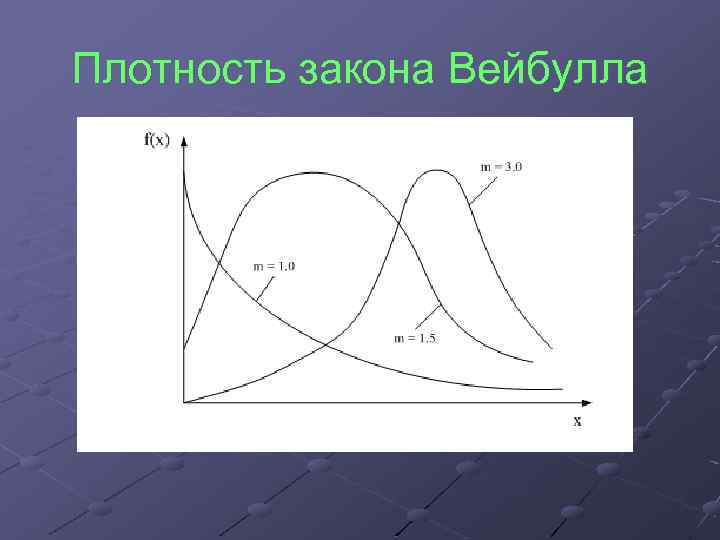Плотность закона Вейбулла Плотность закона Вейбулла

Замечание Значение параметра m зависит от коэффициента вариации и определяется по таблицам, расчетом Замечание Значение параметра m зависит от коэффициента вариации и определяется по таблицам, расчетом или графоаналитическим путем. Величина его влияет на форму дифференциальной кривой. Замечание При m = 1 распределение Вейбулла преобразуется в экспоненциальное Замечание при m = 2, 5. . . 3, 5 и V = 0, 3. . . 0, 4 — приближается к нормальному.

Функция распределения Функция плотности распределения Функция распределения Функция плотности распределения

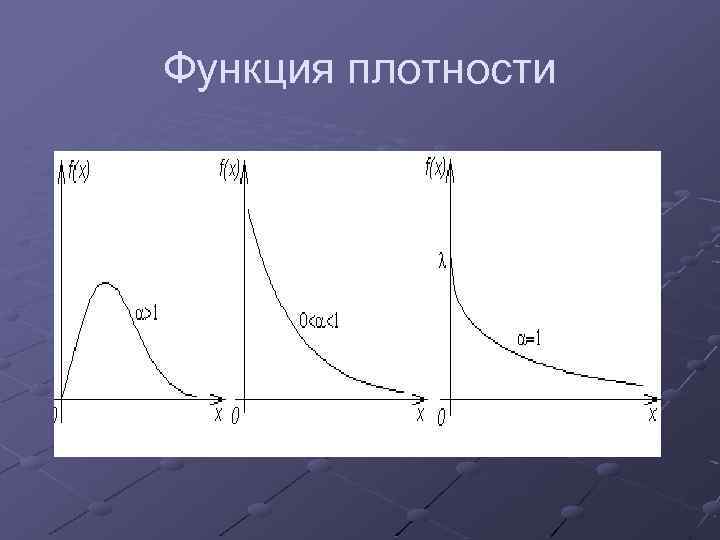Функция плотности Функция плотности

Замечание. Если α = 1, то распределение Вейбулла превращается в показательное распределение. Замечание. СВ, Замечание. Если α = 1, то распределение Вейбулла превращается в показательное распределение. Замечание. СВ, имеющая распределение Вейбулла, встречается в задачах надежности при оценке времени безотказной работы прибора

Нормальное распределение Определение. Нормальное распределение вероятностей непрерывной случайной величины распределение, которое описывается плотностью Нормальное распределение Определение. Нормальное распределение вероятностей непрерывной случайной величины распределение, которое описывается плотностью вероятности термин был впервые использован Гальтоном в 1889 г. , также иногда называемое законом Гаусса, определяется следующим образом , где a – математическое ожидание, медиана и мода распределения,

Замечание одномерное нормальное распределение является двухпараметрическим семейством распределений нормальное распределение определяется двумя параметрами: Замечание одномерное нормальное распределение является двухпараметрическим семейством распределений нормальное распределение определяется двумя параметрами: а и σ. Замечание Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному

Пример Показания счётчика Гейгера, регистрирующего количество пролетевших сквозь него за 1 секунду элементарных частиц, Пример Показания счётчика Гейгера, регистрирующего количество пролетевших сквозь него за 1 секунду элементарных частиц, подчиняются распределению Найдите математическое ожидание показаний счётчика Предположим, что распределение нормальное a = 1000, σ = 50. Тогда частиц в секунду. 1000.

Частным случаем нормального распределения является логарифмически нормальное. Оно легко получается из нормального заменой x Частным случаем нормального распределения является логарифмически нормальное. Оно легко получается из нормального заменой x на ln x: Здесь учтено, что

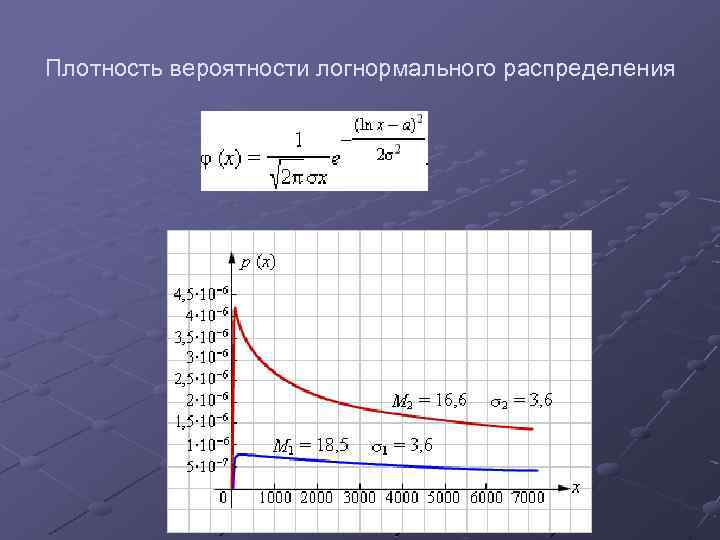Плотность вероятности логнормального распределения Плотность вероятности логнормального распределения

История открытия Часто нормальное распределение называют распределением Гаусса, или Муавра, в честь тех, История открытия Часто нормальное распределение называют распределением Гаусса, или Муавра, в честь тех, кто, как считается, открыл его — Карл Фридрих Гаусс (1777 1855) и, веком ранее, что не так достоверно, Авраам де Муавр (1667 1754).

Доска Галтона вертикально установленная доска в форме равнобедренного треугольника. В доске расположены колышки, Доска Галтона вертикально установленная доска в форме равнобедренного треугольника. В доске расположены колышки, один в верхнем ряду, два во втором, и так далее. Каждый последующий ряд имеет на один колышек больше. Колышки в сечении треугольные, так что, когда падает шарик, у него есть вероятность 50/50 пойти вправо или влево. В основании доски находится серия желобов для подсчета попаданий каждого броска.

Шарики, падающие через доску Галтона и достигающие желобов, начинают формировать нормальное распределение. Чем «глубже» Шарики, падающие через доску Галтона и достигающие желобов, начинают формировать нормальное распределение. Чем «глубже» доска (то есть чем больше рядов она имеет) и чем больше шариков бросается, тем больше конечный результат будет напоминать нормальное распределение

Фрэнсис Гальтон Сэр Фрэнсис Гальтон (англ. Francis Galton; 16 февраля 1822 — 17 Фрэнсис Гальтон Сэр Фрэнсис Гальтон (англ. Francis Galton; 16 февраля 1822 — 17 января 1911) — английский исследователь, вклад во многих областях науки: метеорология (антициклон и первые общедоступные погодные карты), статистику (регресс и корреляция), психологию (синестезия), биологию (природа и механизмы наследственности) и криминологию (отпечатки пальцев). математически обосновал практическую невозможность совпадения отпечатков пальцев у людей

Нормальное распределение дает хорошую модель для реальных явлений, в которых: 1) имеется сильная тенденция Нормальное распределение дает хорошую модель для реальных явлений, в которых: 1) имеется сильная тенденция данных группироваться вокруг центра; 2) положительные и отрицательные отклонения от центра равновероятны; 3) частота отклонений быстро падает, когда отклонения от центра становятся большими

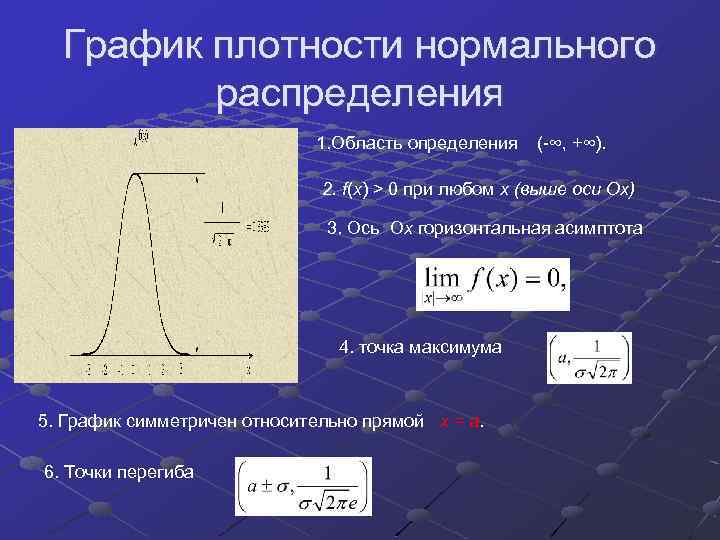График плотности нормального распределения 1. Область определения ( ∞, +∞). 2. f(x) > График плотности нормального распределения 1. Область определения ( ∞, +∞). 2. f(x) > 0 при любом х (выше оси Ox) 3. Ось Ох горизонтальная асимптота 4. точка максимума 5. График симметричен относительно прямой х = а. 6. Точки перегиба

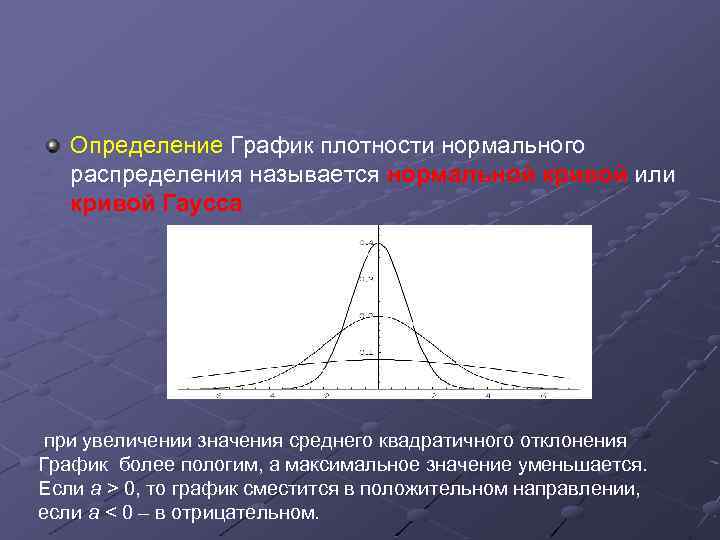Определение График плотности нормального распределения называется нормальной кривой или кривой Гаусса при увеличении Определение График плотности нормального распределения называется нормальной кривой или кривой Гаусса при увеличении значения среднего квадратичного отклонения График более пологим, а максимальное значение уменьшается. Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

Функция распределения q. Интеграл «неберущийся» , который невозможно выразить через элементарные функции. q. Функция распределения q. Интеграл «неберущийся» , который невозможно выразить через элементарные функции. q. Поэтому для вычисления значений F(x) используют таблицы. q Таблицы составлены для случая, когда а = 0, а σ = 1. Определение Нормальное распределение с параметрами а = 0, σ = 1 называется нормированным, а его функция распределения – функция Лапласа Интеграл функция Лапласа вероятностей

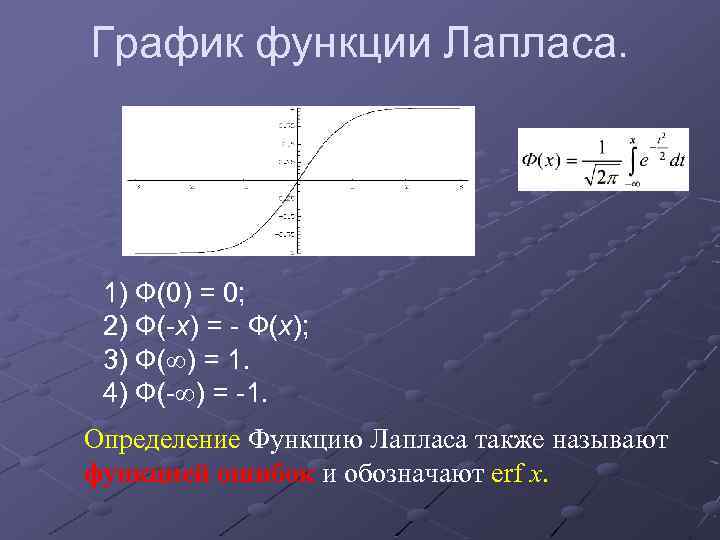График функции Лапласа. 1) Ф(0) = 0; 2) Ф( х) = Ф(х); 3) Ф( График функции Лапласа. 1) Ф(0) = 0; 2) Ф( х) = Ф(х); 3) Ф( ) = 1. 4) Ф( ) = 1. Определение Функцию Лапласа также называют функцией ошибок и обозначают erf x.

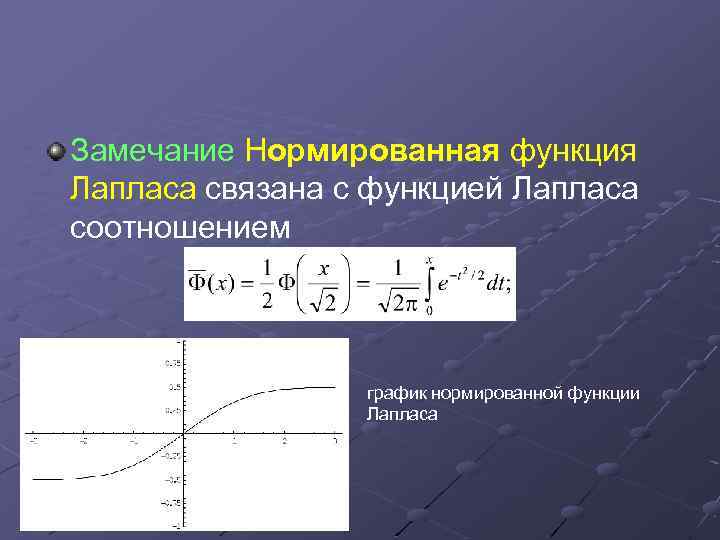Замечание Нормированная функция Лапласа связана с функцией Лапласа соотношением график нормированной функции Лапласа Замечание Нормированная функция Лапласа связана с функцией Лапласа соотношением график нормированной функции Лапласа

Вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины Вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины :

Для нормального закона верны формулы: Для нормального закона верны формулы:

Пример Средняя масса коробки конфет равна 540 г. Найти среднее отклонение от массы , Пример Средняя масса коробки конфет равна 540 г. Найти среднее отклонение от массы , если известно, что масса коробок распределена нормально и 5 % коробок имеют массу не большую 530 г. Решение

Вероятность попадания нормально распределенной случайной величины на заданный интервал Пример. Случайная величина Х Вероятность попадания нормально распределенной случайной величины на заданный интервал Пример. Случайная величина Х имеет нормальное распределение с параметрами а = 3, σ = 2. Найти вероятность того, что она примет значение из интервала (4, 8).

CВ подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Такая ситуация CВ подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Такая ситуация распространена, поэтому в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий. Нормальное распределение зависит от двух параметров — смещения и масштаба Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1 N(0, 1).

Числовые характеристики нормального распределения Числовые характеристики нормального распределения

Функция распределения Функция распределения

Замечание Функция распределения стандартной нормальной СВ X ~ N(0, 1), называется также функцией Лапласа Замечание Функция распределения стандартной нормальной СВ X ~ N(0, 1), называется также функцией Лапласа

Свойства функции Лапласа Свойства функции Лапласа

Если случайная величина имеет плотность распределения, выражающуюся функцией n(x; 0; 1), то есть – Если случайная величина имеет плотность распределения, выражающуюся функцией n(x; 0; 1), то есть – нормально распределённая случайная величина с математическим ожиданием, равным нулю, и дисперсией, равной единице, то

Замечание. Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что Замечание. Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что называют "правилом k сигм":

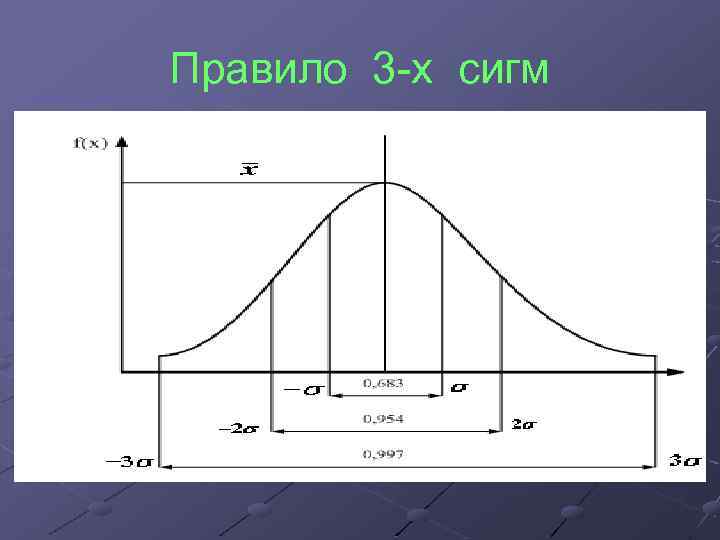Правило 3 х сигм Правило 3 х сигм

Величина Х (среднее арифметическое) показывает смещение кривой Х f(х) вдоль оси абсцисс без Величина Х (среднее арифметическое) показывает смещение кривой Х f(х) вдоль оси абсцисс без изменения ее формы, т. е. расстояние от начала координат до абсциссы с максимальной ординатой. величина (среднее квадратичное отклонение) показывает разброс отдельных значений случайной величины х относительно среднего арифметического. На участке кривой, ограниченной ординатами расположено 68, 3% значений случайной величины; на участке, ограниченном ординатами 2 , 95, 4%; на участке с ординатами 3 , 99, 7%. правило трех сигм: вероятность того, что случайная величина х лежит в пределах 3 , близка к единице или к 100%. Следовательно, значения случайной величины, лежащие за пределами 3 х сигм, можно отбросить как промахи

Правило 3 сигм Если случайная величина распределена нормально, то абсолютная величина ее отклонения Правило 3 сигм Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Замечание Нормальный закон наблюдается, когда на измеряемую СВ действуют разнообразные факторы, не связанные между Замечание Нормальный закон наблюдается, когда на измеряемую СВ действуют разнообразные факторы, не связанные между собой и равнозначно действующие на случайную величину Пример размеры и износы деталей, наработки на отказ и до предельного состояния, причинами которых являются износы и т. д. ).

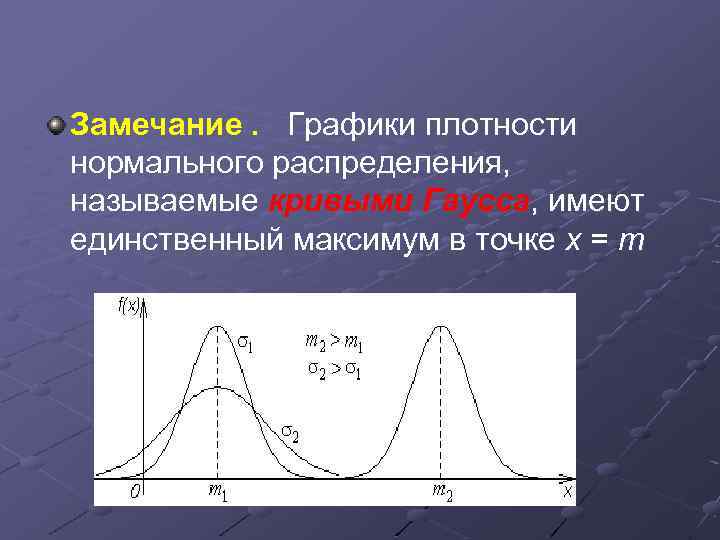Замечание. Графики плотности нормального распределения, называемые кривыми Гаусса, имеют единственный максимум в точке x Замечание. Графики плотности нормального распределения, называемые кривыми Гаусса, имеют единственный максимум в точке x = m

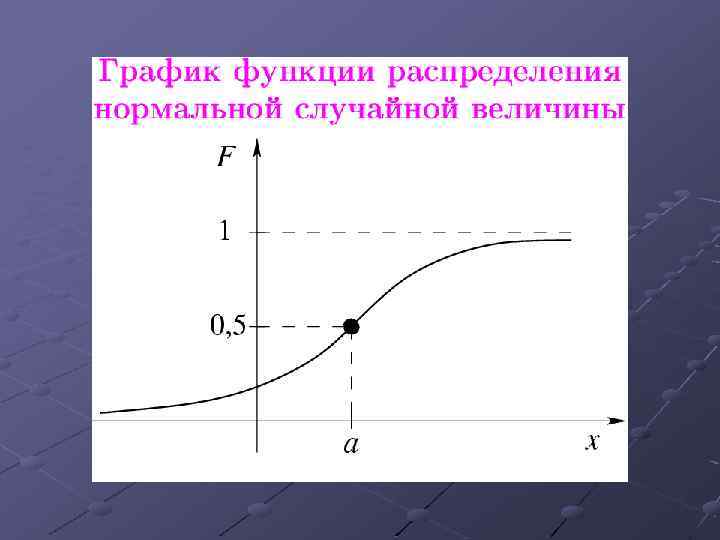
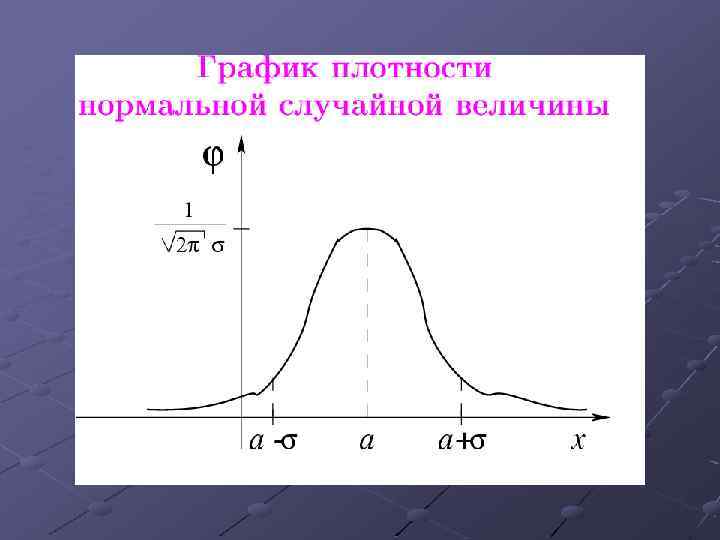
Замечание Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым Замечание Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым

Эксцесс (термин был впервые введен Пирсоном, 1905) или точнее, коэффициент эксцесса измеряет Эксцесс (термин был впервые введен Пирсоном, 1905) или точнее, коэффициент эксцесса измеряет "пикообразность" распределения. Если эксцесс значимо отличен от 0, то функция плотности либо имеет более закругленный , либо более острый пик, чем пик плотности нормального распределения. Функция плотности нормального распределения имеет эксцесс равный 0.

Числовые характеристики нормального распределения Асимметрия, эксцесс, мода и медиана нормального распределения равны: As(X) Числовые характеристики нормального распределения Асимметрия, эксцесс, мода и медиана нормального распределения равны: As(X) = 0; Ex(X) = 0; Mo(X) = a; Me(X) = a, где а математическое ожидание.