 Законы логики • Закон тождества • Закон непротиворечия • Закон исключённого третьего • Закон достаточного основания
Законы логики • Закон тождества • Закон непротиворечия • Закон исключённого третьего • Закон достаточного основания
 Законы формальной логики Наиболее простые и необходимые связи между мыслями выражаются в основных законах формальной логики. Таковыми являются законы тождества, непротиворечия, исключения третьего, достаточного основания. Эти законы позволяют упрощать логические выражения и строить умозаключения и доказательства. Первые три были выявлены и сформулированы Аристотелем, а закон достаточного основания – Г. Лейбницем.
Законы формальной логики Наиболее простые и необходимые связи между мыслями выражаются в основных законах формальной логики. Таковыми являются законы тождества, непротиворечия, исключения третьего, достаточного основания. Эти законы позволяют упрощать логические выражения и строить умозаключения и доказательства. Первые три были выявлены и сформулированы Аристотелем, а закон достаточного основания – Г. Лейбницем.
 Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе. а есть а или а = а (для суждений) А есть А или А = А (для понятий)
Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе. а есть а или а = а (для суждений) А есть А или А = А (для понятий)
 Закон непротиворечия • Закон непротиворечия: невозможно, чтобы одно и то же время было и не было присуще одному и тому же в одном и том же отношении. То есть невозможно что-либо одновременно утверждать и отрицать.
Закон непротиворечия • Закон непротиворечия: невозможно, чтобы одно и то же время было и не было присуще одному и тому же в одном и том же отношении. То есть невозможно что-либо одновременно утверждать и отрицать.
 Закон исключения третьего Закон исключенного третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано.
Закон исключения третьего Закон исключенного третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано.
 Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована.
Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована.
 Основные законы Закон тождества: А=А Всякое понятие и суждение тождественно самому себе. Закон непротиворечия: А&A = 1 или A&A = 0 Не могут быть одновременно истинными суждение и его отрицание Закон исключенного третьего: Аv. А = 1 В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Закон двойного отрицания: А=А Если отрицать дважды некоторое высказывание, то в результате получится исходное высказывание.
Основные законы Закон тождества: А=А Всякое понятие и суждение тождественно самому себе. Закон непротиворечия: А&A = 1 или A&A = 0 Не могут быть одновременно истинными суждение и его отрицание Закон исключенного третьего: Аv. А = 1 В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Закон двойного отрицания: А=А Если отрицать дважды некоторое высказывание, то в результате получится исходное высказывание.
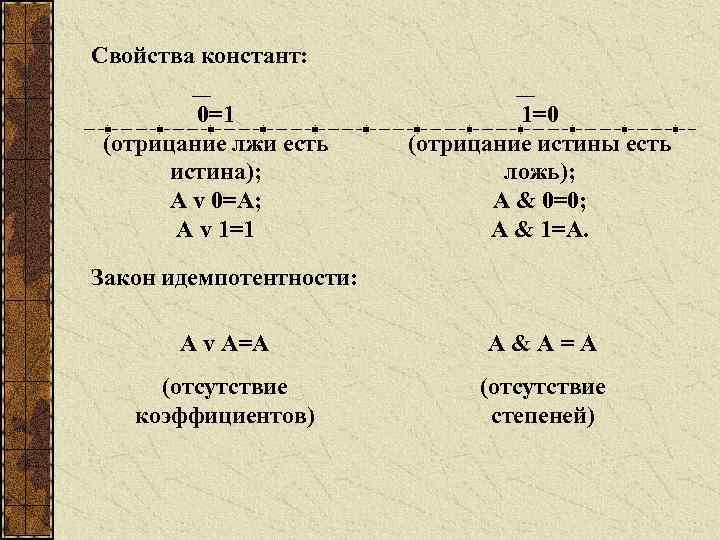 Свойства констант: 0=1 (отрицание лжи есть истина); A v 0=A; A v 1=1 1=0 (отрицание истины есть ложь); A & 0=0; A & 1=A. Закон идемпотентности: A v A=A A&A=A (отсутствие коэффициентов) (отсутствие степеней)
Свойства констант: 0=1 (отрицание лжи есть истина); A v 0=A; A v 1=1 1=0 (отрицание истины есть ложь); A & 0=0; A & 1=A. Закон идемпотентности: A v A=A A&A=A (отсутствие коэффициентов) (отсутствие степеней)
 Законы коммутативности: A v B=B v A; A & B=B & A Законы ассоциативности: A v (B v C) =(A v B) v C; A & (B & C)=(A & B)&C Законы дистрибутивности: A v (B & C)=(A v B) & (A v C); A & (B v C)=(A & B)v( A & C) Законы поглощения: Av(A&B)=A; A&(A v B)=A Законы де Моргана: Av. B=A&B A&B=Av. B
Законы коммутативности: A v B=B v A; A & B=B & A Законы ассоциативности: A v (B v C) =(A v B) v C; A & (B & C)=(A & B)&C Законы дистрибутивности: A v (B & C)=(A v B) & (A v C); A & (B v C)=(A & B)v( A & C) Законы поглощения: Av(A&B)=A; A&(A v B)=A Законы де Моргана: Av. B=A&B A&B=Av. B
 Правила замены операций импликации и эквивалентности А В = А v B; А В = B A; A B = ( A & B) v (A & B ); A B = ( A v B) & (A v B ); A B = ( A B) & (B A );
Правила замены операций импликации и эквивалентности А В = А v B; А В = B A; A B = ( A & B) v (A & B ); A B = ( A v B) & (A v B ); A B = ( A B) & (B A );