Закон поясов закон Вейса Этот закон позволяет выводить

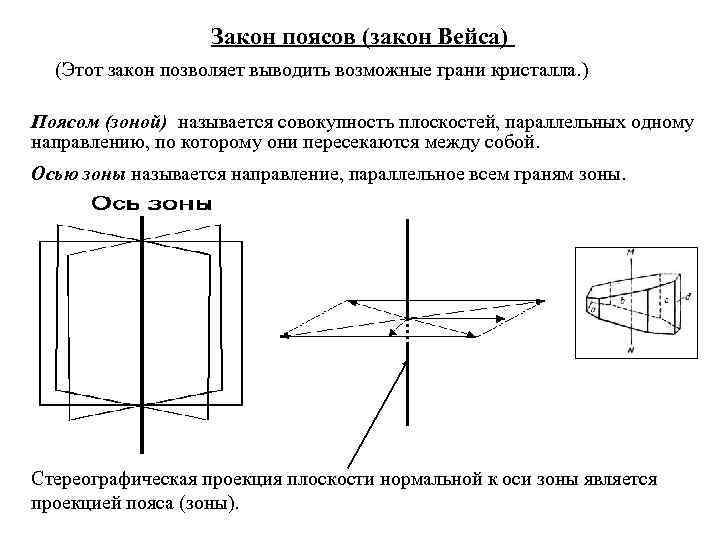Закон поясов (закон Вейса) (Этот закон позволяет выводить возможные грани кристалла. ) Поясом (зоной) называется совокупность плоскостей, параллельных одному направлению, по которому они пересекаются между собой. Осью зоны называется направление, параллельное всем граням зоны. Стереографическая проекция плоскости нормальной к оси зоны является проекцией пояса (зоны).

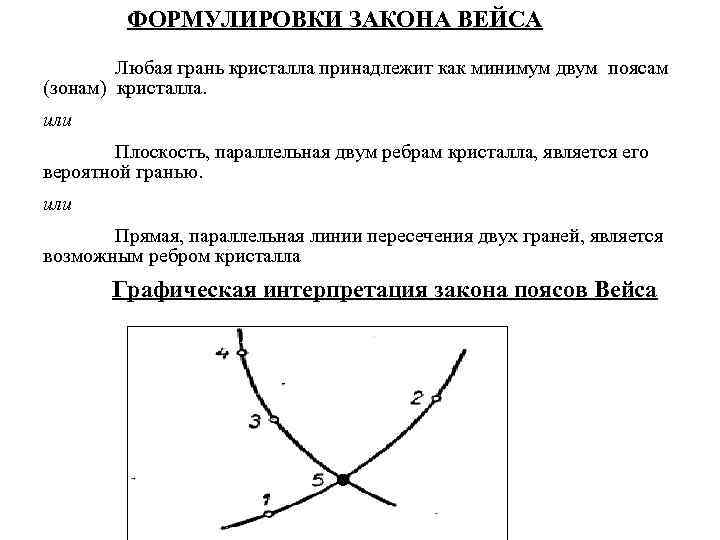ФОРМУЛИРОВКИ ЗАКОНА ВЕЙСА Любая грань кристалла принадлежит как минимум двум поясам (зонам) кристалла. или Плоскость, параллельная двум ребрам кристалла, является его вероятной гранью. или Прямая, параллельная линии пересечения двух граней, является возможным ребром кристалла Графическая интерпретация закона поясов Вейса

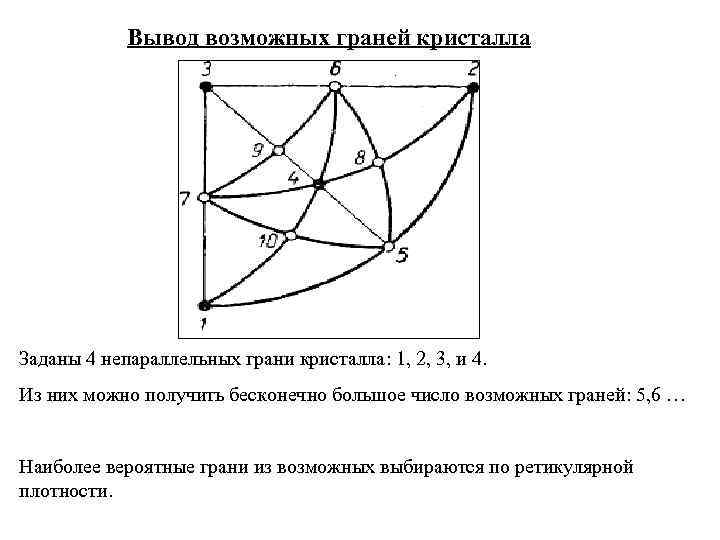Вывод возможных граней кристалла Заданы 4 непараллельных грани кристалла: 1, 2, 3, и 4. Из них можно получить бесконечно большое число возможных граней: 5, 6 … Наиболее вероятные грани из возможных выбираются по ретикулярной плотности.

Форма кристалла, простые формы. Абсолютно различные на вид многогранники могут принадлежать к одному и тому же виду симметрии. Например, куб и октаэдр обладают одним и тем же набором элементов симметрии. Каждой группе симметрии соответствует один или несколько многогранников, которые содержат все элементы симметрии входящие в группу. Простой формой кристалла называется многогранник, все грани которого получаются с помощью преобразований симметрии, входящих в точечную группу. Все грани простой формы кристаллографически равны. Одной точечной группе симметрии может соответствовать несколько простых форм. С другой стороны, одна простая форма может принадлежать разным группам. Куб, например, является простой формой всех классов кубической сингонии.

Общая и частная простые формы Общая простая форма получается, если исходная грань находится в произвольном положении относительно элементов симметрии, т. е. вне элементов симметрии (может быть только одна в точечной группе). Частная простая форма образуется, если исходная грань располагается перпендикулярно или параллельно осям или плоскостям симметрии, а также когда эта грань пересекает элементы симметрии под одинаковыми углами (может быть несколько). В октаэдре, например, грань пересекает все оси симметрии четвертого порядка под углом 45º.

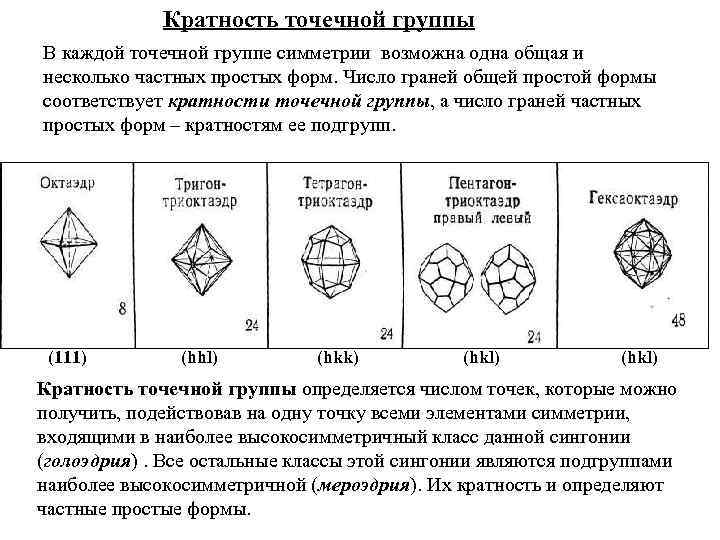Кратность точечной группы В каждой точечной группе симметрии возможна одна общая и несколько частных простых форм. Число граней общей простой формы соответствует кратности точечной группы, а число граней частных простых форм – кратностям ее подгрупп. (111) (hhl) (hkk) (hkl) Кратность точечной группы определяется числом точек, которые можно получить, подействовав на одну точку всеми элементами симметрии, входящими в наиболее высокосимметричный класс данной сингонии (голоэдрия). Все остальные классы этой сингонии являются подгруппами наиболее высокосимметричной (мероэдрия). Их кратность и определяют частные простые формы.

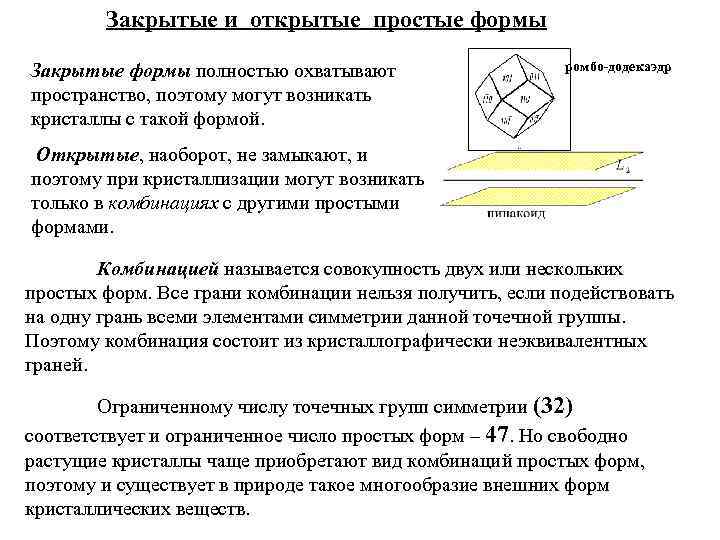Закрытые и открытые простые формы Закрытые формы полностью охватывают пространство, поэтому могут возникать кристаллы с такой формой. ромбо-додекаэдр Открытые, наоборот, не замыкают, и поэтому при кристаллизации могут возникать только в комбинациях с другими простыми формами. Комбинацией называется совокупность двух или нескольких простых форм. Все грани комбинации нельзя получить, если подействовать на одну грань всеми элементами симметрии данной точечной группы. Поэтому комбинация состоит из кристаллографически неэквивалентных граней. Ограниченному числу точечных групп симметрии (32) соответствует и ограниченное число простых форм – 47. Но свободно растущие кристаллы чаще приобретают вид комбинаций простых форм, поэтому и существует в природе такое многообразие внешних форм кристаллических веществ.

Образец типовой записи группы симметрии Порядок записи: Шеелит - . 1. Элементы симметрии. 1. 2. 3. Число единичных направлений и 2. Одно, совпадающее с осью 4. их расположение. 3. Тетрагональная, средняя. . Сингония и ее категория. 4. Название вида симметрии. 4. Центральный вид симметрии тетрагональн. с 5. Число простых форм. 5. Комбинация трех простых форм(a, b, c). 6. Подразделение форм на общие и 6. частные. 7. Названия простых форм. 8. Проекция. 7. 8. 9. Название вида симметрии по общей форме. 9. Все простые формы общие. Три тетрагональные дипирамиды. См. рис. Тетрагонально-дипирамидальный вид.