Закон электромагнитной индукции n n Индукция наведение —

Закон электромагнитной индукции n n Индукция (наведение) - возникновение одного поля (например, электрического) при изменении другого поля (например, магнитного). Электромагнитной индукцией называется явление возникновения электрического поля при изменении магнитного поля. Впервые это явление было открыто выдающимся английским физиком Майклом Фарадеем в 1831 г. n Фарадей установил, что индук- ционный ток возникает в замкнутом контуре при изменении во времени магнитного потока, пронизывающего этот контур. n -магнитный поток.

Знак «минус» показывает направление индукционного тока которое определяется правилом Э. Х. Ленца (1833 г. ) − индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока, вызывающего этот ток (R сопротивление контура). Если ЭДС индукции e(t) появляется вследствие возрастания магнитного потока Ф (внесение магнита в катушку), то индукционный ток создаст магнитное поле, уменьшающее возрастание Ф, т. е. будет стараться вытолкнуть магнит из катушки и наоборот.

n n Изменение магнитного потока пронизывающего замкнутый контур, может происходить по нескольким причинам. , Во-первых, вследствие изменения индукции магнитного поля, что наблюдалось в опытах Фарадея. Во вторых, при повороте контура в постоянном магнитном поле, т. е. при изменении угла α. Это наблюдается в электрогенераторах. В третьих, вследствие перемещения контура или его частей в постоянном магнитном поле.

n Рассмотрим возникновение ЭДС индукции в прямоугольном проводящем контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью υ по двум другим направляющим сторонам : d. S=υl dt 1 подход: За время dt площадь контура изменяется на d. S=υl dt, что соответствует изменению магнитного потока на dΦ=Bυldt. Тогда ЭДС индукции 2 подход: На свободные заряды движущегося участка контура длиной l действует сила Лоренца, направленная вдоль проводника: F=qυB. Под действием силы Лоренца свободные заряды перемещаются на расстояние l, при этом совершается работа A по перемещению заряда и возникает ЭДС индукции e A=Fl =q (-e), e = - A/q= - υBl.

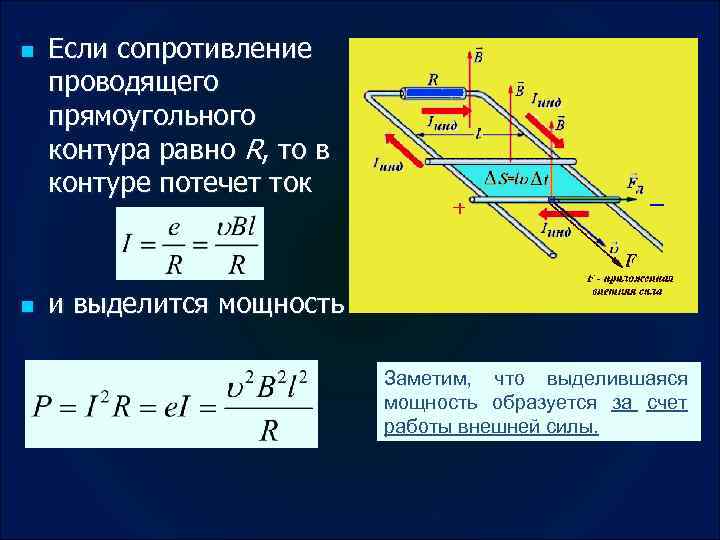n n Если сопротивление проводящего прямоугольного контура равно R, то в контуре потечет ток и выделится мощность Заметим, что выделившаяся мощность образуется за счет работы внешней силы.

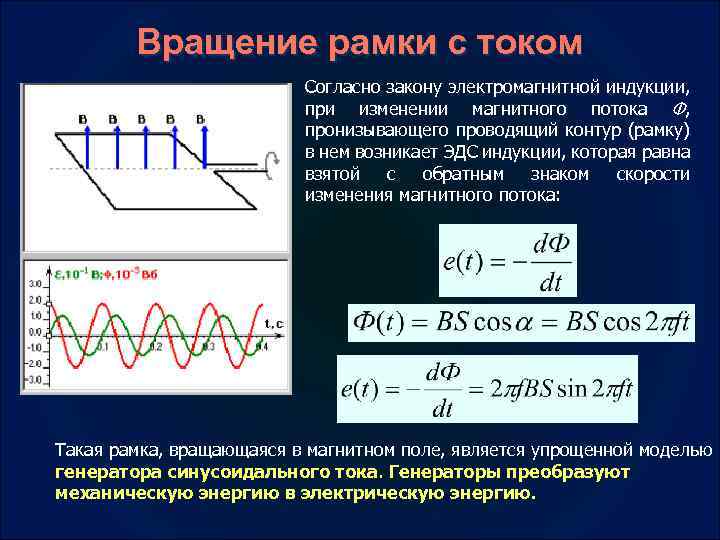Вращение рамки с током Согласно закону электромагнитной индукции, при изменении магнитного потока Ф, пронизывающего проводящий контур (рамку) в нем возникает ЭДС индукции, которая равна взятой с обратным знаком скорости изменения магнитного потока: Такая рамка, вращающаяся в магнитном поле, является упрощенной моделью генератора синусоидального тока. Генераторы преобразуют механическую энергию в электрическую энергию.

Явление самоиндукции. Индуктивность n n Если по замкнутому контуру протекает переменный ток i(t), то магнитное поле с изменяющимся потоком создается собственным током в этом контуре, и в соответствии с законом электромагнитной индукции, в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции равна взятой с обратным знаком скорости изменения потокосцепления Ψ(t)=N Ф(t): где N число витков контура, Ф поток, пронизывающий один виток.

n Потокосцепление Ψ пропорционально току i(t): n где L - индуктивность контура, зависящая от геометрии контура и числа витков N. В частности, индуктивность бесконечно длинного соленоида (катушки) и тороида сечением S с числом витков N и длиной l Здесь - u. L(t) - напряжение на индуктивности.

Токи при размыкании и замыкании электрической цепи Рассмотрим процесс замыкания цепи, которая состоит из последовательно включенных источника постоянной ЭДС E, резистора R и катушки индуктивности L: Этот процесс описывается законом Кирхгофа в дифференциальной форме: Полагая, что до коммутации ток в индуктивности был равен нулю, и, используя теорию обыкновенных дифференциальных уравнений, получим решение уравнения - постоянная времени цепи. Ток изменяется по экспоненциальному закону от нуля до стационарного значения E/R. ( рис а)).

Явление взаимной индукции. Взаимная индуктивность Явление взаимной Рассмотрим два неподвижных индукции заключается в контура 1 и 2, расположенных наведении ЭДС индукции во достаточно близко друг от друга с всех проводниках, числом витков N 1 и N 2, соответнаходящихся вблизи цепи ственно. переменного тока i(t). n Если в контуре 1 течет ток i 1(t), то магнитный поток, создаваемый этим током (этот поток на рис. - сплошные линии), пропорционален току i 1(t). Обозначим через Φ 12 ту часть потока, которая пронизывает контур 2. Тогда потокосцепление ψ12 = N 2 Φ 12, сцепленное со вторым контуром, равно:

n Если ток i 1(t) в первом контуре изменяется во времени, то в контуре 2 индуцируется ЭДС e 12(t), которая по закону Фарадея пропорциональна скорости изменения потокосцепления ψ12: n Аналогично, при протекании в контуре 2 переменного тока i 2(t) магнитный поток Φ 21 (- изображен пунктирными линиями), пронизывает первый контур. Тогда потокосцепление ψ21 = N 1Φ 21, сцепленное с первым контуром, равно: При этом в контуре 1 возникает ЭДС e 21(t), пропорциональная скорости изменения потокосцепления ψ21:

n n n Явление возникновения ЭДС в одном из контуров при изменении тока в другом контуре называется взаимной индукцией. Коэффициенты пропорциональности M 12 и M 21 называются коэффициентами взаимной индукции или взаимной индуктивностью. Расчеты, подтвержденные опытом, показывают, что эти коэффициенты равны другу , т. е. Взаимная индуктивность M зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей среды. Размерность взаимной индуктивности M такая же, как индуктивности L - 1 Гн.

n Рассчитаем в качестве примера взаимную индуктивность двух катушек, намотанных на общий тороидальный сердечник с магнитной проницаемостью µ: n n Магнитная индукция поля, создаваемого первой катушкой с числом витков N 1 и током i 1(t), согласно закону полного тока: n где l - длина сердечника по средней линии. Тогда потокосцепление, сцепленное со вторым контуром а взаимная индуктивность n В инженерной практике при расчете контуров с взаимной индуктивностью широко используется коэффициент связи k между магнитносвязанными катушками с индуктивностями L 1, L 2 и взаимной индуктивностью M

Рассмотрим теперь схему из двух последовательно включенных магнитносвязанных катушек с индуктивностями L 1, L 2 и взаимной индуктивностью M Магнитные поля первой и второй катушек, в зависимости от направления их намоток и направления токов, могут складываться, а могут и вычитаться. Случай, когда магнитные поля складываются, называется согласным включением катушек. Одноименные концы катушек помечают точками или звездочками. Если токи катушек одинаково направлены относительно одноименных зажимов, то имеет место согласное включение (рис. а)). Случай, когда магнитные поля катушек вычитаются, называется встречным включением катушек (рис. 1 б)).

Напряжение u 1(t) и u 2(t) на каждой из магнитносвязанных катушек состоит из двух компонент: напряжения самоиндукции, и напряжения взаимной индукции. Знак плюс соответствует согласному включению, знак минус – встречному включению катушек. Рассмотрим включение двух магнитносвязанных катушек при синусоидальном воздействии

Решение уравнения имеет вид: При встречном включении катушек в формуле следует перед членом 2 M поставить знак минус.

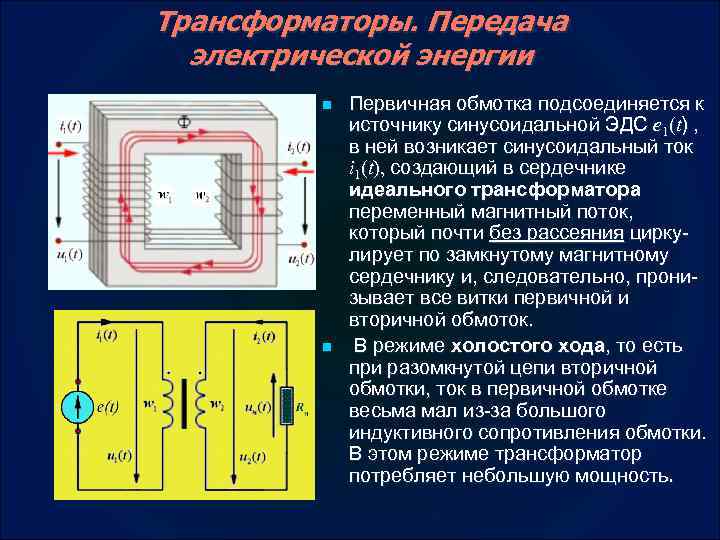Трансформаторы. Передача электрической энергии n n Первичная обмотка подсоединяется к источнику синусоидальной ЭДС e 1(t) , в ней возникает синусоидальный ток i 1(t), создающий в сердечнике идеального трансформатора переменный магнитный поток, который почти без рассеяния цирку лирует по замкнутому магнитному сердечнику и, следовательно, прони зывает все витки первичной и вторичной обмоток. В режиме холостого хода, то есть при разомкнутой цепи вторичной обмотки, ток в первичной обмотке весьма мал из за большого индуктивного сопротивления обмотки. В этом режиме трансформатор потребляет небольшую мощность.

n Когда в цепь вторичной обмотки включают сопротивление нагрузки Rн, то в ней возникает синусоидальный ток i 2(t). Теперь полный магнитный поток в сердечнике созданный обоими токами i 1(t) и i 2(t). n Согласно правилу Ленца, магнитный поток Φ 2(t), создаваемый индуцированным во вторичной обмотке током i 2(t), направлен навстречу потоку Φ 1(t), создаваемому током i 1(t) в первичной обмотке. Отсюда следует, что токи i 1(t) и i 2(t) изменяются в противофазе, то есть имеют фазовый сдвиг, равный 180°. n n n Как правило, ток i 1(t) в первичной обмотке в режиме нагрузки значительно больше тока холостого хода i 1 x(t). Это следует из того, что полный магнитный поток Φ идеального трансформатора в сердечнике должен быть в режиме нагрузки таким же, как и в режиме холостого хода. При этом напряжение u 1(t) на первичной обмотке в обоих случаях одно и то же. Это напряжение равно ЭДС источника e 1(t) переменного тока. Потокосцепления ψ = NΦ= wΦ, пронизывающие обмотки, пропорциональны числу w 1 и w 2 витков в них, поэтому можно записать:

n Следовательно, n n n (*) где k. ТР - коэффициент трансформации. При w 2> w 1 трансформатор называется повышающим, при w 2< w 1– понижающим. Написанные выше соотношения, строго говоря, применимы только к идеальному трансформатору, в котором нет рассеяния магнитного потока, и отсутствуют тепловые потери. Эти потери могут быть связаны с наличием активных сопротивлений R 1, R 2 самих обмоток и возникновением индукционных токов Фуко в сердечнике. У современных трансформаторов потери энергии при нагрузках, близких к номинальным нагрузкам, не превышают 1– 2 %. Поэтому к ним приближенно применима теория идеального трансформатора.

n Для идеального трансформатора отношение токов в обмотках обратно пропорционально числу витков: n (**) Здесь знак минус учитывает сдвиг фаз 180° между токами i 1(t) и i 2(t) . Комбинируя соотношения (*), (**) и учитывая формулу получим __________________________ Для уменьшения потерь на нагревания проводов необходимо уменьшить силу тока в линии передачи, следовательно, увеличить напряжение. Обычно линии электропередачи строятся в расчете на напряжение 400– 500 к. В, при этом в линиях используется трехфазный ток частотой 50 Гц. Коэффициент полезного действия линии передач не превышает 90 %.

Вихревые токи Фуко Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми. Их так же называюттоками Фуко. n Токи Фуко, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Например, если между полюсами электромагнита 1 массивный медный маятник 2 совершает практически незатухающие колебания , то при включении тока он испытывает сильное торможение и быстро останавливается.

n Вихревые токи помимо торможения (как правило, нежелательного эффекта) вызывают нагревание проводников. Поэтому для уменьшения потерь на нагревание якоря генераторов и сердечники трансформаторов делают не сплошными, а изготовляют из тонких пластин, отделенных одна от другой слоями изолятора, и устанавливают их так, чтобы вихревые токи были направлены поперек пластин.

Энергия магнитного поля n n Магнитное поле, подобно электрическому полю, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. Рассмотрим контур с индуктивностью L, по которому течет ток i. С контуром сцеплено магнитное потокосцепление ψ=Li, причем при изменении тока на di потокосцепление изменяется на dψ=Ldi. Для изменения магнитного потокосцепления на dψ необходимо совершить работу d. A=e i dt. Подставив n n d. A=i dψ =Lidi; Тогда работа, равная энергии магнитного поля

n Рассмотрим магнитное поле внутри длинного соленоида сечением S с числом витков N и длиной l где n=N/l - число витков на единицу длины, V - объем соленоида, получим для соленоида: - объемная плотность энергии.