Закон Архимеда На тело погружённое в жидкость

Закон Архимеда

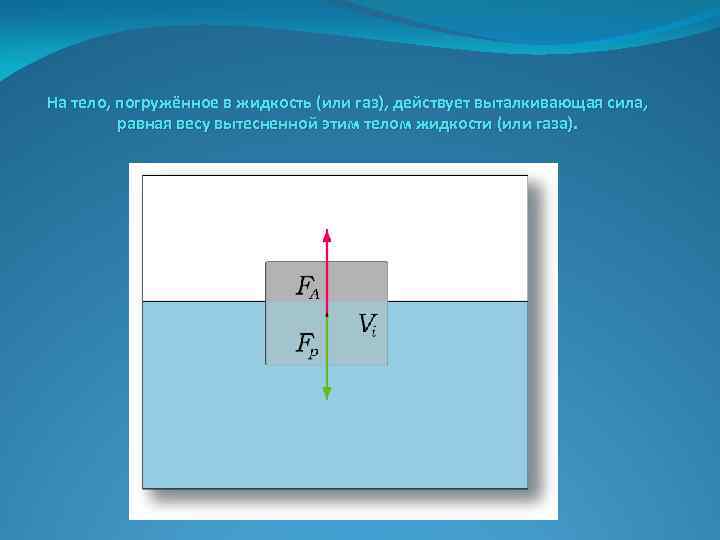На тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа).

Сила, действующая на погруженное тело, называется силой Архимеда FА=ρg. V где ρ — плотность жидкости (газа), g — ускорение свободного падения, а V — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Вывод закона Архимеда для тела произвольной формы Гидростатическое давление жидкости на глубине h есть p=ρgh. При этом считаем давление жидкости и напряжённость гравитационного поля постоянными величинами, а h — параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxzy , причём выберем направление оси z совпадающим с направлением вектора. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку d. S. На неё будет действовать сила давления жидкости направленная внутрь тела, d. FА. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности: При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса Получаем, что модуль силы Архимеда равен ρg. V , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Условие плавания тел Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести и силы Архимеда , которые действуют на это тело. Возможны следующие три случая: Fт>FА – тело тонет, Fт=FА – тело плавает в жидкости или газе Fтρs - тело тонет ρт=ρs - тело плавает в жидкости или газе ρт<ρs - тело всплывает до тех пор, пока не начнёт плавать.