Задания ЕГЭ Часть 5 Задания 20 Анализ программы

Задания ЕГЭ. Часть 5 Задания 20. Анализ программы с циклами и условными операторами Задания 21. Анализ программ с циклами и подпрограммами Задания 22. Оператор присваивания и ветвления. Перебор вариантов, построение дерева Задания 23. Логические уравнения Задания 24 (С 1). Поиск и исправление ошибок в программе. Задания 25 (С 2). Алгоритмы обработки массивов

20 3 По лу чив на вход число x, этот ал го ритм пе ча та ет два числа a и b. Ука жи те наи мень шее из таких чисел x, при вводе ко то ро го ал го ритм пе ча та ет сна ча ла 2, а потом 13.

20 3 решение Рас смот рим цикл, число шагов ко то ро го за ви сит от из ме не ния пе ре мен ной x: while x > 0 do begin. . . x: = x div 100; end; Т. к. опе ра тор div воз вра ща ет целую часть от де ле ния, то при де ле нии на 100 это рав но силь но от се че нию по след них двух цифр. На каж дом шаге от де ся тич ной за пи си x от се ка ет ся две по след них цифры до тех пор, пока все цифры не будут от се че ны, то есть x не ста нет равно 0. Для того, чтобы a стало рав ным 2, долж но быть трёхзнач ным x или четырёхзнач ным. Те перь рас смот рим из ме не ние b: while x>0 do begin b: =b+(x mod 100); end; Опе ра тор mod воз вра ща ет оста ток от де ле ния, при де ле нии на 100 это по след ние две цифры x. Разобьём 13 на два сла га е мых так, чтобы можно было со ста вить трёхзнач ное число: 13 = 1 +12. Ис ко мое число — 112.

20 4 По лу чив на вход число x, этот ал го ритм пе ча та ет число M. Из вест но, что x > 100. Ука жи те наи мень шее такое (т. е. боль шее 100) число x, при вводе ко то ро го ал го ритм пе ча та ет 26.

20 4 Решение В теле цикла числа M и L умень ша ют ся, пока не ста нут рав ны ми. Чтобы в итоге было на пе ча та но 26, оба числа в какой то мо мент долж ны быть равны 26. Пой дем т конца к на ча лу: на преды ду щем шаге одно о число было 26, а дру гое 26 + 26 = 52. Еще на шаг рань ше 52 + 26 = 78 и 52. До того 78 + 52 = 130 и 52. То есть наи мень шее воз мож ное число 130. А по сколь ку най ден ное число чет ное, то M будет при сво е но зна че ние 52, что и при ве дет к не об хо ди мо му ре зуль та ту. Ответ: 130.

21 1 Опре де ли те, какое число будет на пе ча та но в ре зуль та те вы пол не ния сле ду ю ще го ал го рит ма: Var a, b, t, M, R : integer; Function F(x: integer): integer; begin F: =(x+5)*(x+3); end; BEGIN a: = 5; b: =5; M: =a; R: =F(a); for t: =a to b do begin if (F(t)> R)then begin M: =t; R: =F(t); end; write(R); END.

21 1 решение • 1. Ал го ритм пред на зна чен для по ис ка наи боль ше го зна че ния функ ции F(t) на от рез ке от a до b. • 2. F(x)=(x+5)(x+3) Квад рат ный трех член F(t) по ло жи тель ным стар шим ко эф фи ци ен то пе ре се ка ет ось абс цисс в точ ках 5 и 3 и, сле до ва тель но, воз рас та ет на луче ( 4; ∞). По это му наи боль шее зна че ние функ ции до сти га ет ся в точке 5 и равно F(5)=80.

21 2 • На пи ши те в от ве те число раз лич ных зна че ний вход ной пе ре мен ной k, при ко то рых про грам ма выдаёт тот же ответ, что и при вход ном зна че нии k = 55. • Зна че ние k = 55 также вклю ча ет ся в подсчёт раз лич ных зна че ний k.

21 2 решение Про грам ма вы во дит ми ни маль ное , ко то рое удо вле тво ря ет не ра вен ству Найдём все под хо дя щие k. Это те k, для ко то рых вы пол не ны оба не ра вен ства Таким об ра зом по лу ча ем. Этот про ме жу ток со дер жит 27 целых зна че ний.

21 3 На пи ши те в от ве те число раз лич ных зна че ний вход ной пе ре мен ной k, при ко то рых про грам ма выдаёт тот же ответ, что и при вход ном зна че нии k = 55. Зна че ние k = 55 также вклю ча ет ся в подсчёт раз лич ных зна че ний k.

21 3 решение Про грам ма на хо дит ми ни маль ное i такое, чт вы пол ня ет ся не ра вен ство При. Найдём все под хо дя щие k. Это те k, для ко то рых вы пол не ны оба не ра вен ства Таким об ра зом по лу ча ем. Этот про ме жу ток со дер жит 18 целых зна че ний k.

21 4 При каком наи мень шем зна че нии вход ной пе ре мен ной k про г рам ма выдаёт тот же ответ, что и при вход ном зна че нии k = 64? .

21 4 решение Про грам ма вы во дит мак си маль ное I не боль ше 12, ко то рое удо вле тво ря ет не ра вен ству. Для для Таким об ра зом ми ни маль ное k — 62.

21 5 Опре де ли те, какое число будет на пе ча та но в ре зуль та те вы пол не ния сле ду ю ще го ал го рит ма: Var a, b, t, M, R : integer; Function F(x: integer): integer; begin F: =4*(x 5)*(x+3); end; BEGIN a: = 20; b: =20; M: =a; R: =F(a); for t: =a to b do begin if (F(t)< R)then begin M: =t; R: =F(t); end; write(R); END.

21 5 решение 1. Ал го ритм пред на зна чен для по ис ка наи мень ше го зна че ния функ ции F(t) на от рез ке от a до b. 2. Квад рат ный трех член F(t) с по ло жи тель ным стар шим ко эф фи ци ен том пе ре се ка ет ось абс цисс в точ ках 5 и − 3 и, сле до ва тель но, наи мень шее зна че ние до сти га ет ся в вер ши 1 и равно F(1) = − 64.

22 1 • Опре де ли те зна че ние суммы це ло чис лен ных пе ре мен ных и после вы пол не ния фраг мен та про грам мы:

22 1 • 28

22 2 Опре де ли те зна че ние пе ре мен ной "с" после вы пол не ния сле ду ю ще го фраг мен та про грам мы: x: = 8 + 2*5; y: = (x mod 10) + 14; x: = (y div 10) + 3; c: = x y;

22 2 решение • 17

22 3 У ис пол ни те ля Каль ку ля тор две ко ман ды, ко то рым при сво е ны но ме ра: 1. при бавь 2, 2. умножь на 5. Пер вая из них уве ли чи ва ет число на экра не на 2, вто рая — уве ли чи ва ет его в 5 раз. Про грам ма для Каль ку ля то ра — это по сле до ва тель ность ко манд. Сколь ко есть про грамм, ко то рые число 2 пре об ра зу ю в число 50?

22 3 решение 1. Если n не де лит ся на 10, то тогда R(n) = R(t(n)), так как су ще ству ет един ствен ный спо соб по лу че ния n из t(n) — при бав ле ни ем двоек. 2. Пусть n де лит ся на 5. Тогда R(n) = R(n / 5) + R(n 2)= R(n / 5) + R(n 10) (если n > 10). При n = 10 R(n) = 2 (два спо со ба: при бав ле ни ем четырёх двоек или од но крат ным умно же ни ем на 5). По это му до ста точ но по сте пен но вы чис лить зна че ния R(n) для всех чисе крат ных де ся ти и не пре вос хо дя щих 50: сна ча ла вы чис ля ем R(2), затем R(10), R(20) и т. д. Имеем: R(2) = 1 = R(4) = R(6) = R(8), R(10) = 2 = R(2) + R(8), R(20) = R(4) + R(10) =1 + 2 = 3 = R(22) = R(28), R(30) = R(6) + R(20) =1 + 3 = 4 = R(32) = R(38), R(40) = R(8) + R(30) =1 + 4 = 5 = R(42) = R(48), R(50) = R(10) + R(40) = 2 + 5 = 7. Ответ: 7.

22 3 решение 2 Если число на пять де лит ся, то ва ри ан тов по след ней ко ман ды два: при бавь 2 и умножь на 5, тогда . За пол ним со от вет ству ю щую таб ли цу по при ведёным фор му лам слева на пра во: При этом ячей ки, от но ся щи е ся к чис лам, ко то рые не де лят ся на 5, можно в ре ше нии и опу стить (за ис клю че ни ем пер во го числа):

22 4 У ис пол ни те ля Каль ку ля тор две ко ман ды, ко то рым при сво е ны но ме ра: 1. при бавь 2, 2. умножь на 3. Пер вая из них уве ли чи ва ет число на экра не на 2, вто рая — уве ли чи ва ет его в 3 раза. Про грам ма для Утро и те ля — это по сле до ва тель ность ко манд. Сколь ко есть про грамм, ко то рые число 1 пре об ра зу ют в число 25? Ответ обос нуй те.

22 4 решение Верны сле ду ю щие со от но ше ния: 1. Если n не де лит ся на 3, то тогда R(n) = R(t(n)), так как су ще ству ет един ствен ный спо соб по лу че ния n из t(n) — при бав ле ни ем двое 2. Пусть n де лит ся на 3. Тогда R(n) = R(n / 3) + R(n 2)= R(n / 3) + R(n 6) (если n > 6). При n = 3 R(n)) = 2 (два спо со ба: при бав ле ни ем двоек или од но крат ным умно же ни ем на 3). По это му до ста точ но по сте пен но вы чис лить зна че ния R(n) для в чисел, крат ных 3 и не пре вос хо дя щих 25: сна ча ла вы чис ля ем R(1) затем R(3), R(9) и т. д. Имеем: R(1) = 1 R(3) = 2 = R(1) + R(1), R(9) = R(3) + R(7) = 2 + 2 = 4 = R(11) = R(13), R(15) = R(5) + R(13) = 2 + 2 = 4 = R(17) = R(19), R(21) = R(7) + R(19) = 2 + 6 = 8 = R(23) = R(25). Ответ: 8

22 5 У ис пол ни те ля Каль ку ля тор две ко ман ды, ко то рым при сво е ны но ме ра: 1. при бавь 3, 2. умножь на 3. Пер вая из них уве ли чи ва ет число на экра не на 3, вто рая — уве ли чи ва ет его в 3 раз. Про грам ма для Утро и те ля — это по сле до ва тель ность ко манд. Сколь ко есть про грамм, ко то рые число 6 пре об ра зу ют в число 72? Ответ обос нуй те.

22 5 решение 1. Если n не де лит ся на 9, то тогда R(n) = R(t(n)), так как су ще ству ет един ствен ный спо соб по лу че ния n из t(n) — при бав ле ни ем троек. 2. Пусть n де лит ся на 9. Тогда R(n) = R(n / 3) + R(n 3)= R(n / 3) + R(n 9) (если n > 9). При n = 9 R(n)) = 1 (один спо соб: при бав ле ни ем трой ки). По это му до ста точ но по сте пен но вы чис лить зна че ния R(n) для всех чисел, крат ных 9 и не пре вос хо дя щих 72: сна ча ла вы чис ля ем R(6), затем R(9), R(18) и т. д. Имеем: R(6)=1 R(9) = 1 = R(12) = R(15), R(18) = R(6)+R(9)=1+1=2= R(21)=R(24), R(36) = R(12) + R(27) =1 + 3 = 4 = R(39) = R(42), R(45) = R(15) + R(36) =1 + 4 = 5= R(48) = R(51), R(54) = R(18) + R(45) =1 + 4 = 5= R(48) = R(51), R(63) = R(21) + R(54) =2 + 7 =9= R(66) = R(69), R(72) = R(24) + R(63) =2 + 9 = 11. Ответ: 11

22 4 У ис пол ни те ля Утро и тель две ко ман ды, ко то рым при сво е ны но ме ра: 1. при бавь 1, 2. умножь на 3. Пер вая из них уве ли чи ва ет число на экра не на 1, вто рая — утра и ва ет его. Про грам ма для Утро и те ля — это по сле до ва тель нос ко манд. Сколь ко есть про грамм, ко то рые число 4 пре об ра зу ют в число 34? Ответ обос нуй те.

22 4 решение Тогда R(n) = R(n / 3) + R(n 1)= R(n / 3) + R(n 3) (если n > 3). При n = 9 R(n)) = 1 (один спо соб: при бав ле ни ем трой ки). По это му до ста точ но по сте пен но вы чис лить зна че ния R(n) для в чисел, крат ных 3 и не пре вос хо дя щих 34: сна ча ла вы чис ля ем R(4) затем R(6), R(9) и т. д. Имеем: R(4)=1 R(6) = R(9)=1 = R(5) = R(10)= R(11), R(12) = R(4)+R(9)=1+1=2= R(13)=R(14), R(15) = R(5) + R(12) =1 + 2 = 3= R(16) = R(17), R(18) = R(6) + R(15) =1 + 3 = 4= R(19) = R(20), R(21) = R(7) + R(18) =1 + 4 = 5= R(22) = R(23), R(24) = R(8) + R(21) =1 + 5 =6= R(25) = R(26), R(27) = R(9) + R(24) =1 + 6 =7= R(28) = R(29), R(30) = R(9) + R(27) =1 + 7 =8= R(31) = R(32), R(33) = R(10) + R(30) =1 + 8 =9= R(34). Ответ: 9

22 5 У ис пол ни те ля Каль ку ля тор две ко ман ды: 1. при бавь 2 2. умножь на 3. Пер вая из них уве ли чи ва ет число на экра не на 2, вто рая — утра и ва ет его. Сколь ко раз лич ных чисел можно по лу чить из числа 2 с по мо щью про грам мы, ко то рая со дер жит ровно 3 ко ман ды?

22 5 решение С по мо щью одной ко ман ды из числа 2 можно по лу чить 2 раз лич ных числа: 2 + 2 = 4, 2 * 3 = 6. С по мо щью двух ко манд можно по лу чить по два числа из 4 и 6: 4 + 2 = 6, 4 * 3 = 12, 6 + 2 = 8, 6 * 3 = 18. С по мо щью трёх ко манд по лу ча ют ся сле ду ю щие числа. 12 + 2 = 14, 12 * 3 = 36, 8 + 2 = 10, 8 * 3 = 24, 18 + 2 = 20, 18 * 3 = 54, Число 6 даст числа 8 и 18. Итого: 8 чисел.

22 6 У ис пол ни те ля Каль ку ля тор две ко ман ды: 1. умножь на 2 2. умножь на 3. Пер вая из них умно жа ет число на экра не на 2, вто рая — утра и ва ет его. Сколь ко аз лич ных чисел можно по лу чить из р числа 2 с по мо щью про грам мы, ко то рая со дер жит ровно 3 ко ман ды?

22 6 решение С по мо щью одной ко ман ды из числа 2 можно по лу чить 2 раз лич ных числа: 2 * 2 = 4 2 * 3 = 6. С по мо щью двух ко манд можно по лу чить по два числа из 4 и 6: 4 * 2 = 8 4 * 3 = 12 6 * 2 = 12 6 * 3 = 18 Видим, что два ре зуль та та сов па да ют, по это му по лу чи лось 3 числа, а не 4. С по мо щью трёх ко манд по лу ча ют ся сле ду ю щие числа. 12 * 2 = 24 12 * 3 = 36 8 * 2 = 16 8 * 3 = 24 18 * 2 = 36 18 * 3 = 54 Числа 36 и 24 встре ча ют ся два жды, по это му всего по лу ча ем 4 раз лич ных числа. Ответ: 4.

23 1 Сколь ко су ще ству ет раз лич ных на бо ров зна че ний ло ги че ских пе ре мен ных x 1, х2, х. З, х4, х5, хб, х7, х8, ко то рые удо вле тво ря ют всем пе ре чис лен ным ниже усло ви ям? (x 1 —> х2) —> (х. З—> х4) = 1 (х. З —> х4) —> (х5 —> хб) = 1 (х5 —> хб) —> (х7 —> х8) = 1 В от ве те не нужно пе ре чис лять все раз лич ные на бо ры зна че ний пе ре мен ных x 1, х2, х. З, х4, х5, хб, х7, х8, при ко то рых вы пол не на дан ная си сте ма ра венств. В ка че ств от ве та Вам нужно ука зать ко ли че ство таких на бо ров.

23 1 Сделаем за ме ну переменных : (x 1 —> х2) = y 1; (х. З—> х4) = y 2; (х5 —> хб) = y 3; (х7 —> х8) = y 4. Тогда можно за пи сать си сте му в виде од но го уравнения : (y 1 —> y 2) ∧ (y 2 —> y 3) ∧ (y 3 —> y 4) = 1. y 1 0 0 1 y 2 0 0 0 1 1 y 3 0 0 1 1 + 3 + 9 + 27 + 81 = 121 y 4 0 1 1 y 1 y 2 y 3 y 4 вариант ов 0 0 1· 1· 1· 1 =1 0 0 0 1 1· 1· 1· 3 =3 0 0 1 1 1· 1· 3· 3 =9 0 1 1· 3· 3· 3 = 27 1 1 3· 3· 3· 3 = 81

23 2 Сколь ко су ще ству ет раз лич ных на бо ров зна че ний ло ги че ских пе ре мен ных x 1, х2, х. З, х4, х5, хб, х7, х8, x 9, x 10 ко то рые удо вле тво ря ют всем пе ре чис лен ным ниже усло ви ям? (x 1 —> х2) —> (х. З—> х4) = 1 (х. З —> х4) —> (х5 —> хб) = 1 (х5 —> хб) —> (х7 —> х8) = 1 (х7 —> х8) —> (х9 —> х10) = 1 В от ве те не нужно пе ре чис лять все раз лич ные на бо ры зна че ний пе ре мен ных x 1, х2, х. З, х4, х5, хб, х7, х8, x 9, x 10 при ко то рых вы пол не на дан ная си сте ма ра венств. В ка че стве от ве та Вам нужно ука зать ко ли че ство таких на бо ров.

23 2 • 1 + 3 + 9 + 27 + 81 + 243 = 364.

23 3 Сколь ко су ще ству ет раз лич ных на бо ров зна че ний ло ги че ских пе ре мен ных x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8 ко то ры удо вле тво ря ют всем пе ре чис лен ным ниже усло ви ям? (x 1≡x 2)—>(x 2≡x 3) = 1 (x 2≡x 3)—>(x 3≡x 4) = 1. . . (x 6≡x 7)—>(x 7≡x 8) = 1 В от ве те не нужно пе ре чис лять все раз лич ные на бо ры зна че ний пе ре мен ных x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8 при ко то рых вы пол не на дан ная си сте ма ра венств. В ка че ств от ве та Вам нужно ука зать ко ли че ство таких на бо ров.

23 3 решение За пи шем пе ре мен ные в строч ку: x x 4 x 5 x 6 x 7 x 8. Им пли ка ция 1 x 2 x 3 ложна толь ко в том слу чае, когда из ис ти ны сле ду ет ложь. Усло вие не вы пол ня ет ся, если в ряду после пары оди на ко вых цифр при сут ству ет дру гая цифра. На при мер, « 11101. . . » , что озна ча ет не вы пол не ние вто ро го усло вия. Рас смот рим ком би на ции пе ре мен ных, удо вле тво ря ю щие всем усло ви ям. Вы пи шем ва ри ан ты, при ко то рых все цифры че ре ду ют ся, таких два: 1010 и 0101. Те перь для пер во го ва ри ан та, на чи ная с конца, будем уве ли чи вать ко ли че ство по вто ря ю щих ся под ряд цифр (на столь ко, на сколь ко это воз мож Вы пи шем по лу чен ные ком би на ции: « 1010 1011; 1010 1111; 1011 1111; 1010 1000; 1010 0000; 1000 0000; 0000» таких ком би на ций де вять, вклю чая ис ход ную. Ана ло гич но для вто ро го ва ри ан та: « 0101; 0101 0100; 0101 0000; 0100 0000; 0101 0111; 0101 1111; 0111 1111; 1111» — таких ком би на ций также де вять. За ме тим, что ком би на ции 0000 и 1111 учте ны два жды. Таким об ра зом, по лу ча ем 9 + 9 − 2 = 16 ре ше ний.

23 4 Сколь ко су ще ству ет раз лич ных на бо ров зна че ний ло ги че ских пе ре мен ных x 1, x 2, x 3, x 4, x 5, x 6, x 7, ко то рые удо вле тво ря ют всем пе ре чис лен ным ниже усло ви ям? (x 1≡x 2)—>(x 2≡x 3) = 1 (x 2≡x 3)—>(x 3≡x 4) = 1. . . (x 5≡x 6)—>(x 6≡x 7) = 1 В от ве те не нужно пе ре чис лять все раз лич ные на бо ры зна че ний пе ре мен ных x 1, x 2, x 3, x 4, x 5, x 6, x 7, при ко то рых вы пол не на дан ная си сте ма ра венств. В ка че стве от ве та Вам нужно ука зать ко ли че ство таких на бо ров.

23 4 решение • 8+8 2=14

23 5 Сколь ко су ще ству ет раз лич ных на бо ров зна че ний ло ги че ских пе ре мен ных x 1, x 2, . . . x 8, ко то рые удо вле тво ря ют всем пе ре чис лен ным ниже усло ви я ((x 1 ≡ x 2) ∨ (x 3 ≡ x 4)) ∧ (¬(x 1 ≡ x 2) ∨ ¬(x 3 ≡ x 4)) = 1 ((x 3 ≡ x 4) ∨ (x 5 ≡ x 6)) ∧ (¬(x 3 ≡ x 4) ∨ ¬(x 5 ≡ x 6)) = 1 ((x 5 ≡ x 6) ∨ (x 7 ≡ x 8)) ∧ (¬(x 5 ≡ x 6) ∨ ¬(x 7 ≡ x 8)) = 1 В от ве те не нужно пе ре чис лять все раз лич ные на бо ры зна че ний пе ре мен ных x , … x 8 при ко то рых 1, x 2 вы пол не на дан ная си сте ма ра венств. В ка че стве от ве та Вам нужно ука зать ко ли че ство таких на бо ров.

23 5 решение • По стро им древо ре ше ний пер во го урав не ния За ме тим, что вы ра же ние (x 4) в двух слу ча ях равно 1 и в 3 ≡ x двух слу ча ях равно 0. Таким об ра зом, одно урав не ние имеет во семь ре ше ний.

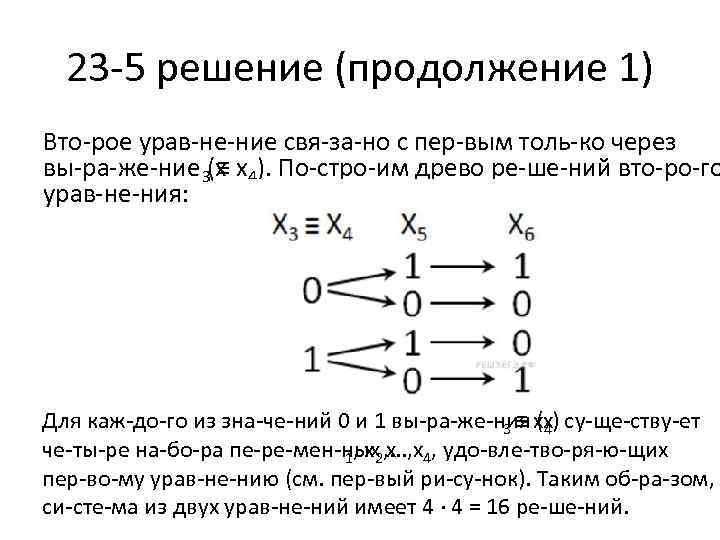23 5 решение (продолжение 1) Вто рое урав не ние свя за но с пер вым толь ко через вы ра же ние (x 4). По стро им древо ре ше ний вто ро го 3 ≡ x урав не ния: Для каж до го из зна че ний 0 и 1 вы ра же ния (x) су ще ству ет 3 ≡ x 4 че ты ре на бо ра пе ре мен ных x 4, удо вле тво ря ю щих 1, x 2, . . . , x пер во му урав не нию (см. пер вый ри су нок). Таким об ра зом, си сте ма из двух урав не ний имеет 4 · 4 = 16 ре ше ний.

23 5 решение (продолжение 2) Тре тье урав не ние свя за но со вто рым толь ко через вы ра же ние (x 6). По стро им древо 5 ≡ x ре ше ний тре тье го урав не ния: Для каж до го из зна че ний 0 и 1 вы ра же ния (x) су ще ству ет 5 ≡ x 6 2 · 4 = 8 на бо ров пе ре мен ных x , . . . , x 6, удо вле тво ря ю щих 1, x 2 пер во му урав не нию (см. пер вый и вто рой ри су нок). Таким об ра зом, си сте ма из трёх урав не ний имеет 8 · 4 = 32 ре ше ния