ЗАДАЧИ сопромат Пример 1. Проверить прочность тяги

ЗАДАЧИ сопромат

Пример 1. Проверить прочность тяги ВС (рис. 1). Материал - сталь Ст3, допускаемое напряжение [ т] = 160 МПа. Решение. Продольную силу N, возникающую в произвольном поперечном сечении тяги, определяем, применяя метод сечения и рассматривая равновесие балки AD (рис. 2. б): MA = 0; F l - (N sin ) a =0, откуда N = F l/a sin ; подставляя числовые значения, получаем N = 40 2, 5 / (2, 0 sin 30°) = 100 к. Н.

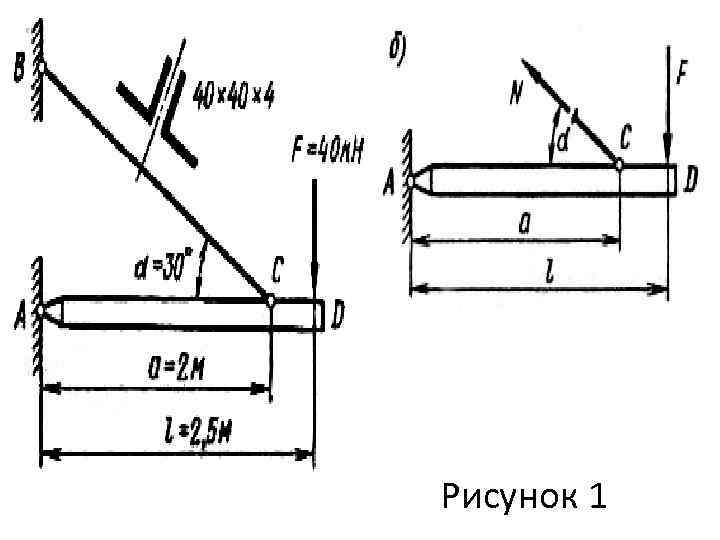Рисунок 1

Напряжения в поперечном сечении тяги где площадь поперечного сечения одного равнобокого уголка 40 х40 х4 А 1=3, 08 см 2 (по табл. ГОСТ 8509 -72). Площадь сечения тяги: А=2 А 1. Напряжение выше допускаемого всего на 1, 25%, следовательно, прочность тяги обеспечена.

Пример 2. Проверить прочность штифтового соединения вильчатого кривошипа с валом (рис. 2), если [ сp]=65 МПа и [ см]=90 МПа, F=2, 8 к. Н. Решение. Окружная сила, передаваемая штифтом, связана с силой F, приложенной к кривошипу, соотношением Ft = F h / (d/2) = 2, 8 180 / (0, 5 40) = 25, 2 к. Н. Напряжения среза, возникающие в продольном сечении штифта: сp = Ft / (d l) = 25, 2 103 / (0, 012 0, 05) = 42 106 Па = 42 МПа = 0, 645 [ сp].

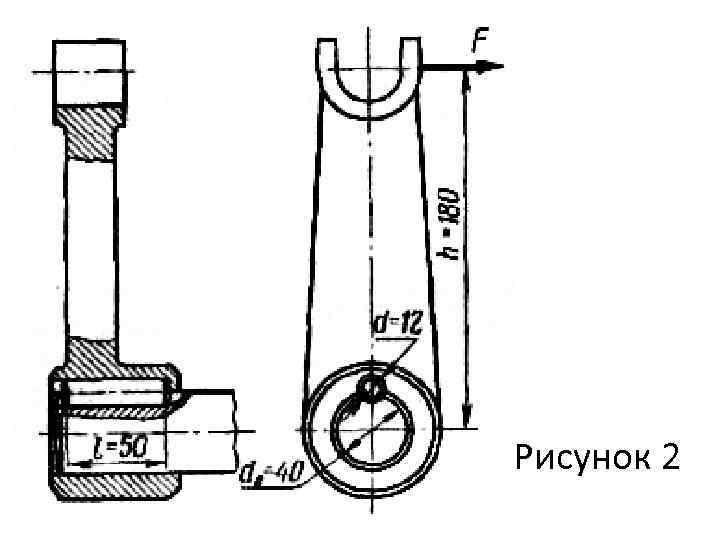Рисунок 2

При проверке соединения на смятие учтем, что поверхность контакта, через которую передается сила F 1, представляет собой четвертую часть поверхности цилиндра размерами d и l. Для поверхности полуцилиндра расчетная площадь смятия равна d l, следовательно, в данном случае Асм = 0, 5 d l; см= Ft /(0, 5 d l) = 25, 2 103/(0, 5 0, 012 0, 05) = 84 106 Па = 84 МПа = 0, 932 [ см].

Пример 3. Определить диаметр D и высоту h головки стержня, нагруженного растягивающей силой F (рис. 3). Расчет выполнить исходя из условия равнопрочности стержня на растяжение, головки на срез и ее опорной поверхности на смятие. Допускаемые напряжения: [ р]=140 МПа; [ ср]=100 МПа; [ см]=250 МПа. Решение. 1. Определяем допускаемую нагрузку из условия прочности стержня на растяжение:

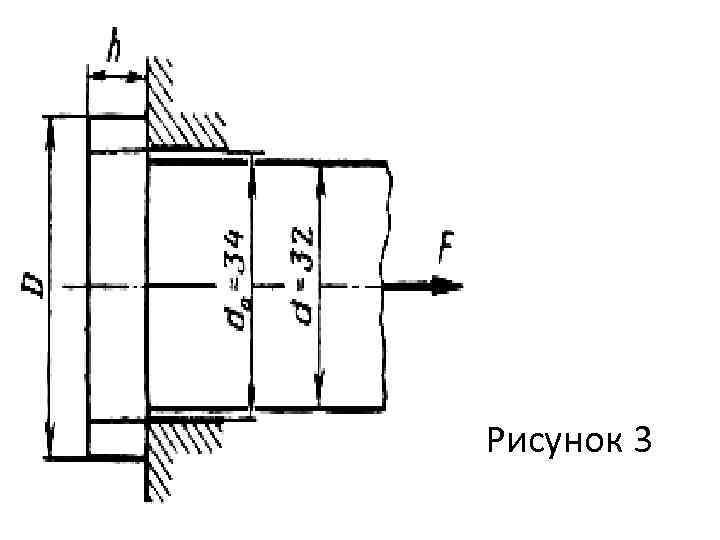Рисунок 3

3. Определяем высоту головки из условия прочности на срез: ср = F/Acp [ ср]. Площадь среза равна боковой поверхности цилиндра высотой h и диаметром dо (место возможного среза условно показано на рис. 3 волнистыми линиями). Принимая F = [Fp], получаем ср = F/ (π do h) [ ср]. Откуда Принимаем h = 11 мм.

Пример 4. Два одинаковых вала соединены муфтой со штифтами (рис. 4). Выяснить, что ограничивает передаваемый момент; прочность валов, муфты или штифтов. Принять для валов [ к]' = 40 МПа, для муфты [ к]" = 20 МПа, для штифтов [ ср] = 100 МПа. При расчете валов и муфт ослабление их отверстиями для штифтов не учитывать. Решение. 1. Допускаемый момент из условия прочности валов [М]B=[Мz]B=[ к]’ Wp. B=40 106 3, 14 0, 043/16=502 Н м.

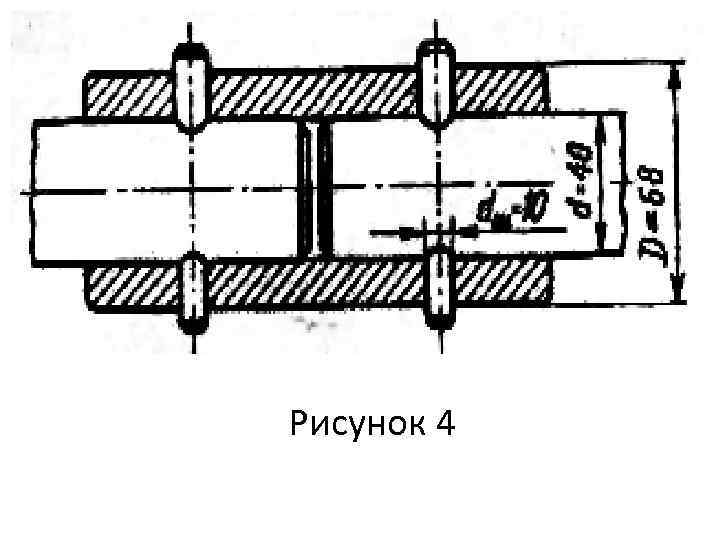Рисунок 4

2. Допускаемый момент из условия прочности муфты. 3. Допускаемый момент находим из условия прочности штифтов. Штифт работает на срез. Учитывая наличие двух плоскостей среза, получаем следующее расчетное уравнение: Сила, действующая на штифт, связана с передаваемым моментом зависимостью F = M/(0, 5 d).

Подставляя значение F в условие прочности, получаем. Откуда Таким образом, наименее прочными элементами конструкции являются штифты. Для увеличения допускаемого момента можно поставить на каждой половине муфты два штифта, одновременно несколько уменьшив их диаметр. Толщину втулки (муфты) можно несколько уменьшить, так как муфта значительно прочнее вала.

Пример 5. Стержень фермы, состоящий из двух швеллеров № 18 а, соединен с фасонным листом (косынкой) узла фермы заклепками расчетным диаметром d=17 мм (рис. 5). Определить требуемое число заклепок при допускаемых напряжениях: [ р]=160 МПа; [ cм] = 320 МПа; [ cp] = 140 МПа. Проверить прочность стержня. Решение. Допускаемая сила на одну заклепку из условия прочности на срез [Qcp] = [ cp] k πd 2/4 = 140 106 2 3, 14 0, 0172 /4 =63, 5 103 Н.

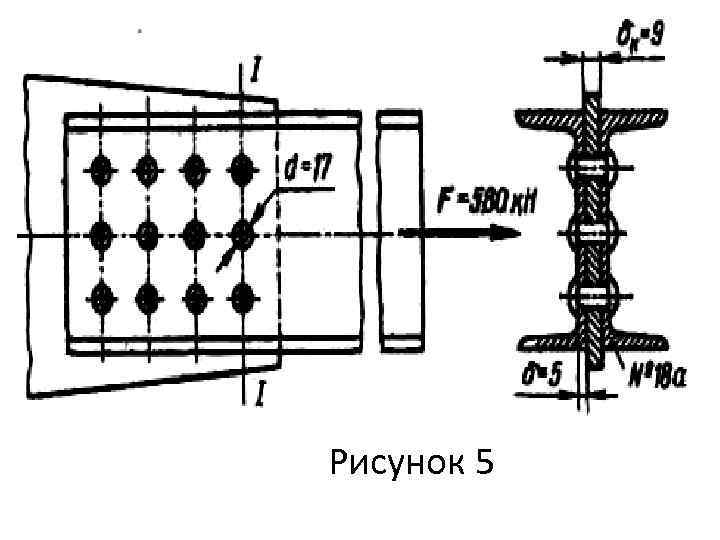Рисунок 5

Здесь принято k=2, т. е. заклепки двухсрезные. Допускаемая сила на одну заклепку из условия прочности на смятие [Qcм] = [ cм] d к = 320 106 0, 017 0, 009 = =49, 0 103 Н. Толщина косынки меньше удвоенной толщины стенки швеллера, поэтому она и принята в качестве расчетной. Требуемое число заклепок определяем из условия прочности на смятие, так как [Qcм] < [Qcр]: i F/[Qcм] = (580 103)/(49 103) 11, 8.

Принимаем i = 12. Напряжение в опасном сечении (I-I) стержня Здесь А=22, 2 см 2 – площадь сечения одного швеллера № 18 а.

Пример 6. Проверить прочность заданной стальной балки (рис. 6). Допускаемое напряжение [ ] = 120 МПа. Решение. Опорные реакции показаны на рис. 6, там же показана эпюра изгибающих моментов (предварительно надо построить). Опасное сечение С; наибольшее нормальное напряжение в этом сечении Это напряжение на 1 % выше допускаемого, что, конечно, не опасно, т. е. прочность балки обеспечена.

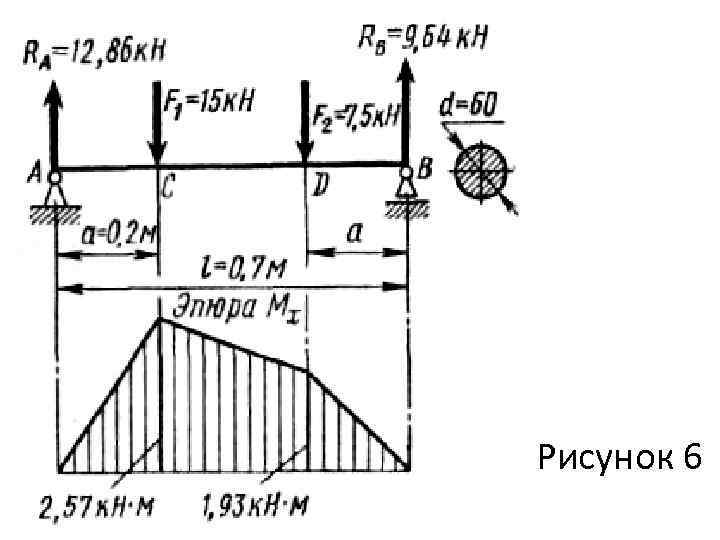Рисунок 6

Пример 7. Двутавровая балка (рис. 7, а) изготовлена из стали Ст3, имеющей предел текучести т=240 МПа. Проверить прочность балки, если заданный коэффициент запаса прочности [nт] = 1, 5. Решение. Определяем опорные реакции и строим эпюры Qy и Мх (рис. 7, б, в). Для расчета на прочность эпюра Q не нужна, но построение ее при действии на балку распределенной нагрузки целесообразно, так как по этой эпюре сразу определяется, имеет ли эпюра Мх точки экстремума и где именно. В нашем случае эпюра Qy имеет нулевую ординату в сечении, отстоящем на 2, 47 м от опоры А:

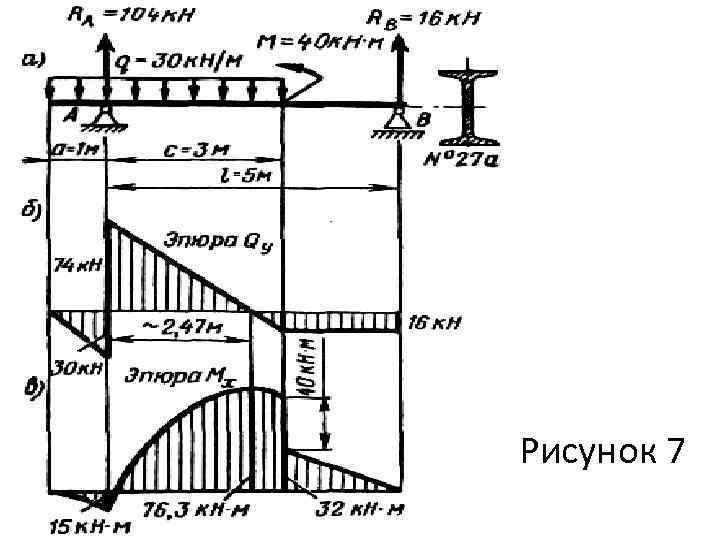Рисунок 7

MXmax=- 30 3, 47 (3, 47/2) + 104 2, 47 = 76, 3 к. Н м. Это расчетный момент. Необходимо подчеркнуть, что в некоторых случаях расчетное значение Мх может оказаться большим, чем соответствующее точке математического максимума. Наибольшее нормальное напряжение в опасном сечении max=MXmax/Wx = 76, 3 103/(407 10 -6) = 187, 5 106 Па =187, 5 МПа, где Wx = 407 см 3 - момент сопротивления (относительно нейтральной оси двутаврового профиля № 27 а по ГОСТ 8239 - 72).

Коэффициент запаса для опасных точек балки т. е. ниже требуемого на 14, 5%, следовательно, балка работает с весьма значительной перегрузкой.

Пример 8. Определить при [ ]=120 МПа допускаемую нагрузку для бруса круглого поперечного сечения (d = 80 мм), нагруженною, как показано на рис. 8, а. Решение. Определим результирующие изгибающие моменты и сечениях С и D использовав построенные на рис. 8, б, в эпюры Мх и Му :

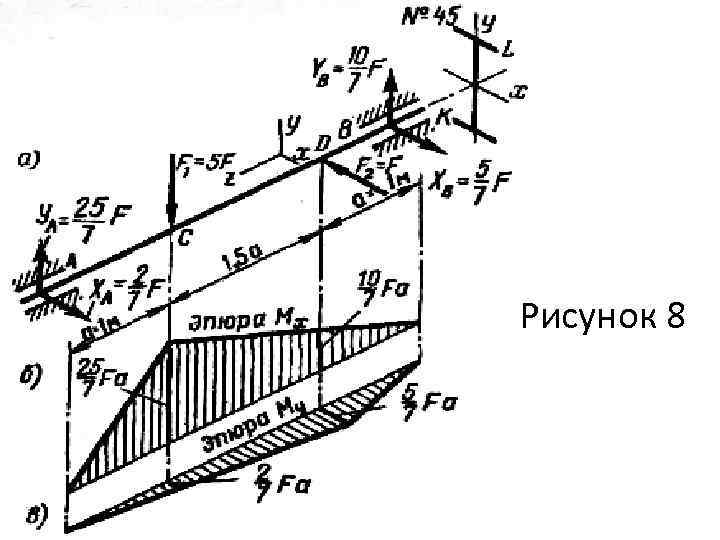Рисунок 8

Опасное сечение - С. Нетрудно убедиться, что ни в одном из сечений участка CD (а тем более участков АС и BD) результирующий момент не превышает значения Ми. С Условие прочности Откуда или

Интересно отметить, что при той же схеме нагружения, но иной форме поперечного сечения бруса опасным оказывается другое поперечное сечение - не то, где результирующий изгибающий момент максимален.

Пример 9 Проверить прочность винта домкрата (рис. 9) грузоподъемностью 100 к. Н, учитывая, что в поперечных сечениях нарезанной части винта помимо продольной силы возникает крутящий момент Mz=540 Н м. Внутренний диаметр резьбы d 1=48 мм. Расчет выполнить по третьей гипотезе прочности. Принять [ ] = 80 МПа. Решение. Нормальные напряжения в поперечном сечении винта (по абсолютной величине)

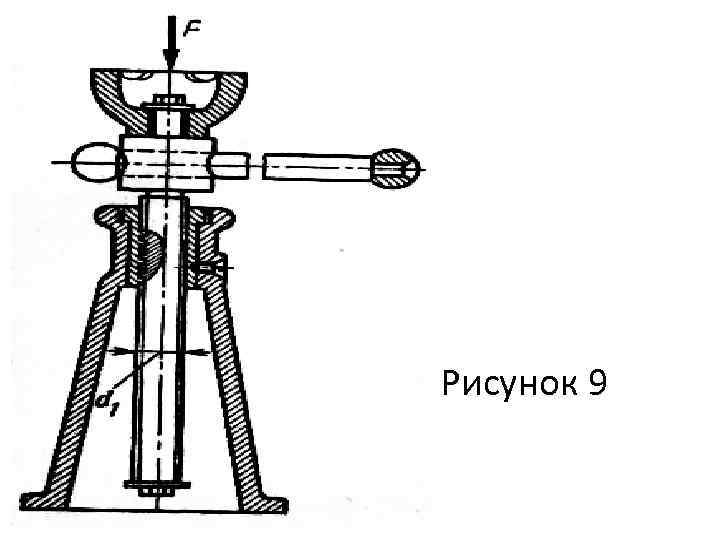Рисунок 9

Касательные напряжения в точках контура поперечного сечения Эквивалентное напряжение для опасной точки по гипотезе наибольших касательных напряжений что ниже допускаемого на 7%.

Пример 10. Проверить прочность бруса кольцевого поперечного сечения, нагруженного, как указано на рис. 10, а. Расчет вести по пятой гипотезе прочности, принимая [ ]=100 МПа. Решение. На рис. 10, б показаны эпюры внутренних силовых факторов (кроме Qy, влияние которой при расчете не учитывается). Определяем геометрические характеристики поперечного сечения бруса:

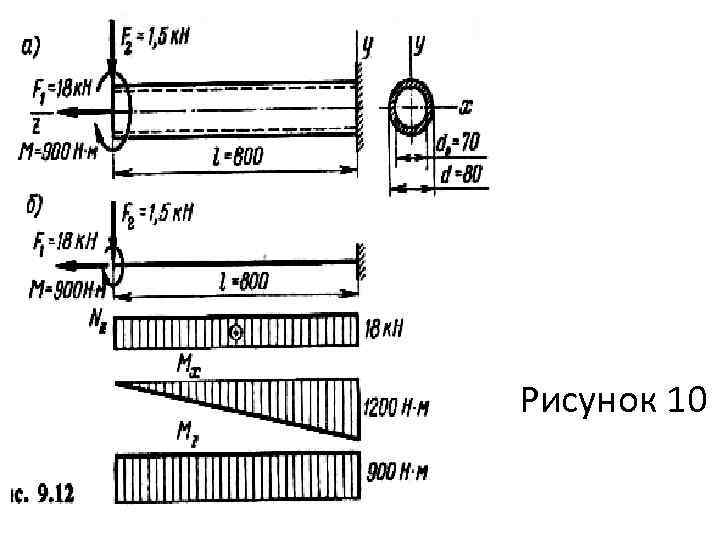Рисунок 10

Wи = 0, 5 Wp=0, 5 41, 6 103= 20, 8 103 мм 3=20, 8 10 -6 м 3. Вычисляем исходные напряжения в опасной точке опасного (в зацепке) поперечного сечения: `z= Nx =Nx/A=18 103/1180 10 -6=15, 25 106 Па =15, 25 МПа ``z= Mх мax = Nx/Wи=1200 103/(20, 8 10 -6)= 57, 7 106 Па = 57, 7 МПа z= `z+ ``z= 15, 25+57, 7 73 МПа z= Mz мax = Mz/Wp=900 103/(41, 6 10 -6)=21, 6 106 Па = 21, 6 МПа

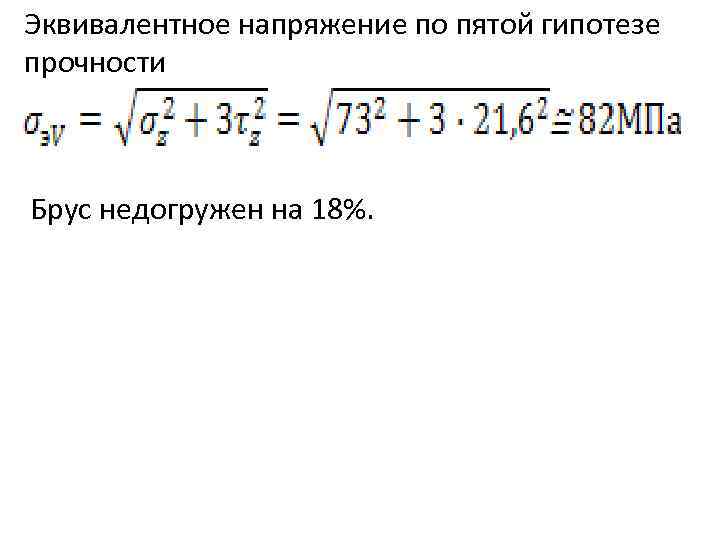Эквивалентное напряжение по пятой гипотезе прочности Брус недогружен на 18%.