Задачи на разрезание Все их сюжеты можно

Задачи на разрезание

Все их сюжеты можно условно поделить на следующие виды и подвиды: • на заданное число конгруэнтных и подобных ей фигур (такие фигуры получили название «делящихся» ); • определённым количеством прямых на максимально возможное число частей, не обязательно равных. • Трансформирование – требуется разрезать одну фигуру так, чтобы их её частей можно было сложить вторую заданную фигуру

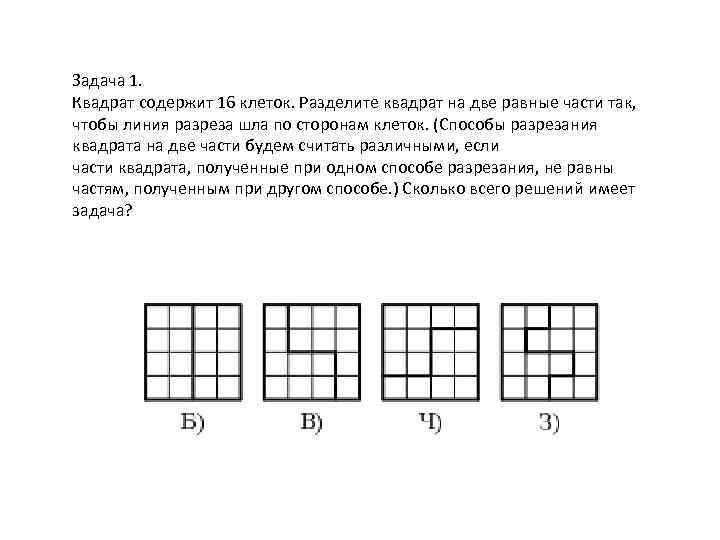Задача 1. Квадрат содержит 16 клеток. Разделите квадрат на две равные части так, чтобы линия разреза шла по сторонам клеток. (Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, не равны частям, полученным при другом способе. ) Сколько всего решений имеет задача?

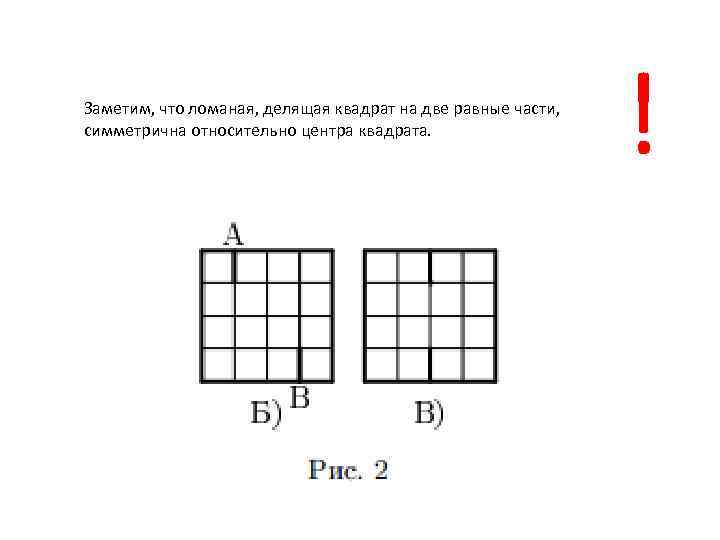Заметим, что ломаная, делящая квадрат на две равные части, симметрична относительно центра квадрата. !

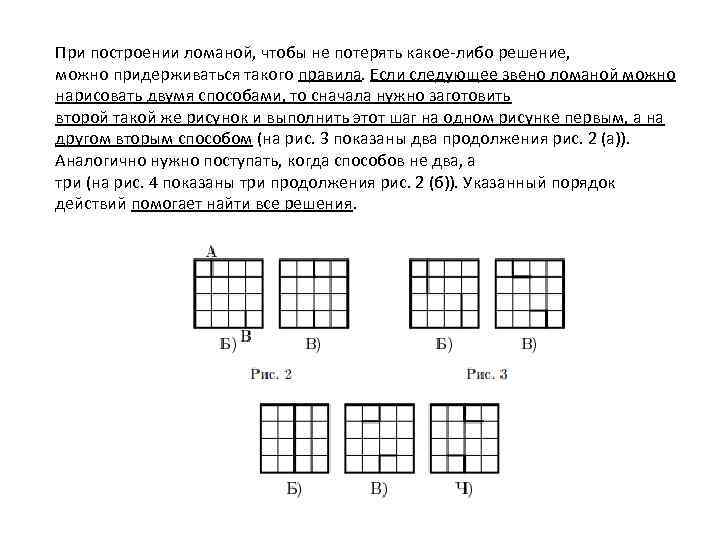При построении ломаной, чтобы не потерять какое-либо решение, можно придерживаться такого правила. Если следующее звено ломаной можно нарисовать двумя способами, то сначала нужно заготовить второй такой же рисунок и выполнить этот шаг на одном рисунке первым, а на другом вторым способом (на рис. 3 показаны два продолжения рис. 2 (а)). Аналогично нужно поступать, когда способов не два, а три (на рис. 4 показаны три продолжения рис. 2 (б)). Указанный порядок действий помогает найти все решения.

Задача 2 Прямоугольник 4 × 9 клеток разрежьте по сторонам клеток на две равные части так, чтобы из них затем можно было сложить квадрат.

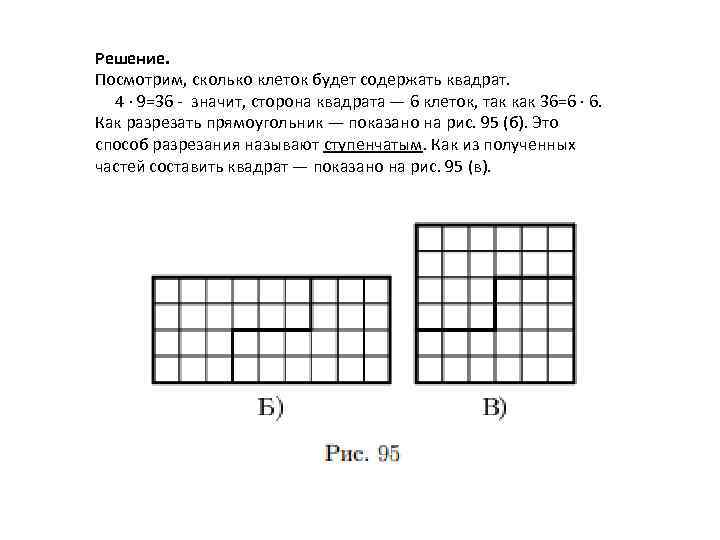Решение. Посмотрим, сколько клеток будет содержать квадрат. 4 · 9=36 - значит, сторона квадрата — 6 клеток, так как 36=6 · 6. Как разрезать прямоугольник — показано на рис. 95 (б). Это способ разрезания называют ступенчатым. Как из полученных частей составить квадрат — показано на рис. 95 (в).

Задача 3. Можно ли квадрат 5× 5 клеток разрезать на две равные части так, чтобы линия разреза шла по сторонам клеток? Ответ обоснуйте.

Решение. Нельзя, так квадрат состоит из 25 клеток. Его нужно разрезать на две равные части. Поэтому в каждой части должно быть по 12, 5 клеток, а значит, линия разреза будет проходить не по сторонам клеток.

Пентамино 12 фигур, каждая из которых состоит из пяти одинаковых квадратов, причем квадраты «соседствуют « друг с другом только сторонами. «ПЕНТА» - «ПЯТЬ» (с греческого)

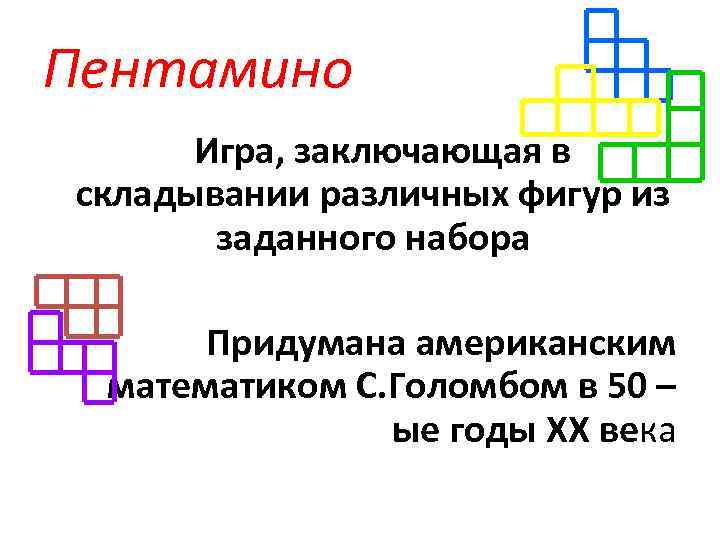Пентамино Игра, заключающая в складывании различных фигур из заданного набора Придумана американским математиком С. Голомбом в 50 – ые годы XX века

Задача Составьте все возможные фигуры пентамино.

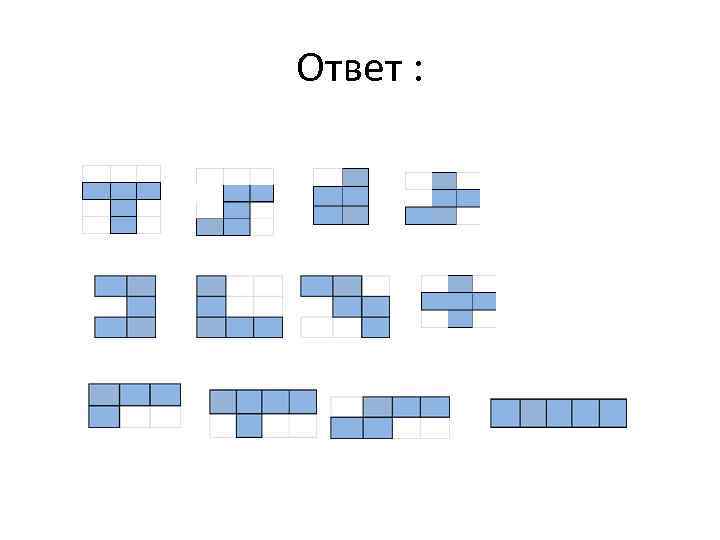Ответ :

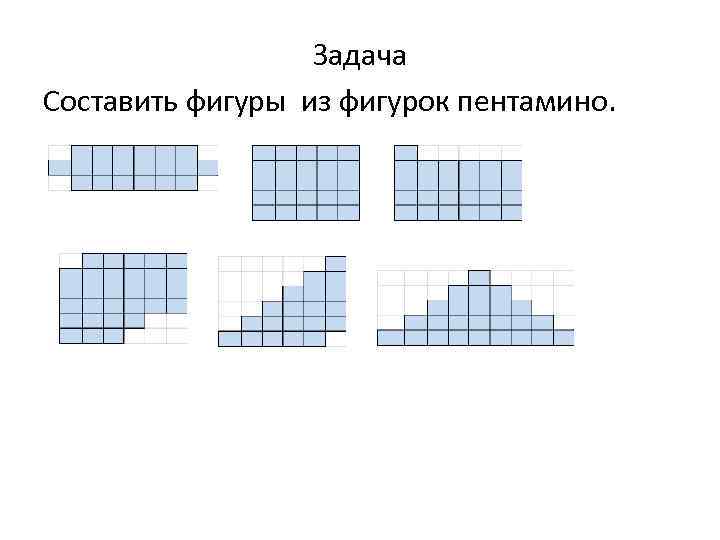Задача Составить фигуры из фигурок пентамино.

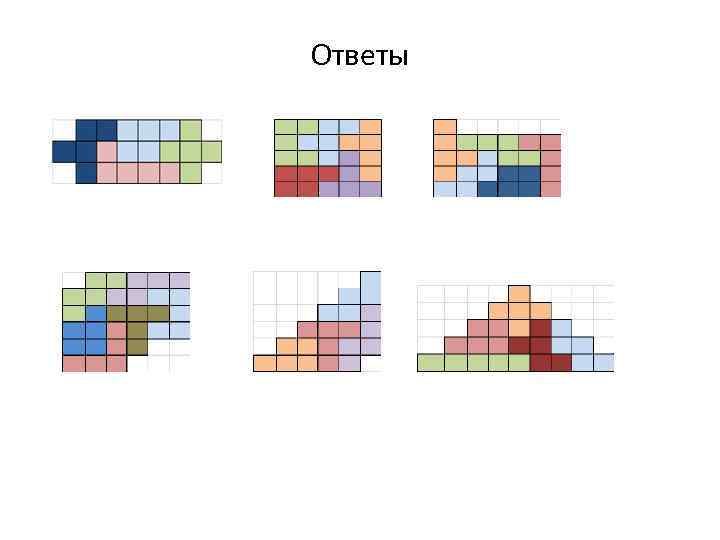Ответы

Разбиение плоскости

№ 1. Выложите плитками 2*1 пол в комнате размером 5*6 (сплошной паркет). Пусть у нас имеется неограниченный запас прямоугольных плиток размером 2*1, и мы хотим выложить ими пол прямоугольной формы, причем никакие две плитки не должны перекрываться.

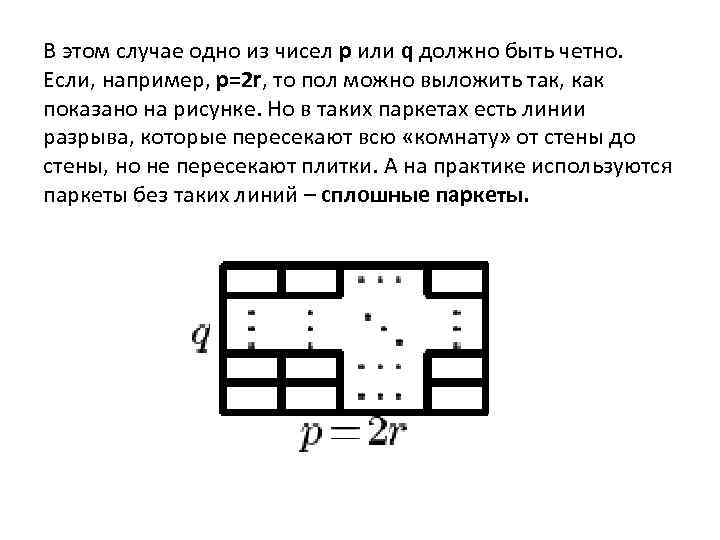В этом случае одно из чисел p или q должно быть четно. Если, например, p=2 r, то пол можно выложить так, как показано на рисунке. Но в таких паркетах есть линии разрыва, которые пересекают всю «комнату» от стены до стены, но не пересекают плитки. А на практике используются паркеты без таких линий – сплошные паркеты.

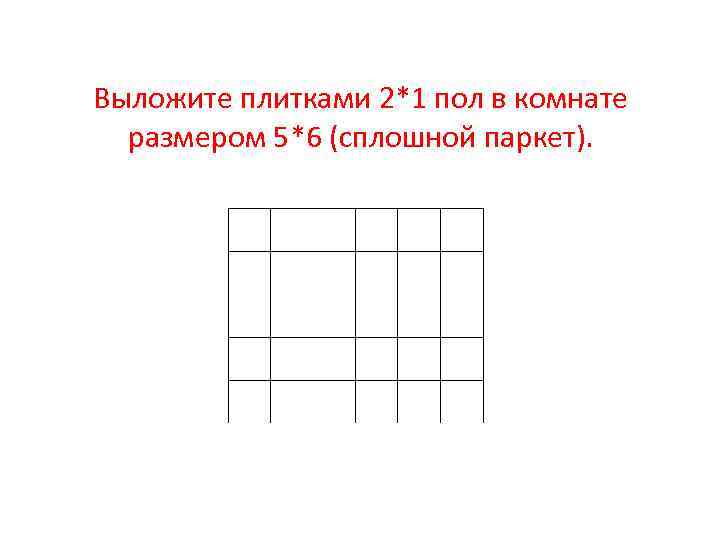Выложите плитками 2*1 пол в комнате размером 5*6 (сплошной паркет).

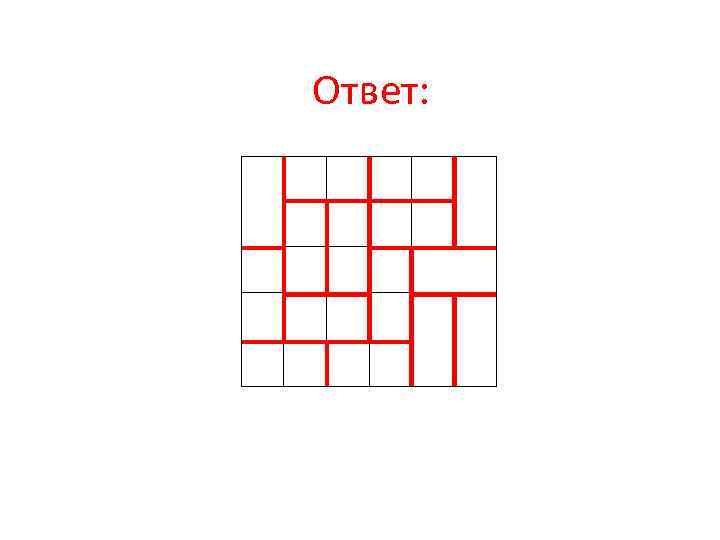Ответ:

Естественно возникает вопрос, при каких p и q прямоугольник p*q допускает сплошное разбиение на плитки 2*1? •

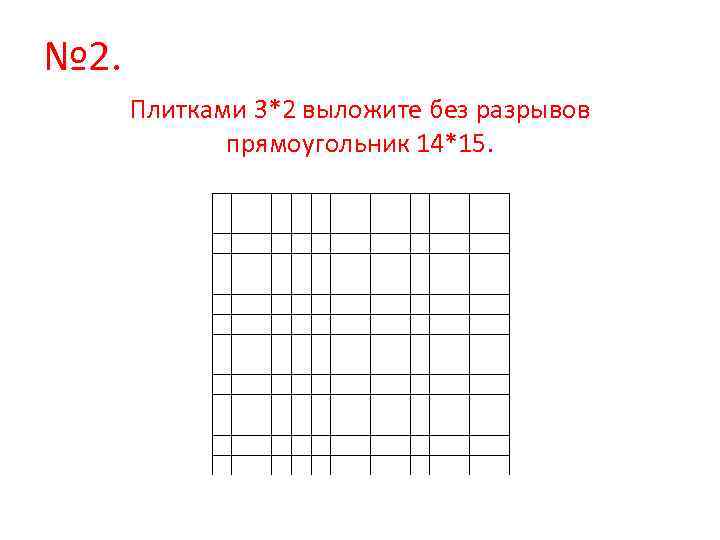№ 2. Плитками 3*2 выложите без разрывов прямоугольник 14*15.

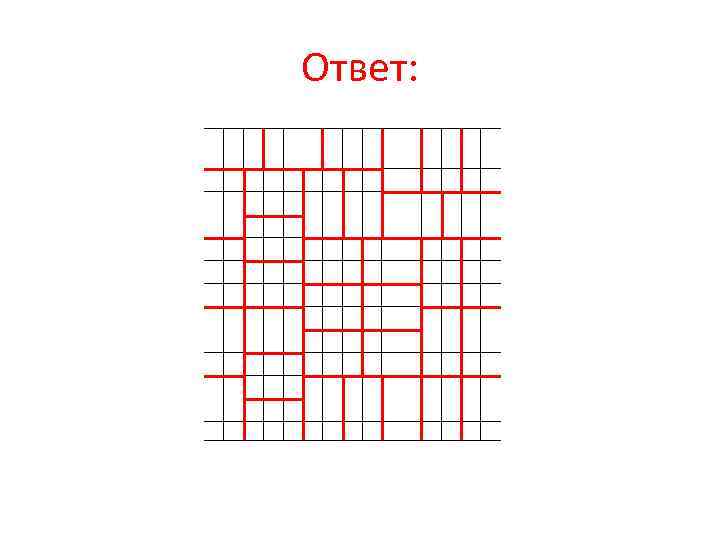Ответ:

№ 3. На листе клетчатой бумаги размерами 10*10 клеток наметьте разрезы, с помощью которых можно получить как можно больше целых фигур, изображенных на рисунке. Фигуры, изображенные на рисунке, можно переворачивать.

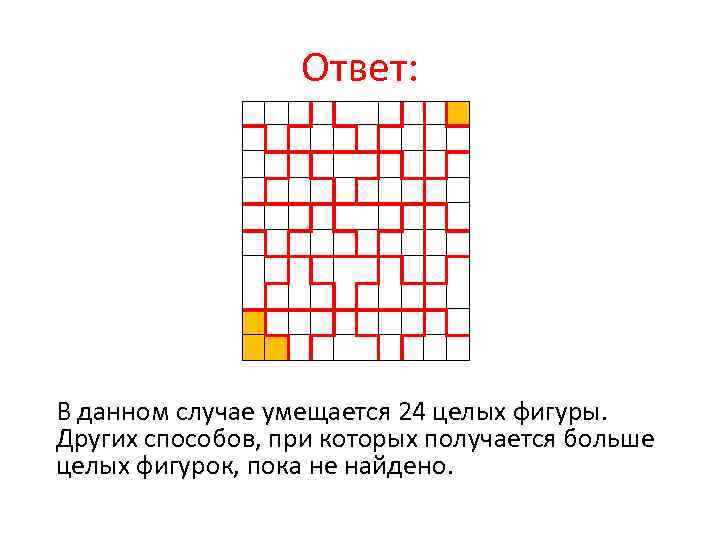Ответ: В данном случае умещается 24 целых фигуры. Других способов, при которых получается больше целых фигурок, пока не найдено.

Задача № 4

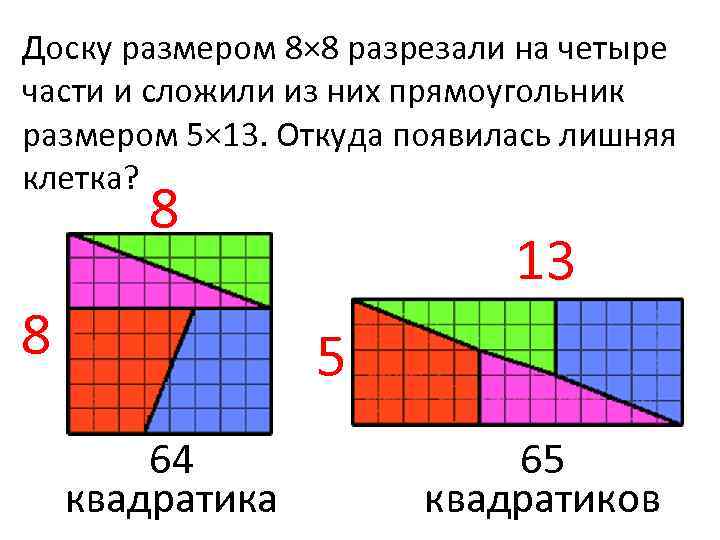Доску размером 8× 8 разрезали на четыре части и сложили из них прямоугольник размером 5× 13. Откуда появилась лишняя клетка? 8 8 13 5 64 квадратика 65 квадратиков

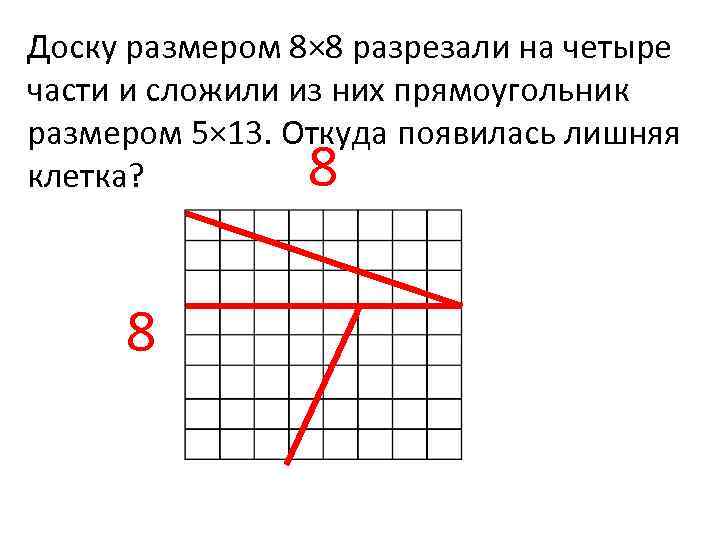Доску размером 8× 8 разрезали на четыре части и сложили из них прямоугольник размером 5× 13. Откуда появилась лишняя клетка? 8 8

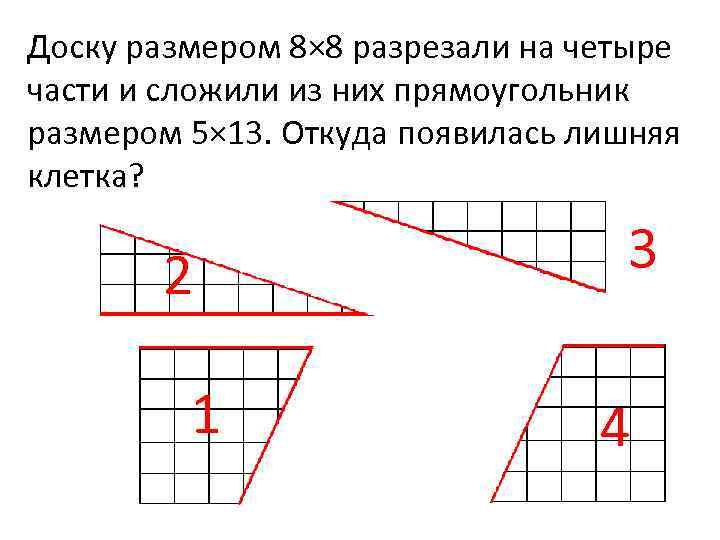Доску размером 8× 8 разрезали на четыре части и сложили из них прямоугольник размером 5× 13. Откуда появилась лишняя клетка? 2 1 3 4

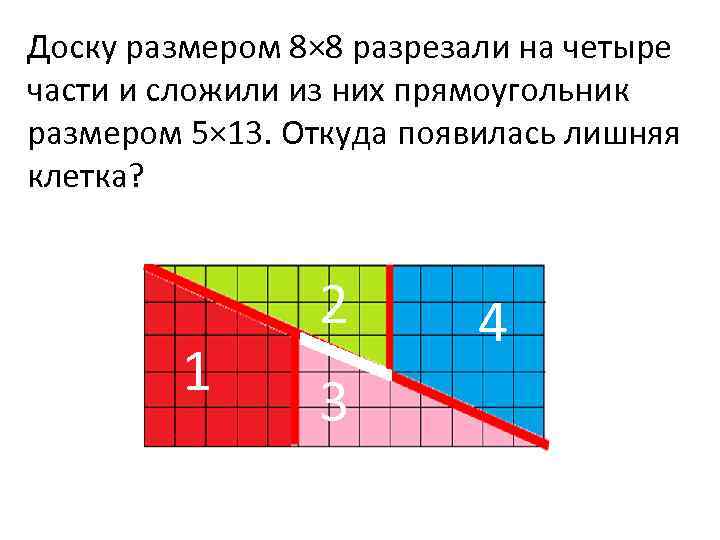Доску размером 8× 8 разрезали на четыре части и сложили из них прямоугольник размером 5× 13. Откуда появилась лишняя клетка? 1 2 3 4

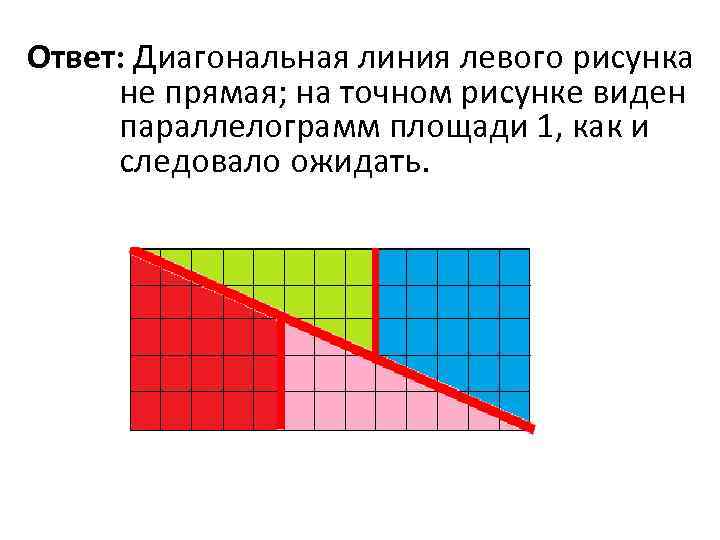Ответ: Диагональная линия левого рисунка не прямая; на точном рисунке виден параллелограмм площади 1, как и следовало ожидать.

Последовательность Фибоначчи j 1 = 1, j 2 = 1, j 3 = 2, j 4 = 3, j 5 = 5, j 6 = 8, j 7 = 13, j 8 = 21, j 9 = 34, j 10 = 55, j 11 = 89, . . . обладает следующим свойством: квадрат числа Фибоначчи на 1 отличается от произведения предшествующего ему и следующего за ним чисел Фибоначчи; точнее говоря, jn 2 + (– 1)n = jn – 1 jn + 1.

Например, при n = 6 формула превращается в равенство 82 + 1 = 5 · 13, а при n = 7 — в равенство 132 – 1 = 8 · 21. Советую нарисовать картинки, аналогичные рисунку к условию задачи, для нескольких других значений n.