Задачи на концентрацию и процентное содержание

«Задачи на концентрацию и процентное содержание»

В наше время почти во всех областях человеческой деятельности встречаются проценты. Поэтому выбранная мной тема особенно актуальна. Без понятия «процент» нельзя обойтись ни в бухгалтерском учёте, ни в финансовом анализе, ни в статистике. Чтобы начислить зарплату работнику, нужно знать процент налоговых отчислений; чтобы открыть депозитный счёт в сбербанке, наши родители интересуются размером процентных начислений на сумму вклада; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции. Именно в торговле понятие «процент» используется наиболее часто: скидки, наценки, уценки, прибыль, кредиты, налог на прибыль и т. д. – всё это проценты. Цель данной урока - показать широту применения процентов и исследовать их использование в металлургической и химической промышленности. Для достижения поставленной цели необходимо выполнить следующие задачи: - проанализировать литературу по теме «Проценты и процентные вычисления» ; - изучить «Закон сохранения объёма и массы» ; - показать прием полученных знаний при решении задач. Решение математических задач практического содержания позволяет убедиться в значении математики для различных сфер человеческой деятельности, увидеть широту возможных приложений математики, понять её роль в современной жизни. Умение выполнять процентные расчеты необходимо каждому человеку. Поэтому сюжеты задач взяты из реальной жизни. Ценность полученных результатов в том, что они продемонстрировали широкий спектр применения расчёта процентов в экономических сферах, то есть тесную взаимосвязь математики с экономикой.

Рационально мыслить и рационально считать – таков девиз при решении задач. История возникновения процента. Слово «процент» имеет латинское происхождение: «pro centum» - это «на сто» . Часто вместо слова «процент» используют это словосочетание. То есть процентом называется сотая часть числа. Проценты были известны индийцам ещё в V в. и это очевидно, так как именно в Индии с давних пор счет велся в десятичной системе счисления. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Римляне брали с должника лихву (т. е. деньги сверх того, что дали в долг). При этом говорили: «на каждые 100 сестерциев долга заплатить 16 сестерциев лихвы» . Это можно назвать первым кредитом мира. От римлян проценты перешли к другим народам Европы. В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. В 1584 г. Он впервые опубликовал таблицу процентов. Введение процентов было удобным для определения содержания одного вещества в другом; в процентах стали измерять количественное изменение производства товара, рост и спад цен, рост денежного дохода и т. д. Символ появился не сразу. Сначала писали слово «сто» так: сtо. В 1685 г. в Париже была напечатана книга «Руководство по коммерческой арифметике» , где по ошибке вместо сtо было набрано . После этого знак получил всеобщее признание и до сих пор мы пользуемся этим значком процента.

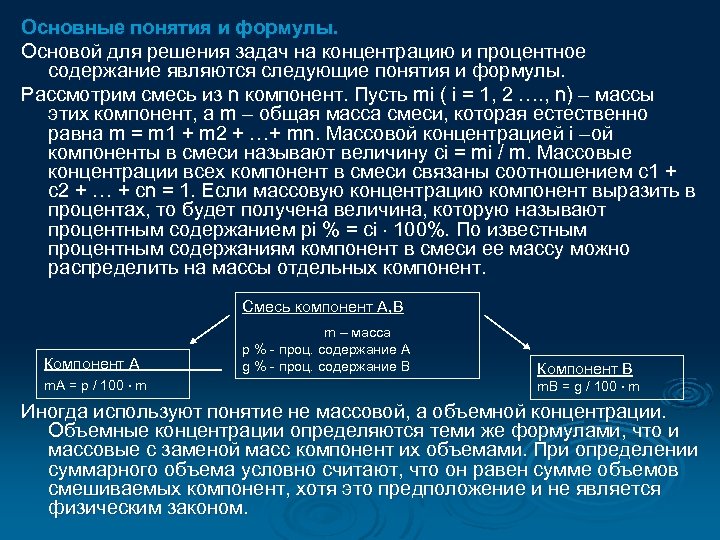Основные понятия и формулы. Основой для решения задач на концентрацию и процентное содержание являются следующие понятия и формулы. Рассмотрим смесь из n компонент. Пусть mi ( i = 1, 2 …. , n) – массы этих компонент, а m – общая масса смеси, которая естественно равна m = m 1 + m 2 + …+ mn. Массовой концентрацией i –ой компоненты в смеси называют величину ci = mi / m. Массовые концентрации всех компонент в смеси связаны соотношением c 1 + c 2 + … + cn = 1. Если массовую концентрацию компонент выразить в процентах, то будет получена величина, которую называют процентным содержанием pi % = ci 100%. По известным процентным содержаниям компонент в смеси ее массу можно распределить на массы отдельных компонент. Смесь компонент A, B Компонент А m. A = p / 100 m m – масса p % - проц. содержание А g % - проц. содержание В Компонент В m. B = g / 100 m Иногда используют понятие не массовой, а объемной концентрации. Объемные концентрации определяются теми же формулами, что и массовые с заменой масс компонент их объемами. При определении суммарного объема условно считают, что он равен сумме объемов смешиваемых компонент, хотя это предположение и не является физическим законом.

Одним из наиболее распространенных типов задач на концентрацию являются задачи, в которых из нескольких смесей с заданным содержанием составляется новая смесь из каких-то частей исходных смесей. Рассмотрим подобные примеры.

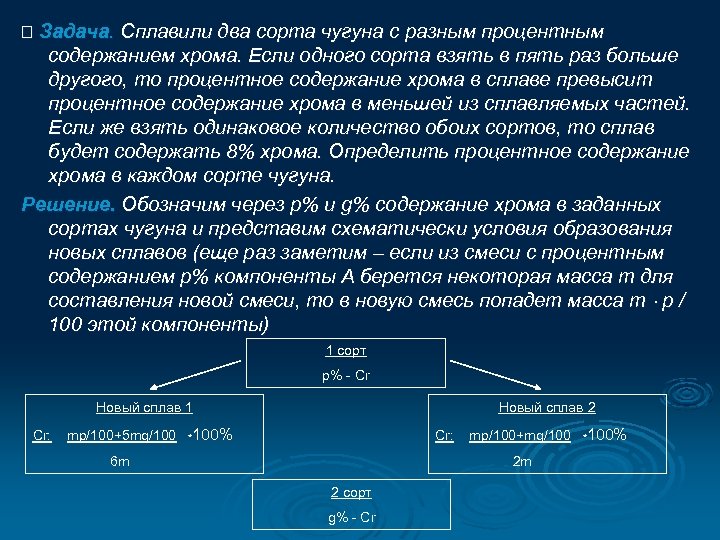Задача. Сплавили два сорта чугуна с разным процентным содержанием хрома. Если одного сорта взять в пять раз больше другого, то процентное содержание хрома в сплаве превысит процентное содержание хрома в меньшей из сплавляемых частей. Если же взять одинаковое количество обоих сортов, то сплав будет содержать 8% хрома. Определить процентное содержание хрома в каждом сорте чугуна. Решение. Обозначим через р% и g% содержание хрома в заданных сортах чугуна и представим схематически условия образования новых сплавов (еще раз заметим – если из смеси с процентным содержанием р% компоненты А берется некоторая масса т для составления новой смеси, то в новую смесь попадет масса т р / 100 этой компоненты) 1 сорт р% - Cr Новый сплав 1 Cr: mp/100+5 mg/100 Новый сплав 2 *100% Cr: 6 m mp/100+mg/100 2 m 2 сорт g% - Cr *100%

Используя данные рисунка и условия задачи, получаем систему p + 5 g = 2 p 6 p+g=8 2 откуда р=5%, g=11% Ответ: р=5%, g=11%. или 5 g = 11 p p + g = 16

Особенность следующей задачи в том, что задаётся не процентное содержание компонент, а пропорция, определяющая их соотношение в смеси. Например, пусть компоненты А и В находятся в смеси в отношении А: В = r: s, то в некоторой массе m такой смеси массы компонент составит m=r/(r+s) и m=s/(r+s)

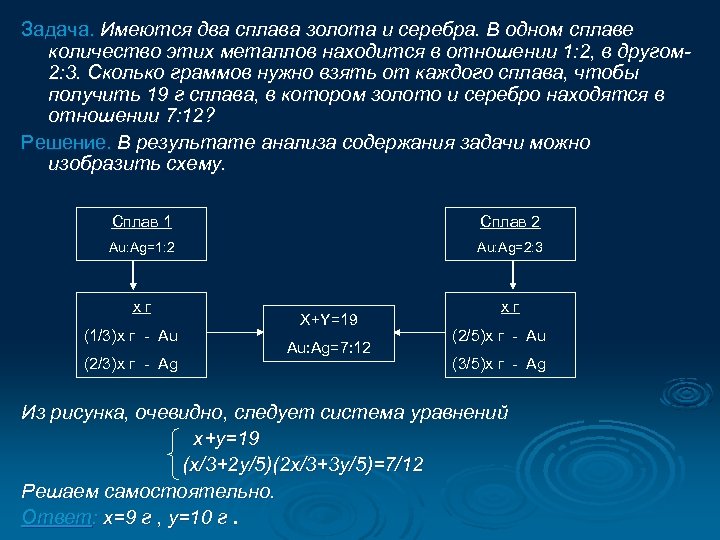Задача. Имеются два сплава золота и серебра. В одном сплаве количество этих металлов находится в отношении 1: 2, в другом 2: 3. Сколько граммов нужно взять от каждого сплава, чтобы получить 19 г сплава, в котором золото и серебро находятся в отношении 7: 12? Решение. В результате анализа содержания задачи можно изобразить схему. Сплав 1 Сплав 2 Au: Ag=1: 2 Au: Ag=2: 3 xг xг (1/3)x г - Au (2/3)x г - Ag X+Y=19 Au: Ag=7: 12 (2/5)x г - Au (3/5)x г - Ag Из рисунка, очевидно, следует система уравнений x+y=19 (x/3+2 y/5)(2 x/3+3 y/5)=7/12 Решаем самостоятельно. Ответ: x=9 г , y=10 г.

В следующем примере состав смеси будет определяться через объёмные концентрации.

Задача. Три одинаковые пробирки наполнены до половины растворами спирта. После того как содержимое третьей пробирки разлили поровну в первые две , объёмная концентрация в первой уменьшилась на 20% от первоначальной, а во второй увеличилась на 10% от первоначального значения. Во сколько раз первоначальное количество спирта в первой пробирке превышало первоначальное количество спирта во второй пробирке? Решение. Пусть объём каждой пробирки V=1, а объемные концентрации спирта в каждой из них C 1, С 2, С 3. С учетом того, что пробирки наполнены до половины, найдём исходные объёмы спирта в каждой из них V 1=c 1; V/2=c 1/2; V 2=c 2/2; V 3=c 3/2. После того, как содержимое третьей пробирки разлили поровну в первые две и, следовательно, растворы спирта заполнили их на ¾ , объёмы спирта в этих пробирках стали равны V 1*=c 1/2+c 3/4; V 2*=c 2/2+c 3/4. Чтобы определить новые объёмные концентрации надо разделить V 1* и V 2* на 3/4 V=3/4 1. В результате получим c 1 =1/3(2 c 1+c 3), c 2 =1/3(2 c 2+c 3). Объёмная концентрация спирта в первой пробирке уменьшилась на 20% от первоначальной и составила 0, 8 c 1, а во второй увеличилась на 10% от первоначальной и стала равной 1, 1 c 2. Таким образом, имеем систему (2 c 1+c 3)/3=0, 8 c 1 (2 c 2+c 3)/3=1, 1 с2 после преобразования которой получим 2 c 1 -5 c 3=0 с1/c 3=5/2 13 c 2 -10 c 3=0 или c 2/c 3=10/13 откуда c 1/c 2=13/4. Ответ: в 13/4 раза.

Задача. Имеются два сосуда с раствором поваренной соли: в первом сосуде - 3 кг 10%-ного раствора, а во втором - 2 кг 8%-ного раствора. Из первого сосуда выпаривают некоторое количество воды, а затем всё содержимое второго сосуда переливают в первый. Какое количество воды нужно выпарить, чтобы после переливания в первом сосуде получился r%-ный раствор? Найти все r, при которых задача имеет решение. Решение. m(масса) % содержание 1 сосуд 3 кг 10% 2 сосуд 2 кг 8% Пусть x – количество воды, выпаренной из первого раствора. Тогда после выпаривания в первом растворе останется 0, 9 3 – x = 2, 7 - x кг воды и 0, 1 3 = 0, 3 кг воды Так как во втором растворе содержится 0, 92 2 = 1, 84 кг воды и 0, 08 2 = 0, 16 кг соли, то после смешивания мы получим раствор, содержащий 2, 7 - x + 1, 84 = 4, 54 - x кг воды и 0, 3 + 0, 16 = 0, 46 кг соли. Согласно условию задачи имеем уравнение: (0, 46 100%)/(4, 54 - x + 0, 46)=r % (5 r – 46)=r Так как 0 ≤ x ≥ 2, 7, получаем следующее неравенство: 0 ≤ 5 r – 46/r ≤ 2, 7 9, 2 ≤ r ≤ 20 Ответ: (5 r – 46)/r; 9, 2 ≤ r ≤ 20.

Задача. Имеется три сплава. Первый сплав содержит 30% никеля и 70% меди, второй – 10% меди и 90% марганца, третий – 15% никеля, 25% меди и 60% марганца. Из них необходимо приготовить новый сплав, содержащий 40% марганца. Какое наименьшее и какое наибольшее количество меди может быть в этом новом сплаве? Решение. Никель Медь Марганец 1 сплав 30% 70% 2 сплав 10% 90% 3 сплав 15% 25% 60% Нов. Сплав 40% Пусть x, y, z процентное содержание соответственно первого, второго и третьего сплавов в новом сплаве. Тогда согласно условиям задачи, 0, 3 + 0, 15 z; 0, 9 y + 0, 6 z и 0, 7 x + 0, 1 y + 0, 25 z процентное содержание соответственно никеля, марганца и меди в новом сплаве. Значит, условие задачи можно сформулировать следующим образом: “Какое наименьшее и какое наибольшее значение может принимать выражение 0, 7 x + 0, 1 y + 0, 25 z при условии, что 0, 9 y + 0, 6 z = 40 и x + y + z =100? ”

Пусть 0, 7 x + 0, 1 y + 0, 25 z = t, тогда 14 x = 20 t – 2 y – 5 z. Имеем: 0, 9 y + 0, 6 z = 40 27 y + 18 z = 1200 x + y + z = 100 18 z = 2800 – 24 y – 40 t 14 x = 20 t – 2 y – 5 z 9 y + 6 z = 400 40 t = 1600 + 3 y 14 x + 14 y + 14 z = 1400 9 y +6 z = 400 14 x = 20 t – 2 y – 5 z 9 y + 6 z = 400 20 t + 12 y + 9 z = 1400 14 x = 20 t – 2 y – 5 z Из первого уравнения системы следует, что возможное наименьшее значение t достигается при y= 0 и равно t=40. При этом z =200/3, а x =100/3. С другой стороны, t максимально, когда максимально y. Но из второго уравнения системы вытекает, что y принимает наибольшее значение при z= 0, тогда y=400/9. При этом 130/3 и x = 500/9. Ответ: 40% и 130/3%.

Задача. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1, 5%? Решение. m воды соль m соли 30 кг 5% 30/100 5 x + 30 кг 1, 5% 30 + x/100 1, 5 Получим уравнение 30 + x/100 1, 5 = 30/100 5 45 + 1, 5 x = 150 1, 5 x = 105 x = 70 (кг) Ответ: 70 кг.

Задача. Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди? Решение. 1 сплав m ─ 36 кг pм. ─ 45% 2 сплав m ─ x кг gц. % ─ 60% Медь Цинк 1 сплав 45% 55% 2 сплав 60% 40% Решение. 1) 36 0, 45 = 16, 2 (кг) меди 2) 36 – 16, 2 = 19, 8 (кг) цинка Получим уравнение 36/100 55 = 36 + x/100 40 40 x = 540 x =13, 5 кг Ответ: 13, 5 кг.

Задача. Сплав меди с серебром содержит серебра на 1845 г больше, чем меди. Если бы к нему добавить некоторое количество чистого серебра, по массе равное ⅓ массы чистого серебра, первоначально содержащегося в сплаве, то получился бы новый сплав, содержащие 83, 5% серебра. Какова масса сплава и каково первоначальное процентное содержание в нем серебра? Решение. Медь Серебро 1 сплав xг x + 1845 г 100 – y% 2 сплав xг x+1845+ ⅓(x + 1845)=4/3(x+1845) 16, 5% 83, 5% Получим уравнение (x +4/3(x + 1845))/(100 16, 5)=x (7 x/3 + 4 1845/3) 16, 5 = 100 x (7 x + 4 1845) 5, 5 = 100 x 38, 5 x = 4 1845 5, 5 = 100 x 61, 5 x = 4 1845 5, 5 615 x = 4 1845 55 x = 660 (г) меди 660 + 1845 = 2505(г) серебра 2505 + 660 = 3165 (г) масса сплава 2505/3165 100 79% первоначальное % содержание серебра Ответ: 3165 г; 79%.

Задача. Найти процентное содержание олова в сплаве, полученном из двух кусков массой m 1 и m 2, если известно, что первый содержит p 1 %, а второй – p 2 % олова. Решение. Масса олова до сплавления: m 1(p 1/100)+m 2(p 2/100) Масса олова после сплавления: (m 1+m 2)(p/100) Так как они равны, то выполняется равенство: m 1(p 1/100)+m 2(p 2/100)=(m 1+m 2)(p/100) или m 1 p 1+m 2 p 2=(m 1+m 2)p Получаем: p=(m 1 p 1+m 2 p 2)/(m 1+m 2) Ответ: p=(m 1 p 1+m 2 p 2)/(m 1+m 2).

Задача. Имеются два слитка золота с серебром. Процентное содержание золота в первом слитке в 2, 5 раза больше, чем процентное содержание золота во втором слитке. Если сплавить оба слитка вместе, то получится слиток, в котором будет 40% золота. Найдите, во сколько раз первый слиток тяжелее второго, если известно, что при сплаве равных по весу частей первого и второго слитков получается сплав, в котором 35% золота. Решение. Масса золота Масса слитков Концентрация 1 -й слиток xy x y% 2 -й слиток 0, 4 xyk kx 0, 4 y%=(y/2, 5)% Первый сплав xy+0, 4 xy kx+kx 40%=(xy+0, 4 xyk)/(x+kx) 1 -й слиток m y my% 2 -й слиток 0, 4 my m 0, 4 y%=(y/2, 5)% Второй сплав my+0, 4 my 2 m 35%=(my+0, 4 my)/(2 m)

Составим и решим систему уравнений: (xy+0, 4 xyk)/(x+kx)=40 y+0, 4 yk=40+40 k 1, 4 y=70 (my+0, 4 my)/(2 m)=35 m≠ 0, k≠ 1, x≠ 0 y=50 50+0, 4 • 50 k=40+40 k 10=20 k k=1/2 Итак, 1 -й слиток в два раза тяжелее 2 -го. Ответ: в два раза.