Задачи математической статистики 1 -ая задача математической статистики-

Задачи математической статистики 1 -ая задача математической статистики- указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально проведенных экспериментов. 2 -ая задача - разработать методы анализа статистических данных в зависимости от целей исследования. 1

Основные понятия математической статистики Генеральной совокупностью называется множество числовых значений рассматриваемой количественной характеристики всех исследуемых объектов. Выборочной совокупностью (или просто выборкой) называется множество числовых значений рассматриваемой количественной характеристики для объектов, случайным образом отобранных из всей совокупности рассматриваемых объектов. Объемов совокупности (выборочной или генеральной) называют число объектов этой совокупности. 2

Основные определения Ряд наблюдений, упорядоченный по возрастанию, называется вариационным рядом. Различные значения признака, появившиеся в процессе наблюдения, называют вариантами. Число ni, показывающее сколько раз появилось значение xi в n наблюдениях, называют частотой данного значения, а отношение wi=ni/n – относительной частотой. Число k различных значений в n наблюдениях всегда конечно и k ≤ n. Имеют место равенства: 3

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Пример1. 4

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Оценки параметров генеральной совокупности, полученные на основании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, то она называется точечной. Если статистическая оценка характеризуется двумя числами – концами интервала, то она называется интервальной. К числу точеных оценок относятся выборочная средняя и выборочная дисперсия. 5

Статистические оценки должны отвечать определенным требованиям, чтобы соответствовать оцениваемым параметрам , т. е. иметь близкие к ним значения. Эти требования: несмещенность – математическое ожидание оценки должно равняться оцениваемому параметру т. е. эффективность- оценка при заданном объеме выборки должна обеспечивать наименьшую дисперсию т. е. состоятельность – по мере увеличения объема выборки оценка должна сходиться по вероятности к оцениваемому параметру т. е 6

Достоверной вероятностью (надежностью) оценки параметра называется вероятность β, с которой осуществляется неравенство , где δ положительной число, характеризующее точность оценки. В качестве величины β принимают число близкое к единице ( обычно β имеет значения 0, 90; 0, 95; 0, 99). Соотношение определяет вероятность того, что неизвестный параметр с доверительной вероятностью β находится в пределах доверительного интервала. 7

Точечные оценки. Выборочная средняя. Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось n 1 раз x 2 - n 2 раз xk- nk раз и - объем выборки. Выборочная средняя определяется как среднее арифметическое полученных по выборке значений. , где xi – варианта выборки; ni – частота варианты; n- объем выборки. 8

Точечные оценки. Выборочная дисперсия представляет собой среднюю арифметическую квадратов отклонений вариант от их выборочной средней. Удобно использовать формулу: где - выборочная средняя квадратов вариант выборки. Выборочная средняя является оценкой математического ожидания случайной величины и представляет собой несмещенную оценку. Выборочная дисперсия оценивает дисперсию генеральной совокупности, является смещенной оценкой. Для устранения смещения вычисляют. s 2 называют несмещенной выборочной дисперсией. 9

Статистическая проверка статистических гипотез Статистической называют гипотезу о виде неизвестного распределения или о параметра х известных распределений. Гипотеза о том, что две совокупности , сравниваемые по одному или нескольким параметрам не отличаются считается нулевой гипотезой. Нулевой гипотезой (основной)называют выдвинутую гипотезу Н 0. Конкурирующей (альтернативной) называют гипотезу Н 1, которая противоречит нулевой. Поскольку проверку проводят статистическими методами, то её называют статистической. 10

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода равна уровню значимости. Ошибка второго рода - гипотеза Н 0 принимается, а на самом деле она неверна. Вероятность ошибки второго рода равна β. Соответственно тогда вероятность принять верную гипотезу равна . вероятность отвергнуть неверную гипотезу равна 1 - β называется мощностью критерия. 11

Алгоритм проверки статистической гипотезы 1. Для проверки нулевой гипотезы по данным выборки вычисляют частные значения величин, входящих в критерий, и таким образом получают частное (наблюденное) значение критерия. К набл. 2. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия при котором нулевая гипотеза отвергается, а другая – при котором она принимается. В зависимости от принятого уровня значимости из области допустимых значений функции критерия К выделяют критическую область. 3. Далее используют следующее правило: если вычисленное по выборке значение критерия Кнабл попадает в критическую область, то гипотеза Н 0 отвергается и принимается гипотеза Н 1. При этом возможно, что гипотеза Н 0 справедлива, и следовательно, совершение ошибки первого рода есть вероятность ( величина ). 12

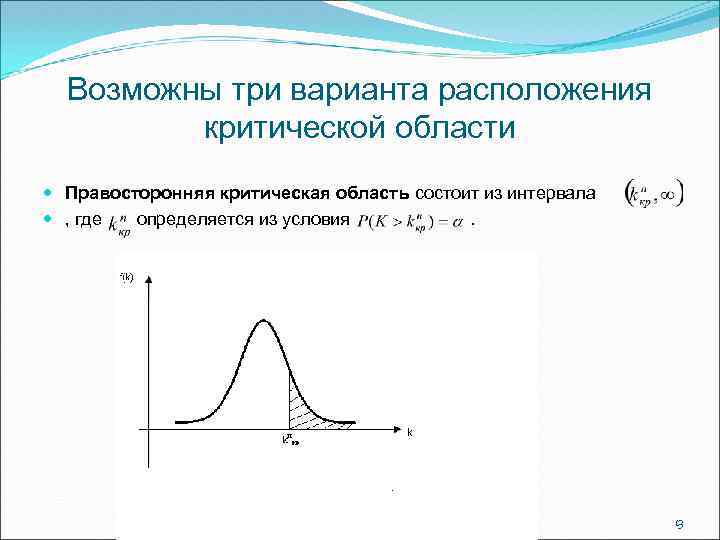Возможны три варианта расположения критической области Правосторонняя критическая область состоит из интервала , где определяется из условия. 13

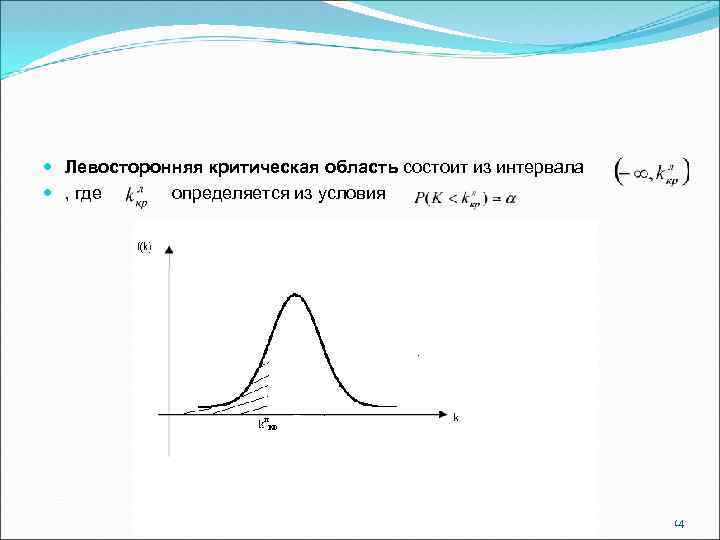Левосторонняя критическая область состоит из интервала , где определяется из условия. 14

Двусторонняя критическая область состоит из интервалов , где точки и определяются из условий: 15