ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ МАРИЯ АЛЬБЕРТОВНА ЗИРОЯН ДОКТОР ЭКОНОМИЧЕСКИХ

ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ МАРИЯ АЛЬБЕРТОВНА ЗИРОЯН ДОКТОР ЭКОНОМИЧЕСКИХ НАУК, ПРОФЕССОР КАФЕДРЫ МАТЕМАТИКИ И ИНФОРМАТИКИ

Задачи математического программирования На практике часто встречаются ситуации, когда достичь какого-то результата можно различными способами. При большом количестве способов пытаются найти наилучший. Математически это сводится к нахождению наибольшего или наименьшего значения целевой функции.

1. Задача линейного программирования Постановка задачи и графический метод решения Построим математическую модель для следующей задачи. Задача. Предположим, что некая фирма намерена построить отель на берегу моря. Отель будет состоять из номеров двух типов – люксов и номеров экономического класса. Для строительства фирма обладает капиталом 24000 условных единиц. Известно, что на строительство каждого люкса необходимо затратить 2000 у. е. , на строительство каждого номера экономического класса – 1000 уе. Предполагается, что при функционировании отеля ежедневный доход с номера-люкса составит 70 у. е. , а с номера экономического класса – 20 у. е.

Сколько номеров-люксов и номеров экономического класса должен содержать отель, чтобы обеспечить максимально возможную ежедневную выручку, если размеры отеля позволяют строить не более 10 номеров-люксов и не более 15 номеров экономического класса? Решение. Предположим, что нужно построить люксов и номеров- номеров экономического класса. Тогда ежедневная прибыль составит: При следующих ограничениях, вытекающих из условия задачи:

Полученная задача отыскания максимума прибыли при заданных ограничениях называется задачей линейного программирования (ЛП).

Определение. Общей задачей линейного программирования называется задача поиска значений переменных , при которых линейная функция принимает свое оптимальное (максимальное или минимальное) значение. При этом значения переменных должны удовлетворять системе ограничений следующего вида:

В записанной системе условия могут представлять собой как неравенства, так и уравнения. Функцию называют целевой функцией, а решение системы ограничений, при котором значение целевой функции оптимально, - оптимальным решением (оптимальным планом). В том случае, если поставленная задача содержит всего две переменных для ее решения удобно применять геометрические соображения. В этом случае в качестве ограничений рассматривают обычно условия в виде нестрогих неравенств.

Множеством решений каждого линейного неравенства системы ограничений служит на плоскости полуплоскость, рассматриваемая вместе с прямой, являющейся ее границей. Следовательно, множеством решений всей системы неравенств служит (выпуклый) многоугольник, состоящий из точек лежащих одновременно во всех , построенных полуплоскостях. Такое множество точек называется допустимой областью задачи линейного программирования.

После того, как допустимая область построена, можно ограничиться рассмотрением лишь тех точек, которые принадлежат этой области. Именно в одной из них целевая функция принимает свое максимальное (или минимальное) значение. Но таких «подозрительных» точек в общем случае все равно остается бесконечно много. Теорема. Если задача ЛП имеет оптимальное решение, то целевая функция принимает (максимальное или минимальное) угловых точек допустимой области. свое экстремальное значение в одной из

Подчеркнем, что сформулированная теорема верна лишь в том случае, когда решается задача линейного программирования, то есть когда целевая функция линейна. В случае если целевая функция не является линейной (в задаче нелинейного программирования), оптимальное решение может находиться, например, и внутри допустимой области. Из сформулированной теоремы вытекает простой алгоритм решения задачи ЛП: v Построить допустимую область. v Путем перебора угловых точек и подстановки их координат в целевую функцию определить, в какой из них целевая функция принимает максимальное (минимальное) значение.

Решаем теперь задачу, математическую модель которой мы построили в начале параграфа. Итак, при ограничениях: Для удобства пронумеруем ограничения системы неравенств и являющиеся полуплоскостей. построим на границами плоскости прямые, соответствующих

Затем с помощью полуплоскость, штриховки которая выделим ту удовлетворяет рассматриваемому условию: (1), (2), (3). Изобразим полученные прямые и полуплоскости на рисунке. Получим допустимую область, являющуюся пересечением всех построенных учитывая также условия : полуплоскостей,

Допустимая область – выпуклый многоугольник OABCD, где угловые точки имеют следующие координаты: О(0; 0), A(0; 15), B(4, 5; 15), C(10; 4), D(10; 0). Путем перебор определяем, в какой из угловых точек целевая функция принимает свое максимальное значение:

Ответ: Таким образом, оптимально, если отель будет содержать 10 люксов и 4 номера экономического класса.

Покажем теперь, как избежать полного перебора угловых точек при определении максимального (минимального) значения целевой функции. Имеем: . Утверждение. Вектор показывает направление наибольшего роста функции. В нашем примере. Это вектор сонаправлен с вектором. Строим этот вектор на координатной плоскости.

Передвигая прямую, мысленно перпендикулярную направлению градиента, в направлении стрелки, видим, что последней из угловых точек допустимой области, которые «заметает» наша прямая, является точка С. Итак, ответ: Значит в принимает этой точке и максимальное значение целевая функция.

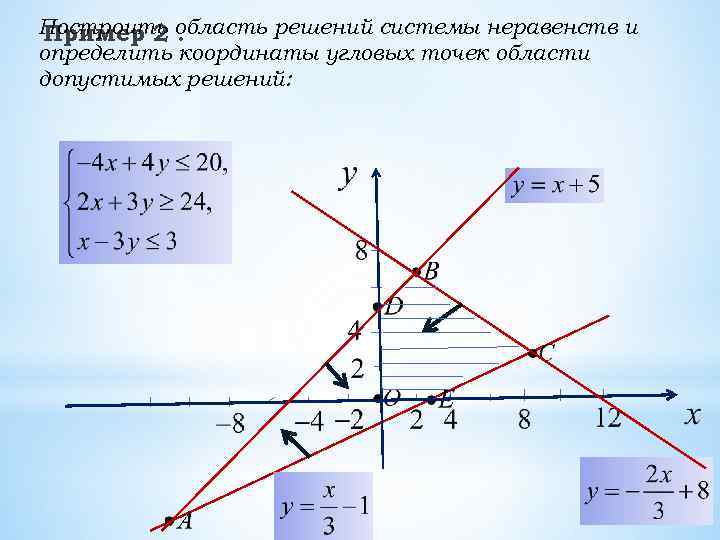
Построить область решений системы неравенств и Пример 2. определить координаты угловых точек области допустимых решений:

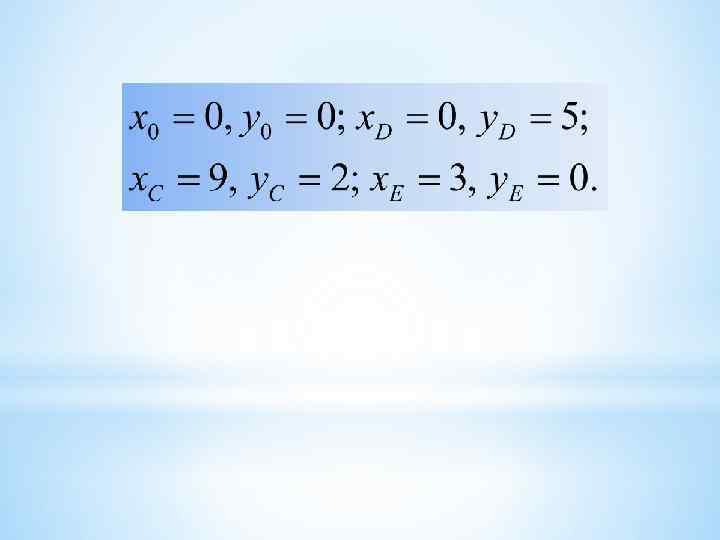
* Графический метод решения задачи линейного программирования применяется только в случае двух переменных. Постановка задачи:

Определение. Линией уровня функции называется множество всех точек функция принимает постоянное значение В случае линейной функции , в которых. все линии уровня являются прямыми, перпендикулярными общему вектору нормали , определенному соотношением Координаты вектора функции являются коэффициенты целевой.

1. 2. 3. Строится множество всех допустимых решений. Если это множество равно нулю, то задача неразрешима. Строим вектор и проводим линии уровня При увеличении прямая смещается параллельно в наплавлении вектора 4. Если А - первая точка встречи прямой уровня с областью допустимых решений, , то прямая не имеет общих точек с областью допустимых решений. Отсюда следует, что является минимальным значением целевой функции в области допустимых значений.

5. Если А - первая точка встречи прямой уровня с областью допустимых решений, является максимальным значением целевой функции в области допустимых значений. 6. Если окажется, что линия уровня параллельна одной из сторон области допустимых решений, то экстремум достигается во всех точках соответствующей стороны. Задача в этом случае имеет бесконечное число решений.

Задачи для самостоятельного решения Решить следующие задачи линейного программирования графическим методом: