Лекция_04_(ГрРешение_Алгебра).ppt
- Количество слайдов: 26

Задачи линейного программирования Линейное программирование является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач линейного программирования следующие: 1) показатель оптимальности f(X) представляет собой линейную функцию от элементов решения X = (x 1, x 2 , . . . , xn); 2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид: При этом система линейных уравнений и неравенств, определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(Х) называется целевой функцией или критерием оптимальности. 1

Если математическая модель задачи линейного программирования имеет вид: то говорят, что задача представлена в канонической форме. Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот. 2

Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот. Правило приведения задачи линейного программирования к каноническому виду состоит в следующем: 1. если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции; 2. если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1; 3. если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства; 4. если некоторая переменная xk не имеет ограничений по знаку, то она заменяется 5. (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными: , где l – свободный индекс. 3

Геометрическая интерпретация задач ЛП на плоскости Приведем геометрическую интерпретацию задачи ЛП для случая, когда число переменных равно двум. Пусть задача ЛП имеет вид: Для того, чтобы определить расположение соответствующей полуплоскости относительно граничной прямой, подставим в левую часть неравенства координаты какой-либо точки (в качестве неё проще взять начало координат), не лежащей на этой прямой. Если при такой подстановке получится верное неравенство, то область решений рассматриваемого неравенства включает подставляемую точку. Если неравенство неверное, то отмечаем штриховкой ту сторону от прямой, где нет подставляемой точки. Таким образом строится m прямых. Каждая из них определяет "допустимую" полуплоскость, где может лежать решение. Неравенства включены в общие ограничения и эти неравенства определяют первый координатный угол плоскости Часть плоскости , принадлежащая одновременно всем полуплоскостям, определяет допустимую область M решения задачи ЛП. 4

Для практического решения задачи линейного программирования на основе ее геометрической интерпретации необходимо следующее: 5

При построении допустимой области возможны три различных ситуации. 1. Допустимая область М определяется ограниченным множеством - выпуклым многогранником. Эта ситуация приведена. 2. Допустимая область М определяется неограниченным выпуклым множеством. Может оказаться, что область допустимых решений не существует(пустая), а значит система неравенств несовместная. Такой случай показан на рисунке, где нет области, лежащей одновременно по "нужную" сторону от всех прямых. Значит, и задача ЛП не имеет решения (нет допустимых решений, значит, не из чего выбирать оптимальные решения). 6

дадим геометрическую интерпретацию условию данному условию Положим сначала L =0. Построим на плоскости прямую с таким уравнением. Очевидно, что эта прямая проходит через начало координат. Если придавать L произвольные значения то прямая будет перемещаться параллельно самой себе и при перемещении в одну сторону значение L будет возрастать, в другую убывать. Вектор (с1, с2) перпендикулярен L = c 1 x 1 + c 2 x 2 и в направлении этого вектора значение L возрастает. Отметим это направление и будем вдоль него перемещать прямую L до тех пор, пока она будет сохранять общие точки с областью допустимых решений М. Могут возникнуть четыре варианта. 7
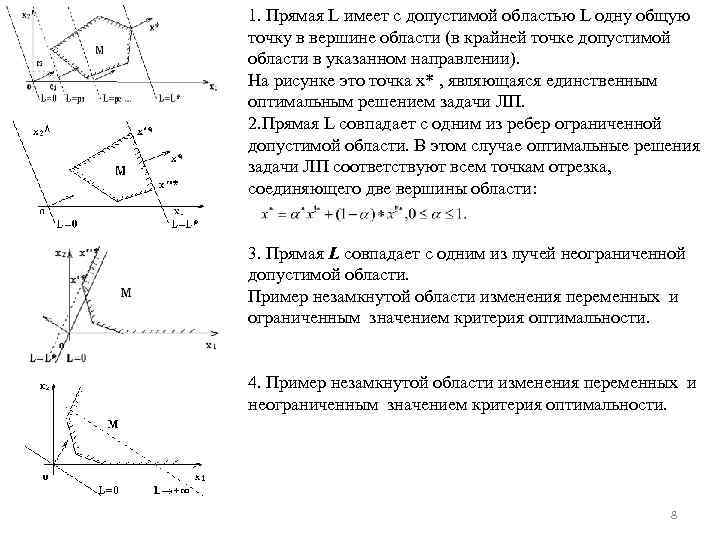
1. Прямая L имеет с допустимой областью L одну общую точку в вершине области (в крайней точке допустимой области в указанном направлении). На рисунке это точка x* , являющаяся единственным оптимальным решением задачи ЛП. 2. Прямая L совпадает с одним из ребер ограниченной допустимой области. В этом случае оптимальные решения задачи ЛП соответствуют всем точкам отрезка, соединяющего две вершины области: 3. Прямая L совпадает с одним из лучей неограниченной допустимой области. Пример незамкнутой области изменения переменных и ограниченным значением критерия оптимальности. 4. Пример незамкнутой области изменения переменных и неограниченным значением критерия оптимальности. 8

Общие рекомендации к графическому решению задач ЛП 1. Графически могут решаться: а) задачи, заданные в произвольной форме, содержащие не более двух переменных; б) задачи, заданные в канонической форме с числом свободных переменных n-m≤ 2; в) задачи в произвольной форме записи, которые после приведения к канонической форме будут содержать не более двух свободных переменных. 2. Основной формой для графического решения является 1 -й тип задач. Поэтому, если встречается 2 -й или 3 -й тип задач, то предварительно их модель должна быть приведена к 1 -му типу, а именно: к задаче на плоскости относительно свободных переменных. 3. Решение задачи 1 -го типа выполняется в два этапа. Этап 1 -построение области допустимых решений. Этап 2 - нахождение в допустимой области оптимального решения. 4. При построении области допустимых решений может встретиться один из следующих трех случаев: а) пустая область; б) выпуклый многоугольник; в) неограниченная выпуклая многоугольная область. В случае а) задача не имеет решения из-за несовместимости системы ограничений в области допустимых решений. В случае б) задача всегда имеет оптимальное решение. В случае в) в зависимости от направления вектора В (вектора коэффициентов целевой функции L) задача может иметь или не иметь решение. Последнее связано с неограниченностью функции L в области допустимых решений. 5. Если оптимальное решение существует, то возможен один из трех исходов: а) оптимальное решение единственное и совпадает с одной из вершин области; б) оптимальные решения соответствуют всем точкам отрезка, соединяющего две вершины области; в) оптимальные решения соответствуют всем точкам допустимого луча, исходящего из вершины области. 9
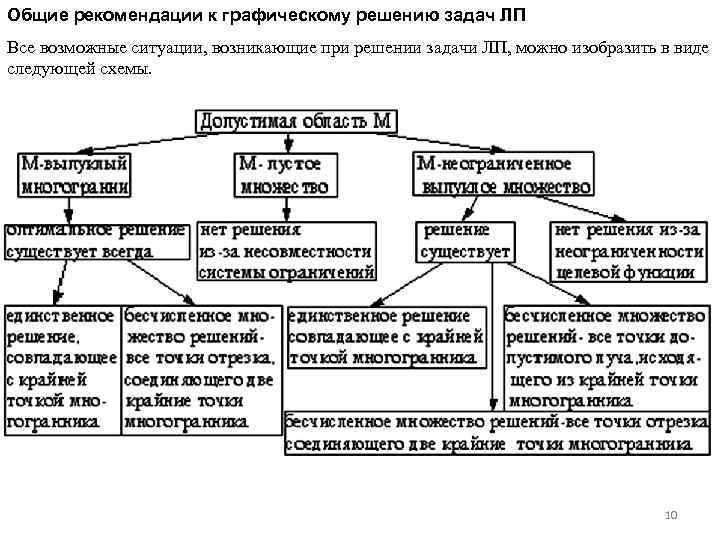
Общие рекомендации к графическому решению задач ЛП Все возможные ситуации, возникающие при решении задачи ЛП, можно изобразить в виде следующей схемы. 10

Общие рекомендации к графическому решению задач ЛП (продолжение) Для практического решения задачи линейного программирования на основе ее геометрической интерпретации необходимо следующее: 1. Построить прямые, уравнения, которых получаются в результате замены в ограничениях знаков неравенств на знаки равенств. 2. Найти полуплоскости, определяемые каждым из ограничений. 3. Определить многоугольник решений. 4. Построить вектор. 5. Построить прямую , проходящую через начало координат и перпендикулярную вектору. 6. Передвигать прямую Z в направлении вектора в результате чего либо находят точку (точки), в которой функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов. 7. Определить точки координаты максимума функции и вычислить значение целевой функции в этой точке. Областью допустимых решений системы неравенств может быть: • выпуклый многоугольник; • выпуклая многоугольная неограниченная область; • пустая область; • луч; • отрезок; • единственная точка. 11
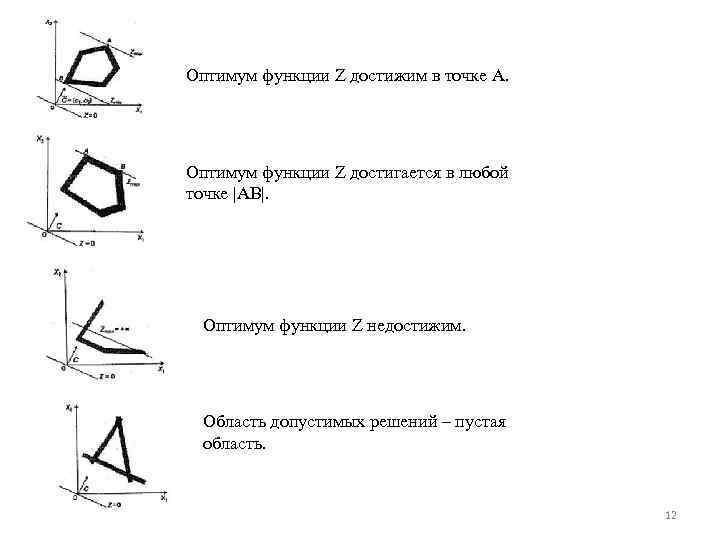
Оптимум функции Z достижим в точке А. Оптимум функции Z достигается в любой точке |АB|. Оптимум функции Z недостижим. Область допустимых решений – пустая область. 12

Симплекс-метод. Алгебра симплекс-метода Рассмотрим основную задачу линейного программирования и законы алгебраических преобразований системы ограничений и минимизируемой формы при решении задачи симплекс-методом предположим Предположим, что ранг системы меньше числа n неизвестных. Всегда можно занумеровать неизвестные так, чтобы свободными (их ровно к=п-r) оказались первые неизвестные Выражая в этом случае базисные (несвободные) неизвестные через свободные , придем к известным соотношениям: и форму F 13
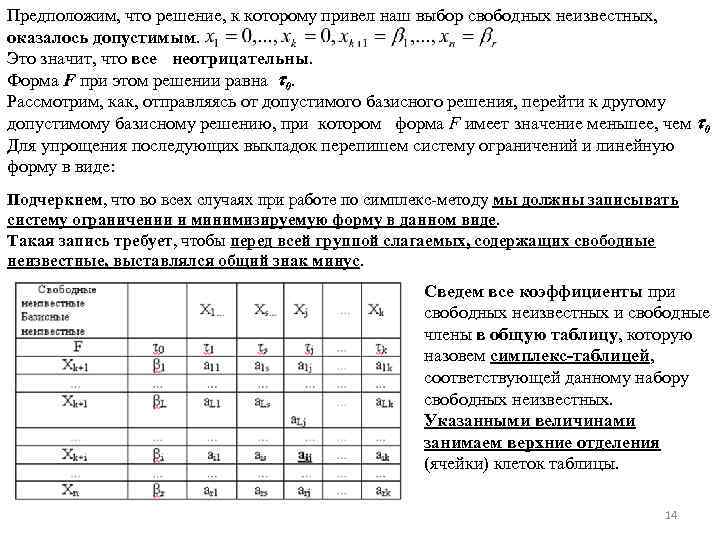
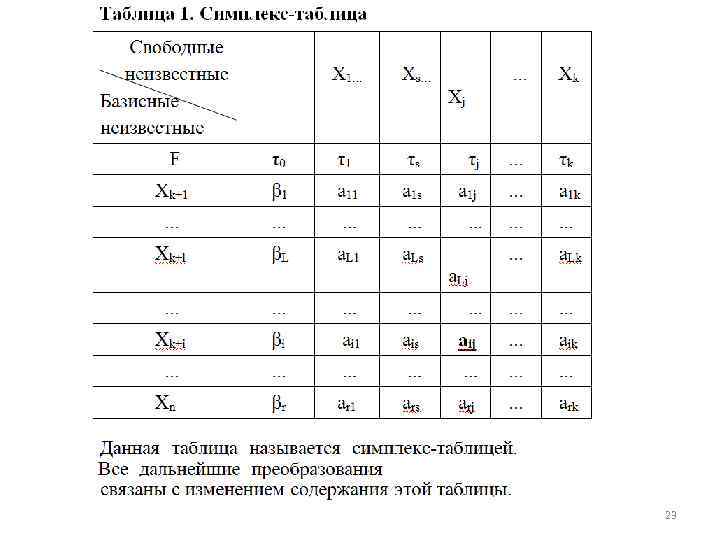
Предположим, что решение, к которому привел наш выбор свободных неизвестных, оказалось допустимым. Это значит, что все неотрицательны. Форма F при этом решении равна 0. Рассмотрим, как, отправляясь от допустимого базисного решения, перейти к другому допустимому базисному решению, при котором форма F имеет значение меньшее, чем 0 Для упрощения последующих выкладок перепишем систему ограничений и линейную форму в виде: Подчеркнем, что во всех случаях при работе по симплекс-методу мы должны записывать систему ограничении и минимизируемую форму в данном виде. Такая запись требует, чтобы перед всей группой слагаемых, содержащих свободные неизвестные, выставлялся общий знак минус. Сведем все коэффициенты при свободных неизвестных и свободные члены в общую таблицу, которую назовем симплекс-таблицей, соответствующей данному набору свободных неизвестных. Указанными величинами занимаем верхние отделения (ячейки) клеток таблицы. 14
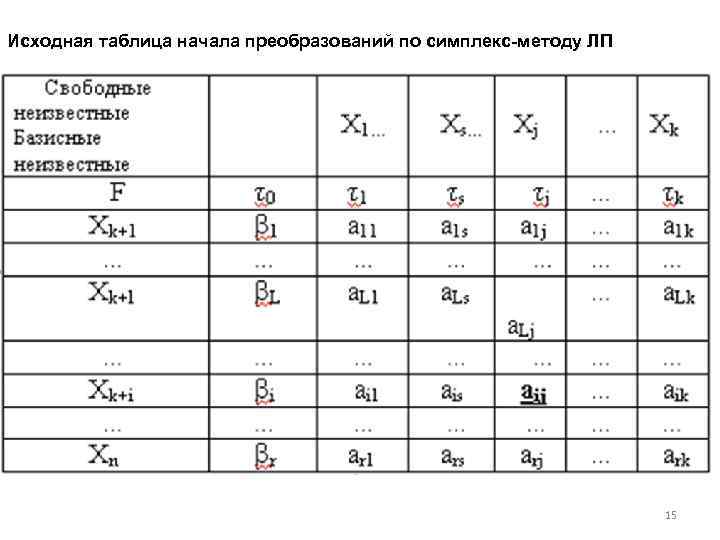
Исходная таблица начала преобразований по симплекс-методу ЛП 15

Каждая строка этой таблицы отвечает уравнению, выражающему базисные неизвестные через свободные. (Первая строка соответствует форме F). Каждый столбец отвечает некоторой свободной неизвестной, а первый столбец свободным членам (материал взят из книги Капелевич). Рассмотрим те из свободных неизвестных, которые входят в выражение формы F с положительными коэффициентами j , а, значит, в исходное выражение F с отрицательными коэффициентами j. Выберем среди рассмотренных неизвестных какую-либо одну, например xj. Если теперь сохранить за всеми свободными неизвестными, кроме xj , нулевые значения, а xj увеличивать, то форма Р будет уменьшаться. Можно увеличивать до тех пор, пока впервые не обратится в нуль какая-либо из базисных неизвестных xk+1 , …, xn. Обратимся к системе ( ). Если положить в ней все свободные неизвестные, кроме xj, равными нулю, то получим : 16

17

18

19

20

21

22
23
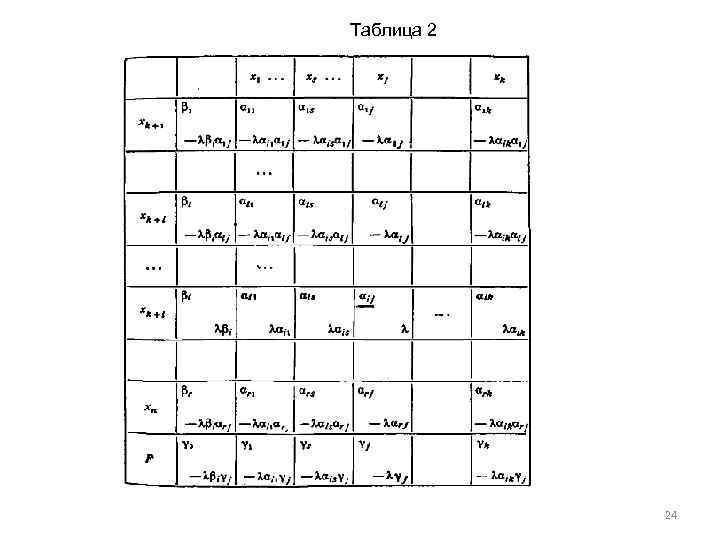
Таблица 2 24

25

26
Лекция_04_(ГрРешение_Алгебра).ppt