Задачи к главе 3 1 Задача

Задачи к главе 3 1

Задача № 3. 1. Построить конечный автомат по автоматной грамматике, построенной в задаче № 2. 5: : : = d | d | d | d | d : : =. : : = d | d : : = e : : = + | – | d : : =. : : = d | d 2

Задача № 3. 1. Решение: Сопоставим нетерминалам грамматики состояния автомата и введем еще одно дополнительное состояние A — единственное конечное состояние. Если B a. C — правило, то соединим вершину B с вершиной C ориентированной дугой, помеченной терминалом a. Если B a — правило, то соединим вершину B с вершиной A ориентированной дугой, помеченной терминалом a. Полученная диаграмма переходов — один из способов представления конечного автомата. Как видим, она представляет недетерминированный конечный автомат. 3

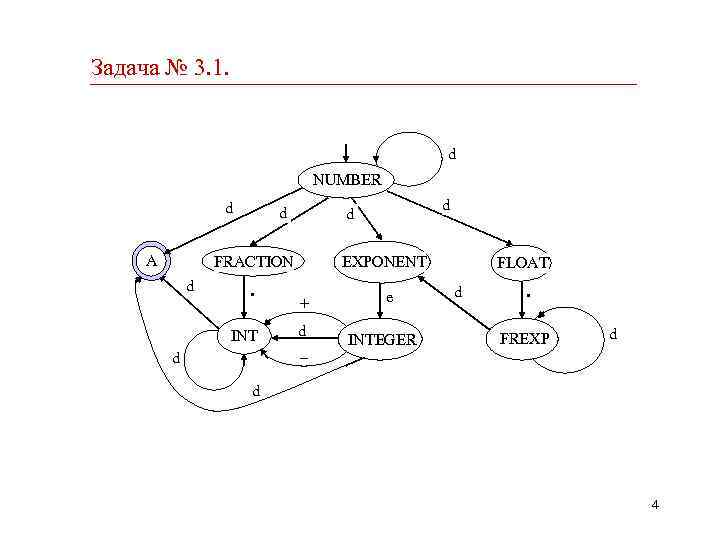Задача № 3. 1. d NUMBER d A d FRACTION d . INT d d d EXPONENT + d e INTEGER FLOAT d . FREXP d – d 4

Задача № 3. 1. В формальных обозначениях fa M = (Q, , , q 0, F), где Q = {NUMBER, FRACTION, EXPONENT, FLOAT, INTEGER, FREXP, A}, = {d , . , e , + , – }; (NUMBER, d) = {A, FRACTION, EXPONENT, FLOAT, NUMBER}, (FRACTION, . ) = {INT}, (EXPONENT, e) = {INTEGER}, (FLOAT, . ) = {FREXP}, (FREXP, d) = {FREXP, EXPONENT}, (INT, d) = {INT, A}, (INTEGER, ±) = {INT}; q 0 = NUMBER; F = {A}. 5

Задача № 3. 2. Построить детерминированный конечный автомат, эквивалентный недетерминированному автомату, построенному в задаче 3. 1. 6

Задача № 3. 2. В формальных обозначениях fa M = (Q, , , q 0, F), где Q = {[NUMBER], [A, FRACTION, EXPONENT, FLOAT, NUMBER], [INT, FREXP], [INTEGER], [INT, FREXP, EXPONENT], [A, INT], [ INT], }; = {d , . , e , + , – }; ([NUMBER], d) = [A, FRACTION, EXPONENT, FLOAT, NUMBER], ([A, FRACTION, EXPONENT, FLOAT, NUMBER], . ) = [INT, FREXP], ([A, FRACTION, EXPONENT, FLOAT, NUMBER], e) = [INTEGER], ([INT, FREXP], d) = [INT, FREXP, EXPONENT], ([INTEGER], d) = [INT, A], ([INTEGER], ±) = [INT], ([INT, FREXP, EXPONENT], d) = [INT, FREXP, EXPONENT], ([INT, FREXP, EXPONENT], e) = [INTEGER]; ([A, INT], d) = [A, INT], ([INT], d) = [A, INT]; q 0 = [NUMBER]; F = {[A, FRACTION, EXPONENT, FLOAT, NUMBER], [A, INT, FREXP, EXPONENT], [A, INT]}. 7

Задача № 3. 2. Перенумеровав состояния следующим образом: q 0 = [NUMBER], q 1 = [A, FRACTION, EXPONENT, FLOAT, NUMBER], q 2 = [INT, FREXP], q 3 = [INTEGER], q 4 = [A, INT, FREXP, EXPONENT], q 5 = [A, INT], q 6 = [INT]}, Таблица получаем dfa M = (Q, , , q 0, F), где Q = {q 0 , q 1, q 2, q 3, q 4, q 5, q 6}; = {d , . , e , + , – }; F = {q 1, q 4, q 5}. Return to slade 10 Return to slade 11 8

Задача № 3. 3. По детерминированному конечному автомату, построенному в задаче 3. 2, построить эквивалентную автоматную грамматику. 9

Задача № 3. 3. Решение: q 0 d q 1 . q 2 eq 3 q 2 d q 4 d q 3 d q 5 ± q 6 d q 4 eq 3 d q 5 d q 6 d q 5 d 10

Задача № 3. 4. По автоматной грамматике, полученной в задаче 3. 3 построить регулярное эквивалентное выражение. 11

Задача № 3. 4. Решение: q 0 d q 1 d = d+ d+e (d+ ±d+ ) d+. d+e (d+ ± d+ ) q 1 d q 1 . q 2 eq 3 = d* (. d+e (d+ ± d+ ) . d+ e (d+ ±d+ ) ) q 2 d q 4 d = d+ e (d+ ± d+ ) d+ q 3 d q 5 ± q 6 d = dd+ ± d+ d = d+ ± d+ q 4 d q 4 eq 3 d = d*(e (d+ ± d+ ) d ) q 5 d = d+ q 6 d q 5 d = d+ Окончательный ответ: L = d+ [. d+] [e [±]d+ ]. 12

Задача № 3. 5. Докажите, что dfa M, построенный в задаче 3. 2, содержащий 7 состояний, является минимальным. 13

Задача № 3. 5. Из теоремы о существовании единственного fa с минимальным числом состояний следует, то состояния p и q эквивалентны, в том, и только в том случае, если (1) (p F q F) и при этом (2) множества символов, допустимых в состояниях p и q, равны, причем, если (p, a) = p 1 и (q, a) = q 1, где a — любой символ, допустимый в этих состояниях, то состояния p 1 и q 1 тоже эквивалентны. Применив это определение к состояниям fa M из задачи 3. 2 получаем, что это минимальный по числу состояний автомат. 14

Задача № 3. 6. По конечному автомату M из задачи 3. 2 построить эквивалентную грамматику типа 3. 15

Задача № 3. 6. Положим G = (VN, VT, P, S), где VN = {q 0, q 1, q 2, q 3, q 4, q 5, q 6}; VT = {d , . , e , + , – }; P = {q 0 dq 1, q 0 d, q 1 dq 0, q 1 . q 2, q 1 eq 3, q 2 dq 4, q 3 dq 5, q 3 d, q 3 q 6, q 4 dq 4, q 4 eq 3, q 5 dq 5, q 5 d, q 6 dq 5}; S = q 0. 16

Задача № 3. 7 Доказать, что если L — регулярное множество, то LR = {w. R | w L} — тоже регулярное множество. 17

Задача № 3. 7 Решение: L — rs, т. е. cуществует dfa M = (Q, , , q 0, F) такой, что T(M) = L. Если предположить, что M имеет единственное конечное состояние qf, то можно построить ndfa MR = (QR, , R, q 0 R, FR ), просто сделав конечное состояние fa M начальным состоянием fa MR, начальное состояние fa M единственным конечным состоянием fa MR и обратив стрелки в диаграмме состояний исходного автомата M, т. е. QR = Q, q 0 R = qf , FR ={q 0}, q R(p, a), если (q, a) = p. Если же fa M имеет несколько конечных состояний, то надо построить новое начальное состояние fa MR, соединив его с теми состояниями исходного fa M, из которых этот последний переходил в свои конечные состояния по соответствующим символам. Именно, QR = Q {q 0 R}, q 0 R Q, FR ={q 0}, 1) q R(p, a), если (q, a) = p, где q, p Q, a и 2) q R(q 0 R, a), если (q, a) = p и p F, q Q, a . Замечание. Построенный автомат в общем случае неприведенный. 18

Задача № 3. 8 Пусть G = (VN, VT, P, S) — грамматика, каждое правило которой имеет вид: A a или A Ba, где A, B VN, a VT. Доказать, что L = L(G) — rs. 19

Задача № 3. 8 Решение: Достаточно обратить внимание на то, что дерево вывода в такой грамматике является зеркальным отражением дерева вывода в грамматике G 1, получающейся из данной перестановкой символов в правой части правил A Ba исходной грамматики. Очевидно, что G 1 — регулярная грамматика, и L(G 1) = L R. Утверждение, которое требуется доказать, непосредственно следует из решения задачи № 3. 5. 20

Задача № 3. 9 Пусть L — rs. Доказать, что L 1 = {x | xy L} — rs. 21

Задача № 3. 9 Решение: Пусть M = (Q, , , q 0, F) — fa и L = T(M). Положим M 1 = (Q 1, 1, q 1, F 1), где Q 1 = Q, 1 = , q 1 = q 0, 1(q, a) = (q, a) для q Q, a ; F 1 = Q. Очевидно, что любой префикс, включая пустой, цепочки из языка L принимается fa M 1. Замечание. Такое решение применимо, если автомат M — приведенный: по крайней мере любое его состояние участвует в распознавании хотя бы одной цепочки из T(M). 22

Задача № 3. 10 Дан: fa M = (Q, , , q 0, F) — fa и L = T(M). Найти: fa M 1 = (Q 1, , 1, q 1, F 1) такой, что T(M 1) = L и, если q Q 1, то существует такая цепочка xy L, что (q 1, xy) (q, y) (p, ), где p F 1. 23

Задача № 3. 10 Решение: Прежде всего следует найти все достижимые состояния Qd из Q. Для этого: 1) инициировать множество Qd = {q 0}. 2) Далее множество Qd пополняется: если q Qd и p (q, a) для некоторого a , то Qd = Qd {p}. 3) Шаг 2 повторяется до тех пор, пока множество Qd не перестанет пополняться. После этого построим подмножество состояний из Qd , из которых достижимо какое-нибудь конечное состояние из F Qd. Для этого: 4) Q 1 = F Qd. 5) Далее множество Q 1 пополняется: если q Q 1 и q (p, a) для некоторого a , то Q 1 = Q 1 {p}. 6) Шаг 5 повторяется до тех пор, пока множество Q 1 не перестанет пополняться. 7) Наконец, F 1 = F Qd и 1 получается, если из исключить равенства, в которых участвуют состояния из Q Q 1. 24

Задача № 3. 11 Построить fa, распознающий язык L = {w | w {0 , 1}* и w не содержит двух последовательных единиц}. 25

Задача № 3. 11 Решение: Положим fa M = (Q, , , q 0, F), где Q = {q 0, q 1, q 2, q 3, q 4}, = {0, 1}, (q 0 , 0) = q 1, (q 0 , 1) = q 3, (q 1 , 0) = q 1, (q 1 , 1) = q 2, (q 2 , 0) = q 1, (q 3 , 0) = q 4, (q 4 , 1) = q 3, F = {q 0, q 1, q 2, q 3, q 4}. Очевидно, построенный fa M является ndfa (см. значения (q 2 , 0)). 1 Диаграмма переходов. 26

Задача № 3. 12* Построить регулярную грамматику, порождающую язык L = {x x {0, 1}*, где x не содержит двух единиц подряд}. 27

Задача № 3. 13* Пусть G — грамматика, в которой все правила имеют вид: A x. B и A x, где A и B — нетерминалы, а x — не пустая терминальная цепочка. Покажите, что L(G) может быть порожден регулярнной грамматикой. 28