Задачи к главе 2 1
Задача № 2. 1 Дана неукорачивающая грамматика G = (VN, VT, P, S), где VN = {S, B, C}, VT = {a, b, c}, P = { (1) S a. SBC, (2) S a. BC, (3) CB BC, (4) a. B ab, (5) b. B bb, (6) b. C bc, (7) c. C cc}. Построить НС-грамматику, эквивалентную данной. 2
Задача № 2. 1 Решение: Все правила, кроме (3), не нуждаются ни в каких преобразованиях, т. к. уже соответствуют требованиям НСграмматики. Правило (3) заменим в группой правил: (3. 1) CB A 1 B, (3. 2) A 1 B A 1 A 2, (3. 3) A 1 A 2 BA 2, (3. 4) BA 2 BC, все из которых так же соответствуют требованиям НСграмматики. Эти правила не для чего, кроме как для вывода: CB A 1 A 2 BC служить не могут. В них A 1 и A 2 новые нетерминалы. 3
Задача 2. 2 Дана контекстно-свободная грамматика G = (VN, VT, P, S), где VN = {S, A, B}, VT={a, b}, P ={S a. B, S b. A, A a. S, A b. AA, B b. S, B a. BB}. Какой язык она порождает? 4
Задача 2. 2 Решение: Индукцией по длине цепочки покажем, что L(G) = {x {a, b}+ #a x = #b x}, где #a x обозначает число букв а в цепочке x, а #b x — число букв b. Другими словами, язык, порождаемый этой грамматикой, состоит из непустых цепочек, в которых число букв а и b одинаково. Достаточно доказать, что для x VT+ 1) S x тогда и только тогда, когда цепочка x состоит из равного числа букв a и b; 2) A x тогда и только тогда, когда x имеет на одно a больше, чем b; 3) B x тогда и только тогда, когда x имеет на одно b больше, чем a. База. Очевидно, что все три утверждения выполняются для всех x: x = 1, поскольку A a, B b и никакая терминальная цепочка не выводима из S. Кроме того, никакие строки единичной длины, отличающиеся от a и b, не выводимы из A и B соответственно. 5
Задача 2. 2 Индукционная гипотеза. Предположим, что утверждения 1– 3 выполняются для всех x: x k (k 1). Индукционный переход. Покажем, что они истинны для x: x = k + 1. Необходимость. Если S x, то вывод должен начинаться либо с правила S a. B, либо с правила S b. A. В первом случае x = ax 1, причем x 1 = k и B x 1. По индукционному предположению число букв b в цепочке x 1 на единицу больше, чем число букв a, так что в цепочке x букв a столько же, сколько букв b. Аналогичное рассуждение достигает цели, если вывод начинается с правила S b. A. 6
Задача 2. 2 Достаточность. Теперь нужно доказать обратное утверждение, т. е. что если x = k + 1 и #a x = #b x, то S x. Либо первый символ x есть a, либо он есть b. Предположим, что x = ax 1. Теперь x 1 = k и цепочка x 1 имеет на одну букву b больше, чем букв a. По индукционной гипотезе B x 1. Но тогда S a. B ax 1= x. Аналогичное рассуждение достигает цели, если первый символ x есть b. Для завершения доказательства аналогичным образом должны быть доказаны утверждения 2 и 3. 7
Задача 2. 3 Рассмотрим грамматику G = (VN, VT, P, S), где VN = {S, A, B}, VT={0, 1}, P = {S 0 A, S 1 B, S 0, A 0 A, A 0 S, A 1 B, B 1, B 0}. Ясно, что G — регулярная грамматика. Вопрос: Определить, какой язык порождает данная грамматика? 8
Задача № 2. 4 Написать КС-грамматику, порождающую числа без знака языка программирования Паскаль. Пояснение: Образцы чисел: 0, 25, и. т. д. — целые; 0. 3, 3. 14 и т. д. — дробные; 3. 14 e 00, 0. 314 e+1, 314 e– 02 и т. д — с плавающей запятой. 10
Задача № 2. 5 Написать автоматную грамматику, порождающую числа без знака языка Паскаль. Retrun to slade 3. 2 12
Задача № 2. 5 Решение:
Задача № 2. 6 Какой язык порождает cfg G = (VN, VT, P, S), где VN = {E}; VT = {a, +, *}; P = {E a, E E + E, E E * E}; S = E? Какие недостатки этой грамматики? 14
Задача № 2. 7 Построить cfg, порождающую выражения (например, арифметические). Проверить, сохраняет ли построенная грамматика информацию о порядке их вычисления. 17
Задача № 2. 7 Решение: G = (VN, VT, P, S), где VN = {E, T, F}; VT = {a, +, *, (, )}; P ={ (1) E E + T, (2) E T, (3) T T * F, (4) T F, (5) F a, (6) F (E)}; S = E. 18
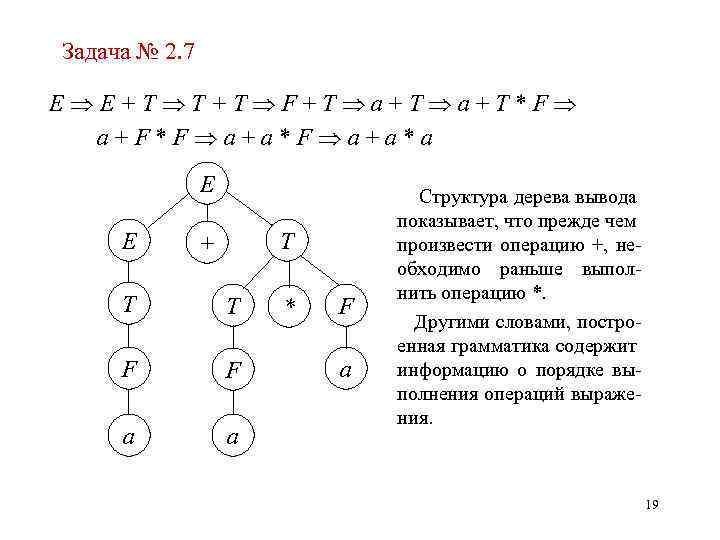Задача № 2. 7 E E+T T+T F+T a+T*F a+F*F a+a*a E E T + T T F F a a * F a Структура дерева вывода показывает, что прежде чем произвести операцию +, необходимо раньше выполнить операцию *. Другими словами, построенная грамматика содержит информацию о порядке выполнения операций выражения. 19
Задача № 2. 8 Построить cfg, порождающую выражения (например, арифметические) без “лишних” скобок. Пояснение. Скобки “лишние”, если их можно восстановить по приоритетам операций или в соответствии с правилом: “вычислять выражения с операциями одинакового старшинства слева направо”. 20
Задача № 2. 8 Решение: Схема рассуждений может быть представлена в следующем виде: F 1 ( F 1) (F 1) F 2 F 1 F 2 F 2 ( F 2 ) F 3 A 1 + A 2 F 3 A 2 * A 3 F 3 F 4 F 4 F 4 a a ( F 1) F 4 – A 2 ( F 1) ( F 2 ) ( F 3 ) F 4 a A 1 : : = F 1 F 2 F 3 F 4 a A 2 : : = (F 1) F 2 F 3 F 4 a A 3 : : = (F 1) ( F 2 ) F 3 F 4 a A 4 : : = (F 1) ( F 2 ) ( F 3 ) F 4 a A 1 — начальный нетерминал. F 3 ( F 2 ) A 2 ^ A 3 ( F 3 ) a F 1 : : = A 1 + A 2 F 2 : : = A 2 * A 3 F 3 : : = A 3 ^ A 4 F 4 : : = – A 4 F 4 a 21
Задача № 2. 9 Написать регулярную грамматику, порождающую язык L = {w | w {0 , 1}* и w не содержит двух последовательных единиц}. 22
Задача № 2. 9 Решение: G = (VN, VT, P, S), где VN = {S, A , B , C , D}, VT = {0, 1}, P = {S , S 0, S 1, S 0 A, S 1 B, A 0 A, A 1, A 1 C, B 0 D, C 0 C, D 0 D, D 1 B}. 23
Задача № 2. 10 Построить cfg, порождающую язык L = {w | w {a, b}*, где #a w = 2 #b w }. 24
Задача № 2. 10 Решение: G = (VN, VT, P, S), где VN = {S}, VT = {a, b}, P = {S aab | aba | baa | Saab | Saba | Sbaa | a. Sab | a. Sba | b. Saa | aa. Sb | ab. Sa | ba. Sa | aab. S | aba. S | baa. S}. 25
Задача № 2. 11 Построить csg, порождающую язык L = {w | w {a, b, c}*, где #a w = #b w = #c w }. 26
Задача № 2. 11 Решение: G = (VN, VT, P, S), где VN = {S, A, B, C}, VT = {a, b, c}, P = {S a. SBC | b. SCA | c. SAB | | BC CB | CA AC | AB BA | a. B ab | a. C ac | b. A ba | b. C bc | c. A ca | c. B cb}. 27
Задача № 2. 12 Построить csg, порождающую язык L = {w w | w {0, 1}*}, т. е. L — все слова в {0, 1}*, длины которых четны, и первые и последние половины которых равны. 28
Задача № 2. 12 Решение: G = (VN, VT, P, S), где VN = {S, A, B, N, U}, VT = {0, 1}, P = { (Продолжение прототипа: ) S 0 SA | 1 SB | 0 A | 1 B | (Движение налево: ) 0 A AN | 1 A AU | 0 B BN | 1 B BU | (Движение направо: ) AN 0 N | AU 0 U | BN 1 N | BU 1 U | 0 N 00 | 1 N 10 | 0 U 01 | 1 U 11}. 29
Задача № 2. 12 (1) S 0 A AN 00. (2) S 1 B BU 11. (3) S 0 SA 01 SBA 011 BBA (налево: ) 01 BUBA 0 BUUBA BNUUBA (направо: ) 1 NUUBA 101 UBA 1011 BA (налево: ) 101 BUA 10 BUUA 1 BNUUA BUNUUA (направо: ) 1 UNUUA 110 UUA 11011 A (налево: ) 1101 AU 110 AUU 11 ANUU 1 AUNUU AUUNUU (направо: ) 0 UUNUU 011 NUU 01101 U 011011. 30
Задача № 2. 12 Пусть мы имеем сентенциальную форму— прототип 1) 011 -BBA Налево: 9) 101 -BUA 18) 110 -1 AU 2) 01 B-UBA 10) 10 B-UUA 19) 110 -AUU 3) 0 BU-UBA 11) 1 BN-UUA 20) 11 A-NUU 4) BNU-UBA 12) BUN-UUA 21) 1 AU-NUU -----------------22) AUU-NUU Направо: ---------5) 1 NU-UBA 13) 1 UN-UUA Направо: 6) 10 U-UBA 14) 11 N-UUA 23) 0 UU-NUU 7) 101 -UBA 15) 110 -UUA 24) 01 U-NUU 8) 101 -1 BA 16) 110 -1 UA 25) 011 -NUU --------17) 110 -11 A 26) 011 -0 UU ---------27) 011 -01 U 28) 011 -011 31
Задача № 2. 13* Построить магазинный преобразователь P, реализующий трансляцию: (P) ={( x, y) x {a, b}+ ; y = ci, i = #a x – #b x }. 32
Задача № 2. 14* Построить КС-грамматику, порождающую язык L = { x x {a, b}*, #a x = 2 * #b x}. 33