 Задачи к главам 6 и 7 1
Задачи к главам 6 и 7 1
 Задача № 6. 1. Построить машину Тьюринга, которая распознает язык L={wcw | w {a, b}+}. 2
Задача № 6. 1. Построить машину Тьюринга, которая распознает язык L={wcw | w {a, b}+}. 2
 Задача № 6. 2. Пусть Tm T = ({q 0, q 1, q 2, q 3}, {¢ , [, ], X, B)}, , {q 3}), где (q 0, ¢) = (q 0, ¢, R) (q 1, ]) = (q 2, X, L) (q 0, X) = (q 0, X, R) (q 2, a) = (q 2, a, L) для всех a ¢ (q 0, [) = (q 1, X, R) (q 2, ¢) = (q 0, ¢, R) (q 1, [) = (q 1, [, R) (q 0, B) = (q 3, X, R) (q 1, X) = (q 1, X, R) Какие слова вида ¢w, где w {[, ]}*, принимаются Tm T? Используете алгоритм теоремы 7. 4 для того, чтобы найти грамматику, порождающую язык, распознаваемый Tm T. Можете ли вы построить более простую грамматику для этого языка ? 3
Задача № 6. 2. Пусть Tm T = ({q 0, q 1, q 2, q 3}, {¢ , [, ], X, B)}, , {q 3}), где (q 0, ¢) = (q 0, ¢, R) (q 1, ]) = (q 2, X, L) (q 0, X) = (q 0, X, R) (q 2, a) = (q 2, a, L) для всех a ¢ (q 0, [) = (q 1, X, R) (q 2, ¢) = (q 0, ¢, R) (q 1, [) = (q 1, [, R) (q 0, B) = (q 3, X, R) (q 1, X) = (q 1, X, R) Какие слова вида ¢w, где w {[, ]}*, принимаются Tm T? Используете алгоритм теоремы 7. 4 для того, чтобы найти грамматику, порождающую язык, распознаваемый Tm T. Можете ли вы построить более простую грамматику для этого языка ? 3
 Задача № 6. 2. Решение: Ясно, что цепочка w должна состоять из нуля или большего числа парных скобок [ ], внутри которых могут находиться такие же вложения. 3 4 Например, [ ] [ ] ] 1 2 Данная Tm еще принимает ¢+BB … 4
Задача № 6. 2. Решение: Ясно, что цепочка w должна состоять из нуля или большего числа парных скобок [ ], внутри которых могут находиться такие же вложения. 3 4 Например, [ ] [ ] ] 1 2 Данная Tm еще принимает ¢+BB … 4
 Задача № 6. 2. Простая грамматика L(T): S ¢A A ¢A W W BW B [ ] [W ] Например, S ¢A ¢W ¢BW ¢ [ ]BW ¢ [ ] [ B ]W ¢ [ ] [ [ ] ]. 5
Задача № 6. 2. Простая грамматика L(T): S ¢A A ¢A W W BW B [ ] [W ] Например, S ¢A ¢W ¢BW ¢ [ ]BW ¢ [ ] [ B ]W ¢ [ ] [ [ ] ]. 5
 Задача № 6. 3. Пусть G = ({A, B}, {a, b}, P, A), где P = {A Ba, Aa Bb, B b. A, Ab , B BB, B b, A a}. Каков язык L(G)? Построить Tm, распознающую L(G). Является ли язык L(G) контекстно-свободным или регулярным? 6
Задача № 6. 3. Пусть G = ({A, B}, {a, b}, P, A), где P = {A Ba, Aa Bb, B b. A, Ab , B BB, B b, A a}. Каков язык L(G)? Построить Tm, распознающую L(G). Является ли язык L(G) контекстно-свободным или регулярным? 6
 Задача № 6. 3. Решение: P = {(1) A Ba, (2) Aa Bb, (3) B b. A, (4) Ab , (5) B BB, (6) B b, (7) A a}. (1) Начало вывода: A Ba. Далее возможны три продолжения: (3 ) b 2 n. Abn (4) bb. Ab bb (5) (n-2) (6) n (5) n b bn+2 (n 1) b. Bb b. B (2 ) ) (6 bbb b. Aa bn. Aan (n 1) (5) (n-1) n (6) n Ba (1) (3 ) (7) ba A Ba ) a (6 (7) bna (n 1) 7
Задача № 6. 3. Решение: P = {(1) A Ba, (2) Aa Bb, (3) B b. A, (4) Ab , (5) B BB, (6) B b, (7) A a}. (1) Начало вывода: A Ba. Далее возможны три продолжения: (3 ) b 2 n. Abn (4) bb. Ab bb (5) (n-2) (6) n (5) n b bn+2 (n 1) b. Bb b. B (2 ) ) (6 bbb b. Aa bn. Aan (n 1) (5) (n-1) n (6) n Ba (1) (3 ) (7) ba A Ba ) a (6 (7) bna (n 1) 7
 Задача № 6. 3. * A (a | bn+2 | bb) | bn. Aan | b 2 n. A bn (n 1) * A {bm (a | bn+2 | bb) am} {b 2 m (a | bn+2 | bb) bm } (n 1, m 0). (a | bn+2 | bb) = b*a | b+bb L = {bm (b*a | b+bb) am | m 0} {b 2 m (b*a | b+bb) bm | m 0 }. {bm (b*a | b+bb) am | m 0} = { b*a + | b* bbba* } {b 2 m (b*a | b+bb) bm | m 0 } = {b*a b* | b* bbb}. L = { b*a + | b* bbba* | b*a b* | b* bbb} = { b*a + | b* bbba* | b*a b* }. 8
Задача № 6. 3. * A (a | bn+2 | bb) | bn. Aan | b 2 n. A bn (n 1) * A {bm (a | bn+2 | bb) am} {b 2 m (a | bn+2 | bb) bm } (n 1, m 0). (a | bn+2 | bb) = b*a | b+bb L = {bm (b*a | b+bb) am | m 0} {b 2 m (b*a | b+bb) bm | m 0 }. {bm (b*a | b+bb) am | m 0} = { b*a + | b* bbba* } {b 2 m (b*a | b+bb) bm | m 0 } = {b*a b* | b* bbb}. L = { b*a + | b* bbba* | b*a b* | b* bbb} = { b*a + | b* bbba* | b*a b* }. 8
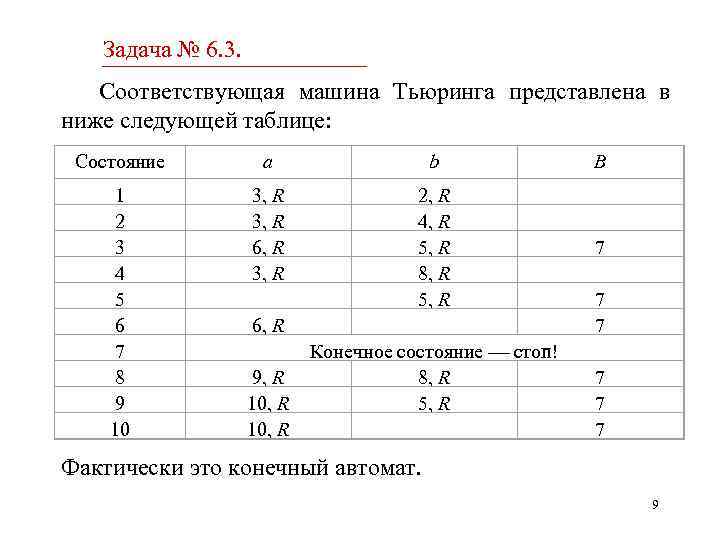 Задача № 6. 3. Соответствующая машина Тьюринга представлена в ниже следующей таблице: Состояние a b B 1 2 3 4 5 6 7 8 9 10 3, R 6, R 3, R 6, R 2, R 4, R 5, R 8, R 5, R Конечное состояние стоп! 8, R 5, R 7 7 7 9, R 10, R 7 7 7 Фактически это конечный автомат. 9
Задача № 6. 3. Соответствующая машина Тьюринга представлена в ниже следующей таблице: Состояние a b B 1 2 3 4 5 6 7 8 9 10 3, R 6, R 3, R 6, R 2, R 4, R 5, R 8, R 5, R Конечное состояние стоп! 8, R 5, R 7 7 7 9, R 10, R 7 7 7 Фактически это конечный автомат. 9