В9 задачи ЕГЭ 2013 по теме цилиндр.pptx
- Количество слайдов: 24
 Задачи ЕГЭ 2010 «Цилиндр. Конус» Задания части В Задания части С Учитель математики Ларькина Галина Александровна школа № 91 г. Нижнего Новгорода
Задачи ЕГЭ 2010 «Цилиндр. Конус» Задания части В Задания части С Учитель математики Ларькина Галина Александровна школа № 91 г. Нижнего Новгорода
 Задания части В Площадь поверхности • № 1, 2 В-9 (цилиндр) • № 3 В-9 (цилиндр) • № 9 (конус) • № 10 (конус) • № 11 (цилиндр) Объем • № 4 (цилиндр) • № 5 (цилиндр и конус) • № 6 (цилиндр и конус) • № 7 (цилиндр и конус) • № 8 (цилиндр и конус) В главное меню
Задания части В Площадь поверхности • № 1, 2 В-9 (цилиндр) • № 3 В-9 (цилиндр) • № 9 (конус) • № 10 (конус) • № 11 (цилиндр) Объем • № 4 (цилиндр) • № 5 (цилиндр и конус) • № 6 (цилиндр и конус) • № 7 (цилиндр и конус) • № 8 (цилиндр и конус) В главное меню
 № 1, 2 • Площадь боковой поверхности цилиндра равна 80π, а диаметр основания равен 8. Найдите длину образующей цилиндра. Ответ: 10 В-9 • Площадь боковой поверхности цилиндра равна 60π, а радиус основания равен 5. Найдите длину образующей цилиндра. Ответ: 6 В меню
№ 1, 2 • Площадь боковой поверхности цилиндра равна 80π, а диаметр основания равен 8. Найдите длину образующей цилиндра. Ответ: 10 В-9 • Площадь боковой поверхности цилиндра равна 60π, а радиус основания равен 5. Найдите длину образующей цилиндра. Ответ: 6 В меню
 № 3 В-9 • Хорда основания цилиндра стягивает дугу в 600. Секущая плоскость содержит эту хорду и параллельна высоте цилиндра. Площадь сечения равна 20. Вычислите площадь боковой поверхности цилиндра. О 1 Ответ: 40π А О Решение В В меню
№ 3 В-9 • Хорда основания цилиндра стягивает дугу в 600. Секущая плоскость содержит эту хорду и параллельна высоте цилиндра. Площадь сечения равна 20. Вычислите площадь боковой поверхности цилиндра. О 1 Ответ: 40π А О Решение В В меню
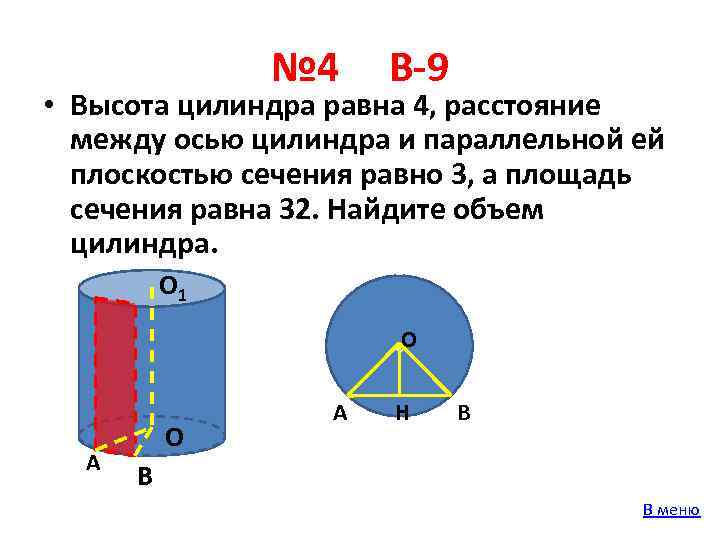 № 4 В-9 • Высота цилиндра равна 4, расстояние между осью цилиндра и параллельной ей плоскостью сечения равно 3, а площадь сечения равна 32. Найдите объем цилиндра. О 1 о. О А Н В В В меню
№ 4 В-9 • Высота цилиндра равна 4, расстояние между осью цилиндра и параллельной ей плоскостью сечения равно 3, а площадь сечения равна 32. Найдите объем цилиндра. О 1 о. О А Н В В В меню
 № 5 В-9 Объем цилиндра равен 12 см 3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню
№ 5 В-9 Объем цилиндра равен 12 см 3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню
 № 6 В-9 Объем цилиндра равен 12 см 3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню
№ 6 В-9 Объем цилиндра равен 12 см 3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню
 № 7 В-9 Объем конуса равен 6 см 3. Чему равен объем цилиндра, который имеет такое же основание и такую же высоту, как и данный конус? Ответ: 18 В меню
№ 7 В-9 Объем конуса равен 6 см 3. Чему равен объем цилиндра, который имеет такое же основание и такую же высоту, как и данный конус? Ответ: 18 В меню
 № 8 В-9 Объем цилиндра равен 12 см 3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню
№ 8 В-9 Объем цилиндра равен 12 см 3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню
 № 9 В-9 Радиус основания первого конуса в 2 раза меньше, чем радиус основания второго конуса, а образующая первого конуса в 3 раза больше, чем образующая второго. Чему равна площадь боковой поверхности первого конуса, если площадь боковой поверхности второго равна 22 см 2? Ответ: 33 В меню
№ 9 В-9 Радиус основания первого конуса в 2 раза меньше, чем радиус основания второго конуса, а образующая первого конуса в 3 раза больше, чем образующая второго. Чему равна площадь боковой поверхности первого конуса, если площадь боковой поверхности второго равна 22 см 2? Ответ: 33 В меню
 № 10 В-9 Радиус основания первого конуса в 3 раза меньше, чем радиус основания второго конуса, а образующая первого конуса в 2 раза больше, чем образующая второго. Чему равна площадь боковой поверхности первого конуса, если площадь боковой поверхности второго равна 18 см 2? Ответ: 12 В меню
№ 10 В-9 Радиус основания первого конуса в 3 раза меньше, чем радиус основания второго конуса, а образующая первого конуса в 2 раза больше, чем образующая второго. Чему равна площадь боковой поверхности первого конуса, если площадь боковой поверхности второго равна 18 см 2? Ответ: 12 В меню
 № 11 В-9 • Концы отрезка МN лежат на окружностях двух оснований цилиндра. Радиус основания цилиндра равен 10, длина отрезка МN равна 24, а угол между прямой MN и плоскостью основания цилиндра равен 600. Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки М и N. Решение: O 1 M K O N Н Ответ: 8 В меню
№ 11 В-9 • Концы отрезка МN лежат на окружностях двух оснований цилиндра. Радиус основания цилиндра равен 10, длина отрезка МN равна 24, а угол между прямой MN и плоскостью основания цилиндра равен 600. Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки М и N. Решение: O 1 M K O N Н Ответ: 8 В меню
 Задания части С • • № 12 № 13 № 14 № 19, 20 (для самост. реш. ) • Объем • № 15, 16 (для самост. реш. ) • № 17, 18 (для самост. реш. ) В главное меню
Задания части С • • № 12 № 13 № 14 № 19, 20 (для самост. реш. ) • Объем • № 15, 16 (для самост. реш. ) • № 17, 18 (для самост. реш. ) В главное меню
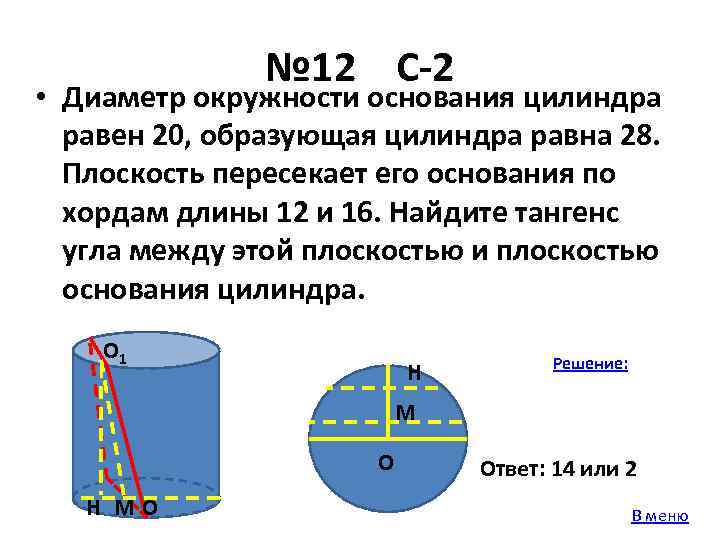 № 12 С-2 • Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. О 1 Н Решение: М О Н МО Ответ: 14 или 2 В меню
№ 12 С-2 • Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. О 1 Н Решение: М О Н МО Ответ: 14 или 2 В меню
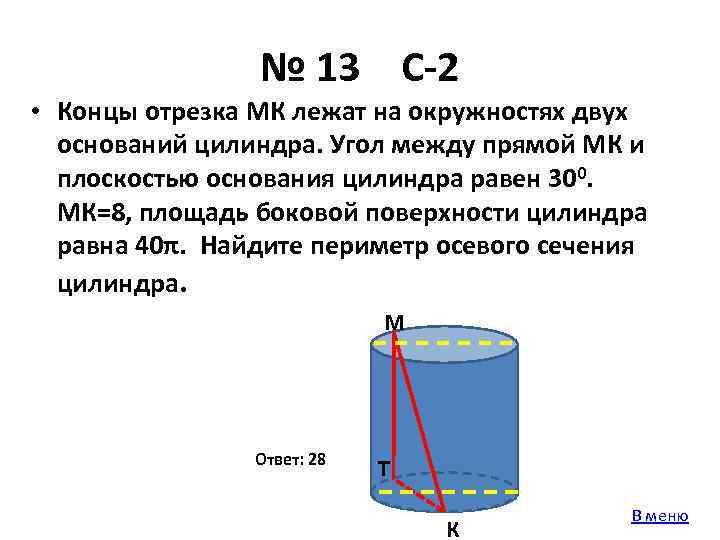 № 13 С-2 • Концы отрезка МК лежат на окружностях двух оснований цилиндра. Угол между прямой МК и плоскостью основания цилиндра равен 300. МК=8, площадь боковой поверхности цилиндра равна 40π. Найдите периметр осевого сечения цилиндра. М Ответ: 28 Т К В меню
№ 13 С-2 • Концы отрезка МК лежат на окружностях двух оснований цилиндра. Угол между прямой МК и плоскостью основания цилиндра равен 300. МК=8, площадь боковой поверхности цилиндра равна 40π. Найдите периметр осевого сечения цилиндра. М Ответ: 28 Т К В меню
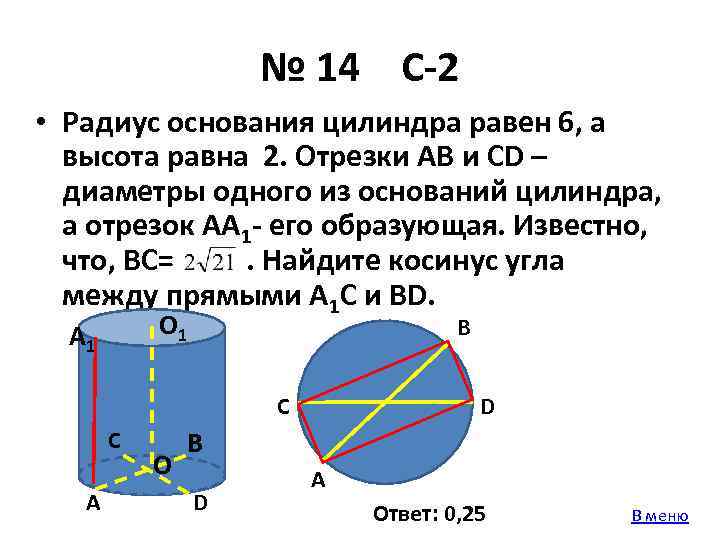 № 14 С-2 • Радиус основания цилиндра равен 6, а высота равна 2. Отрезки АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА 1 - его образующая. Известно, что, ВС=. Найдите косинус угла между прямыми А 1 С и ВD. О 1 А 1 В С С А О D В D А Ответ: 0, 25 В меню
№ 14 С-2 • Радиус основания цилиндра равен 6, а высота равна 2. Отрезки АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА 1 - его образующая. Известно, что, ВС=. Найдите косинус угла между прямыми А 1 С и ВD. О 1 А 1 В С С А О D В D А Ответ: 0, 25 В меню
 Задачи для самостоятельного решения № 15 С-2 № 16 С-2 • Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. • Диаметр окружности основания цилиндра равен 10, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. Ответ: 3 или 21/17 Ответ: 21 или 3 В меню
Задачи для самостоятельного решения № 15 С-2 № 16 С-2 • Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. • Диаметр окружности основания цилиндра равен 10, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. Ответ: 3 или 21/17 Ответ: 21 или 3 В меню
 Задачи для самостоятельного решения № 17 С -2 • Точки К и М лежат на • окружностях двух оснований цилиндра. Синус угла наклона прямой КМ к плоскости ВD основания цилиндра равен 0, 6, КМ=10, объем цилиндра равен 150π. Найдите площадь осевого сечения цилиндра. Ответ: 60 № 18 С -2 Точки В и D лежат на окружностях двух оснований цилиндра. Синус угла между прямой ВD и плоскостью основания цилиндра равен 0, 3, ВD =15, объем цилиндра равен 450π. Найдите площадь осевого сечения цилиндра. Ответ: 90 В меню
Задачи для самостоятельного решения № 17 С -2 • Точки К и М лежат на • окружностях двух оснований цилиндра. Синус угла наклона прямой КМ к плоскости ВD основания цилиндра равен 0, 6, КМ=10, объем цилиндра равен 150π. Найдите площадь осевого сечения цилиндра. Ответ: 60 № 18 С -2 Точки В и D лежат на окружностях двух оснований цилиндра. Синус угла между прямой ВD и плоскостью основания цилиндра равен 0, 3, ВD =15, объем цилиндра равен 450π. Найдите площадь осевого сечения цилиндра. Ответ: 90 В меню
 Задачи для самостоятельного решения № 19 С -2 № 20 С -2 • Радиус основания цилиндра равен 1, а высота равна Отрезки АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА 1 - его образующая. Известно, что, АD=. Найдите косинус угла между прямыми А 1 С и ВD. • Радиус основания цилиндра равен 5, а высота равна 6 Отрезки АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА 1 - его образующая. Известно, что, АD=. Найдите косинус угла между прямыми А 1 С и ВD. Ответ: 0, 2 Ответ: 0, 75 В меню
Задачи для самостоятельного решения № 19 С -2 № 20 С -2 • Радиус основания цилиндра равен 1, а высота равна Отрезки АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА 1 - его образующая. Известно, что, АD=. Найдите косинус угла между прямыми А 1 С и ВD. • Радиус основания цилиндра равен 5, а высота равна 6 Отрезки АВ и СD – диаметры одного из оснований цилиндра, а отрезок АА 1 - его образующая. Известно, что, АD=. Найдите косинус угла между прямыми А 1 С и ВD. Ответ: 0, 2 Ответ: 0, 75 В меню
 № 3 В-9 • Хорда основания цилиндра стягивает дугу в 600. Секущая плоскость содержит эту хорду и параллельна высоте цилиндра. Площадь сечения равна 20. Вычислите площадь боковой поверхности цилиндра. О 1 А О В Решение: Так как хорда стягивает дугу в 600, то ее длина равна радиусу. Значит, площадь сечения равна RH=20. Тогда площадь боковой поверхности равна 2πRH= 2π∙ 20= 40π Ответ: 40π В меню
№ 3 В-9 • Хорда основания цилиндра стягивает дугу в 600. Секущая плоскость содержит эту хорду и параллельна высоте цилиндра. Площадь сечения равна 20. Вычислите площадь боковой поверхности цилиндра. О 1 А О В Решение: Так как хорда стягивает дугу в 600, то ее длина равна радиусу. Значит, площадь сечения равна RH=20. Тогда площадь боковой поверхности равна 2πRH= 2π∙ 20= 40π Ответ: 40π В меню
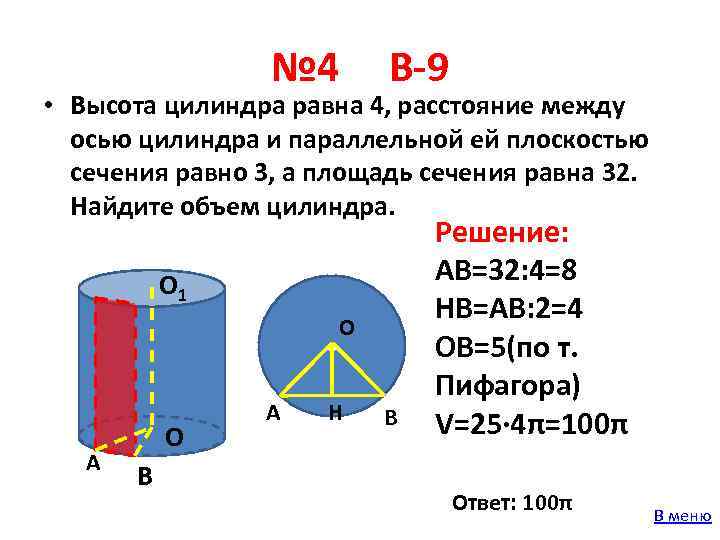 № 4 В-9 • Высота цилиндра равна 4, расстояние между осью цилиндра и параллельной ей плоскостью сечения равно 3, а площадь сечения равна 32. Найдите объем цилиндра. О 1 о А О В А О Н В Решение: АВ=32: 4=8 НВ=АВ: 2=4 ОВ=5(по т. Пифагора) V=25∙ 4π=100π Ответ: 100π В меню
№ 4 В-9 • Высота цилиндра равна 4, расстояние между осью цилиндра и параллельной ей плоскостью сечения равно 3, а площадь сечения равна 32. Найдите объем цилиндра. О 1 о А О В А О Н В Решение: АВ=32: 4=8 НВ=АВ: 2=4 ОВ=5(по т. Пифагора) V=25∙ 4π=100π Ответ: 100π В меню
 № 11 В-9 • Концы отрезка МN лежат на окружностях двух оснований цилиндра. Радиус основания цилиндра равен 10, длина отрезка МN равна 24, а угол между прямой MN и плоскостью основания цилиндра равен 600. Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки М и N. Решение: O 1 M K O N Н Ответ: 8 В меню
№ 11 В-9 • Концы отрезка МN лежат на окружностях двух оснований цилиндра. Радиус основания цилиндра равен 10, длина отрезка МN равна 24, а угол между прямой MN и плоскостью основания цилиндра равен 600. Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки М и N. Решение: O 1 M K O N Н Ответ: 8 В меню
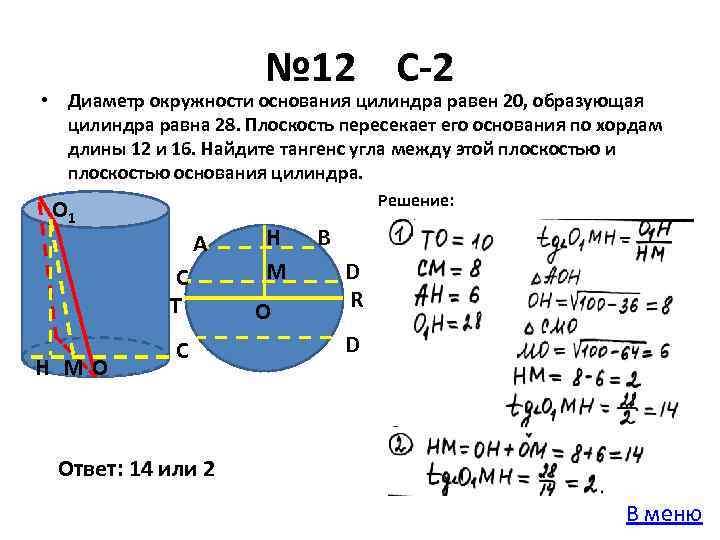 № 12 С-2 • Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. Решение: О 1 А С T Н МО С Н М О В D R D Ответ: 14 или 2 В меню
№ 12 С-2 • Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. Решение: О 1 А С T Н МО С Н М О В D R D Ответ: 14 или 2 В меню
 Литература 1. 2. 3. 4. 5. Атанасян Л. С. , Бутузов В. Ф. , Кадомцев С. Б. Геометрия. 10 -11 класс. Базовый и профильный уровень. М. , «Просвещение» , 2008. Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/ авт. - сост. И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров и др. ; под ред. А. Л. Семенова, И. В. Ященко. – М. : АСТ: Астрель, 2009. – (ФИПИ) ЕГЭ 2010. Математика: сборник заданий/ В. В. Кочагин , М. Н. Кочагина. – М. -Эксмо, 2009. ЕГЭ 2010. Математика. Типовые тестовые задания/ под ред. А. Л. Семенова, И. В. Ященко. – М. : Издательство «Экзамен» , 2010. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие/ Л. Д. Лаппо, М. А. Попов. - М. : Издательство «Экзамен» , 2010.
Литература 1. 2. 3. 4. 5. Атанасян Л. С. , Бутузов В. Ф. , Кадомцев С. Б. Геометрия. 10 -11 класс. Базовый и профильный уровень. М. , «Просвещение» , 2008. Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/ авт. - сост. И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров и др. ; под ред. А. Л. Семенова, И. В. Ященко. – М. : АСТ: Астрель, 2009. – (ФИПИ) ЕГЭ 2010. Математика: сборник заданий/ В. В. Кочагин , М. Н. Кочагина. – М. -Эксмо, 2009. ЕГЭ 2010. Математика. Типовые тестовые задания/ под ред. А. Л. Семенова, И. В. Ященко. – М. : Издательство «Экзамен» , 2010. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие/ Л. Д. Лаппо, М. А. Попов. - М. : Издательство «Экзамен» , 2010.


