ЗАДАЧА ПОТРЕБИТЕЛЬСКОГО ВЫБОРА ФУНКЦИЯ ПОЛЕЗНОСТИ КРИВЫЕ БЕЗРАЗЛИЧИЯ НОРМА

ЗАДАЧА ПОТРЕБИТЕЛЬСКОГО ВЫБОРА ФУНКЦИЯ ПОЛЕЗНОСТИ. КРИВЫЕ БЕЗРАЗЛИЧИЯ. НОРМА ЗАМЕНЫ И ПРЕДЕЛЬНАЯ НОРМА ЗАМЕНЫ. МЕТОДЫ РЕШЕНИЯ ЗАДАЧИПОТРЕБИТЕЛЬСКОГО ВЫБОРА. КРИВЫЕ «ДОХОД-ПОТРЕБЛЕНИЕ» И «ЦЕНАПОТРЕБЛЕНИЕ» ЛЕКЦИЯ

Рассмотрим некоторые модели поведения потребителей, называемые моделями потребительского выбора. В их основе лежит гипотеза о том, что каждый потребитель, осуществляя выбор наборов благ (продуктов) при заданных ценах на блага (продукты) и имеющемся у потребителя доходе, стремится максимизировать уровень удовлетворения своих И потребностей.

Постановка задачи. . Пусть индивидуальному потребителю предлагается два вида различных благ. Обозначим: – количество единиц первого блага, – количество единиц второго блага. Очевидно, и Потребительский набор благ можно математически описать двумерным вектором О п р е д е л е н и е 1. Вектор называется вектором благ. Обозначим рыночные цены блага и соответственно . Очевидно,

Тогда стоимость набора благ определяется вектором цен благ и вычисляется по формуле: (1) скалярное произведение векторов и . Стоимость любого блага, которое приобретает потребитель, не превосходит его дохода . Следовательно, должно выполняться линейное неравенство: (2)

О п р е д е л е н и е 3. Неравенство (2) называется бюджетным ограничением потребителя. Прямая называется бюджетной линией. О п р е д е л е н и е 4. Множеством доступных для потребителя наборовблаг на рынке товаров и услуг называется множество на плоскости обозначаемое К, решений неравенства (2), удовлетворяющих ограничениям (1). В зависимости от расположения на плоскости прямой возможны следующие три варианта.

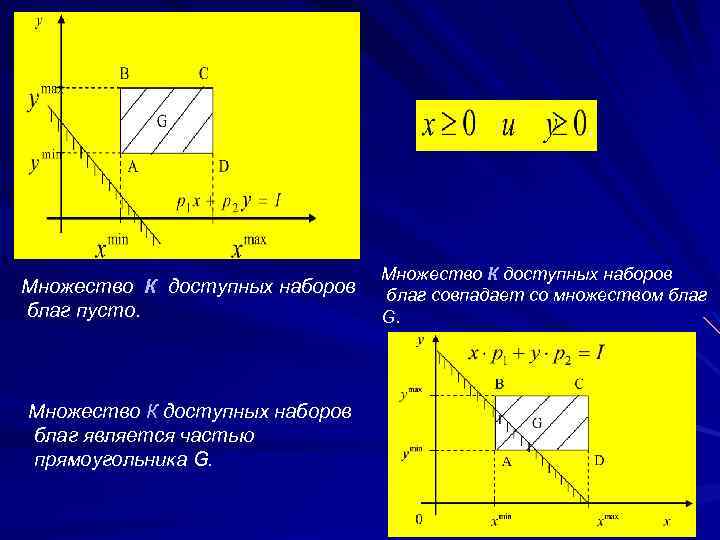
Множество К доступных наборов благ пусто. Множество К доступных наборов благ является частью прямоугольника G. Множество К доступных наборов благ совпадает со множеством благ G.

ФУНКЦИЯ ПОЛЕЗНОСТИ О п р е д е л е н и е 5. Полезностью блага называется способность блага удовлетворять ту или иную потребность покупателя. Потребитель при анализе двух наборов благ и выносит одно из суждений об их полезности: v набор благ предпочтительнее (полезнее), чем набор благ . Условно обозн. . vнаборы благ и одинаково предпочтительны для потребителя. Условно обозначается .

О п р е д е л е н и е 6. Функция называется функцией полезности блага для потребителя, если ее значение на потребительском наборе благ равно потребительской оценке индивидуума для этого набора. О п р е д е л е н и е 7. Потребительская оценка набора благ называется уровнем (или степенью) удовлетворения потребностей индивидуума, если он приобретает или потребляет данный набор благ . Функция полезности представляет, по существу, систему предпочтений потребителя.

Потребитель при выборе набора благ стремится максимизировать свою функцию полезности . Основные свойства функции полезности § Возрастание потребления одного продукта при постоянном потреблении второго приводит к росту потребления оценки: Первые частные производные от функции полезности потребителя называются предельными полезностями

§ Предельная полезность продукта уменьшается, если объем его потребления растет: Это свойство называется законом убывания предельной полезности или первым законом Госсена. Предельная полезность продукта увеличивается, если растет количество другого продукта: Это свойство справедливо не для всех товаров. Если товары полностью будут замещать друга, то это свойство не выполняется.

Одним из первых высказал идеи, вошедшие составной частью в теорию предельной полезности, немецкий экономист Г. Госсен. Его именем названы два закона; в чем их существо? Первый закон Германа Генриха Госсена (1810– 1859) – закон на сыщения потребностей. Он гласит: с удовлетворением потребности в каком либо благе его ценность падает или по мере увеличения количества товара его полезность убывает. Переход к насыщению потребности происходит обычно не сразу, а постепенно, как бы по ступеням.

Второй закон Госсена: упрощённый вариант основан на рассмотрении натурального хозяйства человека, изолированного от общества. При наличии определённого количества различных продуктов индивидуум в течение данного ограниченного периода времени может потребить их в разных комбинациях, одна из которых должна быть наиболее выгодной, приносящей максимум наслаждения. Это достигается при установлении равенства предельных полезностей всех продуктов.

Следующая степень приближения учитывает условия товарного хозяйства. Цена товаров и количество денег — главные факторы, ограничивающие потребление. Оптимальным будет тот вариант потребления, при котором достигается равенство между предельными полезностями, получающимися от последних денежных единиц, израсходованных на покупку отдельных товаров. Второй закон впоследствии широко использовался математической школой для объяснения явлений спроса и ценообразования.

§ Функция полезности дважды дифференцируема по каждому аргументу. § Имеет непрерывные частные производные. § График функции полезности вогнутый.

О п р е д е л е н и е 7. Линией безразличия функции называется линия на плоскости , соединяющая те потребительские наборы благ , которые имеют один и тот же уровень удовлетворения потребностей индивидуума. Другими словами линия безразличия состоит из тех точек множества доступных для потребителя благ К, которые равноценны, одинаково предпочтительны потребителю, что ему безразлично, какой из этих наборов благ выбрать.

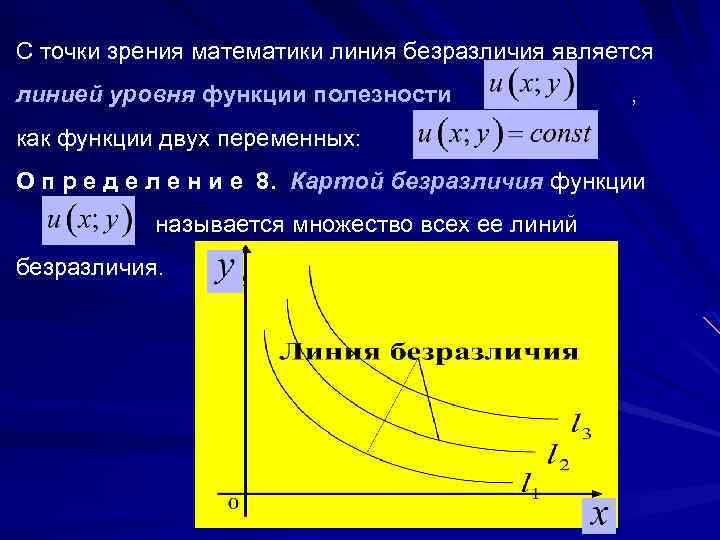
С точки зрения математики линия безразличия является линией уровня функции полезности , как функции двух переменных: О п р е д е л е н и е 8. Картой безразличия функции называется множество всех ее линий безразличия.

ЗАДАЧА ОПТИМАЛЬНОГО ВЫБОРА БЛАГ Задача оптимального выбора благ потребителем заключается в выборе такого набора благ который максимизирует его функцию полезности при заданном бюджетном ограничении где – доход потребителя, который он готов потратить на приобретение первого и второго продуктов. Величины I, , - заданы.

Математически задача оптимального выбора благ имеет вид: (1) при условиях (2) (3) Задачу (1) (3) называют задачей потребительского выбора.

Прямая АВ соответствует бюджетному ограничению, треугольник АОВ – область доступных наборов, а точка – точка касания кривой безразличия со стороной АВ треугольника АОВ, которая и определяет оптимальный набор благ задачи (1)-(3).

Т е о р е м а 1. Задача (1), (2), (3) оптимального выбора благ потребителем имеет решение и притом только одно. Оптимальное решение задачи (1) (3) называется точкой равновесия задачи оптимального выбора благ потребителем. В приведенной постановке задача (1) (3) оптимального выбора благ потребителем является задачей нелинейного программирования.

Задачу (1) (3) выбора благ потребителем можно заменить задачей на условный экстремум: (4) при условиях (5) (6) Для решения задачи (4), (5), (6) на условный экстремум применим метод Лагранжа. Для этого составим функцию Лагранжа по формуле:

Составим систему уравнений: ЛАГРАНЖ Жозеф Луи (Lagrange Joseph-Louis) 25. 01. 1736 -10. 04. 1813 -

системы является критической Решение точкой функции Лагранжа. Более того, подставляя решение в первое уравнение системы, получаем: Геометрически решение можно интерпретировать как точку касания линии безразличия, построенной для функции полезности , с бюджетной линией .

и. Координаты и оптимального решения задачи (1)-(3) оптимального выбора благ потребителем представляют собой функцию параметров.

. З а д а ч а. Функция полезности задана формулой: При ценах благ а) решить задачу оптимального выбора благ, б) найти функции спроса, в) изобразить на плоскости множеством доступных для потребителя благ и кривые безразличия. Р е ш е н и е. Запишем задачу потребительского выбора в следующем виде:

а) Бюджетная линия в данной задаче задается уравнением Задача является классической задачей на условный экстремум: Составим функцию Лагранжа:

б) Учитывая формулы значения цен благ и доход уравнение бюджетной линии находим функции спроса задачи: Итак, расходы потребителя на каждое благо составляют половину его общего дохода. в) Множество доступных для потребителя наборов благ и кривые безразличия рассматриваемой задачи изображены на сл. рис.

О т в е т:

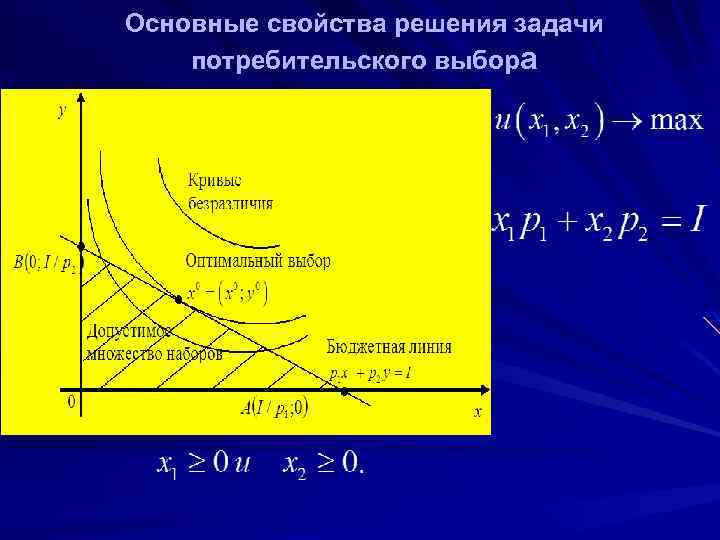
Основные свойства решения задачи потребительского выбора

1. Решение задачи не изменяется при любом монотонном преобразовании функции полезности и неизменном бюджетном ограничении. Монотонным преобразованием функции полезности может быть ее умножение на некоторое положительное число, возведение ее в положительную степень, логарифмирование по основанию, большему единицы. При монотонном преобразовании функции полезности ее первые частные производные остаются положительными. Но свойства вторых частных производных могут теряться или приобретаться.

2. Решение задачи потребительского выбора не изменяется, если все цены и доход увеличатся (уменьшатся) в одно и тоже число раз. Действительно, умножение на положительное число правой и левой частей бюджетного ограничения делает его эквивалентным исходному.

Задача. Функция полезности для двух товаров имеет вид: Бюджетное ограничение и цены на первый товар и второй товар связаны соотношением . Определите функцию спроса на товары. Решение. Задача потребительского выбора имеет следующий вид:

Функция Лагранжа для этой задачи имеет вид: Приравниваем к нулю первые частные производные функции Лагранжа:

Подставляя в выражение , получим

Кривые «доход-потребление» Из уравнения получим: Бюджетная прямая и линия безразличия в оптимальной точке касаются друга. Если доход изменяется при постоянстве цен на товары, то бюджетная прямая сдвигается параллельно самой себе, так как тангенс угла наклона не меняется.

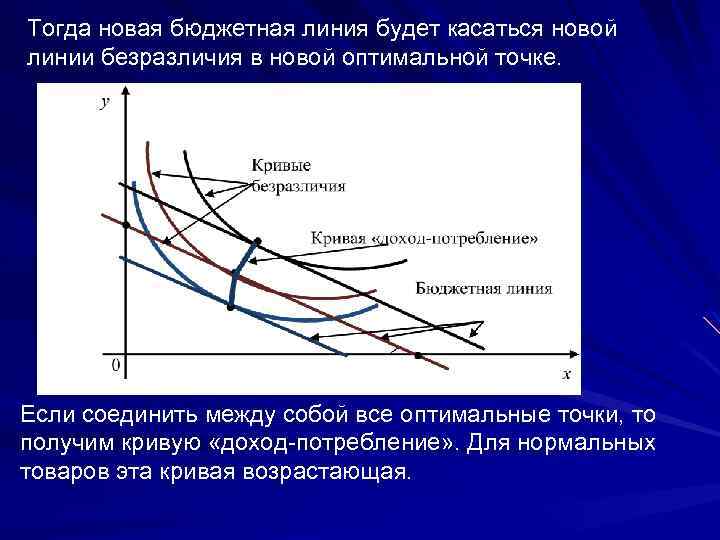
Тогда новая бюджетная линия будет касаться новой линии безразличия в новой оптимальной точке. Если соединить между собой все оптимальные точки, то получим кривую «доход потребление» . Для нормальных товаров эта кривая возрастающая.

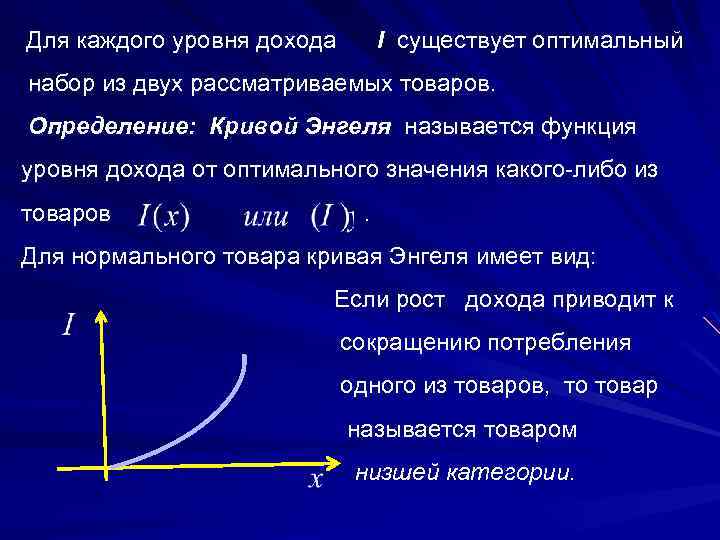
Для каждого уровня дохода I существует оптимальный набор из двух рассматриваемых товаров. Определение: Кривой Энгеля называется функция уровня дохода от оптимального значения какого либо из товаров . Для нормального товара кривая Энгеля имеет вид: Если рост дохода приводит к сокращению потребления одного из товаров, то товар называется товаром низшей категории.

Задача потребительского выбора для произвольного числа товаров Для произвольного числа товаров задача потребительского выбора формулируется сл. образом: при условиях где функция полезности; бюджетное ограничение; цены на I, II и. т. д. товары; количество приобретённых товаров I, II и. т. д. типов.

Задачу нелинейного программирования можно заменить задачей на условный экстремум: Функция Лагранжа имеет вид Приравниваем к нулю первые частные производные функции Лагранжа:

Умножим уравнение под номером I на , а уравнение под номером j на и вычтем одно из другого. Получим: Таким образом, в точке оптимума отношение предельных полезностей любых двух товаров равно отношению их рыночных цен.

Модель Р. Стоуна Пусть функция полезности имеет следующий вид: Бюджетное ограничение и цены на товары связаны соотношением где номер товара; минимальное необходимое количество го товара, которое приобретается в любом случае; показатель относительной ценности товара для потребителя. Определить функции спроса на товар.

Ричард Стоун родился в 1913 г. в Лондоне. Лауреат нобелевской премии 1984 года «за новаторскую работу в области создания системы национальных счетов» , доктор физико математических наук (D. Sc. ) родного университета; профессор Кембриджского университета, президент Экономического общества (1955). Умер в 1991 году.

Решение. Данную задачу нелинейного программирования можно заменить задачей на условный экстремум: при условиях Функция Лагранжа имеет сл. вид:

Для любого слагаемого из уравнения (1) можно записать

Умножив полученное уравнение на и просуммируем их по j от 1 до n , получим

Учитывая , что из выражения находим: Последнее подставляем в выражение

Получим: Из полученного следует, что спрос на j - й товар равен минимально необходимому количеству j - ого товара плюс количество, пропорциональное показателю относительной ценности этого товара для потребителя.

Кривые «доход-потребление» Из уравнения получим: Т. е. бюджетная прямая и линия безразличия в оптимальной точке касаются друга. Если доход изменяется при постоянстве цен на товары, то бюджетная прямая сдвигается параллельно самой себе, так как тангенс угла наклона не меняется.

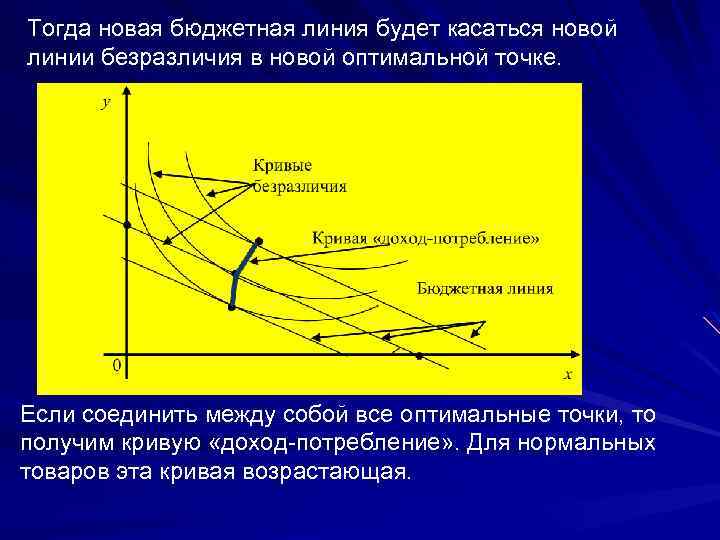
Тогда новая бюджетная линия будет касаться новой линии безразличия в новой оптимальной точке. Если соединить между собой все оптимальные точки, то получим кривую «доход потребление» . Для нормальных товаров эта кривая возрастающая.

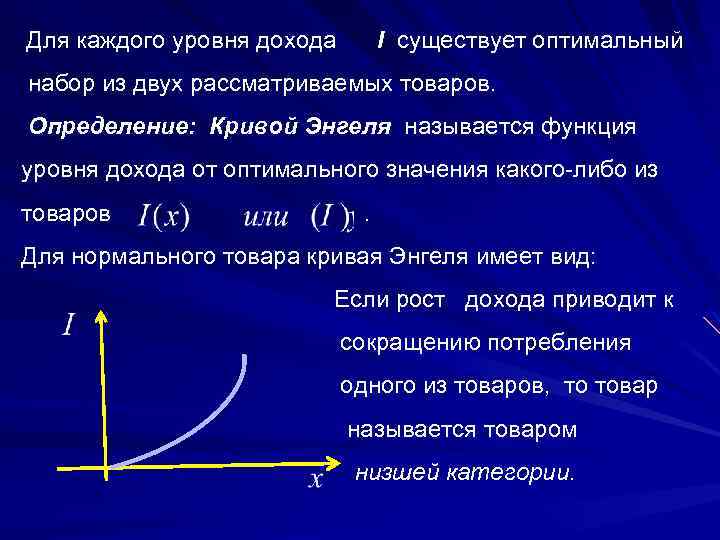
Для каждого уровня дохода I существует оптимальный набор из двух рассматриваемых товаров. Определение: Кривой Энгеля называется функция уровня дохода от оптимального значения какого либо из товаров . Для нормального товара кривая Энгеля имеет вид: Если рост дохода приводит к сокращению потребления одного из товаров, то товар называется товаром низшей категории.