Лекция ММ 4.pptx
- Количество слайдов: 15

Задача оценки математических моделей - это задача выбора, для решения которой необходимо определить функцию эффективности. Эффективность модели - это Эта функция должна её приспособленность к достигать экстремальных достижению цели. значений при выборе Чтобы иметь возможность судить модели наиболее об эффективности модели, необходим численный критерий подходящей для оценки или показатель достижения целей эффективности. Этот критерий моделирования с учётом принято обозначать W. Явный вид возможных материальных показателя эффективности и временных ограничений. определяется исходя из целей и конкретных условий моделирования.

Среди множества вариантов моделирования лучшим считается тот, который доставляет показателю эффективности экстремальное значение. Кроме этого функция эффективности должна характеризовать всю модель и её значения должны быть вычислимы по возможности наиболее простым способом. Предположим, что имеется математическая модель, позволяющая оценить значение W при любом принятом решении, для любой совокупности условий. Обозначим αi, (i = 1, 2, . . )- известные факторы, на которые мы влиять не можем; xj, (j = 1, 2, . . . ) - факторы, которые мы можем выбирать по своему усмотрению. Показатель эффективности зависит от всех этих факторов, т. е. W = W(α , x ) i j Задача поиска функции эффективности формулируется следующим образом: "При заданных условиях αt найти такие элементы решения xj, при которых показатель эффективности W достигает экстремума".

В рассматриваемом случае задача сводится к отысканию экстремума функции W. Возникающие при этом возможные трудности имеют не принципиальный, а вычислительный характер. В действительности моделирование может осуществляться, когда не все условия известны заранее, некоторые из них содержат элемент неопределённости. Обозначим эти неизвестные условия или параметры Yk, (k = 1, 2, . . . ). Тогда, очевидно, W = W(αi, Yk, xj) Задача формулируется следующим образом: "При заданных условиях αt, с учётом неизвестных факторов Yk найти такие решения хj, при которых показатель эффективности W по возможности достигал бы экстремума".

Выбор решения в условиях неопределённости в значительной мере зависит от природы неопределённости. Неопределённость бывает разного происхождения: · неизвестность (есть ли жизнь на Марсе? ), · расплывчатость, · случайность (вид неопределённости, подчиняющийся строгой закономерности, которая выражается распределением вероятностей).

Наиболее простым и благоприятным для расчётов является случай, когда неизвестные факторы Yk есть случайные величины или случайные функции, о которых имеются статистические данные, характеризующие их распределение, т. е. они статистически устойчивы. В этом случае для нахождения оптимального решения или заменяют случайные факторы на неслучайные (чаще всего на их математические ожидания) и неопределённая, вероятностная картина явления приближённо заменяется детерминированной. Или применяют метод статистических испытаний (метод Монте-Карло), выбирая в качестве оптимального решения то, при котором достигает экстремума математическое ожидание показателя эффективности.

Эффективность больших и сложных моделей не может быть охарактеризована одним показателем эффективности и приходится использовать множество показателей. Пусть анализируется операция U, оцениваемая по двум показателям: W вероятность достижения цели и S - стоимость израсходованных средств. Первый показатель желательно обратить в максимум, а второй - в минимум, т. е. где x - вектор параметров (свойств), соответствующих тому или иному решению. Тогда каждому допустимому значению x соответствует точка на плоскости (W, S), которая при изменении x опишет в этой плоскости некоторую линию
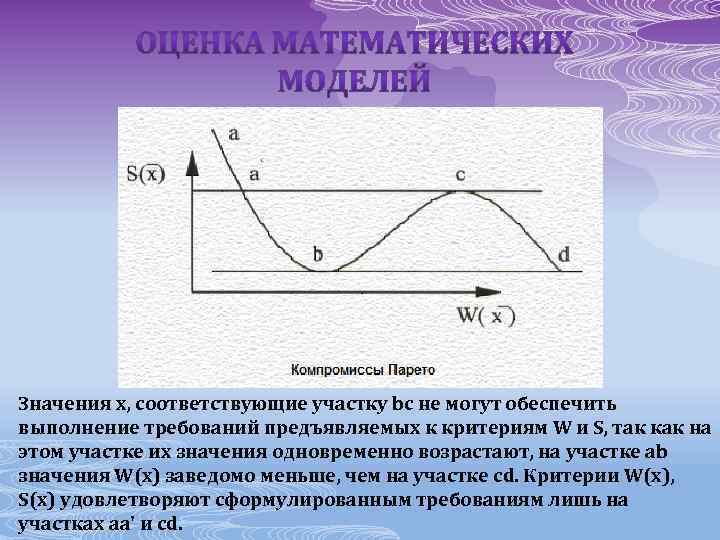
Значения x, соответствующие участку bс не могут обеспечить выполнение требований предъявляемых к критериям W и S, так как на этом участке их значения одновременно возрастают, на участке аb значения W(x) заведомо меньше, чем на участке cd. Критерии W(x), S(x) удовлетворяют сформулированным требованиям лишь на участках аа' и сd.

Таким образом имеется возможность уменьшить множество вариантов решения, исключив из рассмотрения заведомо худшие. Этот путь решения предложен итальянским экономистом В. Парето. Множество решений, полученных таким образом, называют множеством Парето. Выбор решения из множества Парето называют принципом Парето. Часто, чтобы избежать оценки операции по нескольким критериям, их объединяют в один обобщённый критерий. В. Парето

Эта процедура реализуется в зависимости от операции по-разному. 1. Обобщённый показатель представляется дробью в числителе дроби ставят те показатели, которые желательно увеличить, а в знаменателе - те, которые желательно уменьшить. 2. Обобщённый показатель представляется в виде взвешенной суммы отдельных показателей эффективности где ai - весовые коэффициенты, имеющие знак "+" при тех показателях, которые желательно увеличить, и знак "-" при тех, которые желательно уменьшить.

3. Из множества показателей эффективности выделяют один, наиболее важный и стремятся получить оптимальное решение лишь по этому единственному критерию. На остальные показатели эффективности накладывают ограничения вида: и включают в число заданных условий проведения операции

4. Показатели эффективности располагают в порядке убывающей важности. Для простоты будем считать, что каждый из них нужно обратить в максимум (если это не так, достаточно изменить знак показателя). Сначала ищется решение, обращающее показатель W 1 в максимум. Затем назначается, исходя из практических соображений и точности исходных данных, некоторая уступка ΔW 1, ценой которой можно добиться максимума показателя W 2, т. е. на W 1 накладывается ограничение: где W*1 - максимально возможное значение W 1, и при этом ограничении ищем решение, при котором достигается максимум показателя W 2. Этот процесс продолжается по мере необходимости. Этот метод поиска компромиссного решения хорош тем, что всегда известно, ценой какой уступки в одном показателе достигается выигрыш в другом.

Экономичность математической модели Экономичность (Э) модели оценивается разностью между ценностью (S) новой информации, полученной с помощью модели, и затратами (Z) на получение новой информации. Э=S-Z Под новой информацией понимаются неизвестные ранее сведения, пополняющие знания, уточняющие предположения и гипотезы. Ценность новой информации зависит от точности, своевременности, полноты, соответствия целям моделирования, возможности восприятия.

Экономичность математической модели Затраты на получение новой информации складываются из стоимости разработки и эксплуатации модели. Многие модели полностью или частично могут быть использованы при создании других моделей. Это свойство моделей называют универсальностью моделей. Очевидно, что универсальность модели снижает затраты на её создание и повышает экономичность. Однако, следствием универсальности является усложнение модели, необходимость учёта многочисленных, в конкретных условиях второстепенных, свойств объекта и затруднения при её использовании. Попытка создать универсальную модель для решения разнообразных задач настолько может усложнить модель, что она становится непригодной для применения. Опыт показал, что лучше для каждого объекта строить свою модель, в которой отображаются наиболее важные, существенные в данном иисследовании свойства объекта.

Адекватность математической модели и объекта - это правильность отображения в модели свойств объекта в той мере, которая необходима для достижения цели моделирования. Существует несколько аспектов оценки адекватности модели и объекта: 1. Математическая основа модели должна быть непротиворечивой, подчиняться всем законам математической логики. 2. Математическая модель должна правильно отображать исходный объект и обеспечивать возможность предсказывать изменения состояния объекта. Для этого в модели должны выполняться законы сохранения, присущие объекту моделирования. 3. При анализе результатов моделирования, их интерпретации необходимо использовать не только формальные методы, но и, так называемые, неформальные процедуры, основанные на опыте и интуиции человека.

Адекватность математической модели и объекта Таким образом, оценка адекватности математической модели и объекта выполняется на различных этапах математического моделирования: • при постановке задачи, в процессе построения модели, • при анализе и интерпретации результатов, вследствие чего эта процедура приобретает циклический характер. Стандартной методики проверки адекватности модели объекту не существует. В каждом конкретном случае разработчик формирует систему вопросов, в которых отражаются все аспекты оценки адекватности и ответы на которые позволяют сделать вывод об адекватности модели и объекта, т. е. ответить на вопрос: отражает ли модель заданные свойства объекта в соответствии с предъявляемыми требованиями, необходимыми для достижения целей моделирования.
Лекция ММ 4.pptx