Задача нахождения кратчайшего пути Данная задача состоит в

Задача нахождения кратчайшего пути Данная задача состоит в определении в транспортной сети кратчайшего пути между заданными исходным пунктом и пунктом назначения. Такую модель можно использовать для описания разнообразных ситуаций, как показано в следующем разделе.

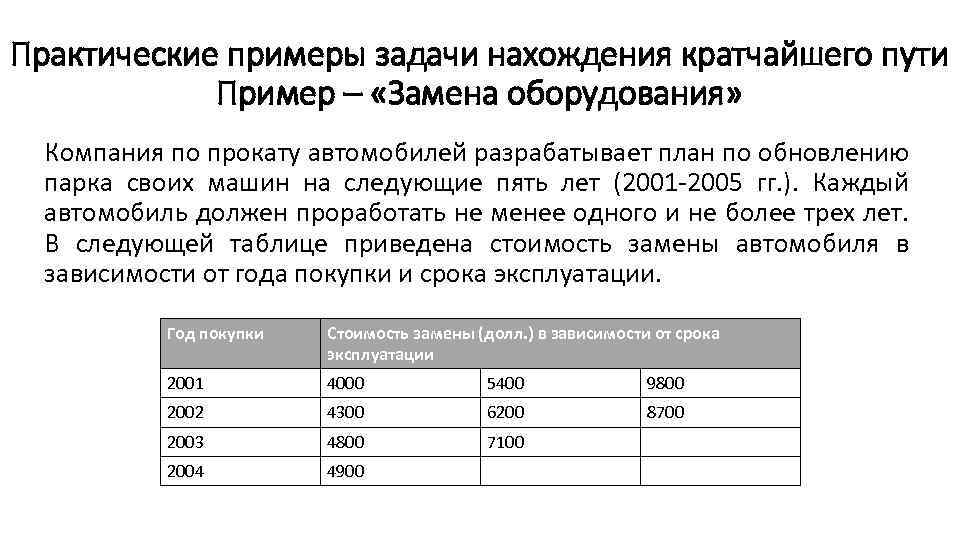Практические примеры задачи нахождения кратчайшего пути Пример – «Замена оборудования» Компания по прокату автомобилей разрабатывает план по обновлению парка своих машин на следующие пять лет (2001 -2005 гг. ). Каждый автомобиль должен проработать не менее одного и не более трех лет. В следующей таблице приведена стоимость замены автомобиля в зависимости от года покупки и срока эксплуатации. Год покупки Стоимость замены (долл. ) в зависимости от срока эксплуатации 2001 4000 5400 9800 2002 4300 6200 8700 2003 4800 7100 2004 4900

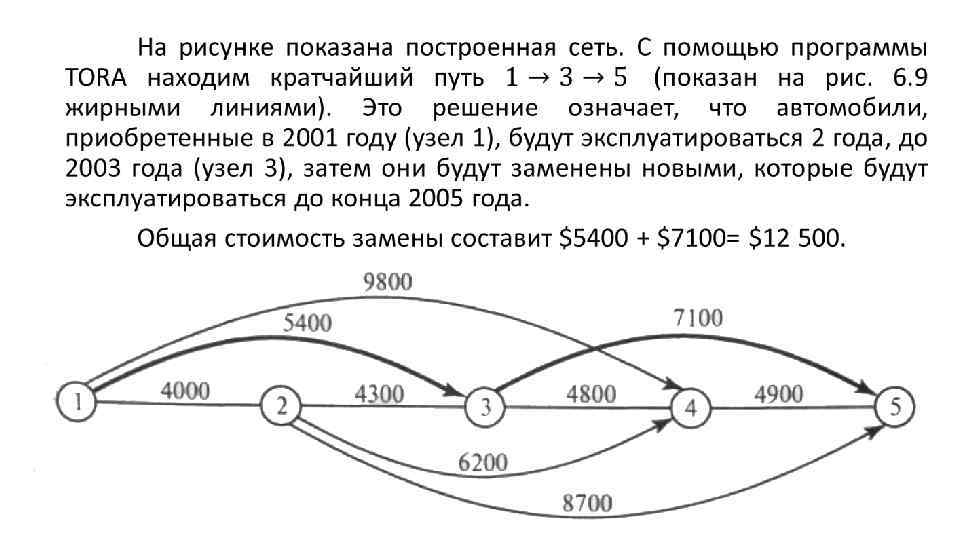
Формулировка задачи Задачу можно сформулировать как сетевую с пятью узлами с номерами от 1 до 5, соответствующими годам 2001 -2005. Из узла 1 (2001 год) дуги идут только к узлам 2, 3 и 4, поскольку автомобиль может эксплуатироваться не менее одного и не более трех лет. Дуги из других узлов интерпретируются аналогично. Стоимости дуг равны стоимостям замены автомобилей. Решение задачи эквивалентно нахождению кратчайшего пути между узлами 1 и 5. Таким образом задача замены оборудования решается как задача поиска кратчайшего пути.

•

Пример – «Самый надежный маршрут» М-р Разумник ежедневно ездит на работу на автомобиле. Закончив в свое время полный курс по теории исследования операций, он легко определил самый короткий путь от дома до работы. К сожалению, данный маршрут усиленно патрулируется нарядами полиции, и автомобиль Разумника часто останавливают за превышение скорости (как ему кажется, не обоснованно). Таким образом, самый короткий путь оказался не самым быстрым. Поэтому м-р Разумник планирует разработать новый маршрут, на котором он имел бы самую высокую вероятность не быть остановленным полицией.

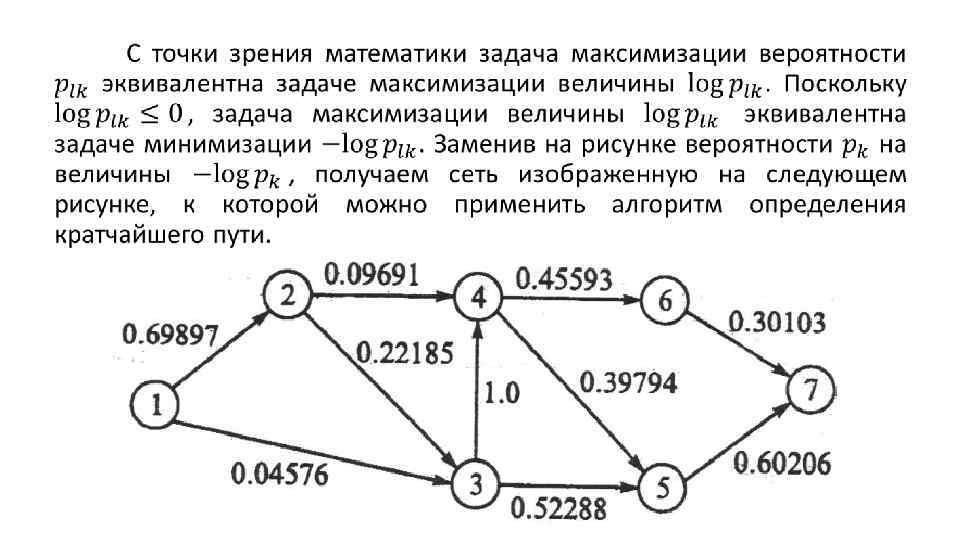
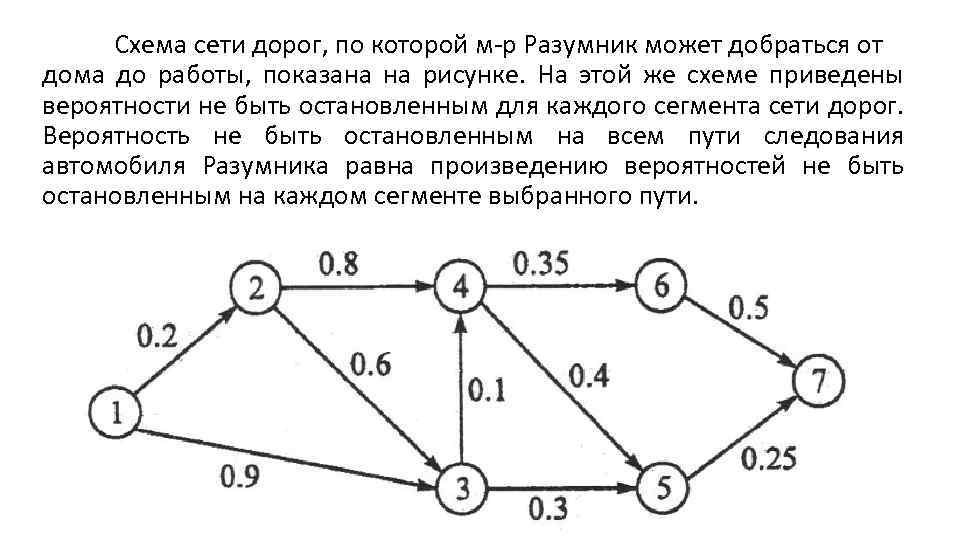Схема сети дорог, по которой м-р Разумник может добраться от дома до работы, показана на рисунке. На этой же схеме приведены вероятности не быть остановленным для каждого сегмента сети дорог. Вероятность не быть остановленным на всем пути следования автомобиля Разумника равна произведению вероятностей не быть остановленным на каждом сегменте выбранного пути.

•

•

•

Пример – «Головоломка о трех бидонах» Восьмилитровый бидон заполнен некой жидкостью, а два бидона емкостью 5 и 3 литра пусты. Необходимо разделить 8 литров жидкости на две равные части, используя только три имеющихся бидона. Какое минимальное количество переливаний из бидона в бидон надо сделать, чтобы достичь желаемого результата? Вы, вероятно, уже нашли решение этой головоломки. Вместе с тем ее можно решить как задачу о нахождении кратчайшего пути. В этой сетевой модели каждый узел будет соответствовать объемам жидкости в 8 -, 5 - и 3 -литровом бидонах. Начальным узлом будет (8, 0, 0), а конечным - (4, 4, 0). Новый узел получается из текущего при однократном переливании жидкости из одного бидона в другой.

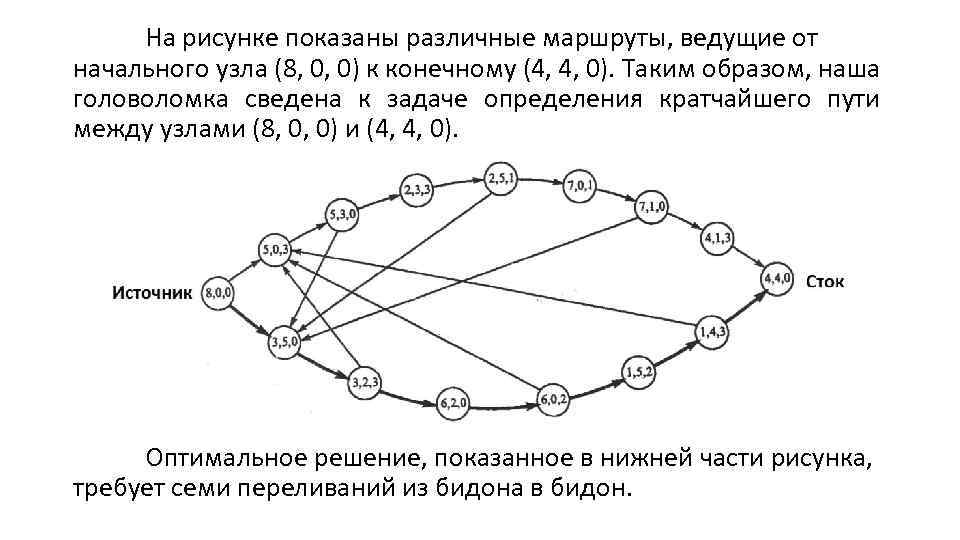На рисунке показаны различные маршруты, ведущие от начального узла (8, 0, 0) к конечному (4, 4, 0). Таким образом, наша головоломка сведена к задаче определения кратчайшего пути между узлами (8, 0, 0) и (4, 4, 0). Оптимальное решение, показанное в нижней части рисунка, требует семи переливаний из бидона в бидон.

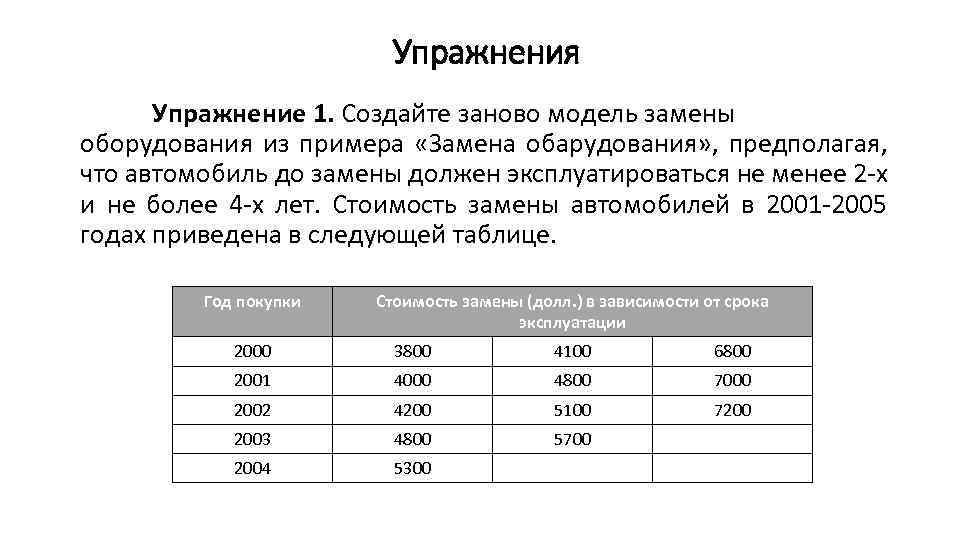Упражнения Упражнение 1. Создайте заново модель замены оборудования из примера «Замена обарудования» , предполагая, что автомобиль до замены должен эксплуатироваться не менее 2 -х и не более 4 -х лет. Стоимость замены автомобилей в 2001 -2005 годах приведена в следующей таблице. Год покупки Стоимость замены (долл. ) в зависимости от срока эксплуатации 2000 3800 4100 6800 2001 4000 4800 7000 2002 4200 5100 7200 2003 4800 5700 2004 5300

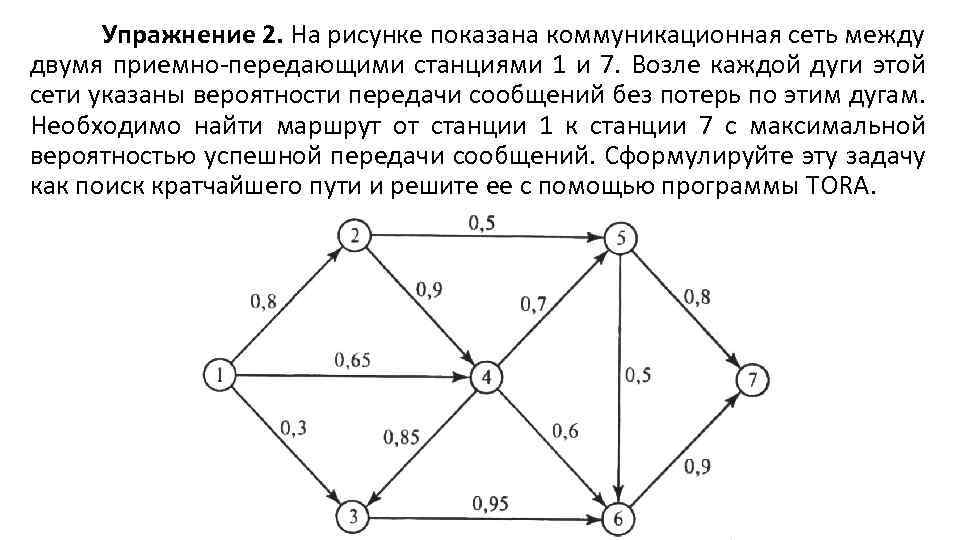Упражнение 2. На рисунке показана коммуникационная сеть между двумя приемно-передающими станциями 1 и 7. Возле каждой дуги этой сети указаны вероятности передачи сообщений без потерь по этим дугам. Необходимо найти маршрут от станции 1 к станции 7 с максимальной вероятностью успешной передачи сообщений. Сформулируйте эту задачу как поиск кратчайшего пути и решите ее с помощью программы TORA.

Упражнение 3. Тостер старой конструкции имеет две подпружиненные дверцы на петлях, размещенные с обеих сторон тостера. Ломтик хлеба помещается в тостер с одной стороны и дверца закрывается, затем другой ломтик хлеба загружается в тостер с противоположной стороны. После того как одна сторона ломтика хлеба подрумянится, он переворачивается. Задача заключается в определении последовательности операций (помещение ломтика хлеба, поджаривание одной стороны, переворачивание ломтика в тостере и извлечение готового хлеба из тостера), необходимых для поджаривания трех ломтиков хлеба за минимально возможное время. Сформулируйте эту задачу как определение кратчайшего пути, используя следующие данные о времени выполнения различных операций. Операция Время (секунды) Помещение ломтика хлеба в тостер 3 Поджаривание одной стороны ломтика 30 Переворачивание ломтика в тостере 1 Извлечение ломтика из тостера 3

Упражнение 4. «Планирование производства» . Компания продает некую продукцию, спрос на которую в следующие 4 месяца составит 100, 140, 210 и 180 единиц соответственно. Компания может удовлетворить любой помесячный спрос на продукцию и даже спрос на два и более месяцев вперед. В последнем случае необходимо платить $1, 20 за хранение единицы избыточно произведенной продукции в течение месяца. Покупная цена единицы продукции в следующие 4 месяца будет равна $15, $12, $10 и $14 соответственно. Стоимость переналадки оборудования для выполнения заказа составляет $200. Компания хочет разработать такой производственный план, чтобы минимизировать расходы на выполнение заказов, покупку продукции и ее хранение. Сформулируйте задачу как поиск кратчайшего пути и найдите ее оптимальное решение с помощью программы TORA.

Упражнение 5. «Задача о рюкзаке» . Путешественник, собираясь в путь, пытается поместить в свой рюкзак (объемом 5 кубических футов) наиболее необходимые в путешествии вещи. Есть три вещи, объемом соответственно 2, 3 и 4 кубических фута, необходимость в которых оценивается (по 100 -балльной шкале) в 30, 50 и 70 баллов. Сформулируйте эту задачу как сетевую, где необходимо определить самый длинный путь, и найдите ее оптимальное решение. (Совет: узел в этой сети можно определить как пару [i, и], где i номер выбираемой вещи, a v - свободный объем рюкзака, оставшийся после выбора t-й вещи).

Алгоритм нахождения кратчайшего пути В этом разделе представлены два алгоритма для решения задачи поиска кратчайшего пути как в сетях, имеющих циклы, так и в сетях, не имеющих циклов. 1. Алгоритм Дейкстры. 2. Алгоритм Флойда. Алгоритм Дейкстры разработан для поиска кратчайшего пути между заданным исходным узлом и любым другим узлом сети. Алгоритм Флойда более общий, поскольку он позволяет одновременно найти минимальные пути между любыми двумя узлами сети.

Алгоритм Дейкстры •

Шаги вычислительной схемы алгоритма Дейкстры •

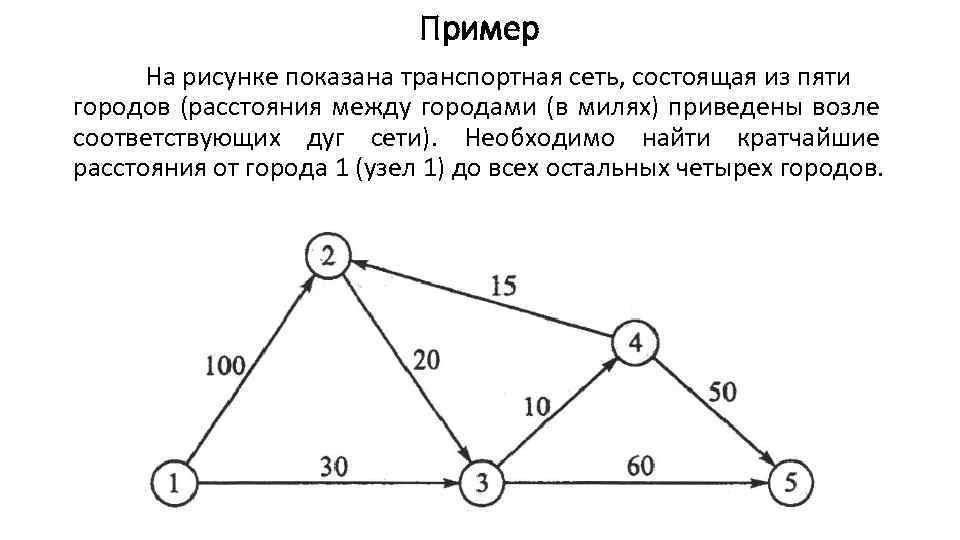Пример На рисунке показана транспортная сеть, состоящая из пяти городов (расстояния между городами (в милях) приведены возле соответствующих дуг сети). Необходимо найти кратчайшие расстояния от города 1 (узел 1) до всех остальных четырех городов.

Решение Шаг 0. Назначаем узлу 1 постоянную метку [0, -]. Шаг 1. Из узла 1 можно достичь узлов 2 и 3. Вычисляем метки для этих узлов, в результате получаем следующую таблицу меток: Узел Статус метки 1 [0, -] Постоянная 2 [0 + 100, 1] = [100, 1] Временная 3 Метка [0 + 30, 1] = [30, 1] Временная

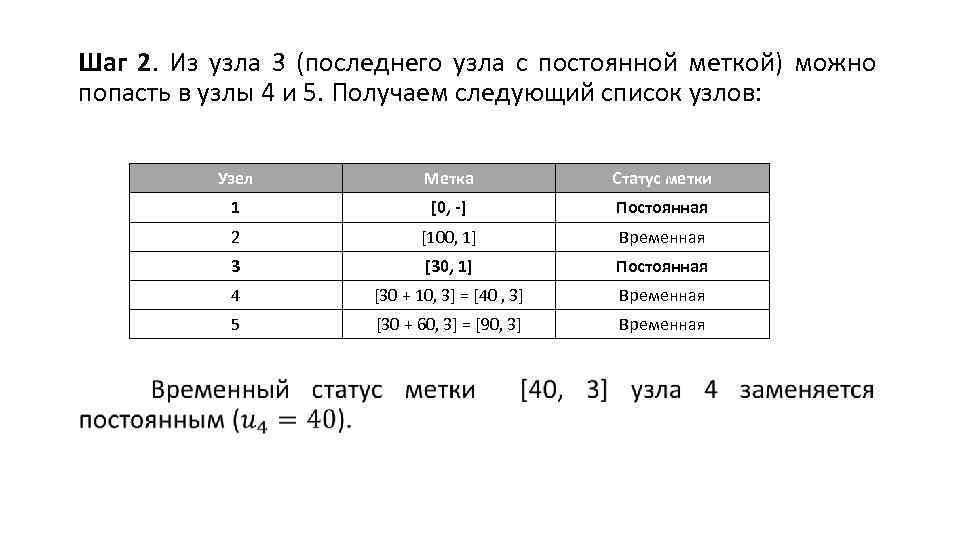Шаг 2. Из узла 3 (последнего узла с постоянной меткой) можно попасть в узлы 4 и 5. Получаем следующий список узлов: Узел Статус метки 1 [0, -] Постоянная 2 [100, 1] Временная 3 [30, 1] Постоянная 4 [30 + 10, 3] = [40 , 3] Временная 5 Метка [30 + 60, 3] = [90, 3] Временная

Шаг 3. Из узла 4 можно достичь узлов 2 и 5. После вычисления меток получим следующий их список: Узел Статус метки 1 [0, -] Постоянная 2 [40 + 15, 4] = [55, 4] Временная 3 [30, 1] Постоянная 4 [40 , 3] Постоянная 5 Метка [90, 3] или [40 + 50, 4] = [90, 4] Временная

Шаг 4. Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому на данном этапе получаем такой же список меток, как и на предыдущем, но с единственным изменением: метка узла 2 получает статус постоянной. С временной меткой остается только узел 5, но, так как из этого узла нельзя попасть ни в какой другой, процесс вычислений заканчивается.

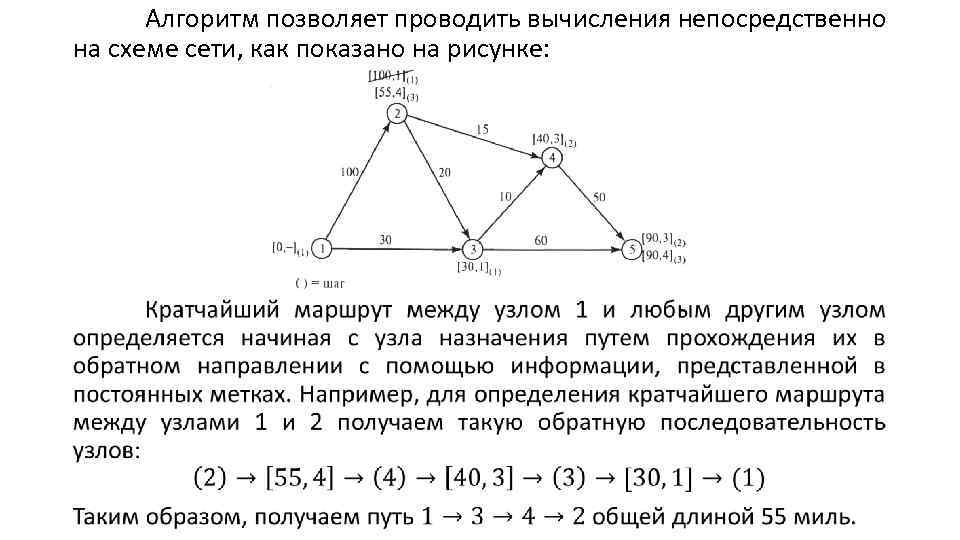Алгоритм позволяет проводить вычисления непосредственно на схеме сети, как показано на рисунке:

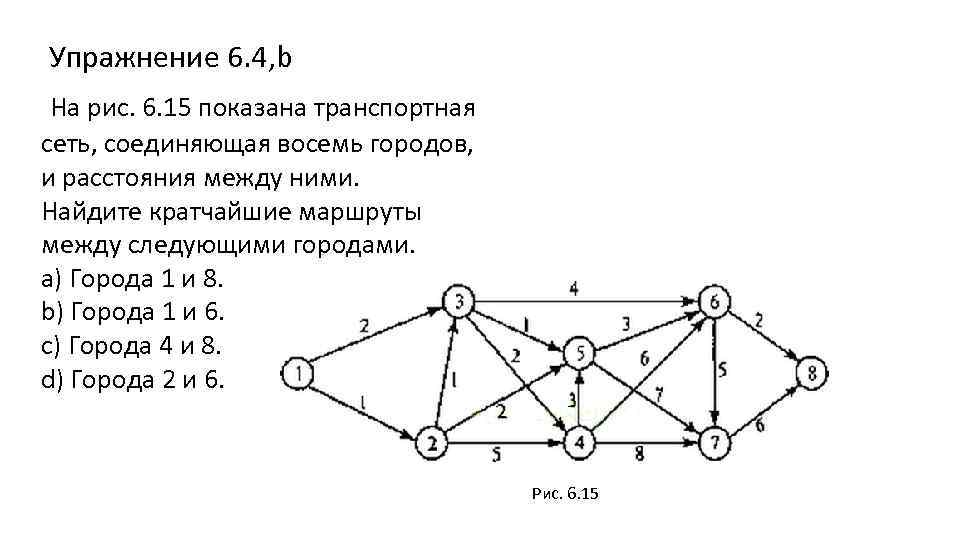Упражнение 6. 4, b На рис. 6. 15 показана транспортная сеть, соединяющая восемь городов, и расстояния между ними. Найдите кратчайшие маршруты между следующими городами. a) Города 1 и 8. b) Города 1 и 6. c) Города 4 и 8. d) Города 2 и 6. Рис. 6. 15

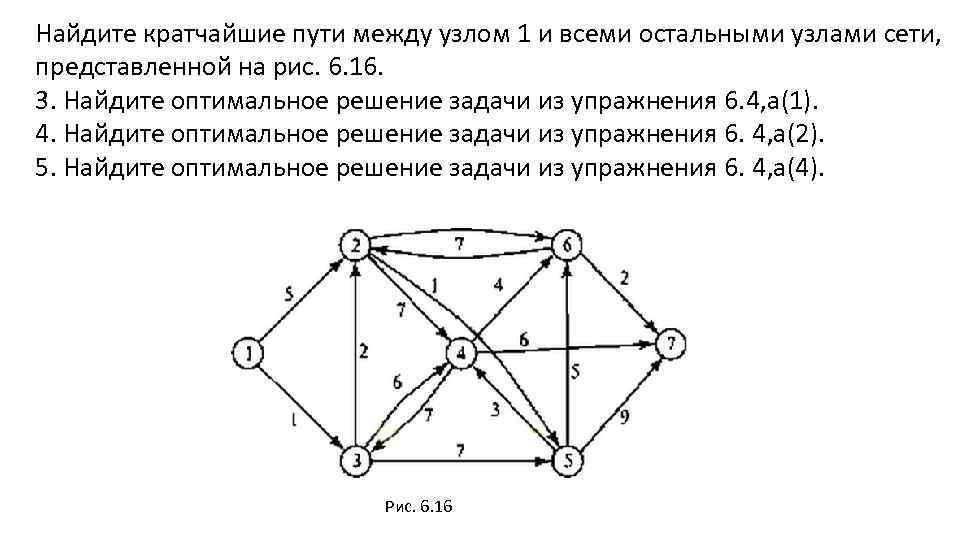Найдите кратчайшие пути между узлом 1 и всеми остальными узлами сети, представленной на рис. 6. 16. 3. Найдите оптимальное решение задачи из упражнения 6. 4, a(1). 4. Найдите оптимальное решение задачи из упражнения 6. 4, a(2). 5. Найдите оптимальное решение задачи из упражнения 6. 4, a(4). Рис. 6. 16

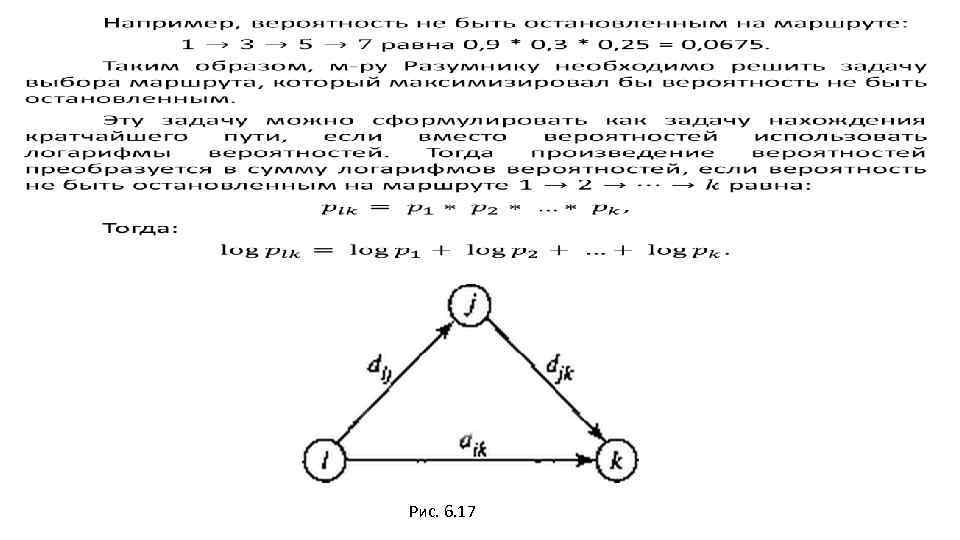Рис. 6. 17

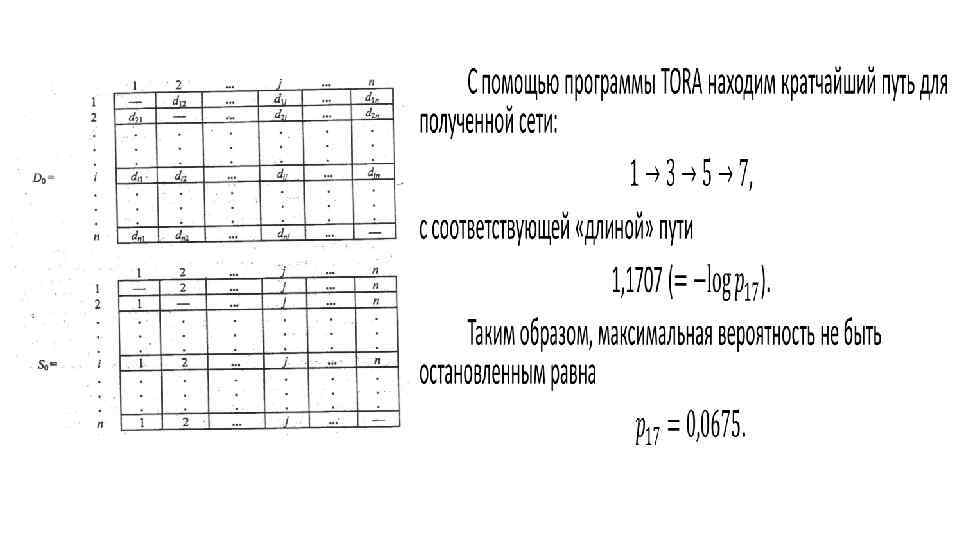
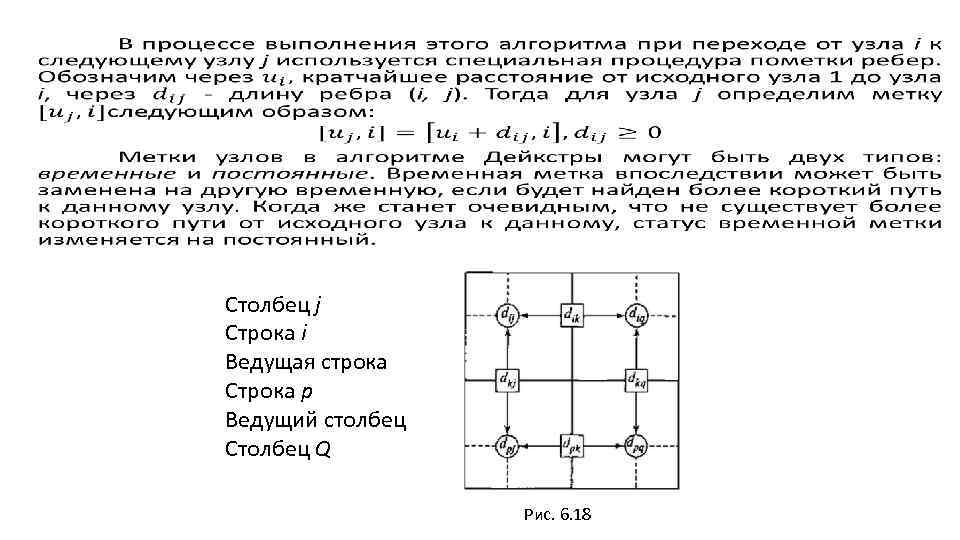Столбец j Строка i Ведущая строка Строка р Ведущий столбец Столбец Q Рис. 6. 18

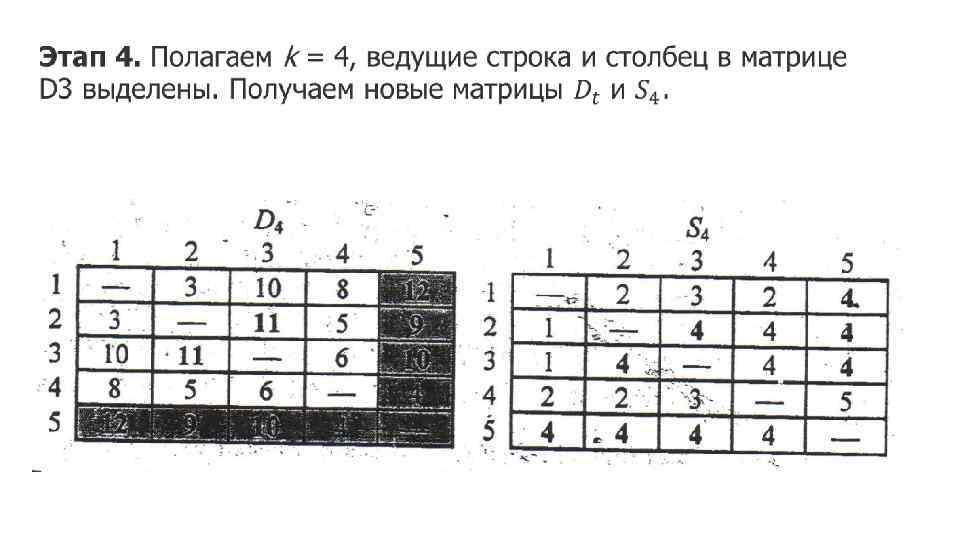
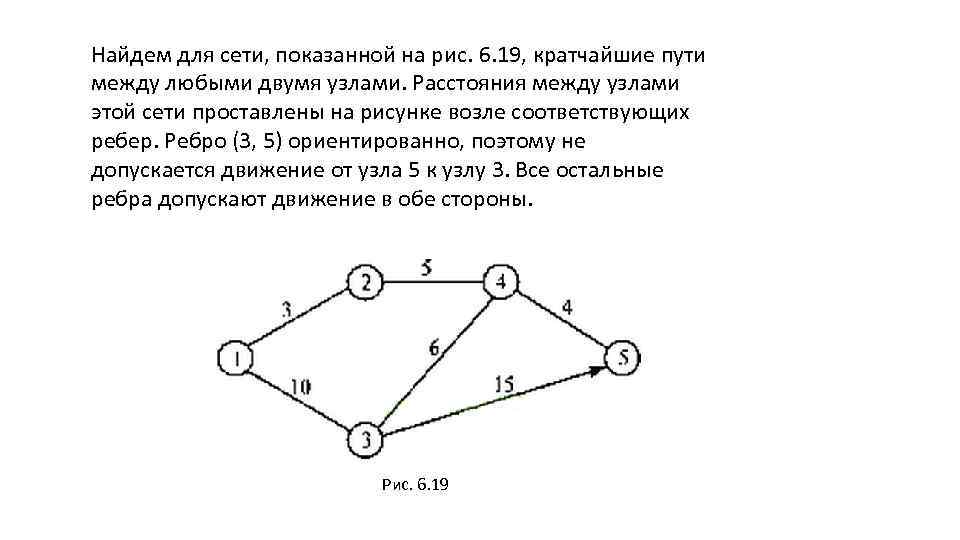Найдем для сети, показанной на рис. 6. 19, кратчайшие пути между любыми двумя узлами. Расстояния между узлами этой сети проставлены на рисунке возле соответствующих ребер. Ребро (3, 5) ориентированно, поэтому не допускается движение от узла 5 к узлу 3. Все остальные ребра допускают движение в обе стороны. Рис. 6. 19

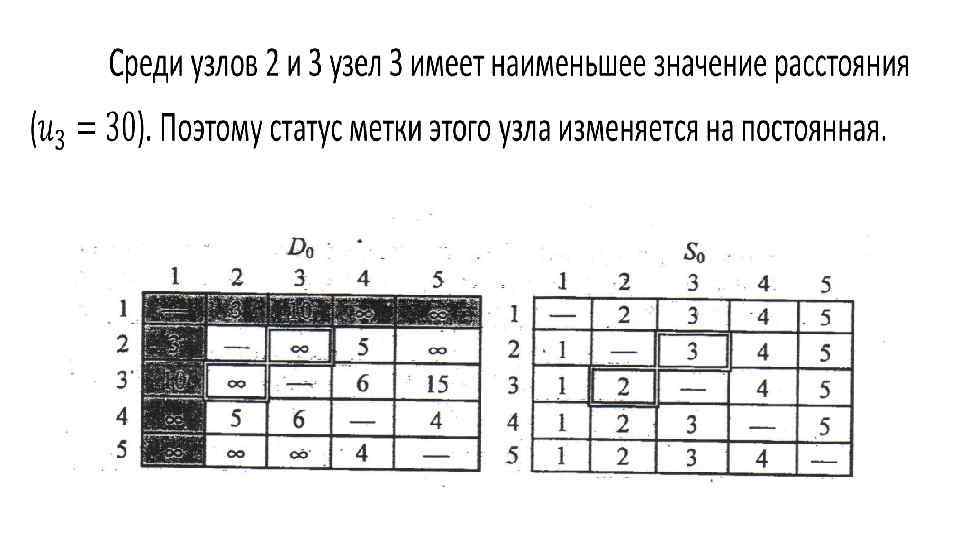
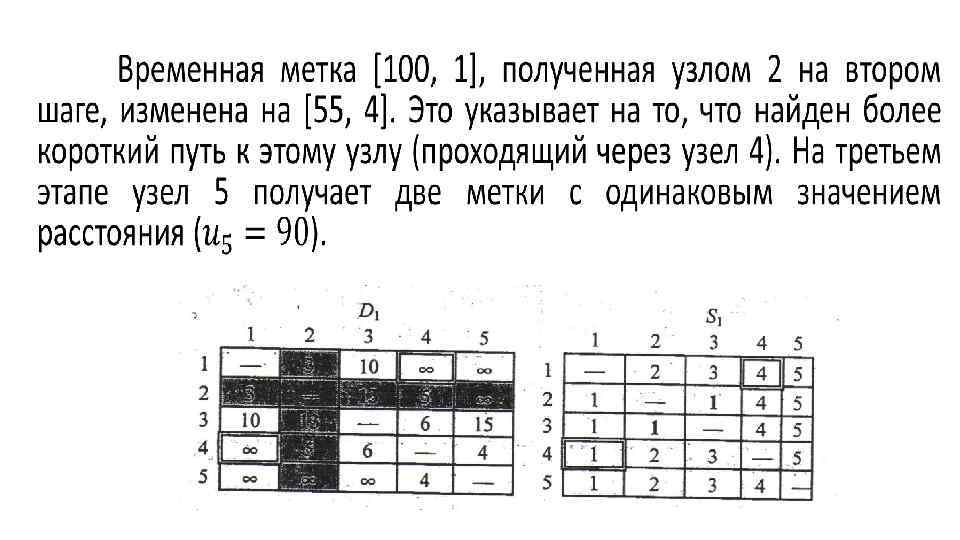
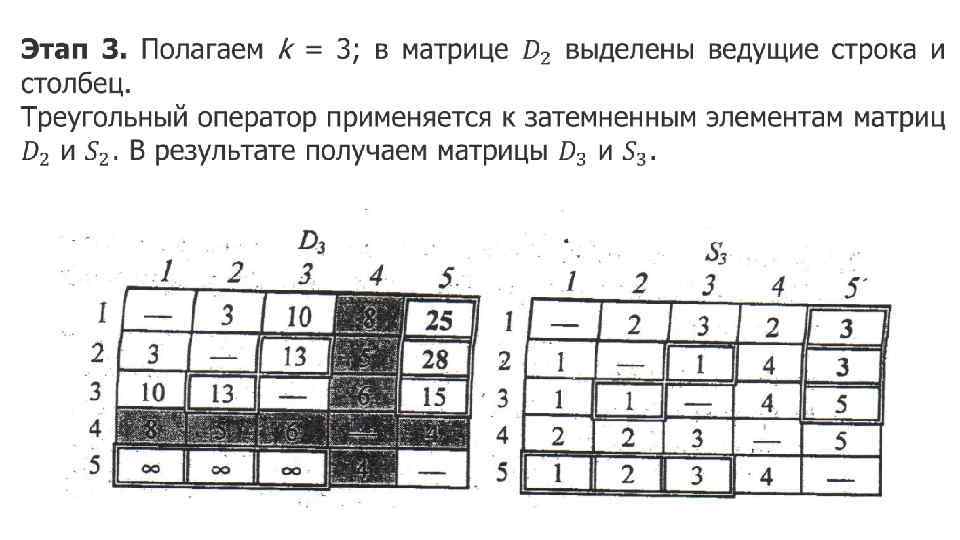
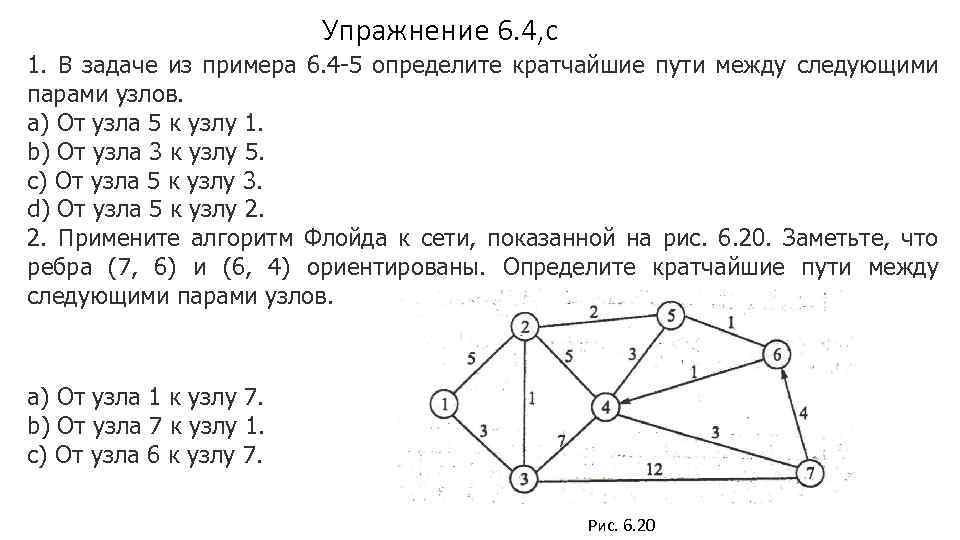Упражнение 6. 4, с 1. В задаче из примера 6. 4 -5 определите кратчайшие пути между следующими парами узлов. a) От узла 5 к узлу 1. b) От узла 3 к узлу 5. c) От узла 5 к узлу 3. d) От узла 5 к узлу 2. 2. Примените алгоритм Флойда к сети, показанной на рис. 6. 20. Заметьте, что ребра (7, 6) и (6, 4) ориентированы. Определите кратчайшие пути между следующими парами узлов. a) От узла 1 к узлу 7. b) От узла 7 к узлу 1. c) От узла 6 к узлу 7. Рис. 6. 20

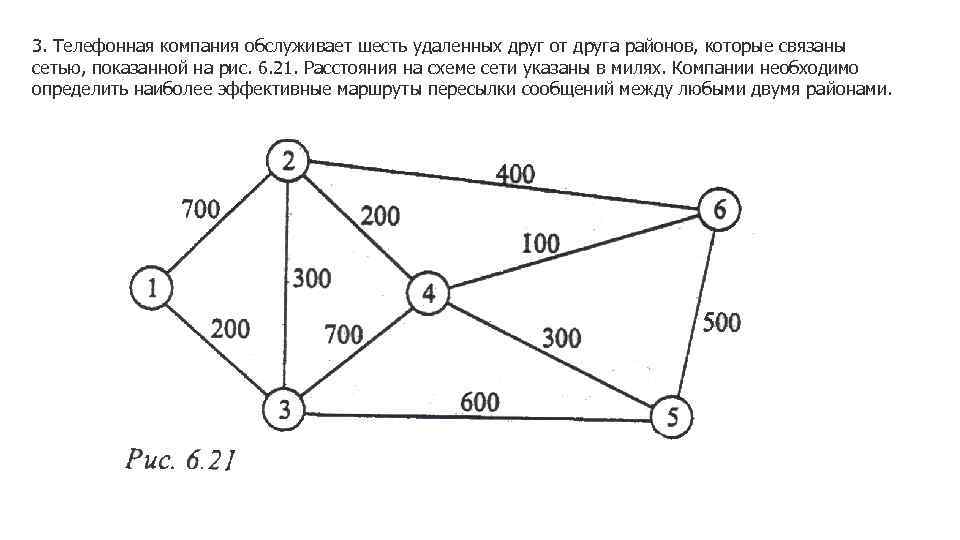3. Телефонная компания обслуживает шесть удаленных друг от друга районов, которые связаны сетью, показанной на рис. 6. 21. Расстояния на схеме сети указаны в милях. Компании необходимо определить наиболее эффективные маршруты пересылки сообщений между любыми двумя районами.