Задача на формулу комбинаторики Выполняли ученицы 9» Б» класса: Фонтенелева Анна; Соловьева Наталья; Молоштан Анна
Задача: Дана шахматная доска и 2 коня. Сколькими способами можно поставить на шахматную доску 2 коня, чтобы они не били друга? Для решения этой задачи существует 4 способа. По отдельности рассмотрим каждый из них. 2
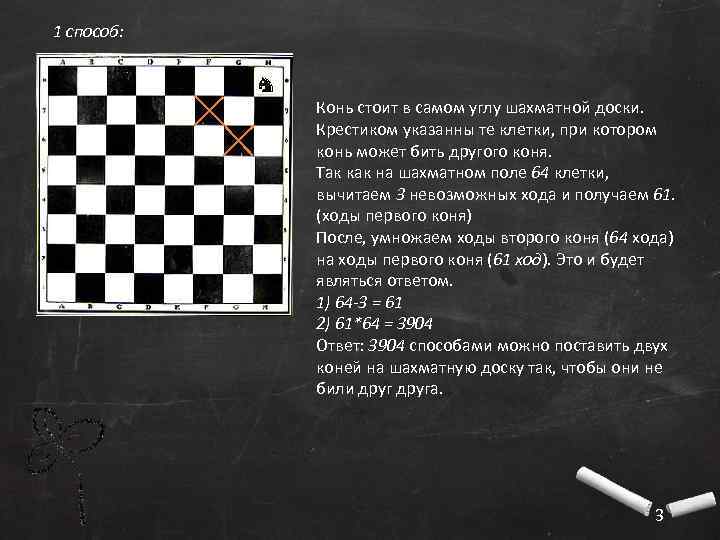
1 способ: Конь стоит в самом углу шахматной доски. Крестиком указанны те клетки, при котором конь может бить другого коня. Так как на шахматном поле 64 клетки, вычитаем 3 невозможных хода и получаем 61. (ходы первого коня) После, умножаем ходы второго коня (64 хода) на ходы первого коня (61 ход). Это и будет являться ответом. 1) 64 -3 = 61 2) 61*64 = 3904 Ответ: 3904 способами можно поставить двух коней на шахматную доску так, чтобы они не били друга. 3
2 способ: 64 хода первого коня умножаем на 55 ходов второго коня (так как на шахматном поле 64 клетки, вычитаем 9 невозможных ходов и получаем 55). 1) 64 -9 = 55 2) 64*55 = 3520 Ответ: 3520 способами можно поставить двух коней на шахматную доску так, чтобы они не били друга. 4
3 способ: 64 хода первого коня умножаем на 60 ходов второго коня (так как на шахматном поле 64 клетки, вычитаем 4 невозможных ходов и получаем 60). 1) 64 -4 = 60 2) 64*56 = 3840 Ответ: 3840 способами можно поставить двух коней на шахматную доску так, чтобы они не били друга. 5
4 способ: 64 хода первого коня умножаем на 59 ходов второго коня (так как на шахматном поле 64 клетки, вычитаем 5 невозможных ходов и получаем 60). 1) 64 -5 = 59 2) 64*59 = 3776 Ответ: 3776 способами можно поставить двух коней на шахматную доску так, чтобы они не били друга. 6
Спасибо за внимание! 7
Скачать презентацию Задача на формулу комбинаторики Выполняли ученицы 9 Б
задача.pptx