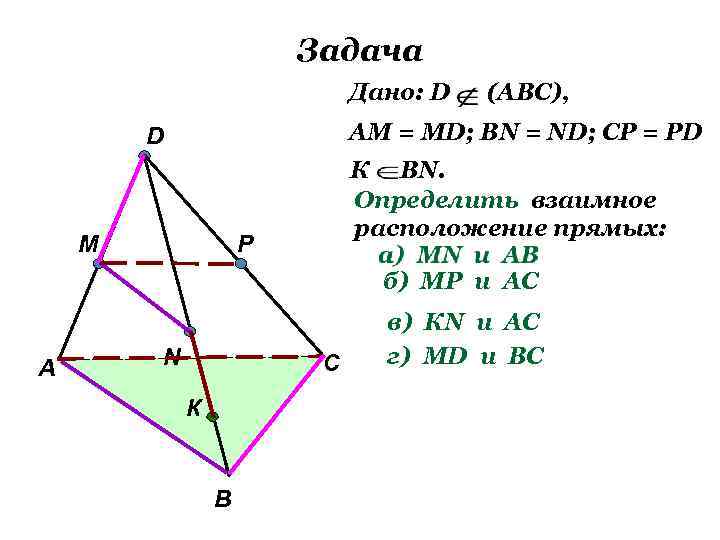
 Задача Дано: D (АВС), АМ = МD; ВN = ND; CP = PD D M К ВN. Определить взаимное расположение прямых: P б) МР и AС А N С К В в) КN и AС г) МD и BС
Задача Дано: D (АВС), АМ = МD; ВN = ND; CP = PD D M К ВN. Определить взаимное расположение прямых: P б) МР и AС А N С К В в) КN и AС г) МD и BС
 Верны ли утверждения: 1. Если две прямые не имеют общих точек, то они параллельны? нет 2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а)пересекаться? да б)быть скрещивающимися? да 3. Могут ли две скрещивающиеся прямые быть параллельными третьей прямой? нет 4. Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, нет что прямые а и с – скрещивающиеся? 5. Каково должно быть взаимное положение трех прямых, чтобы можно было провести плоскость, содержащую все прямые?
Верны ли утверждения: 1. Если две прямые не имеют общих точек, то они параллельны? нет 2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а)пересекаться? да б)быть скрещивающимися? да 3. Могут ли две скрещивающиеся прямые быть параллельными третьей прямой? нет 4. Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, нет что прямые а и с – скрещивающиеся? 5. Каково должно быть взаимное положение трех прямых, чтобы можно было провести плоскость, содержащую все прямые?
 Проверка ДЗ № 35 1. Предположит, что а и b не скрещивающиеся Через а и b проведем плоскость β. или 2. Предположим, что а не скрещивается с с Через а и с проведем плоскость γ. 3. 4. или а – линия пересечения плоскостей β и γ. что противоречит условию. 5. Следовательно, а и b скрещивающиеся или а и с скрещивающиеся. а b c М
Проверка ДЗ № 35 1. Предположит, что а и b не скрещивающиеся Через а и b проведем плоскость β. или 2. Предположим, что а не скрещивается с с Через а и с проведем плоскость γ. 3. 4. или а – линия пересечения плоскостей β и γ. что противоречит условию. 5. Следовательно, а и b скрещивающиеся или а и с скрещивающиеся. а b c М
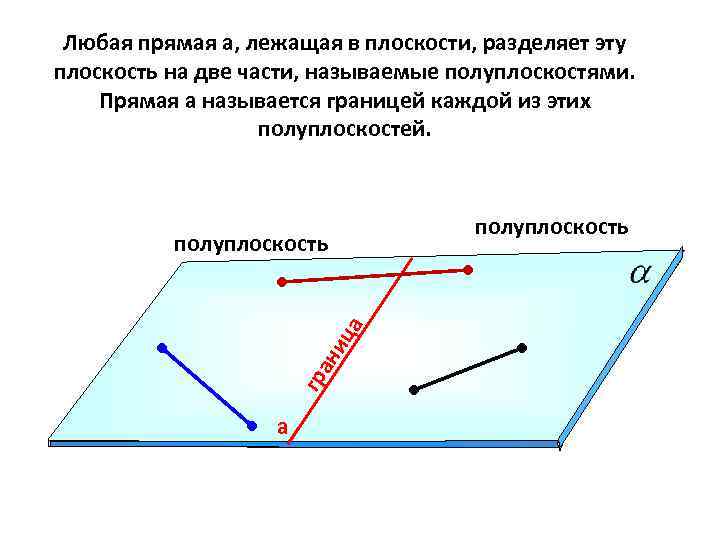 Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. полуплоскость гр ан иц а полуплоскость а
Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. полуплоскость гр ан иц а полуплоскость а
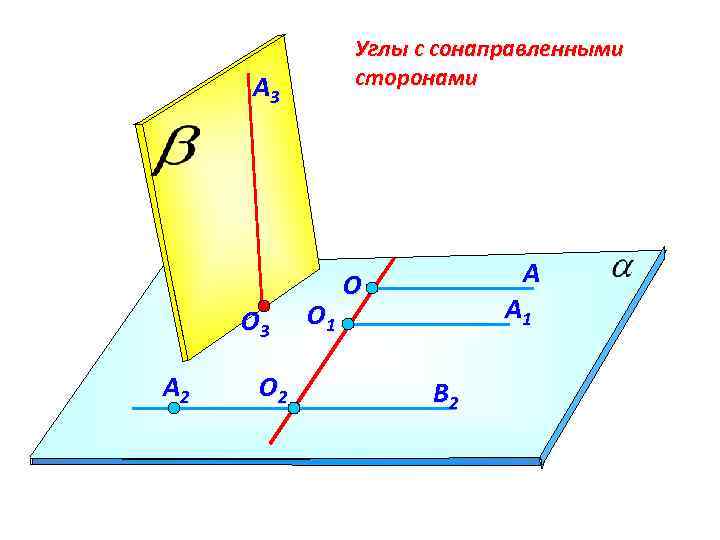 Углы с сонаправленными сторонами A 3 О 3 A 2 О 1 A A 1 О В 2
Углы с сонаправленными сторонами A 3 О 3 A 2 О 1 A A 1 О В 2
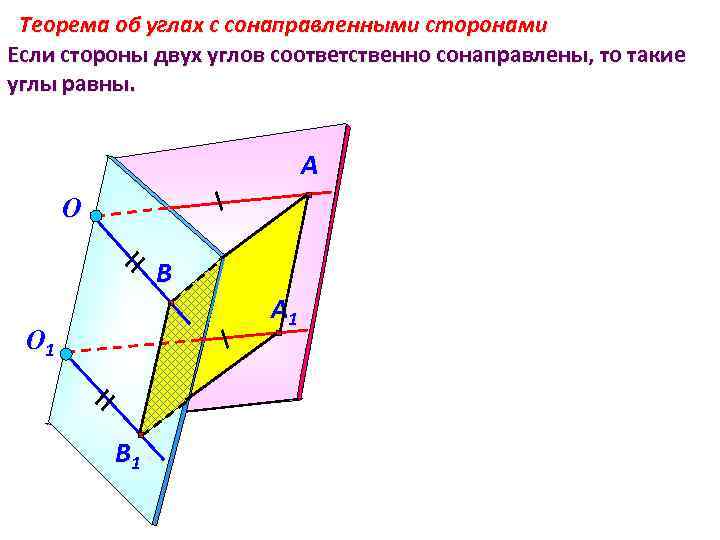 Теорема об углах с сонаправленными сторонами Если стороны двух углов соответственно сонаправлены, то такие углы равны. A О B A 1 О 1 B 1
Теорема об углах с сонаправленными сторонами Если стороны двух углов соответственно сонаправлены, то такие углы равны. A О B A 1 О 1 B 1
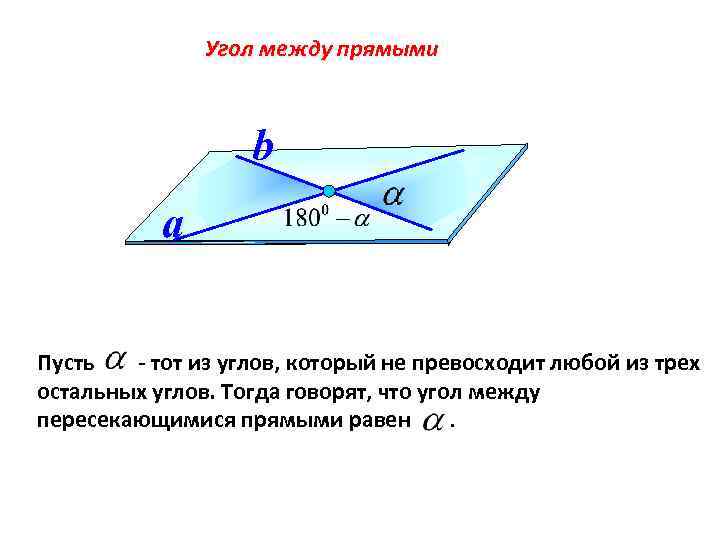 Угол между прямыми b a Пусть - тот из углов, который не превосходит любой из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен.
Угол между прямыми b a Пусть - тот из углов, который не превосходит любой из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен.
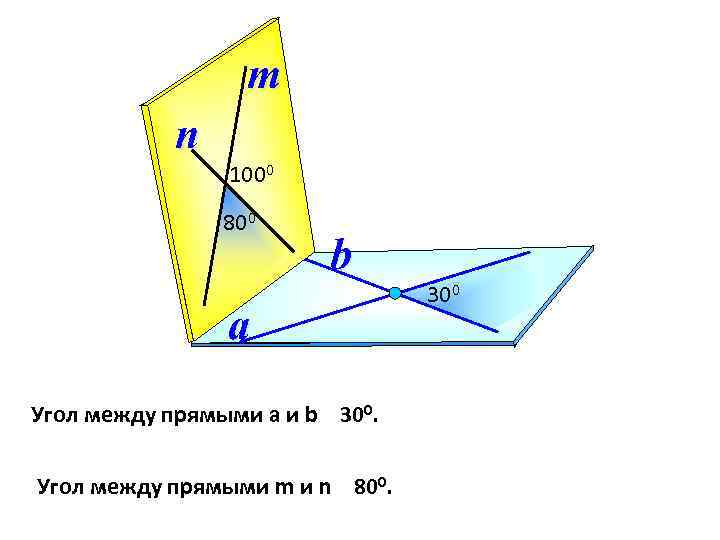 m n 1000 800 b a Угол между прямыми а и b 300. Угол между прямыми m и n 800. 300
m n 1000 800 b a Угол между прямыми а и b 300. Угол между прямыми m и n 800. 300
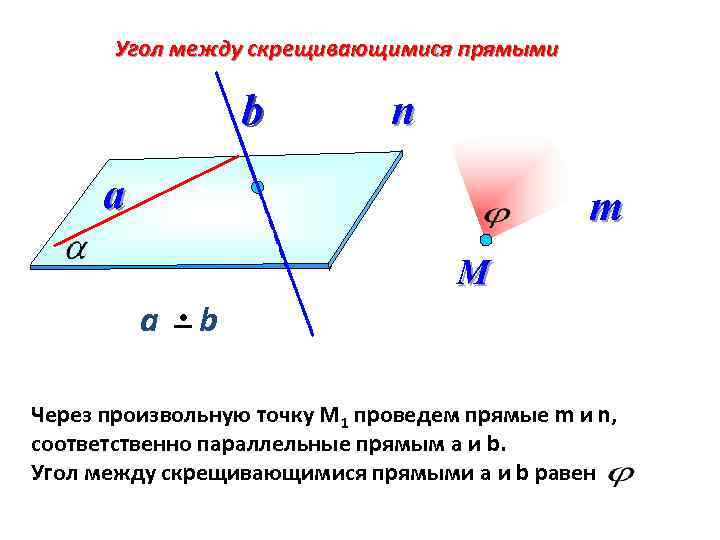 Угол между скрещивающимися прямыми b n a m М а b Через произвольную точку М 1 проведем прямые m и n, соответственно параллельные прямым a и b. Угол между скрещивающимися прямыми a и b равен
Угол между скрещивающимися прямыми b n a m М а b Через произвольную точку М 1 проведем прямые m и n, соответственно параллельные прямым a и b. Угол между скрещивающимися прямыми a и b равен
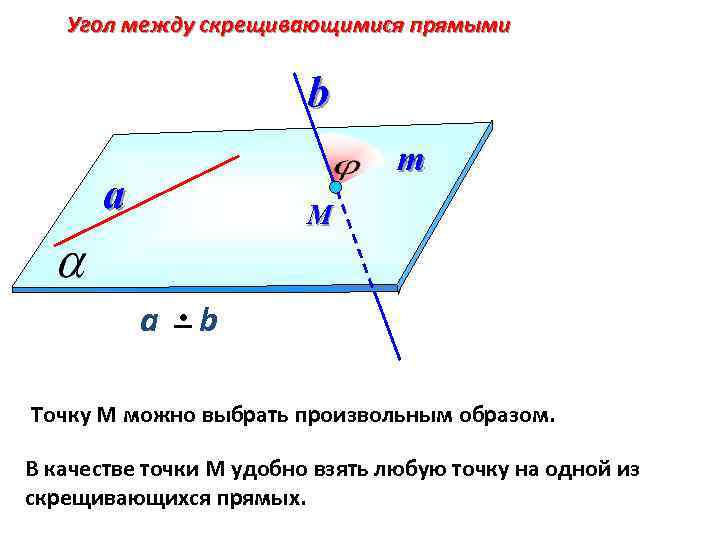 Угол между скрещивающимися прямыми b m a М а b Точку М можно выбрать произвольным образом. В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.
Угол между скрещивающимися прямыми b m a М а b Точку М можно выбрать произвольным образом. В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.
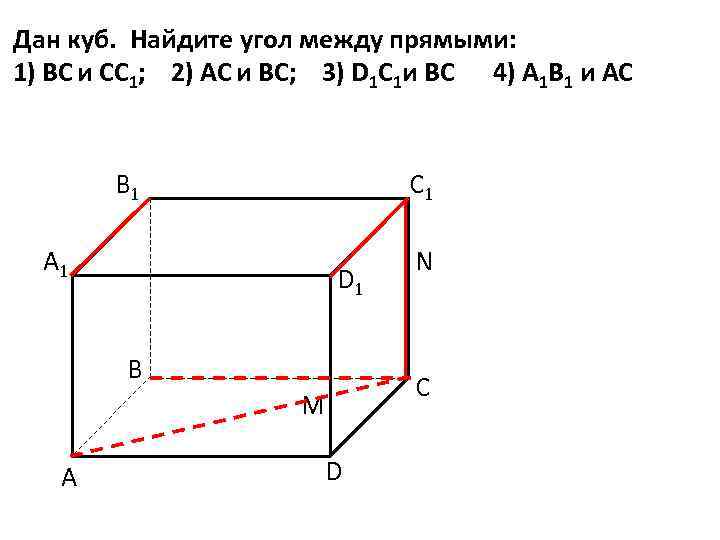 Дан куб. Найдите угол между прямыми: 1) ВС и СC 1; 2) AС и ВC; 3) D 1 C 1 и BC 4) A 1 B 1 и AC B 1 С 1 А 1 D 1 В С M А N D
Дан куб. Найдите угол между прямыми: 1) ВС и СC 1; 2) AС и ВC; 3) D 1 C 1 и BC 4) A 1 B 1 и AC B 1 С 1 А 1 D 1 В С M А N D
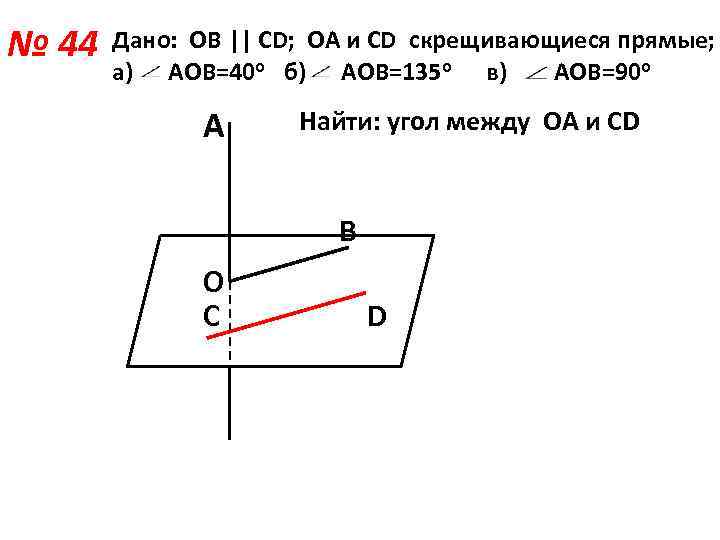 № 44 Дано: ОВ || CD; ОА и CD скрещивающиеся прямые; а) АОВ=40 о б) АОВ=135 о в) АОВ=90 о А Найти: угол между ОА и СD В О С D
№ 44 Дано: ОВ || CD; ОА и CD скрещивающиеся прямые; а) АОВ=40 о б) АОВ=135 о в) АОВ=90 о А Найти: угол между ОА и СD В О С D
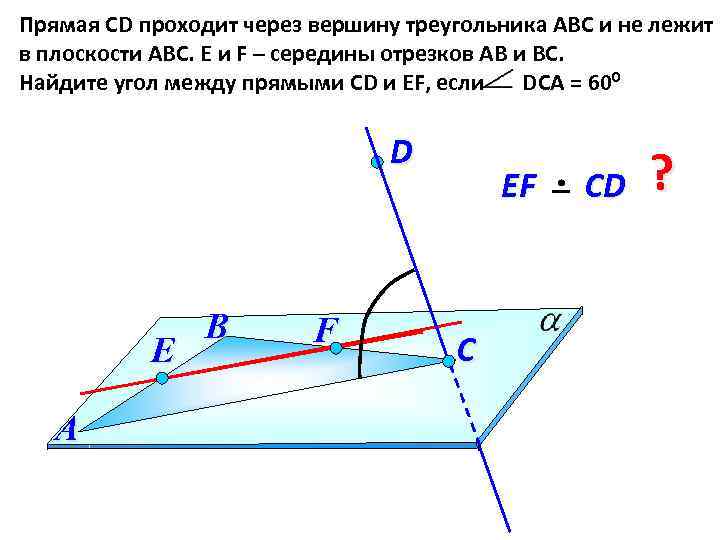 Прямая СD проходит через вершину треугольника АВС и не лежит в плоскости АВС. E и F – середины отрезков АВ и ВС. Найдите угол между прямыми СD и EF, если DCA = 600 D E А В F EF C СD ?
Прямая СD проходит через вершину треугольника АВС и не лежит в плоскости АВС. E и F – середины отрезков АВ и ВС. Найдите угол между прямыми СD и EF, если DCA = 600 D E А В F EF C СD ?
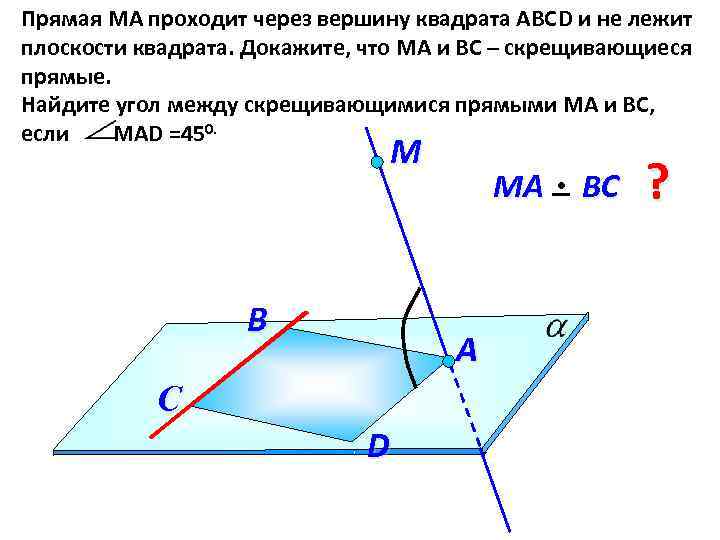 Прямая МА проходит через вершину квадрата АВСD и не лежит плоскости квадрата. Докажите, что МА и ВС – скрещивающиеся прямые. Найдите угол между скрещивающимися прямыми МА и ВС, если МАD =450. М B МА А С D ВС ?
Прямая МА проходит через вершину квадрата АВСD и не лежит плоскости квадрата. Докажите, что МА и ВС – скрещивающиеся прямые. Найдите угол между скрещивающимися прямыми МА и ВС, если МАD =450. М B МА А С D ВС ?
 Домашнее задание 1. п. 8, 9 опр. и док-во 2. № 40; 42
Домашнее задание 1. п. 8, 9 опр. и док-во 2. № 40; 42