Задача № 1 Выполнил студент группы ЭГП-1 -12 Сафаров Зафар Вариант 12
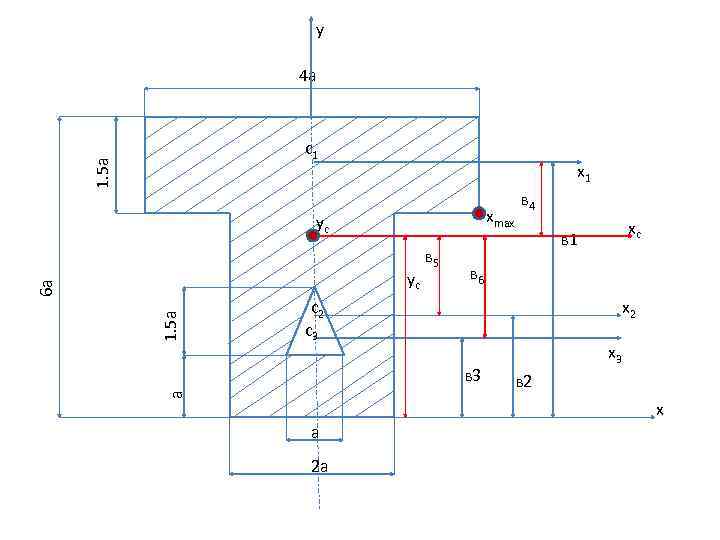у 4 а 1. 5 а с1 x 1 хmax ус 1. 5 а 6 а yc в 5 в 4 в 6 с2 с3 x 2 в 3 а xc в 1 x 3 в 2 x а 2 а
РЕШЕНИЕ 1) Разбиваем сечение на простые фигуры. x 1 x 2 2)Проводим центральные оси каждой фигуры через их центры тяжести. 3)Выбираем систему координат 4)Определяем расстояние между осями х и х1, х2, х3: в 1= 5, 25 а в 2 = 2, 25 а в 3=2 а 5) Определяем общую площадь сечения: А= А 1+А 2 -А 3 А 1=6 а 2 А 2=9 а 2 А 3=0, 75 а 2 А=14, 75 а 2 x 3
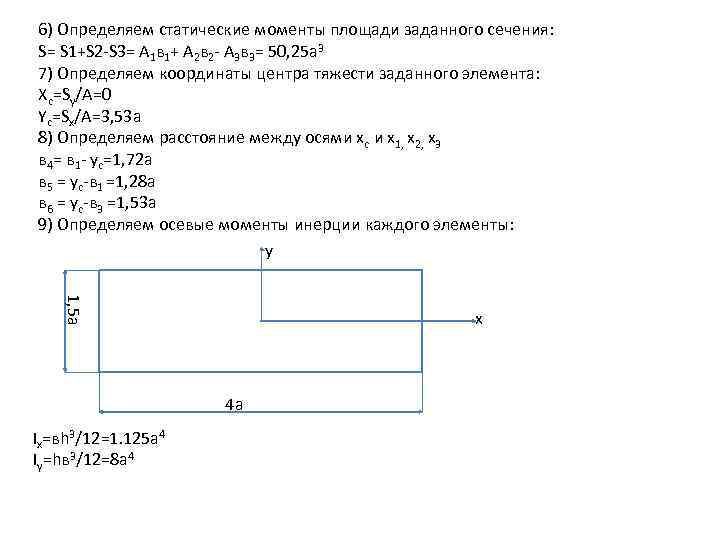6) Определяем статические моменты площади заданного сечения: S= S 1+S 2 -S 3= A 1 в 1+ A 2 в 2 - A 3 в 3= 50, 25 а 3 7) Определяем координаты центра тяжести заданного элемента: Хс=Sy/A=0 Yс=Sx/A=3, 53 a 8) Определяем расстояние между осями хс и х1, х2, х3 в 4= в 1 - yc=1, 72 а в 5 = yc-в 1 =1, 28 а в 6 = yc-в 3 =1, 53 а 9) Определяем осевые моменты инерции каждого элементы: у 1, 5 а х 4 а Ix=вh 3/12=1. 125 a 4 Iy=hв 3/12=8 a 4
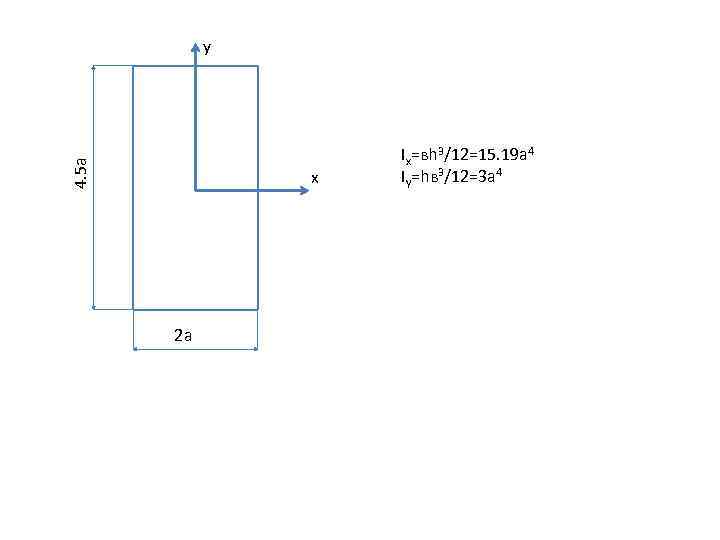4. 5 a y x 2 a Ix=вh 3/12=15. 19 a 4 Iy=hв 3/12=3 a 4
y 1. 5 a Ix=вh 3/36=0. 094 a 4 Iy=hв 3/48=0. 031 a 4 x a 10) Определяем осевые моменты инерции заданного сечения относительно хс: Ixc= Ixc 1+ Ixc 2 - Ixc 3= 46. 97 a 4 Ixc 1=Ix 1+A 1 в 24 =18, 88 а 4 Ixc 2=Ix 2+A 2 в 25 =29, 94 а 4 Ixc 3=Ix 3+A 3 в 26 =1, 85 а 4 11) Определяем осевые моменты относительно ус : Iуc= Iуc 1+ Iуc 2 - Iуc 3= 23, 159 a 4 12) Определяем моменты сопротивления: Wxc = Ixc/ymax= Ixc/yc =13. 31 a 3 Wyc = Iyc/ymax=11. 58 a 3
13) Определяем радиус инерции сечения: ixc=(Ixc/A)1/2=1. 81 a iyc=(Iyc/A)1/2=1. 28 a Подставим исходное значение «а» в полученные результаты: Wxc = Ixc/ymax= Ixc/yc =13. 31 a 3=207, 97 см Wyc = Iyc/ymax=11. 58 a 3 =180, 94 см ixc=(Ixc/A)1/2=1. 81 a=4. 53 см iyc=(Iyc/A)1/2=1. 28 a=3, 2 см Ixc= Ixc 1+ Ixc 2 - Ixc 3= 46. 97 a 4=1834, 77 кг*см 2 Ixc 1=Ix 1+A 1 в 24 =18, 88 а 4=737, 5 кг*см 2 Ixc 2=Ix 2+A 2 в 25 =29, 94 а 4=1169, 53 кг*см 2 Ixc 3=Ix 3+A 3 в 26 =1, 85 а 4=72, 27 кг*см 2 Iуc= Iуc 1+ Iуc 2 - Iуc 3= 23, 159 a 4=904, 65 кг*см 2 Yс=Sx/A=3, 53 a=8, 825 см