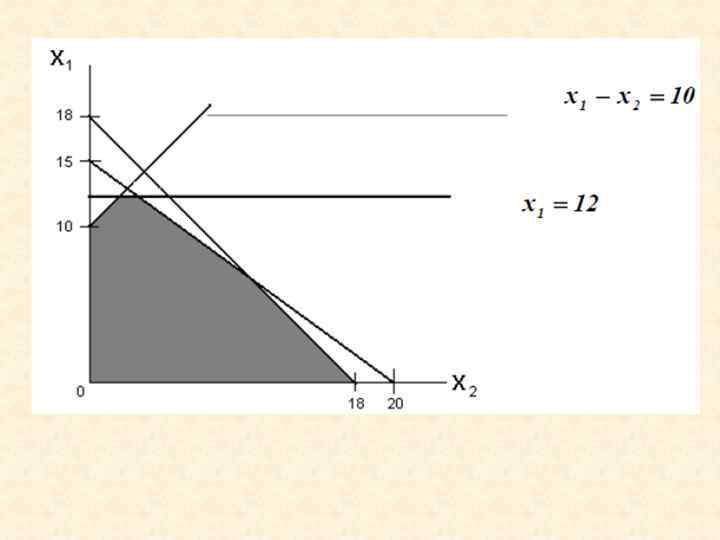
Задача 1 Найти максимальное значение целевой функции F

Задача 1 Найти максимальное значение целевой функции F = 4 x 1+3 x 2 → max, при системе ограничений: 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 1≥ 0 (3) x 2≥ 0 (4) где x 1, x 1 - целые числа. Построим область допустимых решений, т. е. решим графически систему неравенств (для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

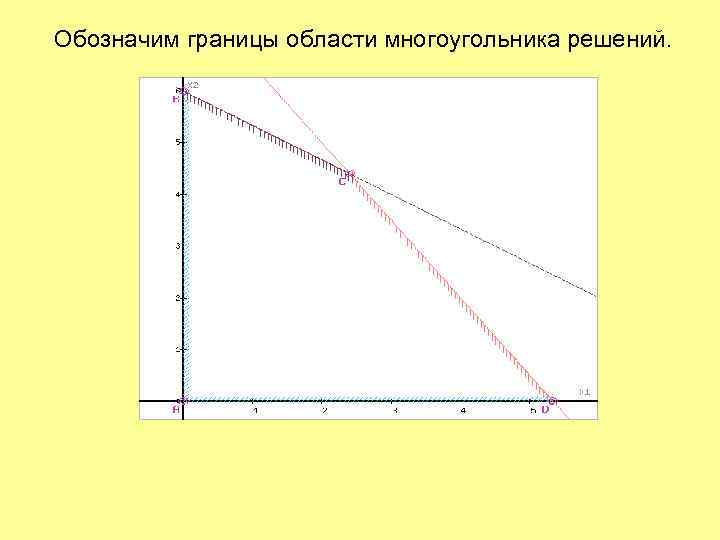Обозначим границы области многоугольника решений.

Рассмотрим целевую функцию задачи F = 4 x 1+3 x 2 → max. Построим прямую, отвечающую значению функции F = 0: F = 4 x 1+3 x 2 = 0. Поскольку нас интересует максимальное решение, поэтому будем двигать прямую параллельным образом до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

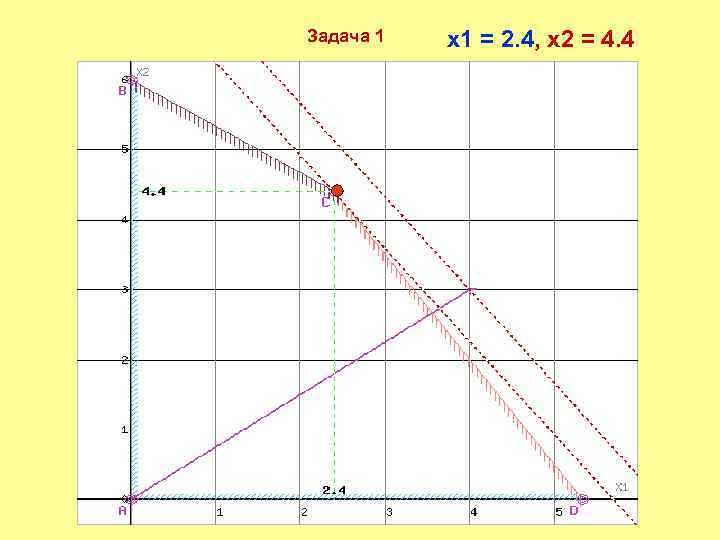Задача 1 x 1 = 2. 4, x 2 = 4. 4

Область допустимых решений представляет собой многоугольник. Прямая F(x) = const пересекает область в точке C, которая получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 Решив систему уравнений, получим: x 1 = 2. 4, x 2 = 4. 4 Откуда найдем максимальное значение целевой функции: F(X) = 4*2. 4 + 3*4. 4 = 22. 8 Оптимальное значение переменной x 1=2. 4 оказалось нецелочисленным.

Разбиваем задачу 1 на две подзадачи 11 и 12. В первой из них к условиям задачи 11 добавляется условие х1 ≥ 3, а к задаче 12 — условие х1 ≤ 2. Эта процедура называется ветвлением по переменной х1. Решим графически задачу 11 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 1≥ 3 (3) x 1≥ 0 (4) x 2≥ 0 (5) Область допустимых решений представляет собой треугольник.

Прямая F(x) = const пересекает область в точке B. (получена в результате пересечения прямых (1) и (3)), ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 x 1≥ 3 Решив систему уравнений, получим: x 1 = 3, x 2 = 3. 5 Откуда найдем максимальное значение целевой функции: F(X) = 4*3 + 3*3. 5 = 22. 5

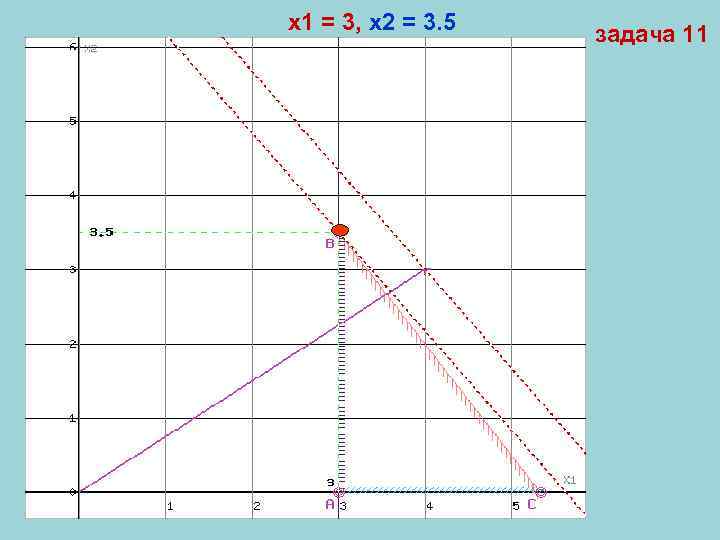x 1 = 3, x 2 = 3. 5 задача 11

Решим графически задачу 12 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 1≤ 2 (3) x 1≥ 0 (4) x 2≥ 0 (5) Область допустимых решений представляет собой многоугольник. Прямая F(x) = const пересекает область в точке D, которая получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых: 2 x 1+3 x 2≤ 18 x 1≤ 2 Решив систему уравнений, получим: x 1 = 2, x 2 = 4. 6667 Откуда найдем максимальное значение целевой функции: F(X) = 4*2 + 3*4. 6667 = 22

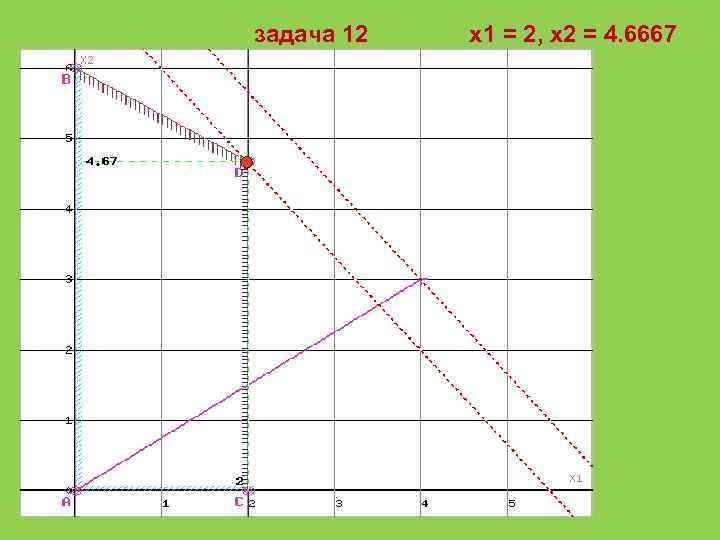задача 12 x 1 = 2, x 2 = 4. 6667

Оптимальное значение переменной x 2=3. 5 оказалось нецелочисленным. Разбиваем задачу 11 на две подзадачи 111 и 112. В первой из них к условиям задачи 111 добавляется условие х2 ≥ 4, а к задаче 112 — условие х2 ≤ 3. Решим графически задачу 111 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 1≥ 3 (3) x 2≥ 4 (4) x 1≥ 0 (5) x 2≥ 0 (6) Задача не имеет допустимых решений. ОДР представляет собой пустое множество (рис. б).

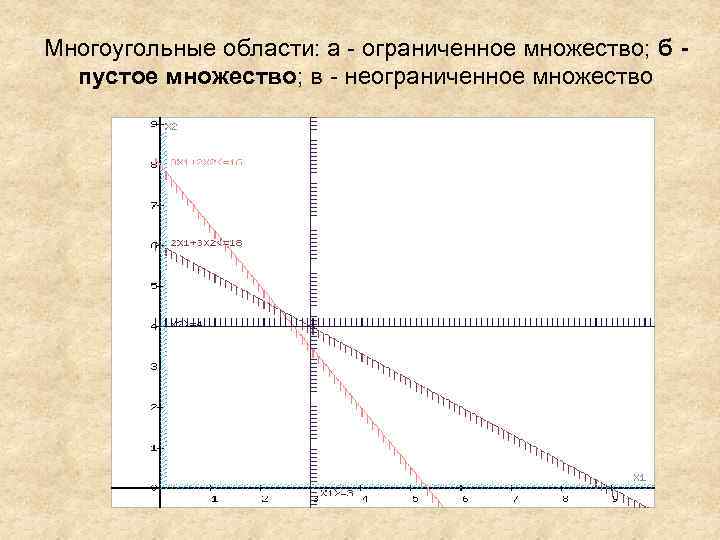Многоугольные области: а - ограниченное множество; б - пустое множество; в - неограниченное множество

Задача 111 не имеет решения, поэтому для нее процесс ветвления прерываем. Решим графически задачу 112 как задачу ЛП 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 1≥ 3 x 2≤ 3 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6)

Область допустимых решений представляет собой многоугольник Прямая F(x) = const пересекает область в точке C, которая получена в результате пересечения прямых (1) и (4), ее координаты удовлетворяют уравнениям этих прямых 3 x 1+2 x 2≤ 16 x 2≤ 3 Решив систему уравнений, получим: x 1 = 3. 3333, x 2 = 3 Откуда найдем максимальное значение целевой функции: F(X) = 4*3. 3333 + 3*3 = 22. 3333

Оптимальное значение переменной x 1=3. 33 оказалось нецелочисленным. Разбиваем задачу 112 на две подзадачи 1121 и 1122. В первой из них к условиям задачи 1121 добавляется условие х1 ≥ 4, а к задаче 1122 — условие х1 ≤ 3. Решим графически задачу 1121 как задачу ЛП. 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 1≥ 3 x 2≤ 3 x 1≥ 4 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7)

Область допустимых решений представляет собой треугольник. Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (5), то ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 x 1≥ 4 Решив систему уравнений, получим: x 1 = 4, x 2 = 2 Откуда найдем максимальное значение целевой функции: F(X) = 4*4 + 3*2 = 22

Решение задачи получилось целочисленным. Новое значение текущего рекорда будет равно F(X) = 22. Так как найденная точка является первым целочисленным решением, то ее и соответствующее ей значение ЦФ следует запомнить. Сама точка называется текущим целочисленным рекордом или просто рекордом, а оптимальное значение целочисленной задачи — текущим значением рекорда. Это значение является нижней границей оптимального значения исходной задачи Z*. Решим графически задачу 1122 как задачу ЛП.

Сведем систему ограничений к следующему виду: 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 1≥ 3 x 2≤ 3 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7) 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 1=3 (3) x 2≤ 3 (4) x 1≥ 0 (5) x 2≥ 0 (6)

Область допустимых решений представляет собой одну точку. Прямая F(x) = const пересекает область в точке B, которая получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых: x 1=3 x 2≤ 3 Решив систему уравнений, получим: x 1 = 3, x 2 = 3 Откуда найдем максимальное значение целевой функции: F(X) = 4*3 + 3*3 = 21 Текущий рекорд Z = 22 ≥ 21, поэтому прекращаем ветвление из этой вершины

22, 8 [2, 4; 4, 4] 22, 5 [3; 3, 5] пусто 12 11 111 22, 0 [4; 2] 1 1121 22, 3 [3, 3; 3] 1122 21, 0 [3; 3]

Для первой вершины оптимальное значение переменной x 2=4. 4 оказалось нецелочисленным. Разбиваем задачу 1 на две подзадачи 11 и 12. В первой из них к условиям задачи 11 добавляется условие х2 ≥ 5, а к задаче 12 — условие х2 ≤ 4. Эта процедура называется ветвлением по переменной х2.

Решим графически задачу 11 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 2≥ 5 (3) x 1≥ 0 (4) x 2≥ 0 (5)

Область допустимых решений представляет собой треугольник. Прямая F(x) = const пересекает область в точке C, еоторая получена в результате пересечения прямых (2) и (3), ее координаты удовлетворяют уравнениям этих прямых: 2 x 1+3 x 2≤ 18 x 2≥ 5 Решив систему уравнений, получим: x 1 = 1. 5, x 2 = 5 Откуда найдем максимальное значение целевой функции: F(X) = 4*1. 5 + 3*5 = 21

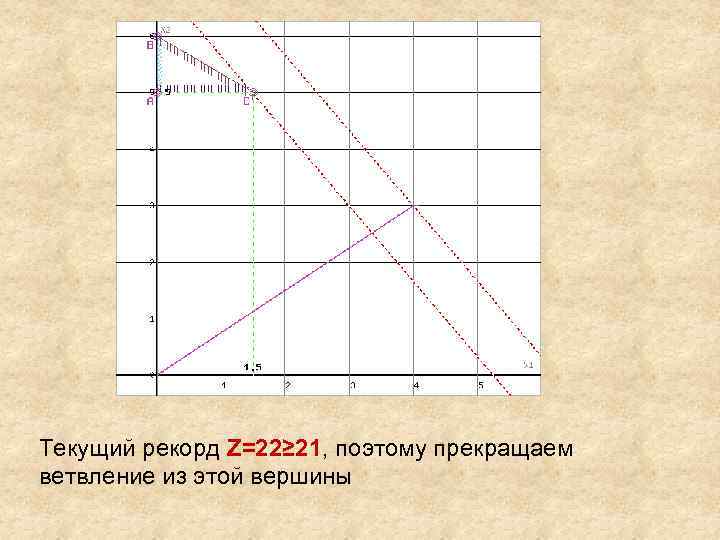Текущий рекорд Z=22≥ 21, поэтому прекращаем ветвление из этой вершины

Решим графически задачу 12 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 2≤ 4 (3) x 1≥ 0 (4) x 2≥ 0 (5)

Область допустимых решений представляет собой многоугольник Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 x 2≤ 4 Решив систему уравнений, получим: x 1 = 2. 6667, x 2 = 4 Откуда найдем максимальное значение целевой функции: F(X) = 4*2. 6667 + 3*4 = 22. 6667

Оптимальное значение переменной x 1=2. 67 оказалось нецелочисленным. Разбиваем задачу 12 на две подзадачи 121 и 122. В первой из них к условиям задачи 121 добавляется условие х1 ≥ 3, а к задаче 122 — условие х1 ≤ 2. Решим графически задачу 121 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 2≤ 4 (3) x 1≥ 3 (4) x 1≥ 0 (5) x 2≥ 0 (6)

Область допустимых решений представляет собой треугольник. Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (4), то ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 x 1≥ 3 Решив систему уравнений, получим: x 1 = 3, x 2 = 3. 5 Откуда найдем максимальное значение целевой функции: F(X) = 4*3 + 3*3. 5 = 22. 5

Решим графически задачу 122 как задачу ЛП. 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 2≤ 4 (3) x 1≤ 2 (4) x 1≥ 0 (5) x 2≥ 0 (6)

Область допустимых решений представляет собой многоугольник Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых: x 2≤ 4 x 1≤ 2 Решив систему уравнений, получим: x 1 = 2, x 2 = 4 Откуда найдем максимальное значение целевой функции: F(X) = 4*2 + 3*4 = 20

Текущий рекорд Z=22≥ 20, поэтому прекращаем ветвление из этой вершины Оптимальное значение переменной x 2=3. 5 оказалось нецелочисленным. Разбиваем задачу 121 на две подзадачи 1211 и 1212. В первой из них к условиям задачи 1211 добавляется условие х2 ≥ 4, а к задаче 1212 — условие х2 ≤ 3.

Решим графически задачу 1211 как задачу ЛП 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 2≤ 4 x 1≥ 3 x 2≥ 4 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7) Сведем систему ограничений к следующему виду: 3 x 1+2 x 2≤ 16 (1) 2 x 1+3 x 2≤ 18 (2) x 2=4 (3) x 1≥ 3 (4) x 1≥ 0 (5) x 2≥ 0 (6)

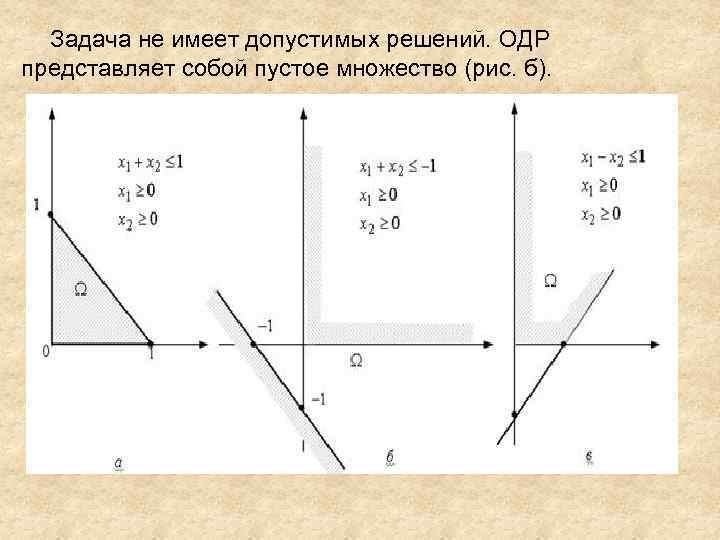Задача не имеет допустимых решений. ОДР представляет собой пустое множество (рис. б).

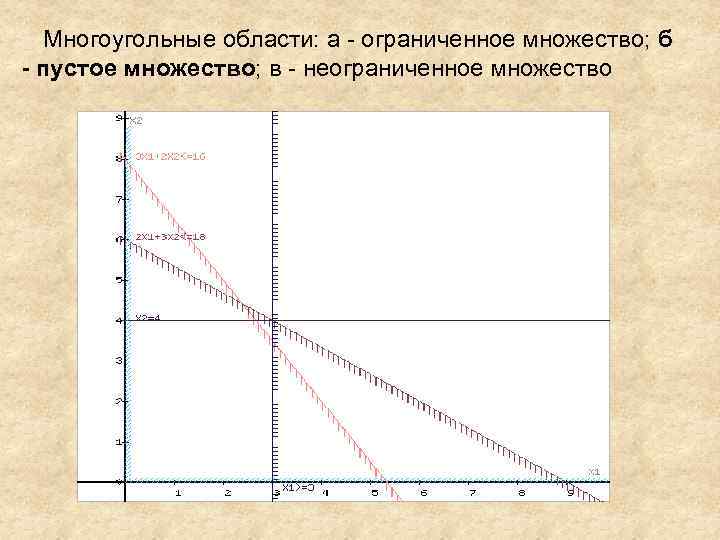Многоугольные области: а - ограниченное множество; б - пустое множество; в - неограниченное множество

Задача 1211 не имеет решения, поэтому для нее процесс ветвления прерываем. Решим графически задачу 1212 как задачу ЛП. 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 2≤ 4 x 1≥ 3 x 2≤ 3 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7)

Область допустимых решений представляет собой многоугольник Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (5), то ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 x 2≤ 3 Решив систему уравнений, получим: x 1 = 3. 3333, x 2 = 3 Откуда найдем максимальное значение целевой функции: F(X) = 4*3. 3333 + 3*3 = 22. 3333

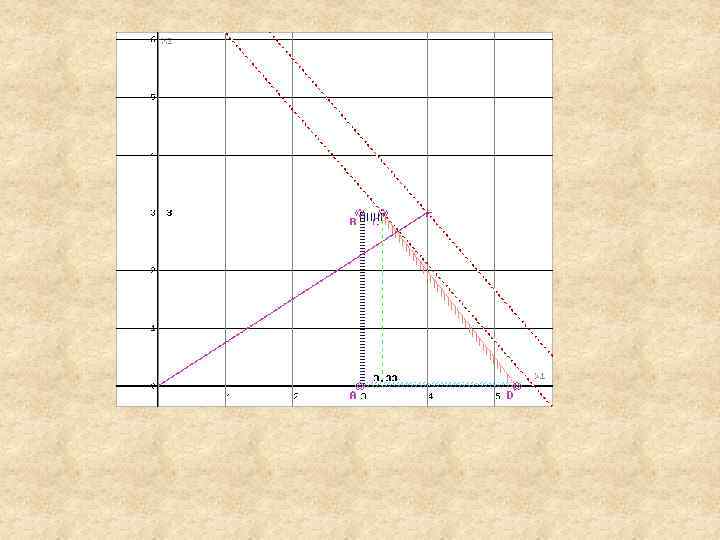
Оптимальное значение переменной x 1=3. 33 оказалось нецелочисленным. Разбиваем задачу 1212 на две подзадачи 12121 и 12122. В первой из них к условиям задачи 12121 добавляется условие х1 ≥ 4, а к задаче 12122 — условие х1 ≤ 3. Решим графически задачу 12121 как задачу ЛП. 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 2≤ 4 x 1≥ 3 x 2≤ 3 x 1≥ 4 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7) (8)

Область допустимых решений представляет собой треугольник. Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (6), то ее координаты удовлетворяют уравнениям этих прямых: 3 x 1+2 x 2≤ 16 x 1≥ 4 Решив систему уравнений, получим: x 1 = 4, x 2 = 2 Откуда найдем максимальное значение целевой функции: F(X) = 4*4 + 3*2 = 22

Текущий рекорд Z=22≥ 22, поэтому прекращаем ветвление из этой вершины Решим графически задачу 12122 как задачу ЛП. 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 2≤ 4 x 1≥ 3 x 2≤ 3 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7) (8) Сведем систему ограничений к следующему виду: 3 x 1+2 x 2≤ 16 2 x 1+3 x 2≤ 18 x 2≤ 4 x 1=3 x 2≤ 3 x 1≥ 0 x 2≥ 0 (1) (2) (3) (4) (5) (6) (7)

Область допустимых решений представляет собой одну точку. Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (4) и (5), то ее координаты удовлетворяют уравнениям этих прямых: x 1=3 x 2≤ 3 Решив систему уравнений, получим: x 1 = 3, x 2 = 3 Откуда найдем максимальное значение целевой функции: F(X) = 4*3 + 3*3 = 21

Текущий рекорд Z=22≥ 21, поэтому прекращаем ветвление из этой вершины F(X) = 22, x 1 = 4 x 2 = 2 Дерево решения задачи

Для определения переменной, по которой производится начальное ветвление, разработан ряд правил. • 1. Выбор целочисленной переменной, значение которой в оптимальном решении ЛП-1 имеет наибольшее дробное значение. • 2. Приоритетной является переменная, коэффициент которой в целевой функции превосходит остальные. • 3. Выбор переменной с наименьшим номером. Для дальнейшего ветвления выбираются следующие вершины. • Следует выбирать вершину, соответствующую наибольшему оптимальному значению целевой функции. • Произвольнымвершина является прозондированной в том случае, если она удовлетворяет хотя бы одному из следующих образом выбирается задача ЛП, решавшаяся последней. Промежуточная условий • 1. Оптимальное решение, соответствующее данной вершине целочисленно. • 2. Задача ЛП, соответствующая рассмотренной вершине, не имеет допустимых решений. • 3. Оптимальное значение f (x) соответствующей задачи ЛП не превосходит текущей нижней границы. При использовании метода ветвей и границ выбор вершины для дальнейшего ветвления происходит до тех пор, пока остаётся хотя бы одна не прозондированная вершина. Прозондированная вершина с наилучшим значением f (x) даёт оптимальное решение исходной задачи ЦЛП. Получение перед реализацией метода ветвей и границ допустимого целочисленного решения задачи ЦЛП может оказаться весьма полезным, так как оно даёт начальную нижнюю границу, используемую до получения лучшей нижней границы по методу ветвей и границ. Анализ опыта решения практических задач привёл к выработке ряда рекомендаций который можно использовать для уменьшения времени вычислений. • 1. Количество целочисленных переменных следует уменьшить насколько возможно. Например, целочисленные переменные, значения которых должны быть не меньше 20, можно рассматривать как непрерывные. • 2. Добавление новых ограничений, особенно включающих целочисленные переменные, обычно уменьшает время решения задач ЦЛП. • 3. По возможности следует получать близкие друг к другу верхнюю и нижнюю границы значений целочисленных переменных. • 4. Можно заканчивать реализацию метода ветвей и границ, если для задач максимизации выполняется соотношение: . • 5. Рекомендуется выбирать для ветвления целочисленные переменные в порядке убывания их приоритета, назначаемого в соответствии с технико - экономической интерпретацией переменных и опытом пользователя. В задачах с большим количеством переменных более эффективным является метод отсечения Гомори, который основан на введении дополнительных условий и анализе значений базисных и небазисных переменных , т. е. выполняется модифицированный симплекс-метод. Кроме того, данный метод может применяться в параметрическом программировании, когда исходные данные (коэффициенты) в ЦФ и ограничениях являются не постоянными величинами, а функциями, зависящими определенным образом от некоторых параметров.

Задача № 2 не имеет допустимых значений