47507.ppt
- Количество слайдов: 179

Зачем нужно строить асимптоты графиков дробно-рациональной функции? ©Кожин Дмитрий, Спиридонов Александр

«Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это — построение графиков—является средством увидеть формулы и функции и проследить, каким образом эти функции меняются» . И. М. Гельфанд, основатель и руководитель ВЗМШ, один из крупнейших математиков XX века
1. Асимптоты – ориентир для построения графиков

Проблемный вопрос: Нельзя ли с первого взгляда определить, какие асимптоты имеют график и сколько их, можно ли найти уравнения асимптот элементарными методами? 4

При исследовании поведения функции на бесконечных ветвях (т. е при х→∞ и при х→-∞) и вблизи точек разрыва часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называются асимптотами. 5

Определение асимптоты Асимптотой кривой называется прямая, к которой приближаются как угодно близко точки кривой по мере их удаления в бесконечность. [Алгебра. 9 класс: учебник для общеобразовательных учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - М. : Просвещение, 2009. – 271 с. ] 6

Определение асимптоты Аси мптота (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, к которой эта ветвь неограниченно приближается. [Википедия: ru. wikipedia. org] 7

Определение асимптоты Прямая y= kx+b называется асимптотой y= f(x), если [Курс математики для техникумов под редакцией Матвеева Н. М. / Москва, «Наука» 1977 г. ] 8

Определение асимптоты Под асимптотой подразумевается такая линия, которая, будучи неопределенно продолжена, приближается к данной кривой или к некоторой ее части так, что расстояние между обеими линиями делается менее всякой данной величины. [ Большой энциклопедический словарь Брокгауза Ф. А. , Ефрона И. А. , http: //www. cultinfo/ru/fultext/1/007/121] 9

Определение асимптоты Асимптота – прямая, к которой неограниченно приближается точка, движущаяся по графику, неограниченно удаляясь от начала координат. [Мышкис А. Д. , Сатьянов П. Г. Функции и графики, с. 248 /Факультативный курс по математике: Учебное пособие для 7 -8 кл. сред. шк. / сост. И. Л Никольская, - М. : Просвещение, 1991. -383 с. ] 10

Определение асимптоты Если расстояние от точки М кривой y=f(x) до некоторой определенной прямой при х→х0 и неограниченном удалении точки М от начала координат стремится к нулю, то эта прямая называется асимптотой кривой. [Л. В. Ершов, Р. Б. Райхмист Построение графиков функций: книга для учителя. - М. : Просвещение, 1984. -80 с. ] 11

Определение асимптоты Прямая называется асимптотой графика функции y = f(x), если расстояние переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, то есть точка графика функции при своём стремлении в бесконечность должна неограниченно приближаться к асимптоте. [Википедия: ru. wikipedia. org] 12

Определение асимптоты Асимптота кривой – это прямая, к которой кривая приближается сколь угодно близко при удалении в бесконечность. [Энциклопедический словарь юного математика /Сост. А. П. Савин. М. : Педагогика, 1989. -352 с. ] 13

Определение асимптоты Некоторые определения несколько не совпадают с приведёнными ранее [Н. О. Вирченко, И. И. Ляшко, К. И. Швецов Графики функций. Справочник. Киев, «Наукова думка» , 1977] Асимптота (геометр. ) — прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Асимптота — прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, но никогда не пересекает её, так что расстояние между ними делается бесконечно малой величиной. Нетрудно заметить, что последние два определения исключают случаи, когда кривая пересекает асимптоту. 14

Для графиков каких функций нужно строить асимптоты? 15

Что нам известно об особенности графика функции Если k>0, при неограниченном возрастании положительных значений аргумента значения функции, оставаясь положительными убывают и стремятся к нулю, т. е. если x>0 и x→+∞, то у → 0. Аналогично, если x<0 и x→ - ∞, то у → 0. На графике это свойство проявляется в том, что точки графика по мере их удаления в бесконечность (х →±∞) неограниченно приближается к оси абсцисс. Ось х (прямая у=0) является асимптотой графика этой функции. Ось у (прямая х=0) является второй асимптотой графика рассматриваемой функции. Асимптотой кривой называется прямая, к которой приближаются как угодно близко точки кривой по мере их удаления в бесконечность. [ Алгебра. 9 класс: учебник для общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского. - М. : Просвещение, 2009. – 271 с. ] 16
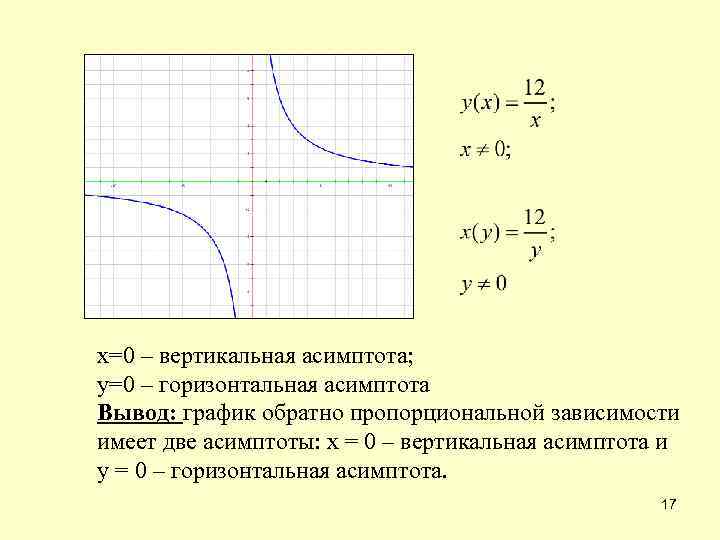
х=0 – вертикальная асимптота; у=0 – горизонтальная асимптота Вывод: график обратно пропорциональной зависимости имеет две асимптоты: х = 0 – вертикальная асимптота и у = 0 – горизонтальная асимптота. 17
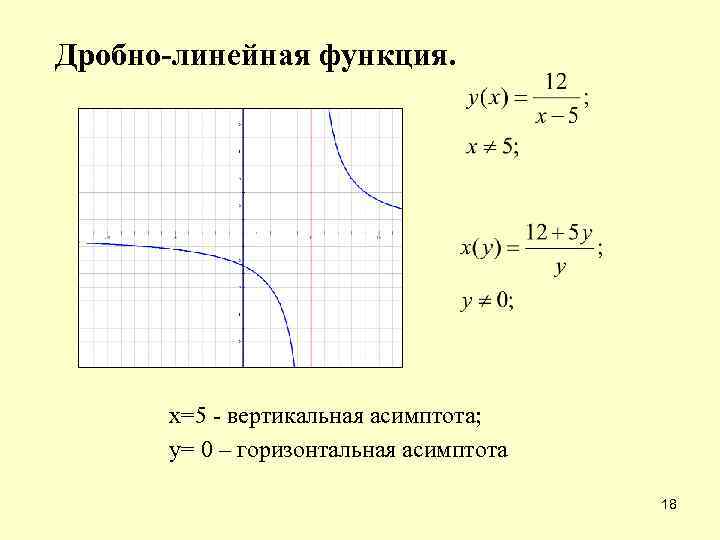
Дробно-линейная функция. х=5 - вертикальная асимптота; у= 0 – горизонтальная асимптота 18
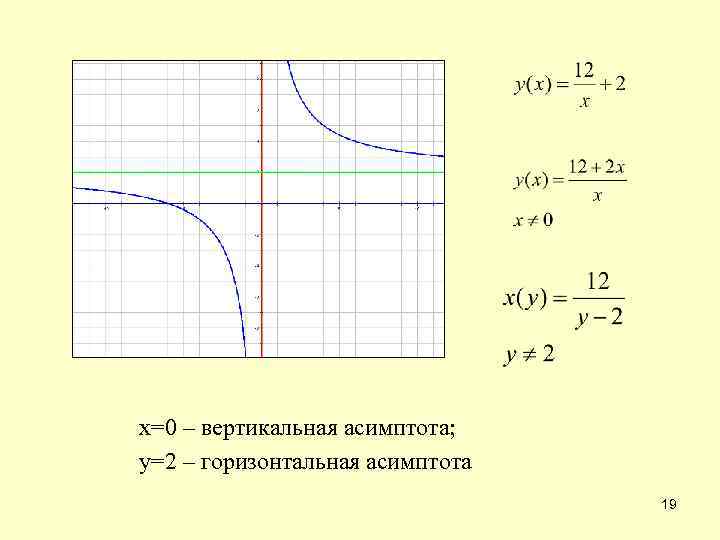
х=0 – вертикальная асимптота; у=2 – горизонтальная асимптота 19
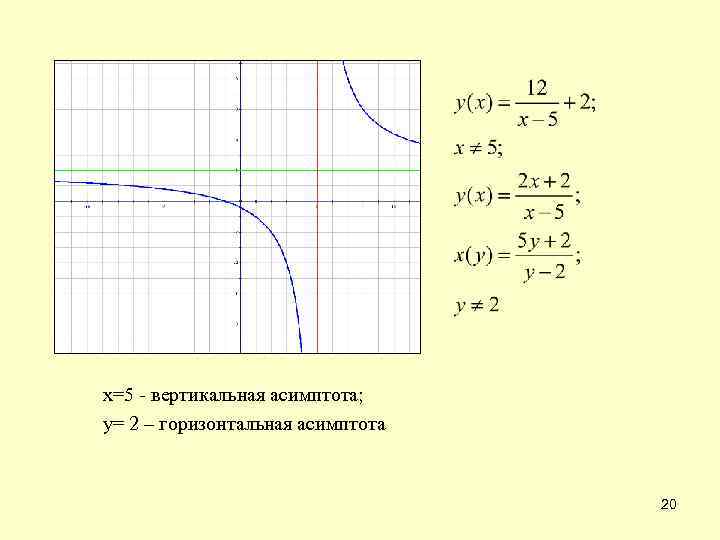
х=5 - вертикальная асимптота; у= 2 – горизонтальная асимптота 20

Определение 1 (определение дробно-линейной функции) Функции, правые части которых – дроби, у которых числитель многочлен первой степени или число отличное от нуля, а знаменатель – многочлен первой степени, называются дробно – линейными функциями. [Алгебра. 9 класс: учебник для общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского. - М. : Просвещение, 2009. – 271 с. ] 21

Определение 2 (определение дробно-линейной функции) Дробно – линейной функцией называется функции, которую можно задать формулой вида где х – переменная, a, b, c, d – произвольные числа, причем c≠ 0 и ad - bc ≠ 0. [ Алгебра. 9 класс: учебник для общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского. - М. : Просвещение, 2009. – 271 с. ] 22

Ограничения, что c≠ 0 и ad - bc ≠ 0 существенны. Если с=0, то получится линейная функция Если ad - bc = 0, то получится сократимая дробь, значение которой равно b/d. [ Алгебра. 9 класс: учебник для общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского. - М. : Просвещение, 2009. – 271 с. ] 23

Если ad – bc = 0, ; d≠ 0, иначе bc=0 →b=0, т. к. по определению дробно - рациональной функции с≠ 0, то b=0. Тогда: 24
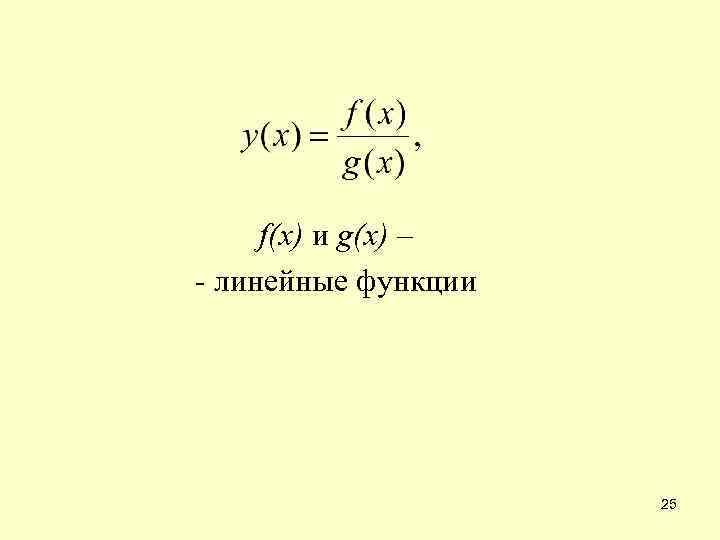
f(x) и g(x) – - линейные функции 25
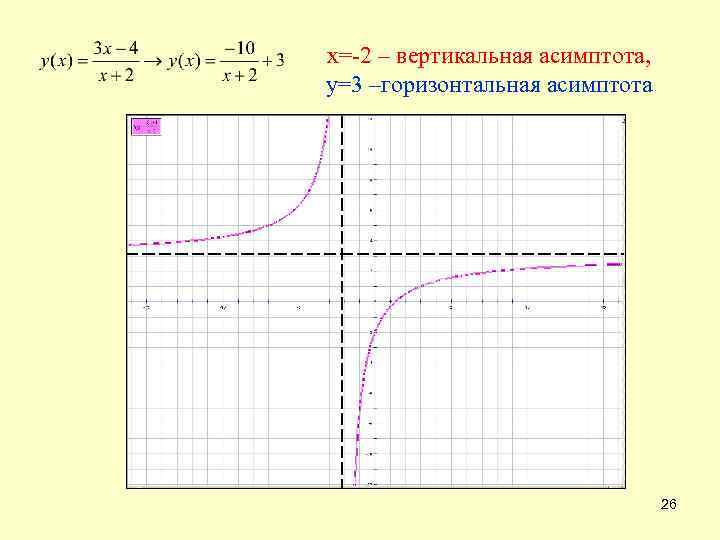
х=-2 – вертикальная асимптота, у=3 –горизонтальная асимптота 26
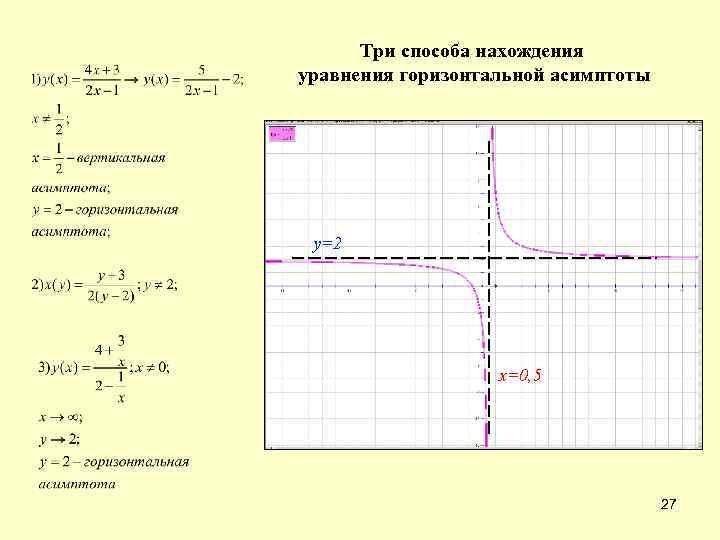
Три способа нахождения уравнения горизонтальной асимптоты у=2 х=0, 5 27

График дробно-линейной функции имеет две асимптоты: вертикальную x = А и горизонтальную y = В. Чтобы найти значение А, надо знаменатель приравнять к нулю и решить полученное линейное уравнение. Найти значение В, можно тремя способами: 1) надо числитель разделить на знаменатель. При делении получается const(В) + остаток; В= const; 2) надо х выразить через у, знаменатель полученной дроби приравнять к нулю и решить полученное уравнение; 3) Надо числитель и знаменатель разделить на х и определить к какому числу стремится у при стремлении х к ±∞. 28

29

• График дробно-линейной функции имеет две асимптоты: вертикальную и горизонтальную. • Уравнение вертикальной асимптоты • Уравнение горизонтальной асимптоты 30

Дробно – рациональная функция и асимптоты ее графика 31
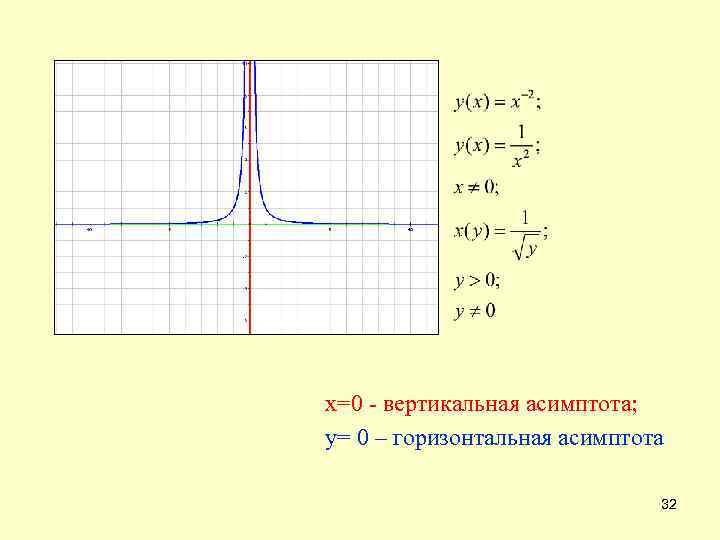
х=0 - вертикальная асимптота; у= 0 – горизонтальная асимптота 32
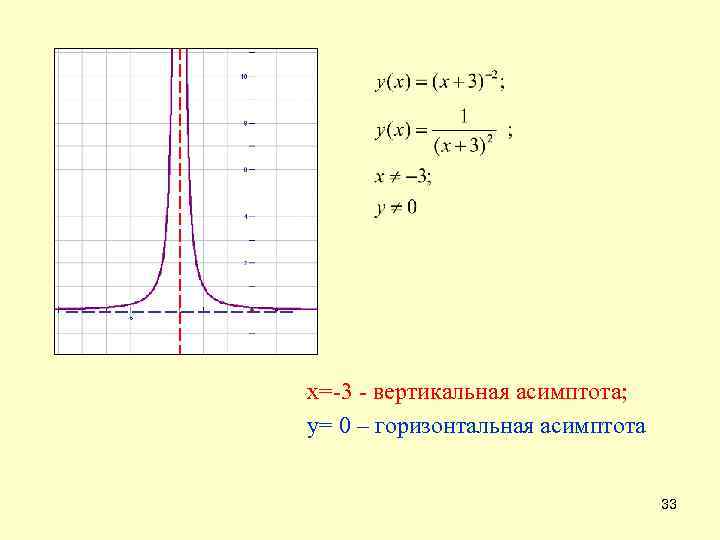
х=-3 - вертикальная асимптота; у= 0 – горизонтальная асимптота 33
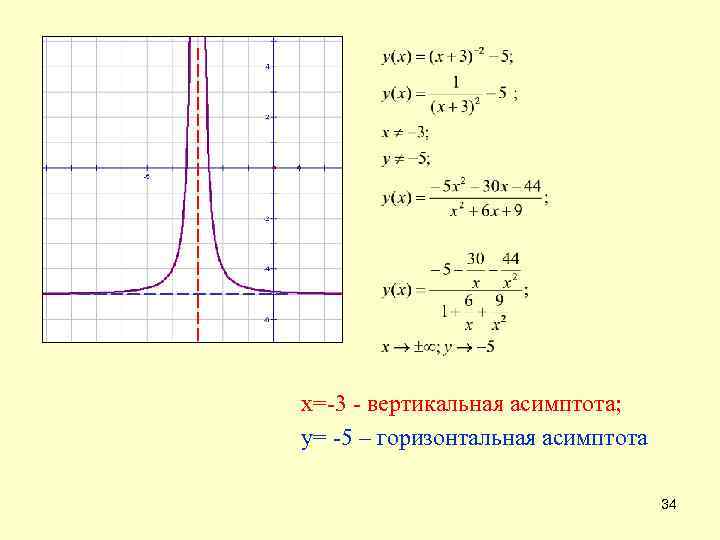
х=-3 - вертикальная асимптота; у= -5 – горизонтальная асимптота 34

В числителе и знаменателе дроби в правой части многочлены второй степени. Такую функцию называют дробно-рациональной. Определение 1. Дробно-рациональной функцией называется дробь, числителем и знаменателем которой являются многочлены. 35

Определение 2 (определение дробно-рациональной функции) Функция вида , где f(x) и g(x) – - алгебраические функции, называется дробно рациональной функцией. [Литинский Г. И. Функции и графики , -М. : Аслан, 1995. -192 с. ] 36

Изучению асимптот помогает «Живая геометрия» 37
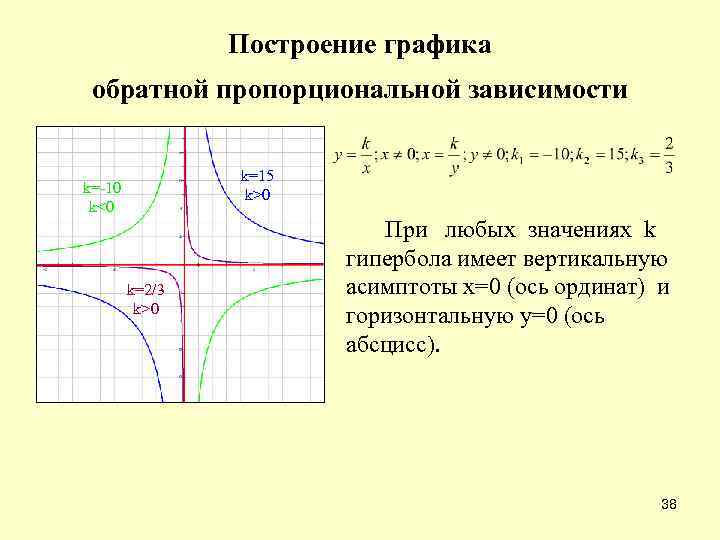
Построение графика обратной пропорциональной зависимости k=15 k>0 k=-10 k<0 k=2/3 k>0 При любых значениях k гипербола имеет вертикальную асимптоты х=0 (ось ординат) и горизонтальную у=0 (ось абсцисс). 38
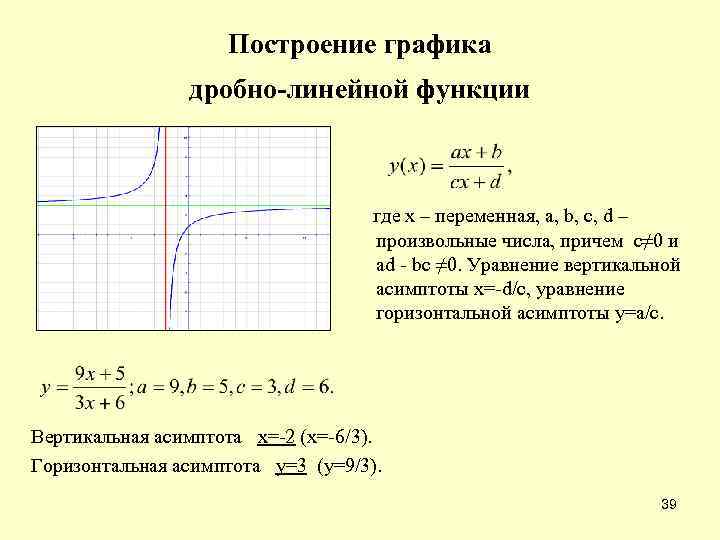
Построение графика дробно-линейной функции где х – переменная, a, b, c, d – произвольные числа, причем c≠ 0 и ad - bc ≠ 0. Уравнение вертикальной асимптоты x=-d/c, уравнение горизонтальной асимптоты y=a/c. Вертикальная асимптота х=-2 (х=-6/3). Горизонтальная асимптота у=3 (у=9/3). 39

Построение графика дробно - рациональной функции Мы будем рассматривать такие ситуации, когда степени числителя и знаменателя не превосходят двух. 40
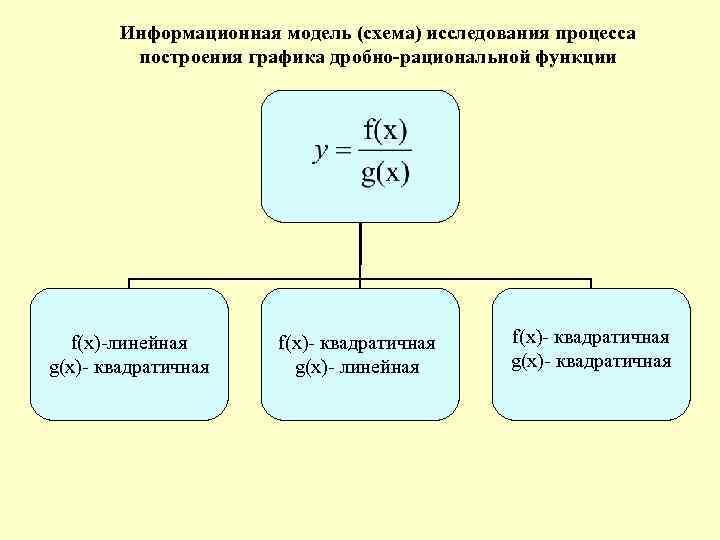
Информационная модель (схема) исследования процесса построения графика дробно-рациональной функции f(x)-линейная g(x)- квадратичная f(x)- квадратичная g(x)- линейная f(x)- квадратичная g(x)- квадратичная
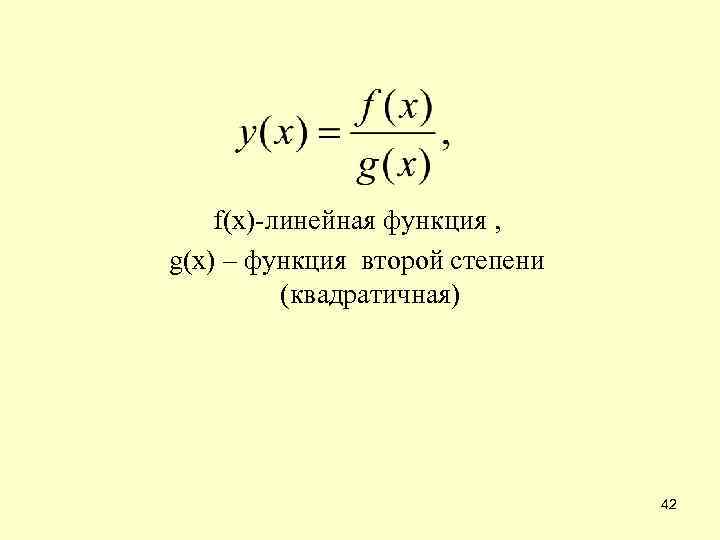
f(x)-линейная функция , g(x) – функция второй степени (квадратичная) 42
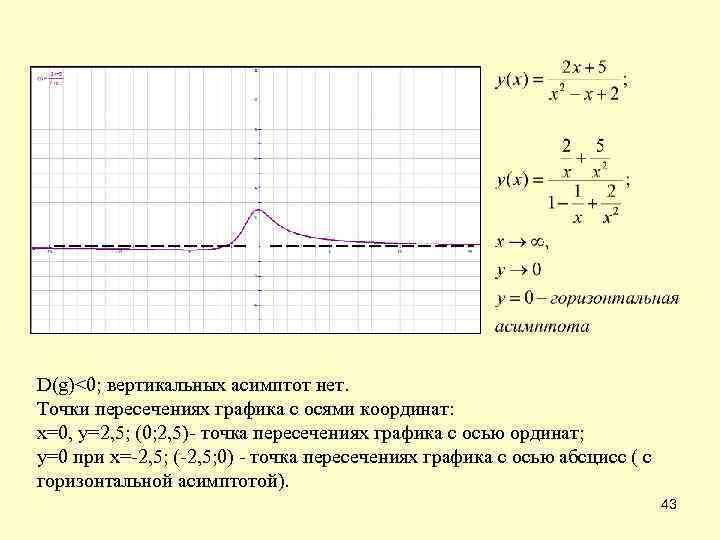
D(g)<0; вертикальных асимптот нет. Точки пересечениях графика с осями координат: х=0, у=2, 5; (0; 2, 5)- точка пересечениях графика с осью ординат; у=0 при х=-2, 5; (-2, 5; 0) - точка пересечениях графика с осью абсцисс ( с горизонтальной асимптотой). 43
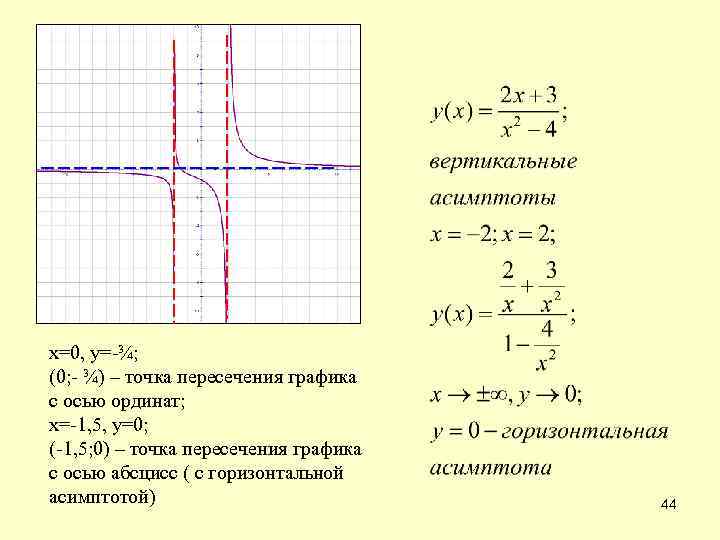
х=0, у=-¾; (0; - ¾) – точка пересечения графика с осью ординат; х=-1, 5, у=0; (-1, 5; 0) – точка пересечения графика с осью абсцисс ( с горизонтальной асимптотой) 44
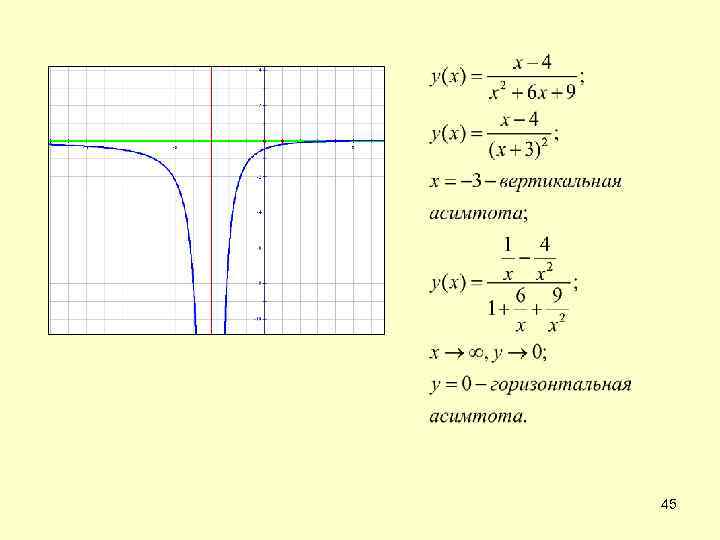
45
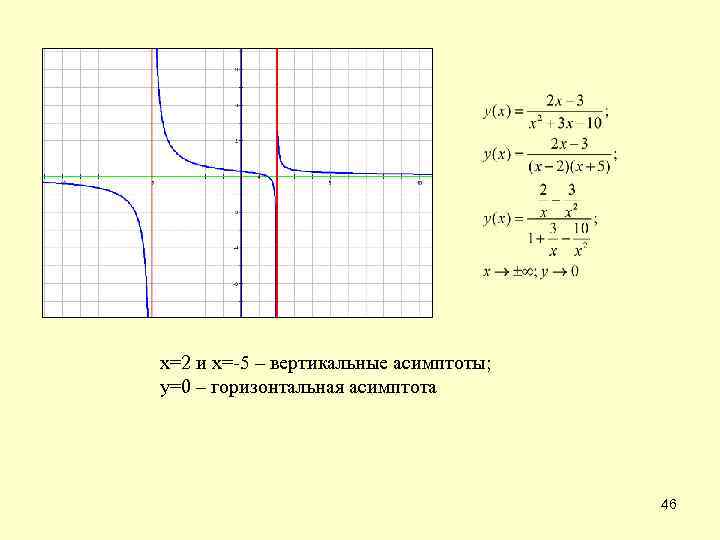
х=2 и х=-5 – вертикальные асимптоты; у=0 – горизонтальная асимптота 46
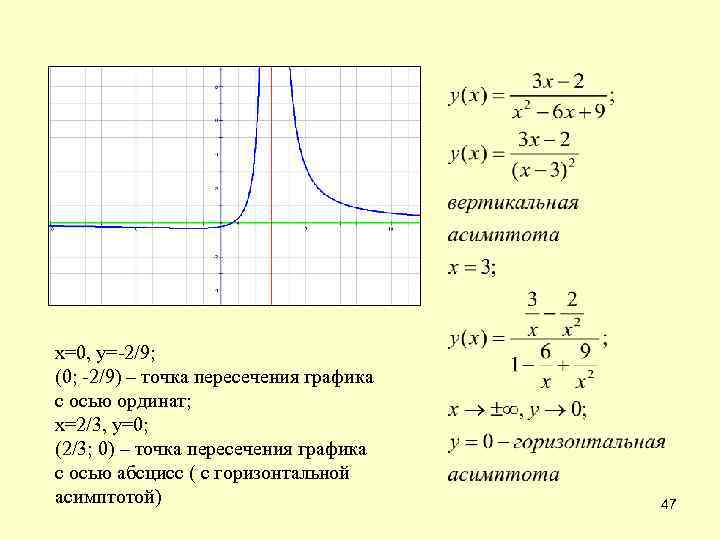
х=0, у=-2/9; (0; -2/9) – точка пересечения графика с осью ординат; х=2/3, у=0; (2/3; 0) – точка пересечения графика с осью абсцисс ( с горизонтальной асимптотой) 47
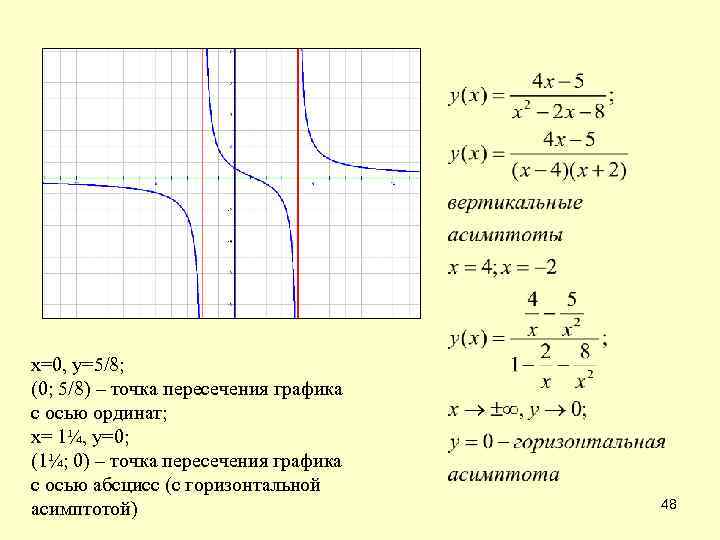
х=0, у=5/8; (0; 5/8) – точка пересечения графика с осью ординат; х= 1¼, у=0; (1¼; 0) – точка пересечения графика с осью абсцисс (с горизонтальной асимптотой) 48

Если числитель дробно - рациональной функции у(x) линейная функция, а знаменатель – функция второй степени (квадратичная), то график данной функции имеет горизонтальную асимптоту (ось абсцисс), которую пересекает в одной точке, и может иметь не более двух вертикальных асимптот. 49
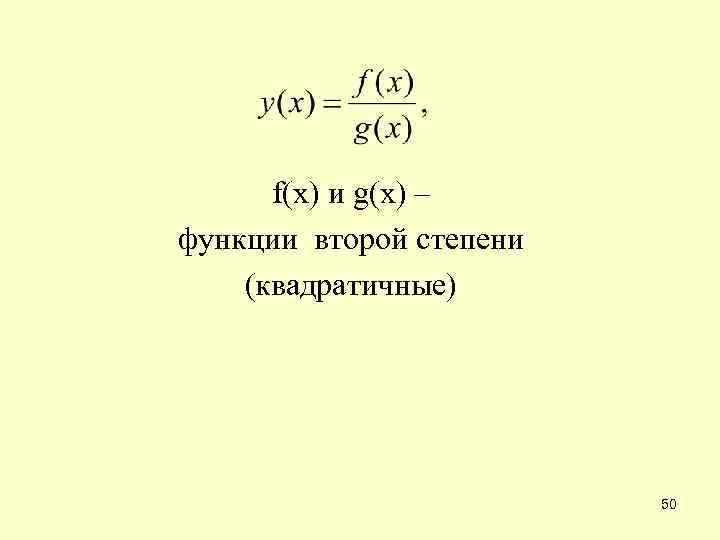
f(x) и g(x) – функции второй степени (квадратичные) 50
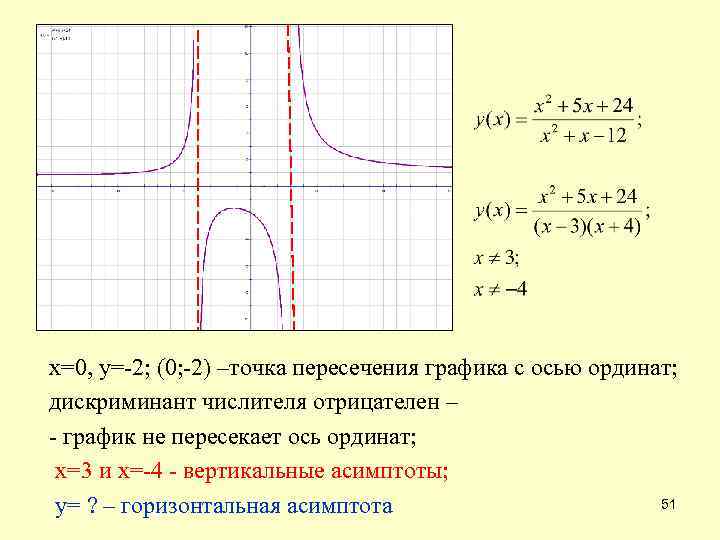
х=0, у=-2; (0; -2) –точка пересечения графика с осью ординат; дискриминант числителя отрицателен – - график не пересекает ось ординат; х=3 и х=-4 - вертикальные асимптоты; 51 у= ? – горизонтальная асимптота
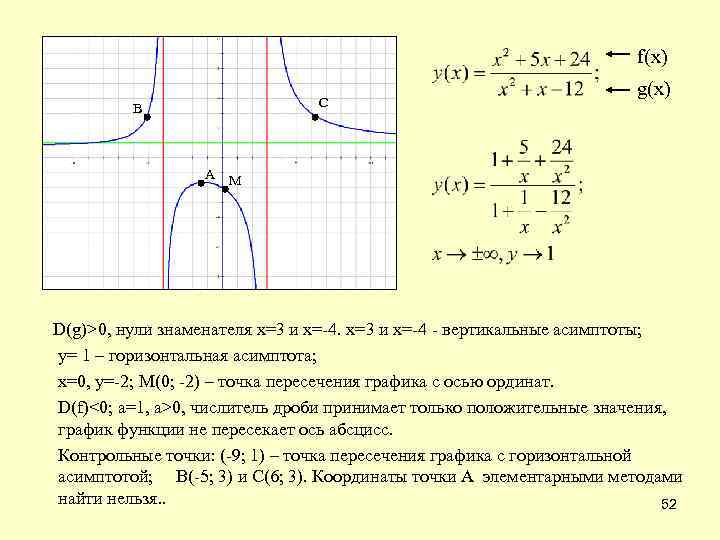
f(x) С В g(x) А М А D(g)>0, нули знаменателя х=3 и х=-4 - вертикальные асимптоты; у= 1 – горизонтальная асимптота; х=0, у=-2; М(0; -2) – точка пересечения графика с осью ординат. D(f)<0; а=1, a>0, числитель дроби принимает только положительные значения, график функции не пересекает ось абсцисс. Контрольные точки: (-9; 1) – точка пересечения графика с горизонтальной асимптотой; В(-5; 3) и С(6; 3). Координаты точки А элементарными методами найти нельзя. . 52
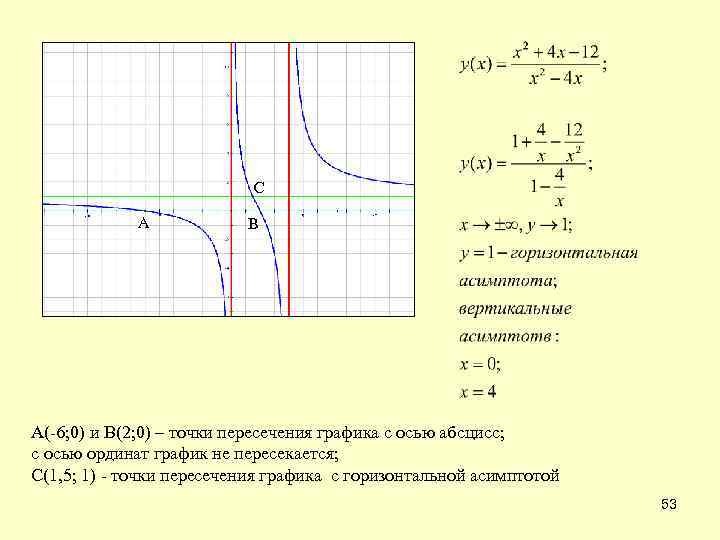
С А В А(-6; 0) и В(2; 0) – точки пересечения графика с осью абсцисс; с осью ординат график не пересекается; С(1, 5; 1) - точки пересечения графика с горизонтальной асимптотой 53
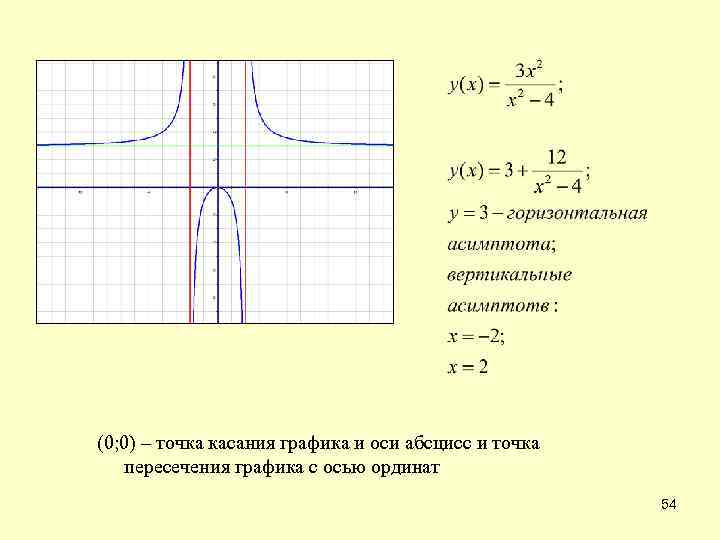
(0; 0) – точка касания графика и оси абсцисс и точка пересечения графика с осью ординат 54
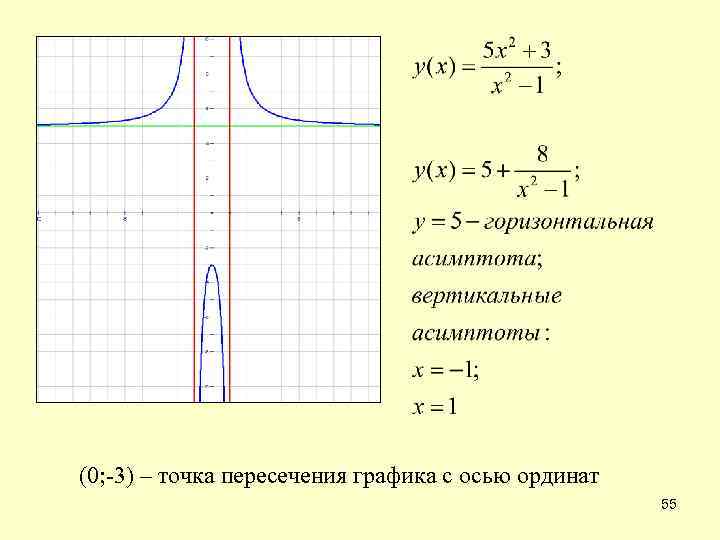
(0; -3) – точка пересечения графика с осью ординат 55
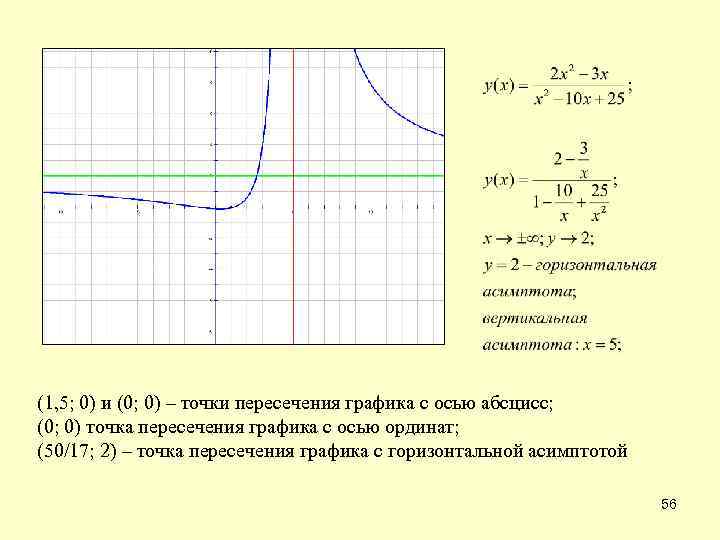
(1, 5; 0) и (0; 0) – точки пересечения графика с осью абсцисс; (0; 0) точка пересечения графика с осью ординат; (50/17; 2) – точка пересечения графика с горизонтальной асимптотой 56
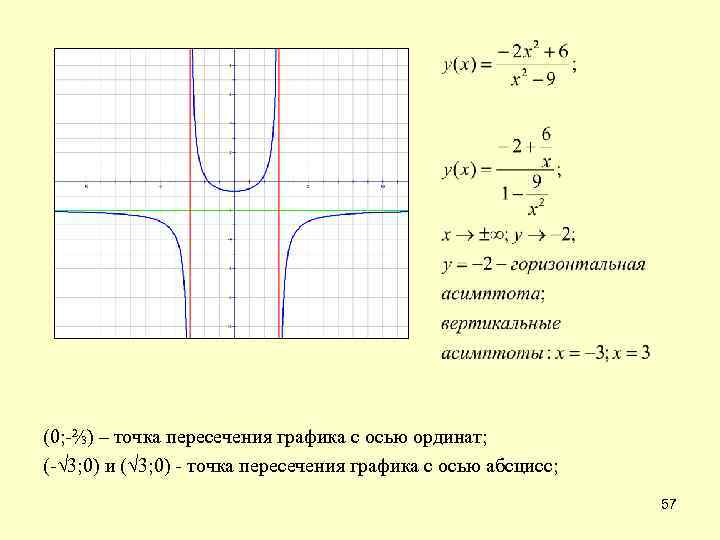
(0; -⅔) – точка пересечения графика с осью ординат; (-√ 3; 0) и (√ 3; 0) - точка пересечения графика с осью абсцисс; 57
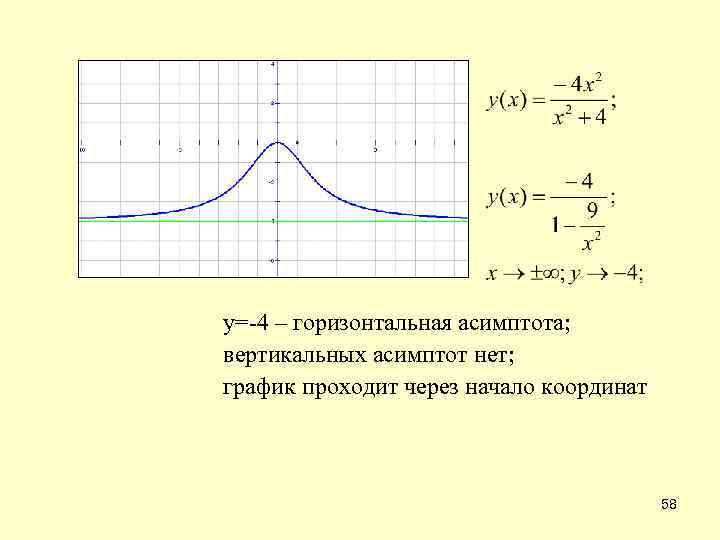
у=-4 – горизонтальная асимптота; вертикальных асимптот нет; график проходит через начало координат 58
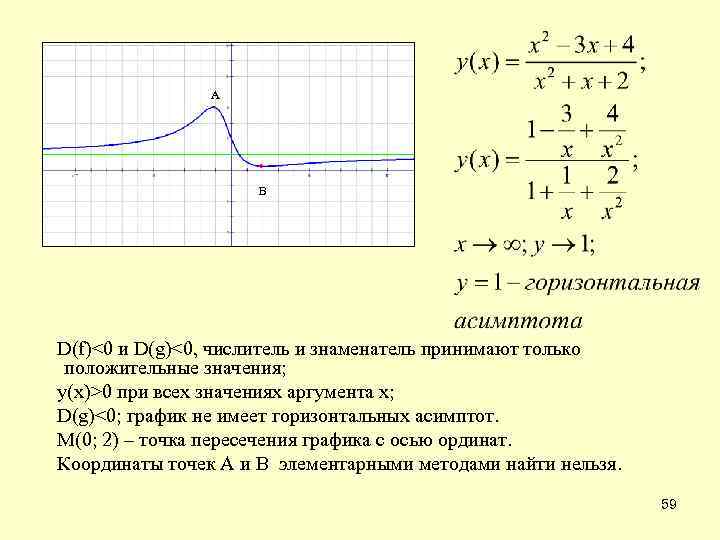
А А А ВВ D(f)<0 и D(g)<0, числитель и знаменатель принимают только положительные значения; у(х)>0 при всех значениях аргумента х; D(g)<0; график не имеет горизонтальных асимптот. М(0; 2) – точка пересечения графика с осью ординат. Координаты точек А и В элементарными методами найти нельзя. 59
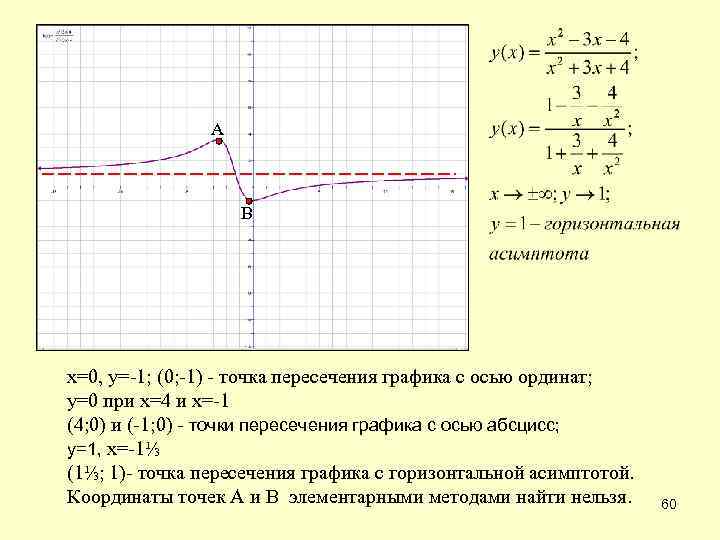
А В х=0, у=-1; (0; -1) - точка пересечения графика с осью ординат; у=0 при х=4 и х=-1 (4; 0) и (-1; 0) - точки пересечения графика с осью абсцисс; у=1, х=-1⅓ (1⅓; 1)- точка пересечения графика с горизонтальной асимптотой. Координаты точек А и В элементарными методами найти нельзя. 60

График дробно-рациональной функции, у которой числитель и знаменатель второй степени, имеет горизонтальную асимптоту у = В (В≠ 0) и может иметь две вертикальных асимптоты, если дискриминант знаменателя положителен, одну вертикальную асимптоту, если дискриминант знаменателя равен нулю, или не имеет ни одной асимптоты, если дискриминант знаменателя отрицателен. График дробно-рациональной функции может пересекать горизонтальную асимптоту. 61
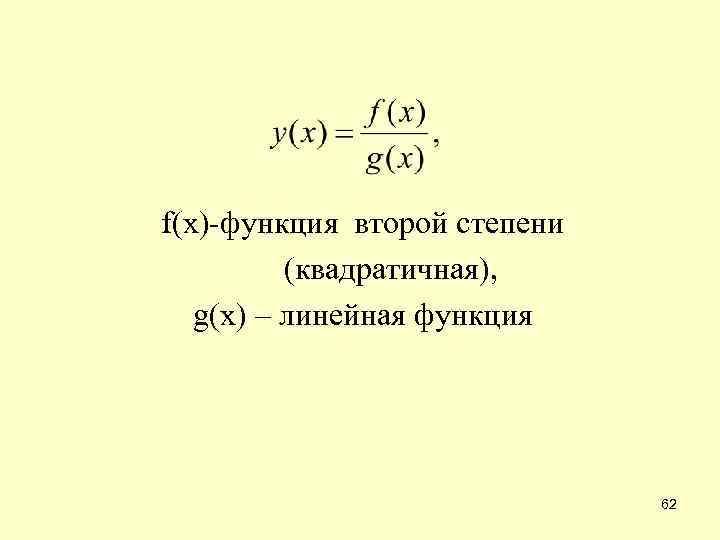
f(x)-функция второй степени (квадратичная), g(x) – линейная функция 62
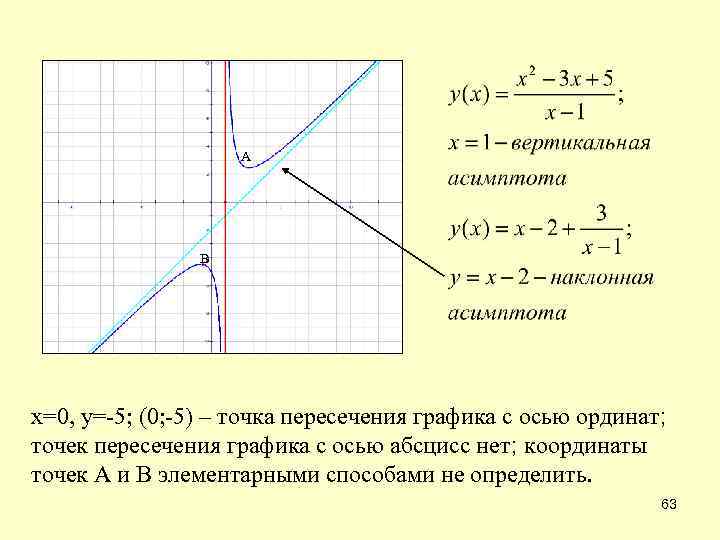
А В х=0, у=-5; (0; -5) – точка пересечения графика с осью ординат; точек пересечения графика с осью абсцисс нет; координаты точек А и В элементарными способами не определить. 63
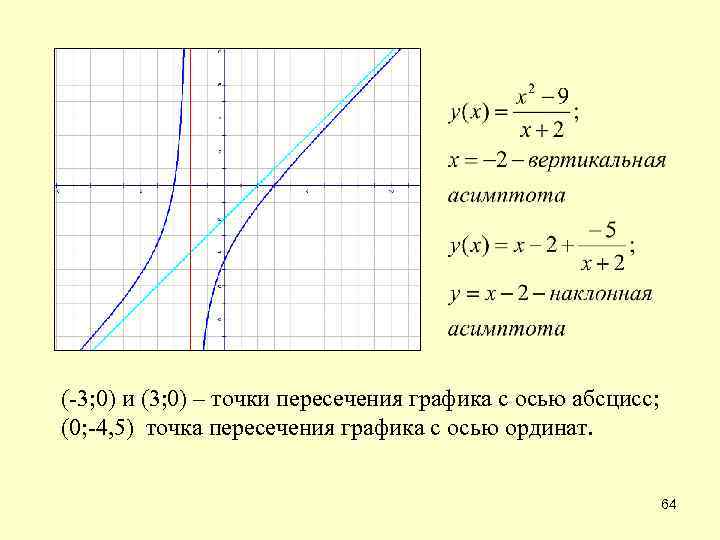
(-3; 0) и (3; 0) – точки пересечения графика с осью абсцисс; (0; -4, 5) точка пересечения графика с осью ординат. 64
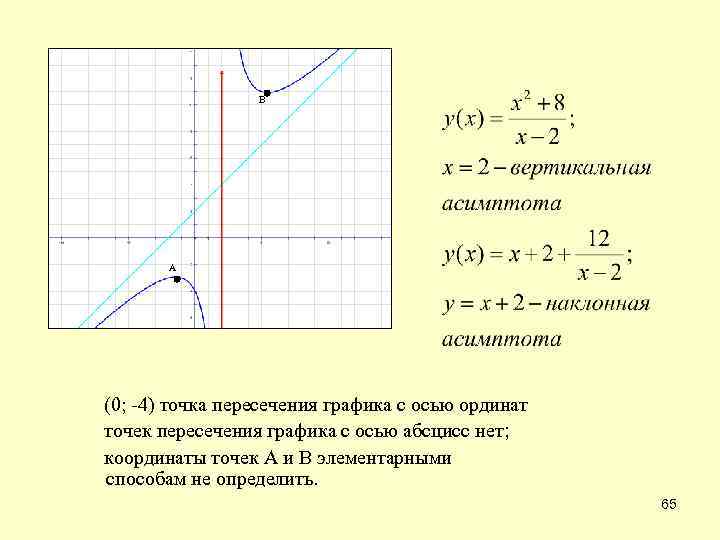
В А (0; -4) точка пересечения графика с осью ординат точек пересечения графика с осью абсцисс нет; координаты точек А и В элементарными способам не определить. 65
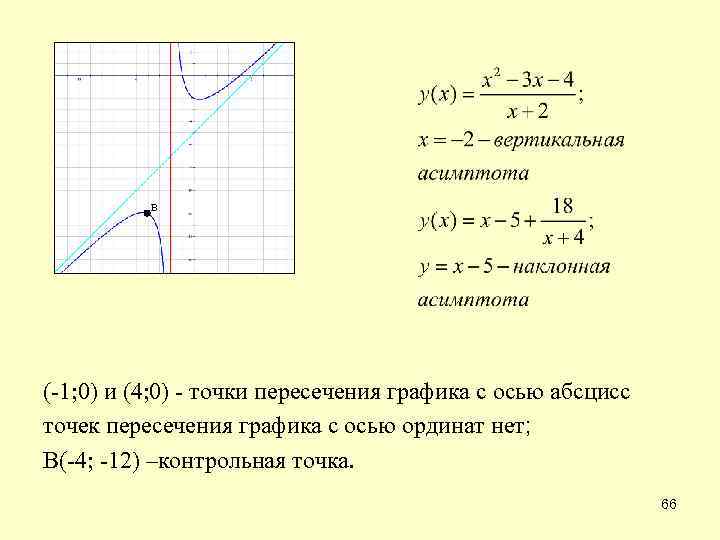
В (-1; 0) и (4; 0) - точки пересечения графика с осью абсцисс точек пересечения графика с осью ординат нет; В(-4; -12) –контрольная точка. 66
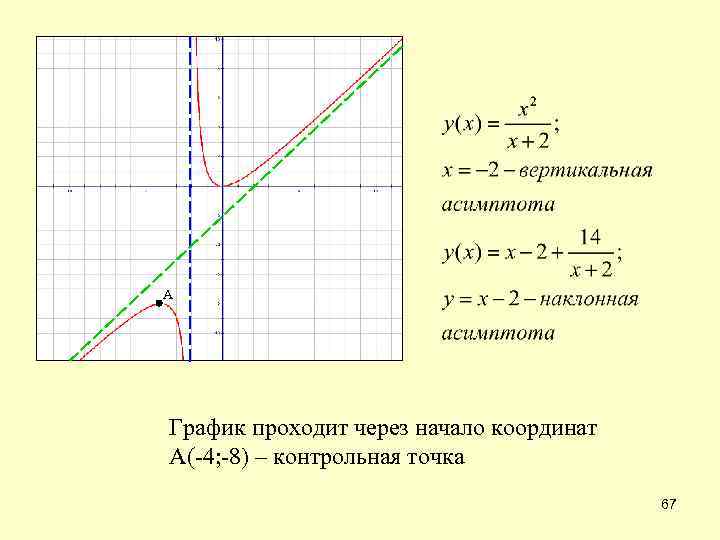
А График проходит через начало координат А(-4; -8) – контрольная точка 67
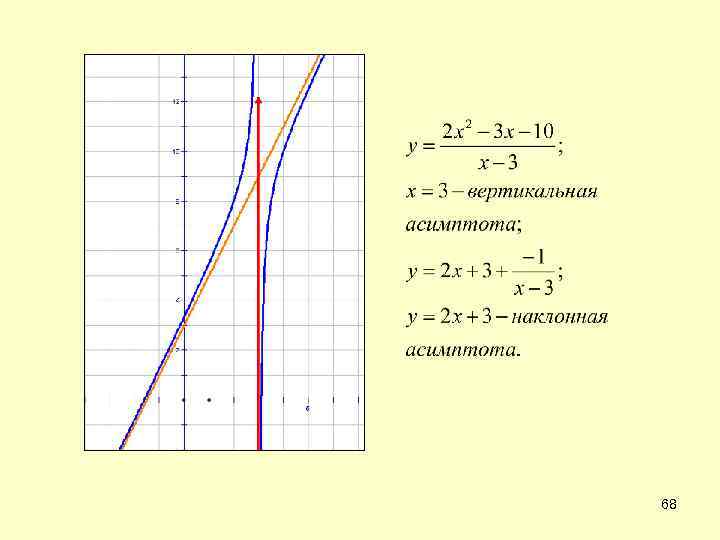
68
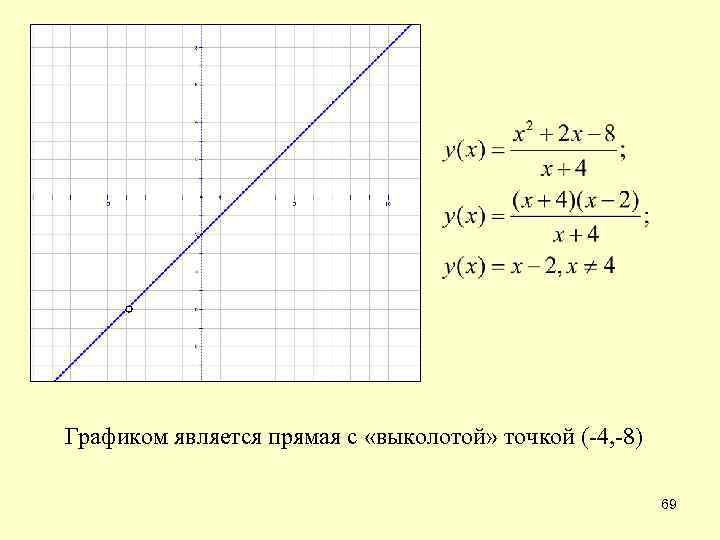
Графиком является прямая с «выколотой» точкой (-4, -8) 69
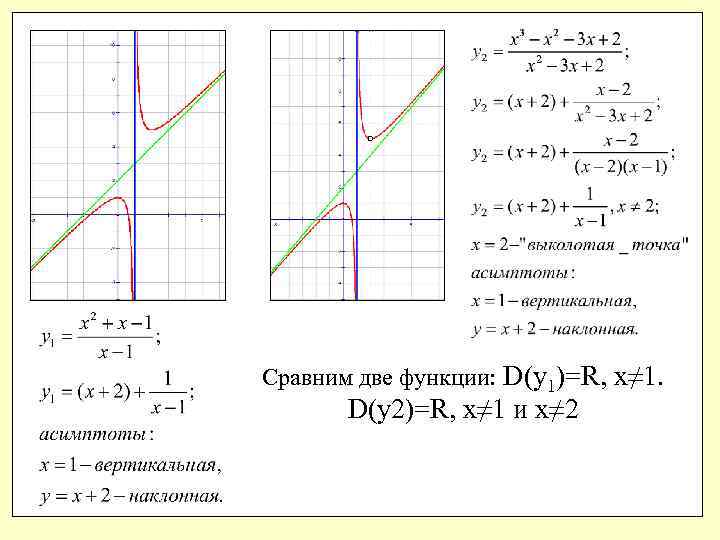
Сравним две функции: D(y 1)=R, x≠ 1. D(y 2)=R, x≠ 1 и x≠ 2

Если числитель дробно-рациональной функции второй степени, знаменатель – линейная функция, то график данной функции имеет наклонную асимптоту – прямую, которая задаётся уравнением у=ax+b, где а≠ 0 и вертикальную асимптоту. 71

• Выполнив работу, мы убедились, что асимптоты действительно являютя ориентиром при построении графика дробно-рациональной функции. • В результате компьютерного моделирования, мы убедились, что эскиз графика дробно-рациональной функции можно строить путём выявления их асимптот и поведения графиков функции при х ±∞ и в точках разрыва функции. • График дробно – рациональной функции, где степени числителя и знаменателя не выше второй степени, может имеет три вида асимптот: вертикальную, горизонтальную и наклонную. • У функции не могут существовать одновременно все три вида асимптот. • Число вертикальных асимптот равно числу нулей знаменателя. • График дробно-рациональной функции (степени числителя и знаменателя не выше второй степени) имеет или только одну наклонную асимптоту, или только одну горизонтальную асимптоту. 72

• График дробно-линейной функции имеет две асимптоты: вертикальную и горизонтальную. • Если числитель дробно - рациональной функции у(x) линейная функция, а знаменатель – квадратичная функция, то график данной функции имеет горизонтальную асимптоту и может иметь не более двух вертикальных асимптот. • График дробно-рациональной функции, у которой числитель и знаменатель второй степени, имеет горизонтальную асимптоту и может иметь не более двух вертикальных асимптот. • Если числитель дробно - рациональной функции квадратичная функция, а знаменатель –линейная функция, то график данной функции имеет наклонную и вертикальную асимптоты. 73

Критерии существования асимптот На основании проведенных компьютерных экспериментов можно установить следующие закономерности и представить их в виде критериев существования асимптот: • Горизонтальные асимптоты существуют у таких функций, у которых степень числителя не превышает степени знаменателя. • Вертикальные асимптоты существуют у таких функций, которые не определены в каких- либо точках. • Наклонные асимптоты существуют у таких функций, у которых степень числителя на единицу превышает степень знаменателя • У графика функции не могут существовать одновременно все три вида асимптот. 74

Возникают вопросы: 1. Существуют ли другие дробно-рациональные которых имеют горизонтальную функции, графики или наклонную асимптоту? 2. Можно ли элементарными способами найти экстремумы дробно-рациональных функций? Это проблемные вопросы будут рассмотрены в дальнейшей работе, т. к. на первом этапе была поставлена цель выявить наличие асимптот графиков дробно-рациональных функций, у которых степень числителя и знаменателя выражения в правой части не выше второй. 75
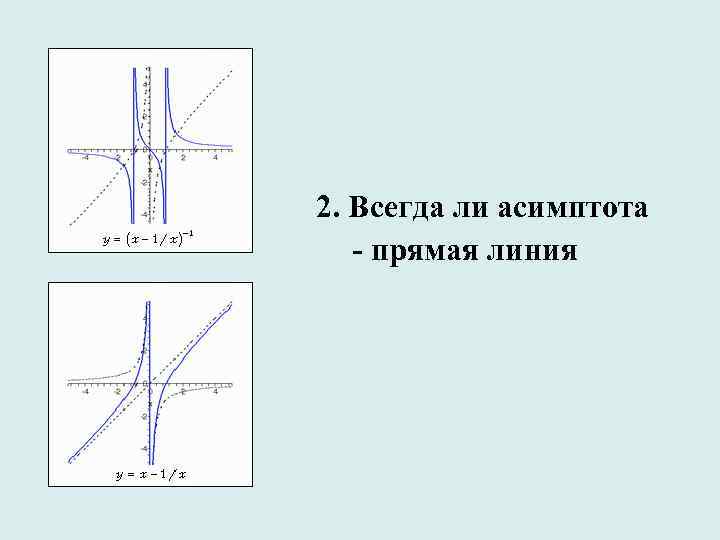
2. Всегда ли асимптота - прямая линия

«Асимптота — прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, так что расстояние между ними делается бесконечно малой величиной» [Википедия ru. wikipedia. org/wiki/Асимптота]. Судя по этому определению, асимптоты могут быть не только прямыми, но и кривыми линиями. Существование криволинейных асимптот показал еще И. Ньютон, а в настоящее время различают асимптоты прямолинейные и криволинейные, но обыкновенно криволинейную асимптоту называют асимптотическою кривою.

Исследование дробно-рациональных функций, у которых числитель и знаменатель являются многочленами не выше второй степени, показало, что все асимптоты графиков таких функций являются прямыми линиями. Теперь в своем исследовании мы будем искать асимптоты, являющиеся кривыми линиями среди графиков функций, степень числителя и знаменателя которых выше второй.

В книге Шахмейстера А. Х. «Построение графиков функций элементарными методами» предлагаются задачи на исследование функций построение графиков, решение которых автор дает на основании понятия предела функции.

• В основу своего исследования мы положили следующие проблемные вопросы: «Всегда ли асимптота графика дробно-рациональной функции является прямой линией? Может ли асимптотой графика дробно-рациональной функции быть парабола или гипербола? Как найти уравнения таких линий элементарными методами? » • Объект исследования: графики дробно-рациональной функции, у которых степени числителя и знаменателя не ниже второй. • Предмет исследования: вид асимптот. • Цель исследования: выяснить, какие асимптоты имеют графики дробно-рациональных функций при условии, что степени числителя и знаменателя дроби в правой части функции выше второй. • Гипотеза: существуют дробно-рациональные функции, графики которых имеют не только вертикальную, горизонтальную или наклонную асимптоты, но и асимптотическую кривую.
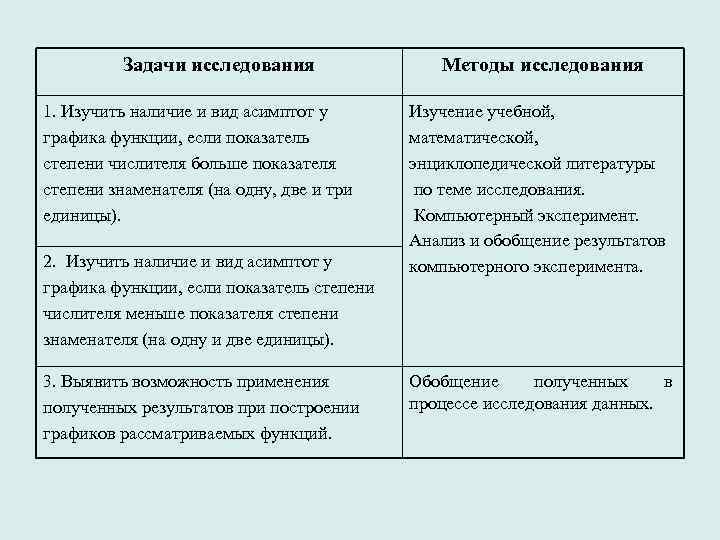
Задачи исследования 1. Изучить наличие и вид асимптот у графика функции, если показатель степени числителя больше показателя степени знаменателя (на одну, две и три единицы). 2. Изучить наличие и вид асимптот у графика функции, если показатель степени числителя меньше показателя степени знаменателя (на одну и две единицы). 3. Выявить возможность применения полученных результатов при построении графиков рассматриваемых функций. Методы исследования Изучение учебной, математической, энциклопедической литературы по теме исследования. Компьютерный эксперимент. Анализ и обобщение результатов компьютерного эксперимента. Обобщение полученных в процессе исследования данных.

-это дробно-линейная функция • График дробно-линейной функции имеет две асимптоты: вертикальную и горизонтальную. • Уравнение вертикальной асимптоты • Уравнение горизонтальной асимптоты

Определение дробно-рациональной функции: Функция вида , где f(x) и g(x) – - алгебраические функции, называется дробно рациональной функцией.

График дробно-линейной функции имеет две асимптоты: вертикальную и горизонтальную. График дробно – рациональной функции, где степени числителя и знаменателя не выше второй степени, может имеет три вида асимптот: вертикальную , горизонтальную и наклонную. У функции не могут существовать одновременно все три вида асимптот.

Если числитель дробно - рациональной функции у(x) линейная функция, а знаменатель – квадратичная функция, то график данной функции имеет горизонтальную асимптоту и может иметь не более двух вертикальных асимптот. График дробно-рациональной функции, у которой числитель и знаменатель второй степени, имеет горизонтальную асимптоту и может иметь не более двух вертикальных асимптот. Если числитель дробно - рациональной функции квадратичная функция, а знаменатель –линейная функция, то график данной функции имеет наклонную и вертикальную асимптоты.

Число вертикальных асимптот графика дробнорациональной функции равно числу нулей знаменателя. График дробно-рациональной функции (степени числителя и знаменателя не выше второй степени) имеет • или только одну наклонную асимптоту, • или только одну горизонтальную асимптоту

Существуют ли другие дробно-рациональные функции, графики которых имеют горизонтальную или наклонную асимптоту?

Во второй части работе изучается вопрос о количестве и виде асимптот дробно-рациональной функции, при условии, что степень числителя и знаменателя дроби в правой части функции не ниже второй. Изучение проводилось при помощи вычислений и компьютерного эксперимента, заключающегося в построении графиков дробнорациональных функций и их асимптот в программе «Живая геометрия» .

Вычисления проводились по следующему правилу: 1. чтобы найти вертикальную асимптоту, нужно знаменатель дроби приравнять к нулю и решить полученное уравнение, т. е. найти нули знаменателя. Так как степень знаменателя не превышает двух, то число нулей знаменателя, а значит, и число вертикальных асимптот не превышает двух; 2. чтобы найти горизонтальную и наклонную асимптоты, нужно выделить целую часть дроби, для чего надо выполнить деление многочлена, стоящего в числителе, на многочлен в знаменателе. Полученное частное и есть уравнение искомой асимптоты.
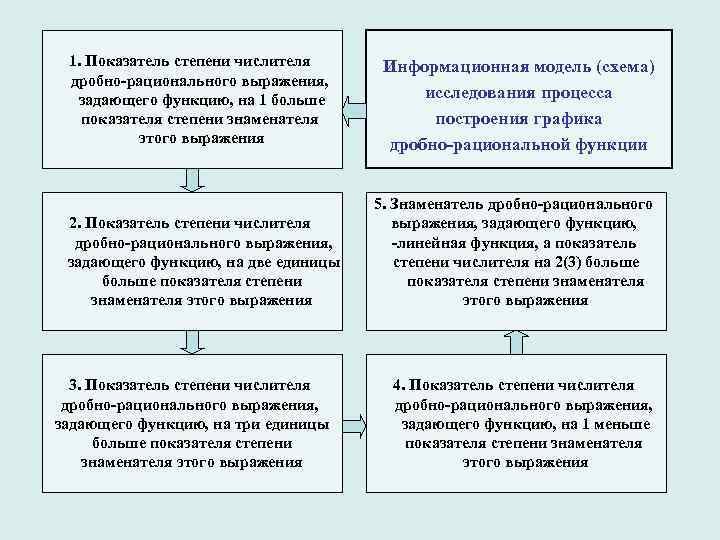
1. Показатель степени числителя дробно-рационального выражения, задающего функцию, на 1 больше показателя степени знаменателя этого выражения 2. Показатель степени числителя дробно-рационального выражения, задающего функцию, на две единицы больше показателя степени знаменателя этого выражения 3. Показатель степени числителя дробно-рационального выражения, задающего функцию, на три единицы больше показателя степени знаменателя этого выражения Информационная модель (схема) исследования процесса построения графика дробно-рациональной функции 5. Знаменатель дробно-рационального выражения, задающего функцию, -линейная функция, а показатель степени числителя на 2(3) больше показателя степени знаменателя этого выражения 4. Показатель степени числителя дробно-рационального выражения, задающего функцию, на 1 меньше показателя степени знаменателя этого выражения

1. Показатель степени числителя дробно-рационального выражения, задающего функцию, на 1 больше показателя степени знаменателя этого выражения
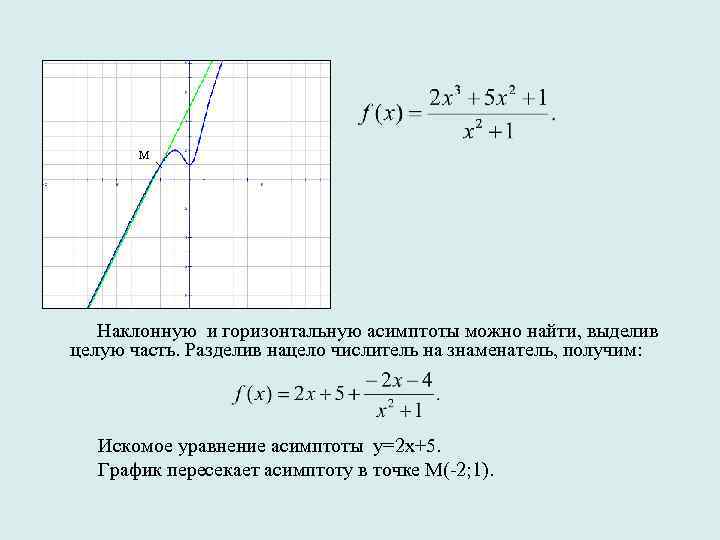
М Наклонную и горизонтальную асимптоты можно найти, выделив целую часть. Разделив нацело числитель на знаменатель, получим: Искомое уравнение асимптоты у=2 х+5. График пересекает асимптоту в точке М(-2; 1).

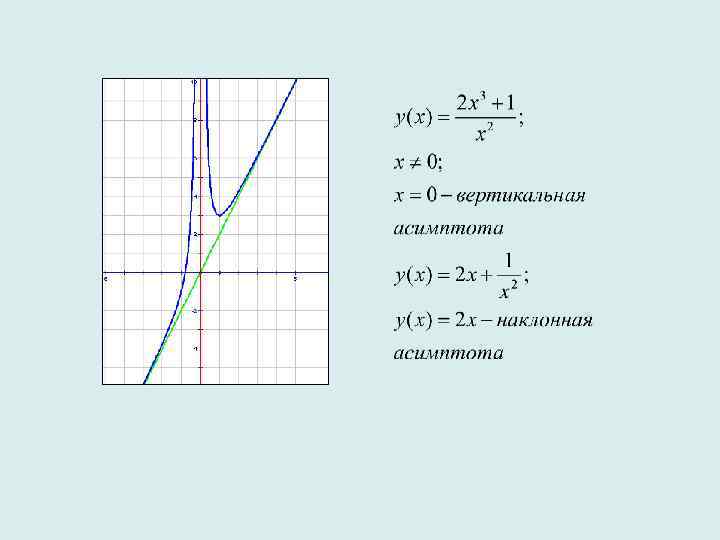
х=-1 – вертикальная асимптота, у=0, 5 х-1 – наклонная асимптота.
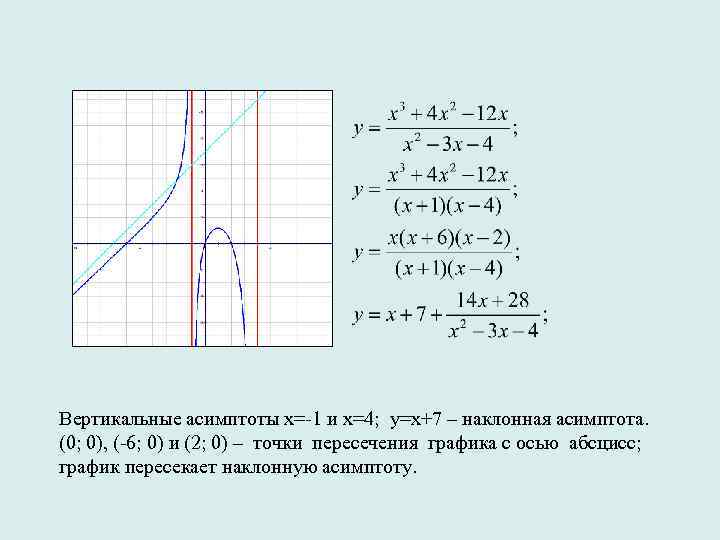
Вертикальные асимптоты х=-1 и х=4; у=х+7 – наклонная асимптота. (0; 0), (-6; 0) и (2; 0) – точки пересечения графика с осью абсцисс; график пересекает наклонную асимптоту.
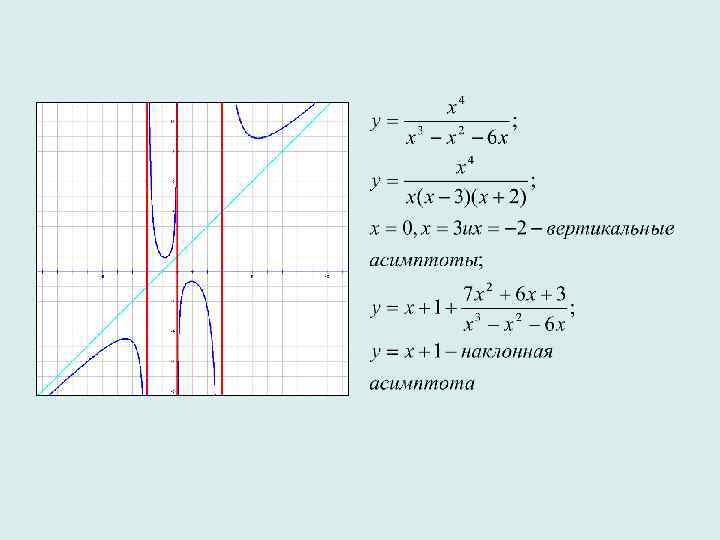

Если показатель степени числителя дробно-рационального выражения, задающего функцию на 1 больше показателя степени знаменателя этого выражения, то график функции может иметь не более одной вертикальной асимптоты и имеет наклонную асимптоту – прямую, которая задаётся уравнением у = ax+b, где а≠ 0.

2. Показатель степени числителя дробно-рационального выражения, задающего функцию, на две единицы больше показателя степени знаменателя этого выражения
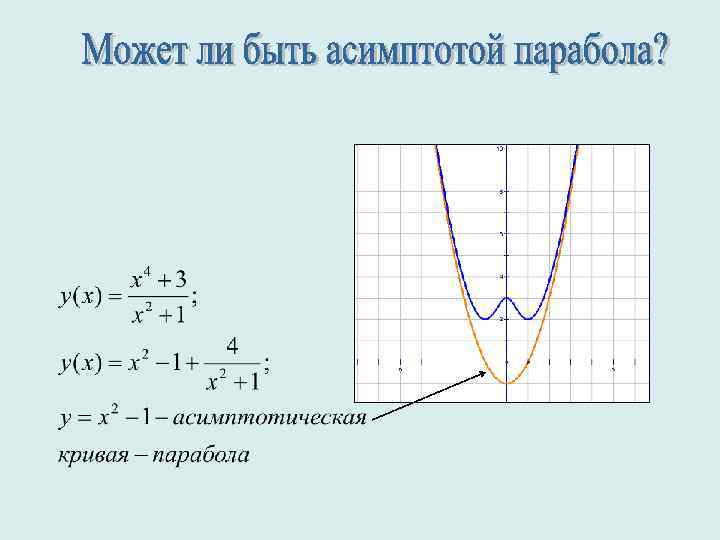

Ныне различают асимптоты прямолинейные и криволинейные, но обыкновенно криволинейную асимптоту называют асимптотическою кривою. Существование криволинейных асимптот, впервые показал Ньютон.
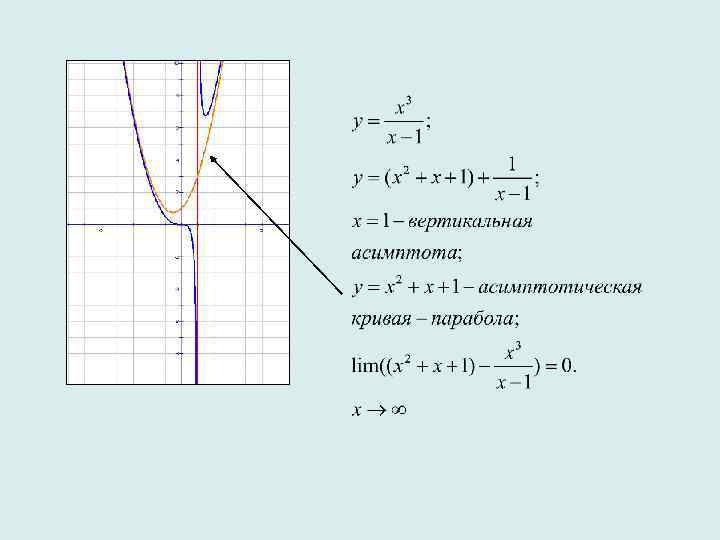
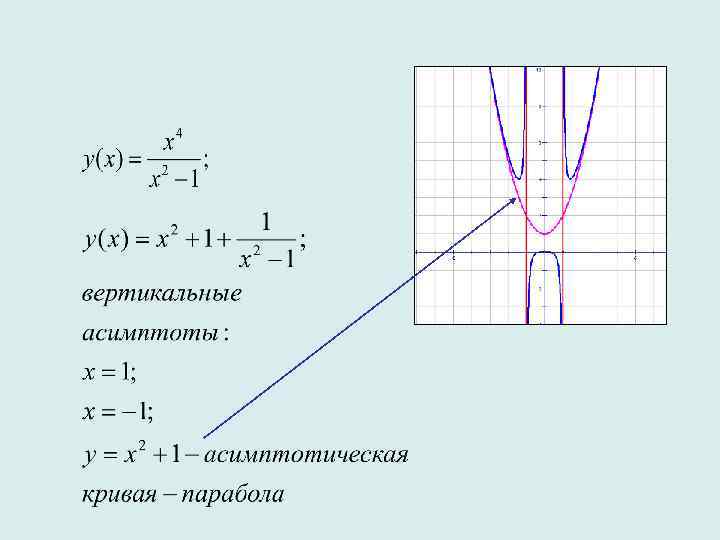

Если показатель степени числителя выражения, задающего функцию, на две единицы больше показателя степени знаменателя этого выражения, то график данной функции имеет асимптотическую кривую - параболу.

3. Показатель степени числителя дробно-рационального выражения, задающего функцию, на три единицы больше показателя степени знаменателя этого выражения
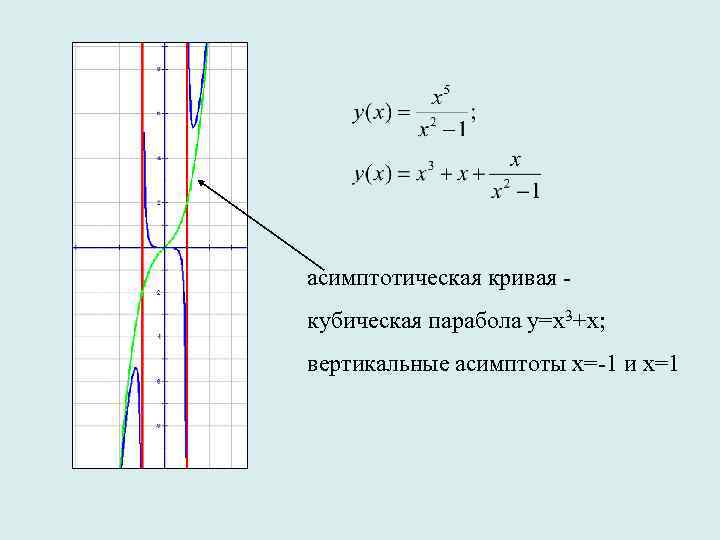
асимптотическая кривая - кубическая парабола у=x 3+x; вертикальные асимптоты х=-1 и х=1

Если у=f(x)/g(x), где n - показатель степени числителя, k - показатель степени знаменателя, n-k равно числу 2, то криволинейная асимптота представляет собой график функции, напоминающий параболу (т. е. у=x 2). Если n-k равно 3, то асимптотой служит график, сходный с графиком функции у=x 3, т. е. с кубической параболой.

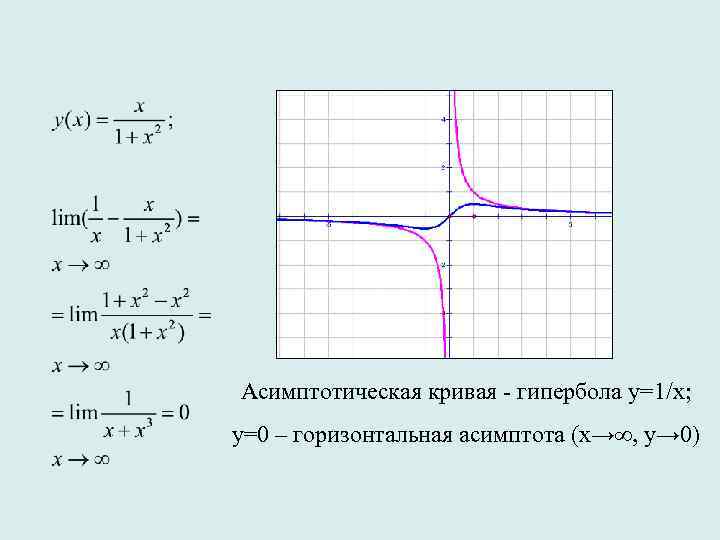
Асимптотическая кривая - гипербола у=1/x; у=0 – горизонтальная асимптота (х→∞, у→ 0)
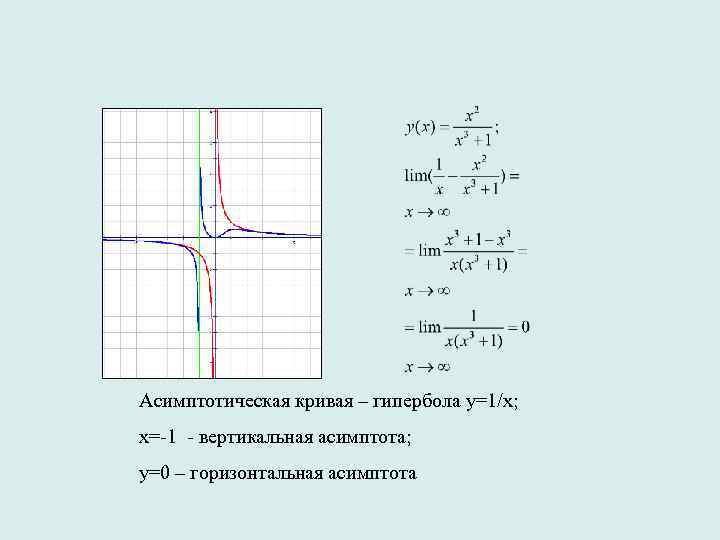
Асимптотическая кривая – гипербола у=1/x; х=-1 - вертикальная асимптота; у=0 – горизонтальная асимптота

Если показатель степени числителя на единицу меньше показателя степени знаменателя, то криволинейная асимптота представляет собой гиперболу у=1/х.
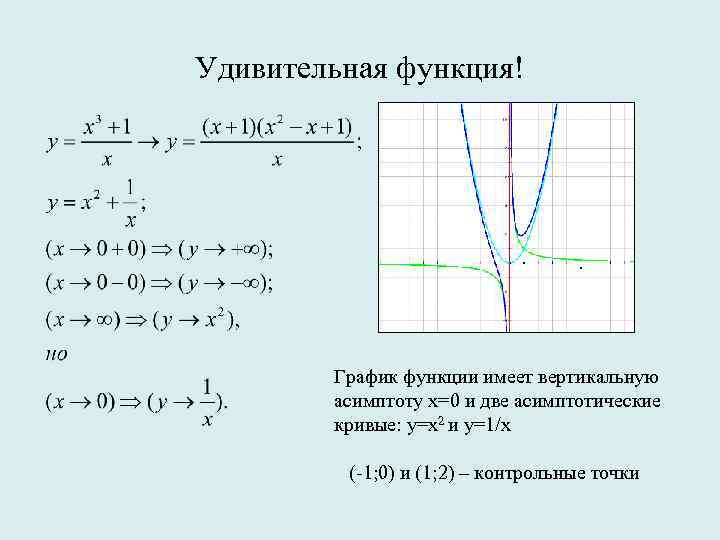
Удивительная функция! График функции имеет вертикальную асимптоту х=0 и две асимптотические кривые: у=х2 и у=1/х (-1; 0) и (1; 2) – контрольные точки
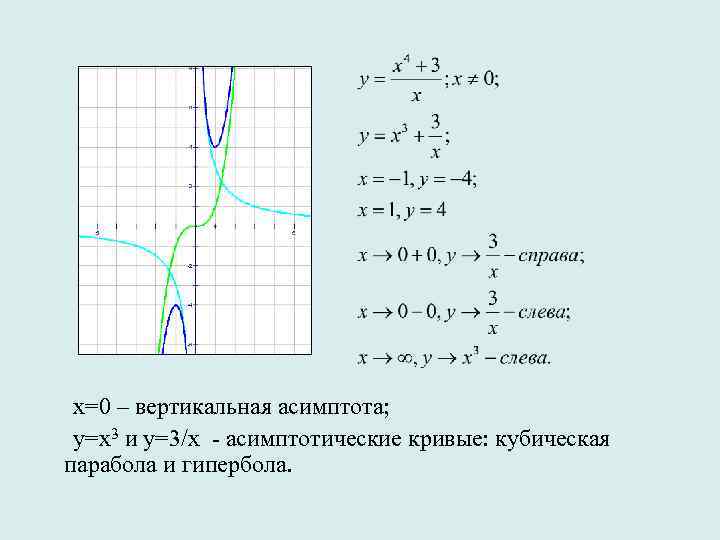
х=0 – вертикальная асимптота; у=х3 и у=3/х - асимптотические кривые: кубическая парабола и гипербола.
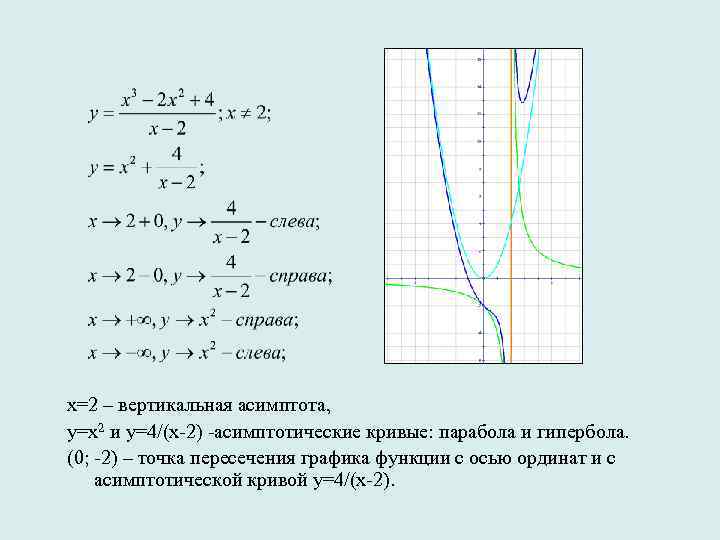
х=2 – вертикальная асимптота, у=х2 и у=4/(х-2) -асимптотические кривые: парабола и гипербола. (0; -2) – точка пересечения графика функции с осью ординат и с асимптотической кривой у=4/(х-2).
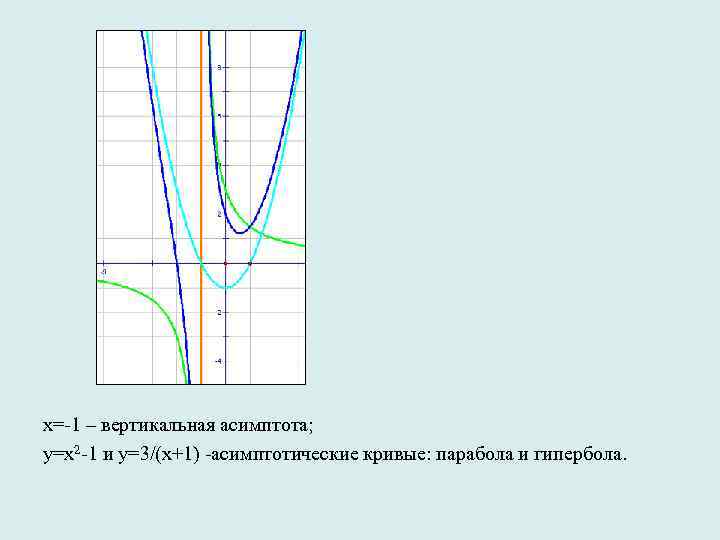
х=-1 – вертикальная асимптота; у=х2 -1 и у=3/(х+1) -асимптотические кривые: парабола и гипербола.
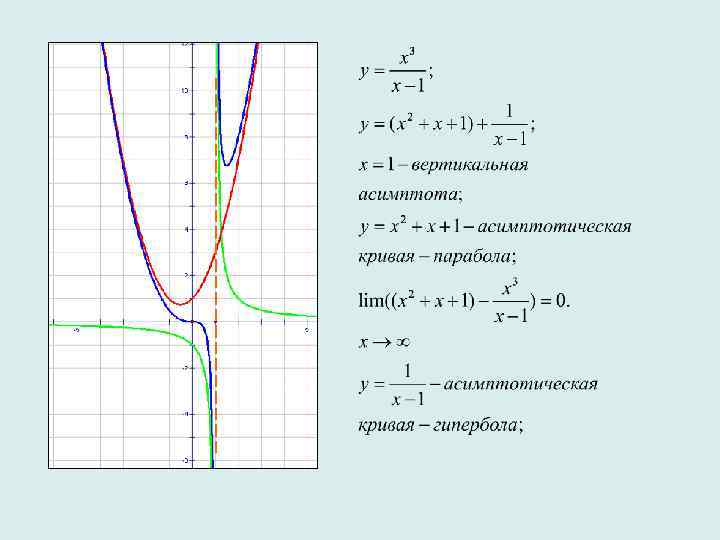

Как построить эскиз графика дробно-рациональной функции
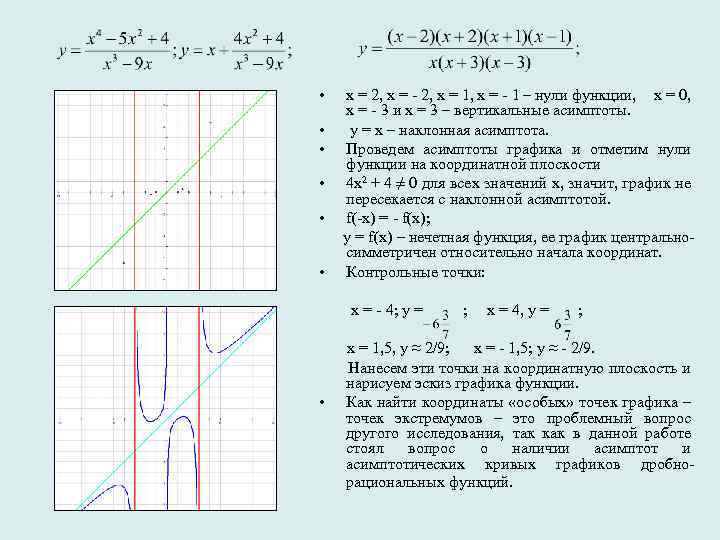
• х = 2, х = - 2, х = 1, х = - 1 – нули функции, х = 0, х = - 3 и х = 3 – вертикальные асимптоты. • у = х – наклонная асимптота. • Проведем асимптоты графика и отметим нули функции на координатной плоскости • 4 х2 + 4 ≠ 0 для всех значений х, значит, график не пересекается с наклонной асимптотой. • f(-x) = - f(x); y = f(x) – нечетная функция, ее график центральносимметричен относительно начала координат. • Контрольные точки: х = - 4; у = ; х = 4, у = ; х = 1, 5, у ≈ 2/9; х = - 1, 5; у ≈ - 2/9. Нанесем эти точки на координатную плоскость и нарисуем эскиз графика функции. • Как найти координаты «особых» точек графика – точек экстремумов – это проблемный вопрос другого исследования, так как в данной работе стоял вопрос о наличии асимптотических кривых графиков дробнорациональных функций.

На основании проведенных построений графиков дробно- • • рациональных функции можно сделать выводы: Если показатель степени числителя дробно-рационального выражения, задающего функцию на 1 больше показателя степени знаменателя этого выражения, то график функции может иметь не более одной вертикальной асимптоты и имеет наклонную асимптоту – прямую, которая задаётся уравнением у = ax+b, где а≠ 0. График может пересекать наклонную асимптоту. Если в дробно-рациональной функции показатель степени числителя на единицу меньше показателя степени знаменателя, то криволинейная асимптота представляет собой гиперболу у=1/х. График может иметь вертикальную и горизонтальную асимптоты. Если у=f(x)/g(x), где n-показатель степени числителя, k- показатель степени знаменателя, n-k равно числу 2, то криволинейная асимптота представляет собой параболу (т. е. у=x 2). Если n-k равно 3, то асимптотой служит график, сходный с графиком функции у=x 3, т. е. с кубической параболой. Если показатель степени числителя выражения, задающего функцию, на две единицы больше показателя степени знаменателя этого выражения, то график данной функции может иметь две асимптотические кривые – параболу и гиперболу.

В результате выполнения работы подтвердили гипотезу, что существуют дробно – рациональные функции, графики которых имеют не только вертикальную и горизонтальную или наклонную асимптоты, но и асимптотическую кривую. Ответили на основополагающий вопрос: может ли асимптотой графика дробно – рациональной функции быть парабола или гипербола? Привели примеры, когда график функции одновременно имеет две асимптотические кривые: параболу и гиперболу. Выявили возможность применения полученных результатов при построении графиков рассматриваемых функций. Ознакомились с технологией применения интерактивной среды «Живая геометрия» для построения графиков алгебраических функций. Приобретены конкретные знания и новый конкретный опыт по построению графиков дробно-рациональных функций.

http: //www. spr-formula. narod. ru/ При поиске материала в Интернете были найдены справочники, в которых приведено огромное количество готовых графиков дробнорациональных функций, но нет сведений как исследовать функцию и построить график.

Построение графиков функций элементарными методами (по страницам пособия для школьников, абитуриентов и учителей, автор Шахмейстер А. Х.

Пример 1. Исследуем функцию и построим эскиз ее графика (с. 133) у 1. 2. 3. D(y)=R, х≠ 2. Интервалы знакопостоянства, что дает возможность заштриховать области существования графика у=f(x). - -2 + 0 Асимптоты - 2 -2 0 + х Значит, х=2 – вертикальная асимптота 2 х
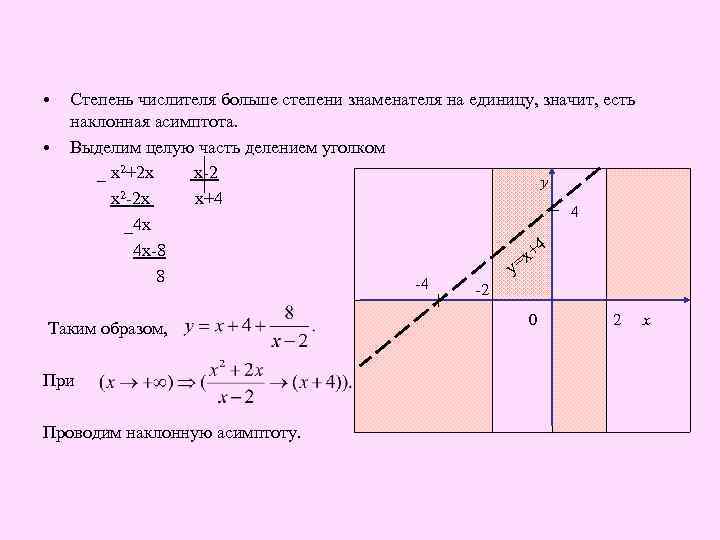
• Степень числителя больше степени знаменателя на единицу, значит, есть наклонная асимптота. • Выделим целую часть делением уголком _ х2+2 х х-2 у 2 -2 х х+4 х 4 _4 х 4 4 х-8 х+ у= 8 -4 -2 Таким образом, При Проводим наклонную асимптоту. 0 2 х

Так как график не пересекает наклонную асимптоту у=х+4. • При (х → ∞) график стремится немного выше асимптоты. • При (х → 2 + 0) график стремится k х = 2 справа (т. е. прих > 2 образует яму). • При (х → 2 - 0) график стремится к х = 2 слева, проходит через корни х = 0 и х = -2. • При (х → - ∞) стремится к у = х + 4 снизу (т. е. при х < 2 образует горку).

4) Найдем Е(у). ух - 2 у = х2 + 2 х; х2 + (2 - у)х + 2 у - 0; D = (2 - у)2 - 8 у = у2 - 12 у + 4 ≥ 0; у1, 2 = 6 ± √ 36 -4 = 6 ± 4√ 2. Следовательно, Е(у) = (-∞; 6 - 4√ 2] U [6 + 4√ 2; ∞).

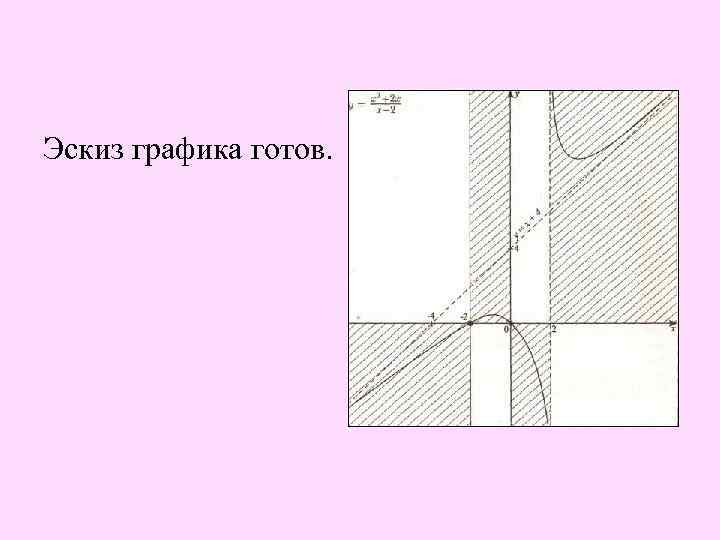
Эскиз графика готов. В сборнике представлено достаточно много графиков дробно-рациональных функций. Но только в одном примере показано как найти уmax и y min (с. 133 -134) и в нескольких примерах сделана ссылка «при желании можно уточнить координаты уmax и y min » (с. 163).
Эскиз графика готов.
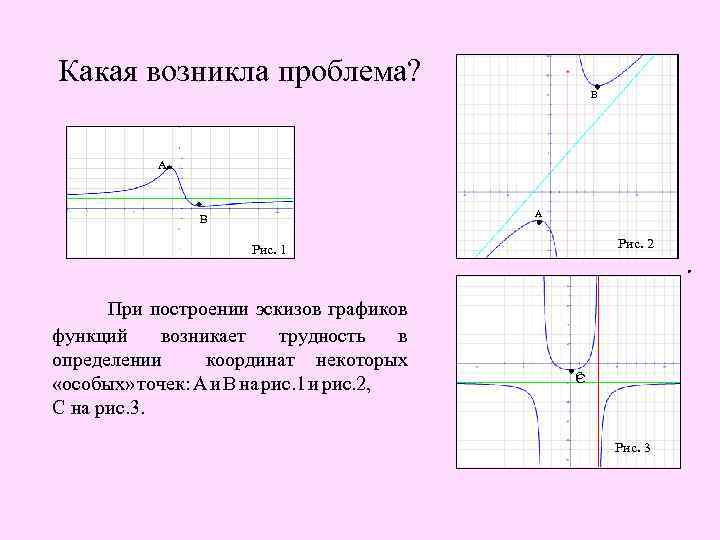
Какая возникла проблема? В А А В В Рис. 2 Рис. 1 При построении эскизов графиков функций возникает трудность в определении координат некоторых «особых» точек: А и В на рис. 1 и рис. 2, С на рис. 3. С С Рис. 3
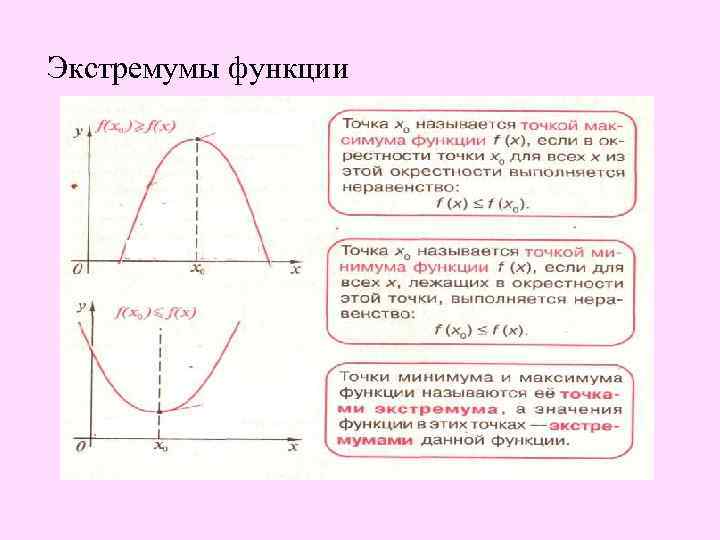
Экстремумы функции

Проблемный вопрос: Установить правило нахождения координат «особых» точек (в математике они называются экстремальными точками).

Объект исследования: графики дробно-рациональной функции, у которых степени числителя и знаменателя не ниже второй. Предмет исследования: координаты экстремальных точек графика дробно-рациональной функции Цель исследования: выяснить, как элементарными методами можно найти координаты экстремальных точек графика дробно-рациональной функции Гипотеза: для нахождения экстремумов дробнорациональной функции степени не выше второй нужно исследовать дискриминант данной дроби, выраженный через у.
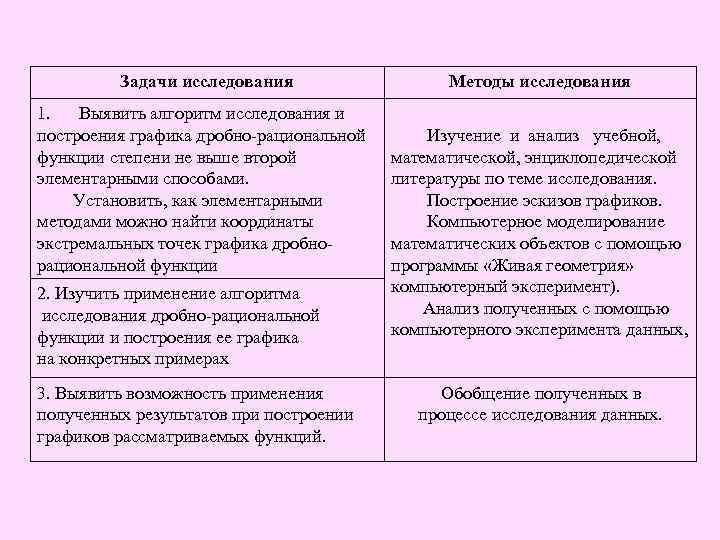
Задачи исследования Методы исследования 1. Выявить алгоритм исследования и построения графика дробно-рациональной функции степени не выше второй элементарными способами. Установить, как элементарными методами можно найти координаты экстремальных точек графика дробнорациональной функции Изучение и анализ учебной, математической, энциклопедической литературы по теме исследования. Построение эскизов графиков. Компьютерное моделирование математических объектов с помощью программы «Живая геометрия» компьютерный эксперимент). Анализ полученных с помощью компьютерного эксперимента данных, 2. Изучить применение алгоритма исследования дробно-рациональной функции и построения ее графика на конкретных примерах 3. Выявить возможность применения полученных результатов при построении графиков рассматриваемых функций. Обобщение полученных в процессе исследования данных.

• Горизонтальные асимптоты существуют у таких функций, у которых степень числителя не превышает степени знаменателя. • Вертикальные асимптоты существуют у таких функций, которые не определены в каких- либо точках. • Наклонные асимптоты существуют у таких функций, у которых степень числителя на единицу превышает степень знаменателя • У графика функции не могут существовать одновременно все три вида асимптот. Примечание. Мы будем рассматривать такие дробно-рациональные функции, у которых степень числителя и знаменателя дроби, стоящей в правой части, не превосходит двух.
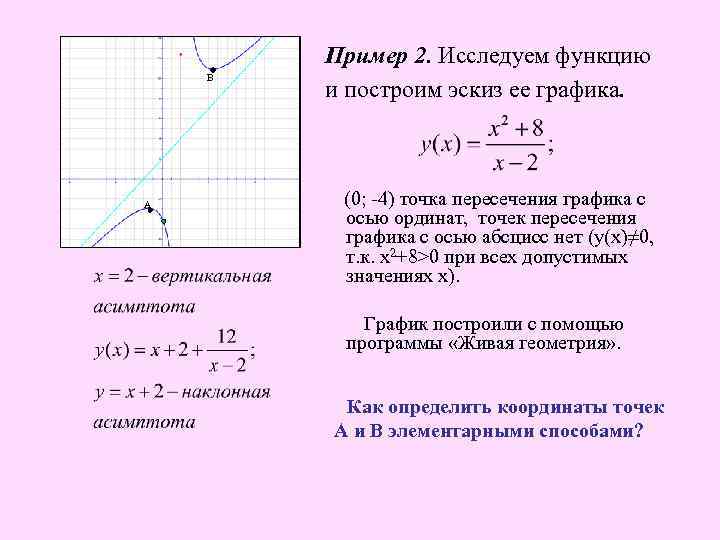
В А Пример 2. Исследуем функцию и построим эскиз ее графика. (0; -4) точка пересечения графика с осью ординат, точек пересечения графика с осью абсцисс нет (у(х)≠ 0, т. к. х2+8>0 при всех допустимых значениях х). График построили с помощью программы «Живая геометрия» . Как определить координаты точек А и В элементарными способами?

Основным методом при нахождении экстремумов дробно - рациональной функции степени не выше второй является исследование дискриминанта данной дроби, выражающегося через у. [Ажгалиев У. «Возможно ли исследование и построение графика дробно-рациональной функции без использования производной. » ( «Математика в школе» , № 7, 2010, ООО «Школьная Пресса» )].

Пример 2. Приведем данное выражение к следующему виду Это уравнение имеет решение тогда и только тогда , когда его дискриминант неотрицателен Решением неравенства является множество (-∞, 4 -4√ 3]U[4+4√ 3, + ∞)
![Решением неравенства является множество (-∞, 4 -4√ 3]U[4+4√ 3, + ∞). Это означает, Решением неравенства является множество (-∞, 4 -4√ 3]U[4+4√ 3, + ∞). Это означает,](https://present5.com/presentation/-32605811_151423760/image-139.jpg)
Решением неравенства является множество (-∞, 4 -4√ 3]U[4+4√ 3, + ∞). Это означает, что все значения функции принадлежат либо промежутку (-∞, 4 -4√ 3], либо промежутку [4+4√ 3, + ∞). Е(f)= (-∞, 4 -4√ 3]U[4+4√ 3, + ∞) Значения у=4 -4√ 3 и у=4+4√ 3 являются значениями минимума и максимума функции.

у=4 -4√ 3 и у=4+4√ 3 - ординаты точек А и В. Найдем абсциссы точек А и В. х2+8=(4 -4√ 3)х-8+8√ 3 , х2+8 -(4 -4√ 3)х+8 -8√ 3=0 , х2 -2(2 -2√ 3)х+(16 -8√ 3)=0, х2 -2(2 -2√ 3)х+(4 -8√ 3+12)=0, х2 -2(2 -2√ 3)х+(2 -2√ 3)2=0, (х-(2 -2√ 3))2=0, х-(2 -2√ 3)=0, х=2 -2√ 3. Значит, А(2 -2√ 3; 4 -4√ 3). х2+8=(4+4√ 3)х-8 -8√ 3 , х2+8 -(4+4√ 3)х+8+8√ 3=0 , х2 -2(2+2√ 3)х+(16+8√ 3)=0, х2 -2(2+2√ 3)х+(4+8√ 3+12)=0, х2 -2(2+2√ 3)х+(2+2√ 3)2=0, (х-(2+2√ 3))2=0, х-(2+2√ 3)=0, х=2+2√ 3. Значит, В(2+2√ 3; 4+4√ 3).

Нашли • уравнения вертикальной (х=2) и наклонной (у=х+2) асимптот графика данной функции, • вычислили координаты точек А(≈-1, 5; ≈ -2, 9) и В(≈5, 5; ≈ 10, 9), • установили, что график не пересекает ось абсцисс, ось ординат пересекает в точке С(0; -4), • Дополнительные точки: D(-4; -4), F(4; 12), Е(-4; -4), F(8. 12). • Можно нарисовать эскиз графика.
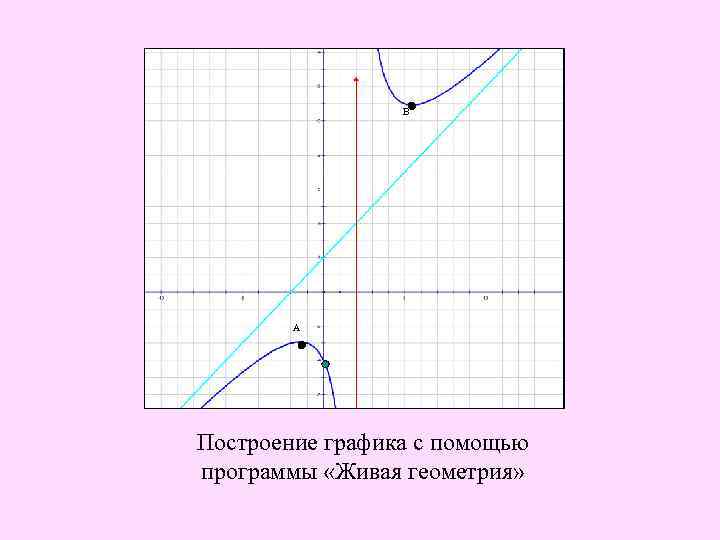
В А Построение графика с помощью программы «Живая геометрия»

Пример 3. Исследуем функцию и построим эскиз ее графика. • Трехчлен х2 -3 х+2 имеет корни 1 и 2; D(y)= (-∞; 1)U(1; 2)U(2; + ∞). Прямые х=1 и х=2 –вертикальные асимптоты. • Трехчлен 2 х2+3 х-2 имеет корни -2 и ½. График пересекает ось абсцисс в точках (-2; 0) и (½; 0).

Приведем данное выражение к виду: у(х2 -3 х+2)=2 х2+3 х-2, (у-2)х2 -(3 у+3)х+(2 у+2)=0, а=у-2, в =-(3 у+3), с=2 у+2; Это уравнение имеет решение тогда и только тогда , когда его дискриминант D=у2+26 у+25 неотрицателен. у2+26 у+25≥ 0. Решением неравенства является множество (-∞; -25]U[-1; +∞). Значения у=-25 и у =-1 являются значениями минимума или максимума функции. у≥-1, точка с координатами (0; -1) – точка минимума; у≤-25, точка с координатами (0; -25) – точка максимума.

По приведенному критерию легко видеть наличие горизонтальной асимптоты. При неограниченном увеличении |x| значение функции приближается к 2. График неограниченно приближается к прямой у=2 – горизонтальной асимптоте. Наклонной асимптоты график функции не имеет. Нарисуем эскиз графика.
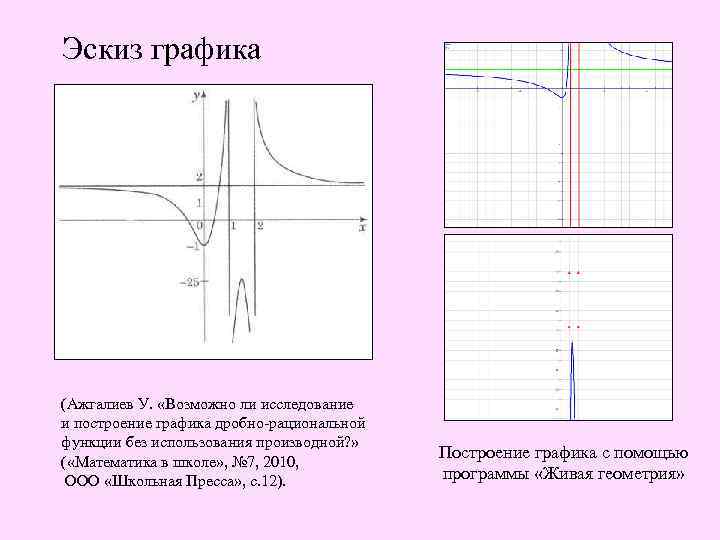
Эскиз графика (Ажгалиев У. «Возможно ли исследование и построение графика дробно-рациональной функции без использования производной? » ( «Математика в школе» , № 7, 2010, ООО «Школьная Пресса» , с. 12). Построение графика с помощью программы «Живая геометрия»

Пример 4. Исследуем функцию и построим эскиз ее графика. • Двучлен х2 -1 имеет корни -1 и 1; D(y)= (-∞; -1)U(-1; 1)U(1; + ∞). Прямые х=-1 и х=1 –вертикальные асимптоты. • Двучлен 5 х2+3 не имеет корней. График не пересекает ось абсцисс; ось ординат пересекает в точке (0; -3).

Приведем данное выражение к виду: у(х2 -1)=5 х2+3, (у-5)х2 -(у+3)=0, Это уравнение имеет решение тогда и только тогда , когда Решением неравенства является множество (-∞; -3]U(5; +∞). Значения у=-3 и у =5 являются значениями минимума или максимума функции. у>5, минимума нет; у≤-3, точка с координатами (0; -3) – точка максимума, точка пересечения графика с осью ординат.

По приведенному критерию легко видеть наличие горизонтальной асимптоты. При неограниченном увеличении |x| значение функции приближается к 5. График неограниченно приближается к прямой у=5 – горизонтальной асимптоте. Наклонной асимптоты график функции не имеет. Нарисуем эскиз графика.

Эскиз графика • х=-1 и х=1 –вертикальные асимптоты; • у=5 – горизонтальная асимптота; • график не пересекает ось абсцисс; • А(0; -3) – точка максимума, точка пересечения графика с осью ординат; • дополнительные точки: В(-3; 6); С(3; 6); D(2, 7⅔); Е(½; -5 ⅔); F(- ½; -5 ⅔).
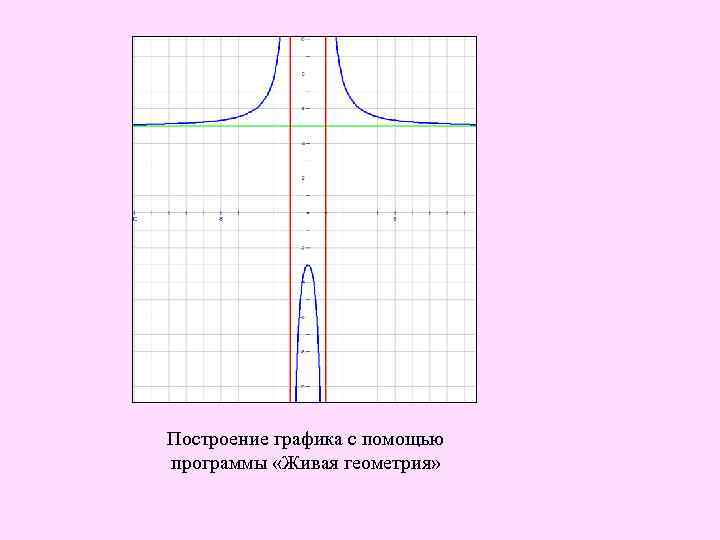
Построение графика с помощью программы «Живая геометрия»

Пример 5. Исследуем функцию и построим эскиз ее графика. • Трехчлен х2+х-12 имеет корни -4 и 3; D(y)= (-∞; -4)U(-4; 3)U(3; + ∞). Прямые х=-4 и х=3 –вертикальные асимптоты. • Трехчлен х2+5 х+24 не имеет корней. График не пересекает ось абсцисс. • х=0, у=-2; (0; -2) – точка пересечения графика с осью ординат

Приведем данное выражение к виду: у(х2+х-12)=х2+5 х+24, (у-1)х2+(у-5)х-(12 у+24)=0, а=у-1, в =у-5, с=-(12 у+24); Это уравнение имеет решение тогда и только тогда , когда его дискриминант D=49 у2+38 у-71 неотрицателен. 49 у2+38 у-71≥ 0. Решением неравенства является множество (-∞; ≈-1, 6]U[≈0, 9; +∞). Значения у ≈-1, 6 и у ≈0, 9 являются значениями минимума или максимума функции. у≥ ≈0, 9, точка с координатами (≈ -20; ≈0, 9) – точка минимума; у≤≈-1, 6, точка с координатами (≈-1, 5; ≈-1, 6) – точка максимума.

По приведенному критерию легко видеть наличие горизонтальной асимптоты. При неограниченном увеличении |x| значение функции приближается к 1. График неограниченно приближается к прямой у=1 – горизонтальной асимптоте и не пересекает ее. Наклонной асимптоты график функции не имеет. Нарисуем эскиз графика.
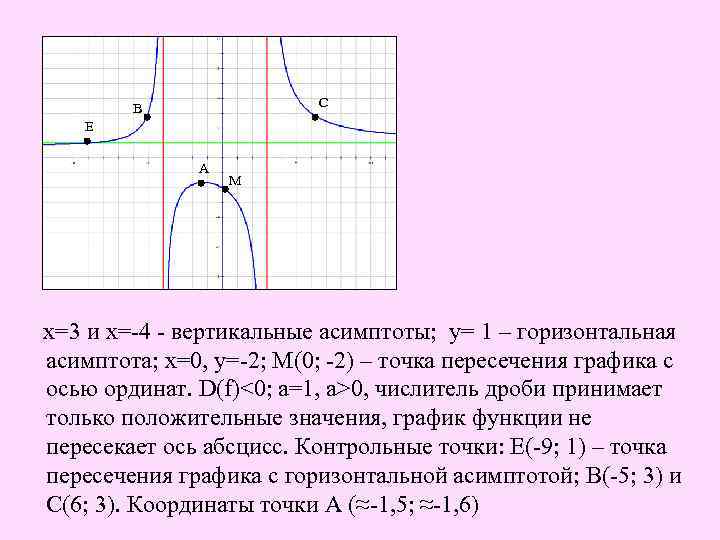
С В Е А М А х=3 и х=-4 - вертикальные асимптоты; у= 1 – горизонтальная асимптота; х=0, у=-2; М(0; -2) – точка пересечения графика с осью ординат. D(f)<0; а=1, a>0, числитель дроби принимает только положительные значения, график функции не пересекает ось абсцисс. Контрольные точки: Е(-9; 1) – точка пересечения графика с горизонтальной асимптотой; В(-5; 3) и С(6; 3). Координаты точки А (≈-1, 5; ≈-1, 6)

Пример 6. Исследуем функцию и построим эскиз ее графика. • Функция не определена прих=3. Прямая х=3 – вертикальная асимптота. • Трехчлен х2 -2 х+1 имеет корень х=1. График пересекает ось абсцисс в точке А(1; 0). • х=0, у=-2; В(0; -2) – точка пересечения графика с осью ординат.

Приведем данное выражение к виду: у(х-3)=х2 -2 х+1, х2 -(у+2)х+(3 у+1)=0, а=1, в =-(у+2)у-5, с=3 у+1; Это уравнение имеет решение тогда и только тогда , когда его дискриминант D=у2 -8 у неотрицателен. у2 -8 у≥ 0. Решением неравенства является множество (-∞; 0]U[8; +∞). Значения у =0 и у =8 являются значениями минимума или максимума функции.

у=0 и у=8 - ординаты точек А и В. Найдем абсциссы точек А и В. х2 -2 х+1=0, (х-1)2=0, х-1=0, х=1. Значит, А(1; 0). х2 -2 х+1=8 х-24, х2 -10 х+25=0, (х-5)2=0, х-5=0, х=5. Значит, В(5; 8). у≥ 8, точка с координатами С(5; 8) – точка минимума; у≤ 0, точка с координатами D(1; 0) – точка максимума.

По приведенному критерию легко видеть наличие наклонной асимптоты ( степень числителя данного выражения на единицу больше степени знаменателя). При неограниченном увеличении |x| значение выражения 4/(х-3) стремится к 0. График неограниченно приближается к прямой у=х+1 – наклонной асимптоте. Горизонтальной асимптоты график функции не имеет. Нарисуем эскиз графика.
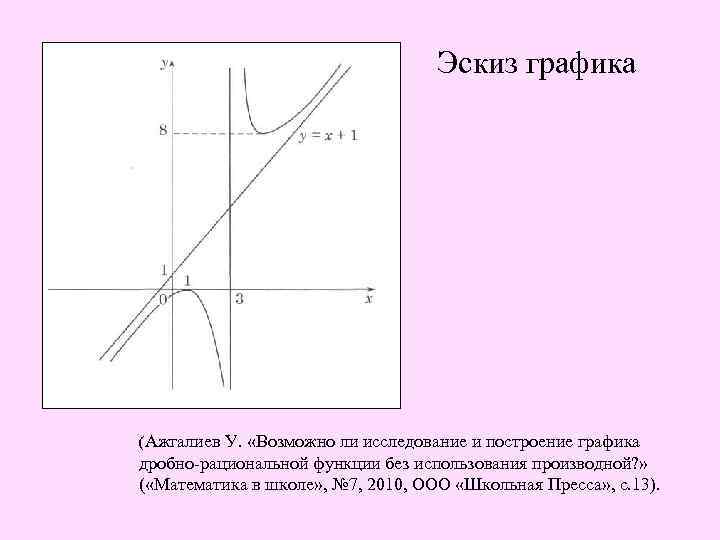
Эскиз графика (Ажгалиев У. «Возможно ли исследование и построение графика дробно-рациональной функции без использования производной? » ( «Математика в школе» , № 7, 2010, ООО «Школьная Пресса» , с. 13).
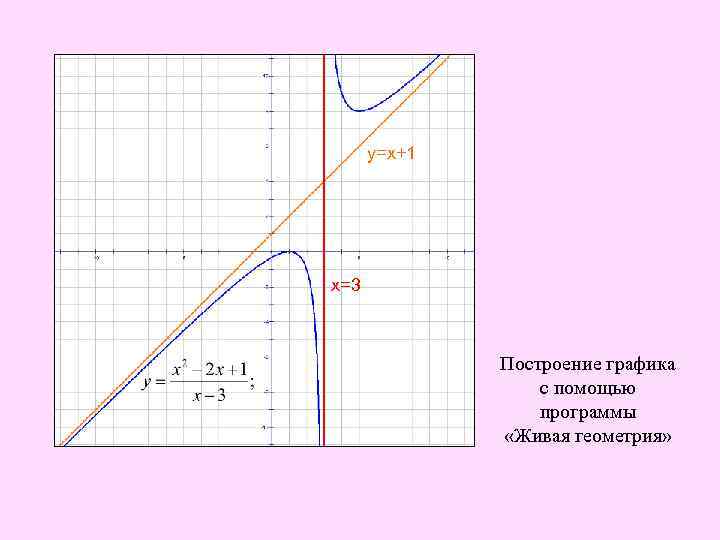
у=х+1 х=3 Построение графика с помощью программы «Живая геометрия»

Пример 7. Исследуем функцию и построим эскиз ее графика. • Функция не определена при х=2. Прямая х=2 – вертикальная асимптота. • Трехчлен х2 -х+2 не имеет корней. График не пересекает ось абсцисс. • х=0, у=-1; А(0; -1) – точка пересечения графика с осью ординат.

Приведем данное выражение к виду: у(х-2)=х2 -х+2, х2 -(у+1)х+(2 у+2)=0, а=1, в =-(у+1)у-5, с=2 у+2; Это уравнение имеет решение тогда и только тогда , когда его дискриминант D=у2 -6 у-7 неотрицателен. у2 -6 у-7≥ 0. Решением неравенства является множество (-∞; -1]U[7; +∞). Значения у =-1 и у =7 являются значениями минимума или максимума функции.

у=-1 и у=7 - ординаты точек E и F. Найдем абсциссы точек E и F. х2 -х+2=-(х-2), х2 -х+2=-х+2, х2 -х+2+х-2=0, х=0. Значит, А(0; -1). х2 -х+2=7 х-14, х2 -8 х+16=0, (х-4)2=0, х-4=0, х=4. Значит, В(4; 7). у≥ 7, точка с координатами В(4; 7) – точка минимума; у≤-1, точка с координатами А(0; -1) – точка максимума.

По приведенному критерию легко видеть наличие наклонной асимптоты ( степень числителя данного выражения на единицу больше степени знаменателя). При неограниченном увеличении |x| значение выражения 4/(х-3) стремится к 0. График неограниченно приближается к прямой у=х+1 – наклонной асимптоте. Горизонтальной асимптоты график функции не имеет. Нарисуем эскиз графика.
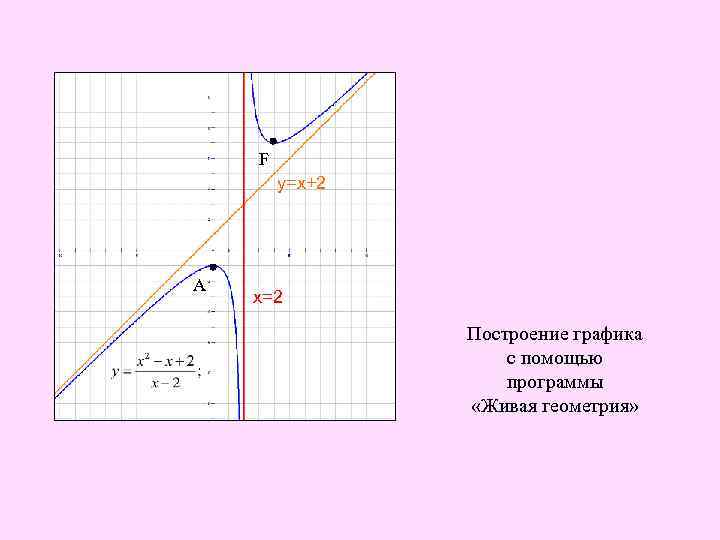
F у=х+2 А х=2 Построение графика с помощью программы «Живая геометрия»

Пример 8. Исследуем функцию и построим эскиз ее графика. • Функция не определена при х=-3 и х=1. Прямые х=-3 и х=1– вертикальные асимптоты. • Трехчлен х2 -х-2 имеет корни х=-1 и х=2. График пересекает ось абсцисс в точках А(-1; 0) и В(2; 0). • х=0, у=2/3; С(0; 2/3) – точка пересечения графика с осью ординат.

Приведем данное выражение к виду: у(х2+2 х-3)=х2 -х-2, ух2+2 ух-3 у-х2+х+2=0, (у-1)х2+(2 у+1)х+(2 -3 у)=0 а=у-1, в =2 у+1, с=2 -3; Это уравнение имеет решение тогда и только тогда , когда его дискриминант D=16 у2 -16 у+9 неотрицателен. 16 у2 -16 у+9≥ 0. Данное неравенство верно при всех значениях у. Функция не имеет экстремумов.

По приведенному критерию легко видеть наличие горизонтальной асимптоты При неограниченном увеличении |x| значение выражения у стремится к 1. График неограниченно приближается к прямой у=1 – горизонтальной асимптоте. Наклонной асимптоты график функции не имеет. Нарисуем эскиз графика.

Делаем эскиз графика х=-3 и х=1– вертикальные асимптоты. у=1 – горизонтальной асимптоте. Наклонной асимптоты нет. А(-1; 0), В(2; 0) и С(0; 2/3) – точки пересечения графика с осями координат Дополнительные точки D (-4; 3, 6), Е(-2; -4/3), F(-8; 14/9). Нарисуем эскиз графика.
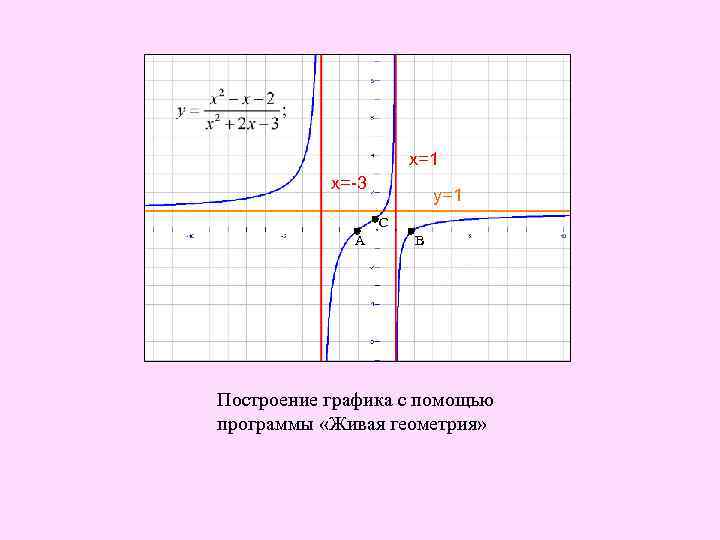
х=1 х=-3 у=1 С А В Построение графика с помощью программы «Живая геометрия»

Пример 9. Исследуем функцию и построим эскиз ее графика. • Функция не определена при х=2. Прямая х=2 – вертикальная асимптота. • Трехчлен 4 х2 -4 х+1 имеет корень х=0, 5. График пересекает ось абсцисс в точке А(0, 5; 0). • х=0, у=-0, 5; В(0; -0, 5) – точка пересечения графика с осью ординат.

Приведем данное выражение к виду: у(х-2)=4 х2 -4 х+1, ух-2 у-4 х2+4 х-1=0, -4 х2+(у+4)х-(2 у+1)=0 а=-4, в =у+4, с=-(2 у+1); Это уравнение имеет решение тогда и только тогда , когда его дискриминант D=у2 -24 у неотрицателен. у2 -24 у≥ 0. Решением неравенства является множество (-∞; 0]U[24; +∞). Значения у =0 и у =24 являются значениями минимума или максимума функции. .

у=0 и у=24 - ординаты точек А и С. Найдем абсциссы точек А и С. 4 х2 -4 х+1=0, (2 х-1)2=0, 2 х-1=0, х=0, 5. Значит, А(0, 5; 0). 4 х2 -4 х+1=24 х-48, х2 -28 х+49=0, (х-7)2=0, х-7=0, х=7. Значит, С(7; 24). у≥ 24, точка с координатами С(7; 24) – точка минимума; у≤ 0, точка с координатами А(0, 5; 0) – точка максимума.
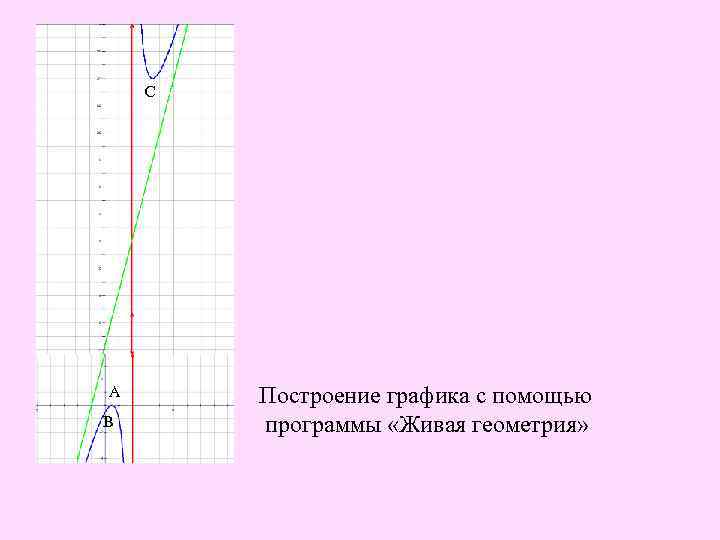
С А А В В Построение графика с помощью программы «Живая геометрия»

Выводы • В результате выполнения работы подтвердили гипотезу: действительно график дробно-рациональной функции степени не выше второй можно построить методами элементарной математики. • Был выработан алгоритм исследования и построения графика дробно-рациональной функции степени не выше второй элементарными способами: 1. установим наличие асимптот; 2. найдем точки пересечения графика с осью абсцисс, приравняв числитель к нулю; вычислим координаты точек пересечения графика с осью ординат (найдем значение функции при х=0) 3. найдем область значений данной функции; 4. найденные значения у1 и у2 являются значениями минимума или максимума функции. Приравняв дробь к этим числам, вычислим абсциссы указанных точек. 5. учитывая множество значений функции, определяем, какая из точек является точкой минимума, а какая – точкой максимума.

Источники информации 1. Ажгалиев У. «Возможно ли исследование и построение графика дробно-рациональной функции без использования производной? » ( «Математика в школе» , № 7, 2010, ООО «Школьная Пресса» ; 2. лгебра. 9 класс: учебник для общеобразовательных учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - М. : Просвещение, 2009. – 271 с. ; 3. Алгебра. 8 класс: учеб. Для учащихся общеобразовательных учреждений/Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов-М: Мнемозина, 2009. – 384 с. ). 4. Большая советская энциклопедия http: //dic. academic. ru. 5. Большой энциклопедический словарь Брокгауза Ф. А. , Ефрона И. А. , http: //dic. academic. ru 6. Википедия ru. wikipedia. org/wiki/Асимптота 7. Вирченко Н. О. , Ляшко И. И. , Швецов К. И. Графики функций. Справочник. /Киев, Наукова думка, 1977. -320 с. ; 8. Гельфанд И. М. , Глаголева Е. Г. , Шноль Э. Э. Функции и графики (основные приемы) /М. : МЦНМ, 2004. -120 с. ; 9. Глейзер Г. И. История математики в средней школе /М. : Просвещение, 1970. -461 с. 10. Гурский И. П. Функции и построение графиков/ М. : Просвещение, 1968. -215 с. ; 177

Источники информации 11. Егерев В. К. , Радунский Б. А. , Тальский Д. А. Методика построения графиков функций. Учебное пособие для студентов вузов /М. : Высшая школа, 1970, - 152 с. 12. Ершов Л. В. , . Райхмист Р. Б Построение графиков функций: книга для учителя. - М. : Просвещение, 1984. -80 с. ; 13. Курс математики для техникумов под редакцией Матвеева Н. М. / Москва, «Наука» 1977 -368 с. ; 14. Литинский Г. И. Функции и графики , -М. : Аслан, 1995. -192 с. ; 15. Мышкис А. Д. , Сатьянов П. Г. Функции и графики, с. 248 /Факультативный курс по математике: Учебное пособие для 7 -8 кл. сред. шк. / сост. И. Л Никольская, - М. : Просвещение, 1991. -383 с. ; 16. Шахмейстер Построение графиков элементарными методами/ СПб; Че. Ро-на –Неве, 2003. -184 с. ; 17. Шилов Г. Е. Как построить график/ М. : Государственное издательство физико-математической литературы, 1954. -24 с. ; 18. Энциклопедический словарь юного математика /Сост. А. П. Савин. - М. : Педагогика, 1989. -352 с. . 178

Aσϋμπτωτος Asymptote асимптота
47507.ppt