Zaawansowane Protokoły Kryptograficzne część I 1 Dowody z

Zaawansowane Protokoły Kryptograficzne część I 1. Dowody z wiedzą zerową 2. Obliczenia wielopodmiotowe 3. Elektroniczne wybory 4. Cyfrowa gotówka

Dowody z wiedzą zerową Alicja: „Znam hasło do systemu NBP, składniki tajnego sosu Mc. Donald’s i treść czwartego tomu biblii Knuth’a. ” Bob: „Niemożliwe. ” Alicja: „Właśnie, że znam. ” Bob: „Udowodnij. ” Alicja: Szepce Bobowi swoje tajemnice na ucho. Bob: „Ha ha ha. Gazety na pewno będą zainteresowane. ”

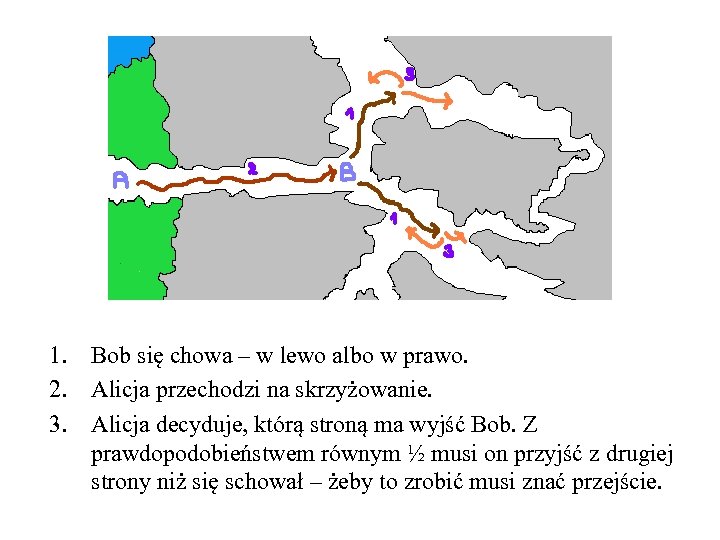1. Bob się chowa – w lewo albo w prawo. 2. Alicja przechodzi na skrzyżowanie. 3. Alicja decyduje, którą stroną ma wyjść Bob. Z prawdopodobieństwem równym ½ musi on przyjść z drugiej strony niż się schował – żeby to zrobić musi znać przejście.

Bob (P) chce udowodnić Alicji (V), że x L, ale tak żeby nie ujawnić nic poza samym tym faktem (w szczególności nie ujawnić x). Interaktywna Maszyna Turinga (IMT) – ma w sumie sześć taśm: wyjście tylko do pisania, wejście tylko do czytania, taśmę z losowymi bitami, taśmę do obliczeń, zwykłe wejście i zwykłe wyjście. Akceptuje przez przejście do odpowiedniego stanu. Protokół interaktywny – para sprzężonych IMT’ów (P, V) ze wspólnym wejściem, pracujących i wysyłających wiadomości na zmianę. P nieograniczona obliczeniowo, V ograniczona wielomianowo. Język L ma dowód interaktywny jeśli: Istnieje taka IMT V, że: i. IMT P, (P, V) jest dowodem interaktywnym x L, |x| dostatecznie duże P[V akceptuje] > 2/3 ii. IMT P, (P, V) jest dowodem interaktywnym x L, |x| dostatecznie duże P[V akceptuje] < 1/3

Nieizomorfizm grafów Przykład języka z dowodem interaktywnym. Dane są dwa grafy – G 1 i G 2. Chcemy udowodnić, że nie są izomorficzne. • V wybiera losowo jeden z grafów, tworzy losowy graf z nim izomorficzny (permutuje wierzchołki) i wysyła P. • P odpowiada, który graf V wybrał.

Niereszty kwadratowe QNR = {(x, n) : x < n, x n i y y 2 x mod n} Dowodzimy, że (x, n) należy do QNR. k = |n|, i = 1. . k • V wybiera losowo zi Zn*, bi {0, 1}. Wysyła wi = xbizi 2 (mod n). • P odsyła ci = [wi jest resztą kwadratową modulo n]. • V akceptuje jeśli i bi = ci. Na przykład: x = 5, n = 6 (Z 6* = {1, 5}, QR 6 = {1}, QNR 6 = {5}, k = 3) V losuje: z 1 = 1, z 2 = 5, z 3 = 5; b 1 = 1, b 2 = 0, b 3 = 1. V wysyła: 1, 5, 1. P ma nieograniczoną moc, stwierdza więc, że 1 jest resztą, a 5 nieresztą kwadratową mod 6. P odsyła: 1, 0, 1

Cykle Hamiltona Język: grafy mające cykl Hamiltona. • P losowo permutuje wierzchołki grafu; zobowiązuje się bitowo do każdej krawędzi w nowym grafie. • V wybiera, czy zapytać o permutację, czy o cykl. • P otwiera wszystkie zobowiązania i pokazuje permutację albo otwiera tylko zobowiązania krawędzi na cyklu. Jeśli weryfikator wybiera opcje losowo, to gdy dowodzący nie zna cyklu Hamiltona w grafie, może go oszukać z prawdopodobieństwem równym ½. Weryfikator widzi tylko albo losową permutację grafu albo ścieżkę w grafie, którego nie zna.

Wiedza zerowa Dowód interaktywny jest z wiedzą zerową jeśli wszystko co może wyliczyć weryfikator po udziale w protokole, mogłoby zostać policzone w czasie wielomianowym przez probabilistyczną maszynę Turinga bez interakcji z dowodzącym. Dokładniej. Niech (P, V) będzie dowodem interaktywnym dla języka L. Jest on dowodem z wiedzą zerową (doskonałą / statystyczną / obliczeniową) jeśli dla dowolnego WAP’a V*, istnieje WAP’a M*, taki że ciągi zmiennych losowych: • {(P, V*)(x))}x L • {(M*(x))}x L są odpowiednio nierozróżnialne. X = {X } S, Y = {Y } S d(n) = max : | | = n {|P[A(X , ) = 1] – P[A(Y , ) = 1]|} X i Y są nierozróżnialne obliczeniowo jeśli WAP A d(n) jest zaniedbywalne. Bez ograniczenia mocy obliczeniowej A mamy statystyczną nierozróżnialność, a jeśli dodatkowo d(n) 0 to jest ona doskonała.

Protokół Fiata-Shamira Wykorzystujemy dowód z wiedzą zerową jako schemat identyfikacji. Użytkownik dowodzi systemowi, że zna pierwiastek pewnej liczby modulo liczba złożona. Klucz prywatny: (s, n), klucz publiczny: (r, n), takie że r = s 2 (mod n). Użytkownik losuje zi {0, . . . , n-1}. Wysyła wi = zi 2 (mod n). System odsyła losowe bi {0, 1}. Użytkownik odpowiada wysyłając ui = zisbi (mod n). System akceptuje jeśli ui 2 = wirbi (mod n).

NP KC[0] Twierdzenie: Jeśli istnieje (niejednolicie) wielomianowo-bezpieczny schemat szyfrowania, to każdy język w NP ma interaktywny system dowodowy z wiedzą zerową (obliczeniową). Dowód: System dla NP-zupełnego języka – grafów trójkolorowalnych. Chcemy przekonać weryfikatora, że graf można pokolorować trzema kolorami – bez ujawniania nic o kolorowaniu. Możemy to zrobić w |E|2 krokach: • Losowo zamieniamy kolory (np. : żółty na czerwony, czerwony na niebieski, niebieski na żółty). • Szyfrujemy kolor każdego wierzchołka przy użyciu innego klucza – i wysyłamy weryfikatorowi (razem z nazwami wierzchołków: ). • On odpowiada nam losową krawędzią grafu. • Wysyłamy klucze do kolorów wierzchołków na końcach tej krawędzi (kolory mają być różne).

Ataki ze środka Partia z arcymistrzem Jak każdy może wygrać partię z arcymistrzem szachowym ? Wystarczy, że umówi się jednocześnie na partię, na przykład, z Karpowem i Kasparowem (najlepiej korespondencyjne) i będzie powtarzał ruchy jednego w partii drugiego, a drugiego w partii pierwszego. Identyfikacja Przyjaciel-Wróg

Obliczenia wielopodmiotowe

Grupa stron chce skoordynować działania, żeby osiągnąć jakiś cel – nawet jeśli część z nich jest nieuczciwa. Dokładniej: Rozważamy grupę graczy P 1, . . . , Pn. Każdy z nich ma prywatne wejście – xi. Niech y = f(x 1, . . . , xn). Chcemy skonstruować taki protokół, żeby każdy poznał y – ale żaden nie ujawnił swojego wejścia. Mamy przeciwnika. Może on „korumpować” graczy. I to na dwa sposoby: • pasywnie – dostaje wszystkie informacje, którymi dana strona dysponuje (włącznie z jej wejściem), • aktywnie – nad tymi graczami ma pełną kontrolę, decyduje o ich wyborach i komunikacji. Aby zdefiniować bezpieczeństwo wyobraźmy sobie, że mamy dodatkowego, niekorumpowalnego gracza. Postępujemy następująco: Wszyscy wysyłają swoje wejścia do tego uczciwego, on oblicza wartość funkcji i rozsyła ją do wszystkich. Protokół jest bezpieczny jeśli wszystko co może w nim osiągnąć przeciwnik może osiągnąć również w powyższym (idealnym) modelu. (Może on, na przykład, wpłynąć na wynik podmieniając wejście aktywnie skorumpowanego gracza. )

Przykłady Problem z miłością Alicji i Boba: • chcą sprawdzić, czy się kochają nawzajem • trzymają swoje uczucia w największym sekrecie To znaczy: Alicja ma prywatne wejście a = [Alicja kocha Boba], a Bob ma prywatne wejście b = [Bob kocha Alicję]. Chcą obliczyć funkcję: f(a, b) = a b. Problem majątków miliarderów: Grupa bogaczy chce się dowiedzieć, który ma największą (najmniejszą) fortunę, ale żaden nie chce się przyznać ile ma. Strony: B 1, . . . , Bn. Wejścia: f 1, . . . , fn. Funkcja: f(f 1, . . . , fn) = maxi fi

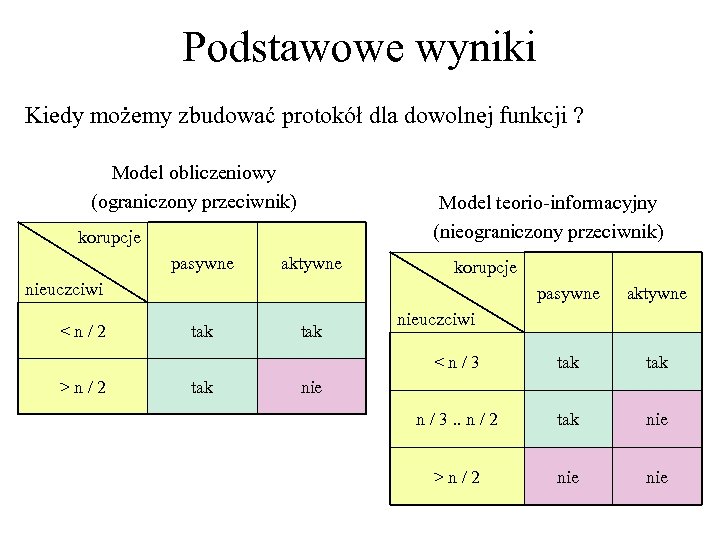Podstawowe wyniki Kiedy możemy zbudować protokół dla dowolnej funkcji ? Model obliczeniowy (ograniczony przeciwnik) Model teorio-informacyjny (nieograniczony przeciwnik) korupcje pasywne aktywne korupcje nieuczciwi >n/2 tak tak aktywne n/2 nie nieuczciwi nie

Dzielenie Sekretu Podstawowy protokół – i narzędzie. Przykład: Masz klucz do ważnego systemu, nie chcesz go zgubić, ale nie możesz zaufać żadnej jednej osobie. (Nie koniecznie dlatego, że nikt nie jest warty zaufania. Być może w okolicy kręcą się terroryści? : ) Protokół Shamira (s – sekret): Weźmy wielomian stopnia d: f(x) = s + a 1 x +. . . + adxd (ai losowe). Każdemu graczowi dajemy wartość wielomianu w jakimś punkcie, na przykład: si = f(i). Jeśli spotka się d + 1 graczy to mogą oni wyliczyć s przez interpolację (s = icisi, ci = const. ). Nawet mając d punktów na wielomianie możemy odtworzyć s (dla każdej jego wartości jest jeden wielomian przechodzący przez wszystkie te punkty).

Weryfikowalne Dzielenie Sekretu Pomysł Shamira ma dwie wady. Po pierwsze, jeśli dealer (dzielący sekret) jest nieuczciwy może rozdać takie udziały, które nie określą unikalnej wartości. Po drugie, jeśli jakiś gracz jest nieuczciwy, to może przy rekonstrukcji dostarczyć wartości, które spowodują, że zostanie odtworzony niewłaściwy sekret. Możemy to poprawić przy użyciu bezpiecznego kanału rozgłoszeniowego. (istnieje VSS symulacja kanału jest możliwa). Struktura sekretności : rodzina zbiorów graczy zamknięta ze względu na branie podzbiorów. Jeśli grupa graczy X to wymagamy, aby nie miała ona żadnej informacji na temat sekretu. Dla każdej grupy X chcemy, aby mogła ona obliczyć sekret. Niech T 1, . . . , Tn zbiory maksymalne struktury (żeby algorytm działał musi ona spełniać pewien warunek). Dealer dzieli s na s 1, . . . , sn; takie że: s = s 1 +. . . + sn. Rozsyła udziały do graczy. Dla każdego udziału si i każdej pary graczy (Pa, Pb), takiej że: Pa, Pb Ti’: Pa i Pb wysyłają do siebie to co otrzymali jako si (jeśli się nie zgadza to protestują przy użyciu kanału). Dealer ogłasza przez kanał wszystkie wartości si, co do których były protesty (jeśli tego nie zrobi wszyscy przyjmują si = 0). Po wykonaniu tego protokołu uczciwi gracze mają spójną wiedzę.

Oblivious Transfer oblivion [ә’bliviәn] – 1 a state in which one is no longer aware or conscious of what is happening 2 the state of being forgotten especially by the public Historycznie bardzo ważny protokół. Pojawia się w dwóch równoważnych wersjach: 1. Nadawca przesyła wiadomość odbiorcy. Prawdopodobieństwo, że ten ją otrzyma wynosi ½; nadawca nie ma żadnej informacji o tym, czy odbiorca otrzymał wiadomość. 2. Nadawca ma wektor wartości: a 1, . . . , an. Odbiorca ma i {1, . . . , n}. W wyniku protokołu odbiorca poznaje ai (i tylko ai); nadawca nie dowiaduje się nic o i. Nadawca generuje i wysyła n-bitową liczbę Blum’a N. (N = pq; p, q – pierwsze; p q 3 mod 4; |lg p/q| < 2) Nadawca przekonuje odbiorcę, że N jest liczbą Blum’a. (ewentualnie może być: N = p 2 m+1 q 2 n+1) Odbiorca wybiera losowe z ZN. Wysyła z 2 mod N. Nadawca wysyła: M 2 mod N, b = symbol Jacobiego (M|N) i w = losowy pierwiastek M 2 z 2 mod N (te rzeczy jednoznacznie definiują wiadomość). Odbiorca sprawdza czy w 2/z 2 M 2 mod N. Jeśli symbol Jacobiego (w/z|N) = b, to właśnie odebrał on wiadomość.

Elektroniczne Wybory 8 ways to steal an election: (. . . ) 1. Use machines & Internet to vote. This prohibits direct voter participation in and oversight of the entire voting process. It is also an open invitation to massive vote fraud and technical failure. (. . . ) 8. Just buy it. Allow wealth to concentrate in the hands of a few. www. ecotalk. org

Wymagania 1. 2. 3. 4. 5. 6. 7. 8. Tylko autoryzowani wyborcy mogą głosować. Nikt nie może głosować więcej niż raz. Zachowana jest prywatność głosujących. Nikt nie może powielić, powtórzyć czyjegoś głosu. Wynik jest policzony prawidłowo i każdy może to sprawdzić. Protokół powinien działać nawet w obecności koalicji nieuczciwych uczestników (również organizatorów). Obsługa protokołu (przynajmniej dla głosujących) powinna być prosta i efektywna. Głosujący nie może zostać zmuszony do ujawnienia głosu.

Homomorficzne zobowiązania Do konstrukcji protokołu potrzebujemy schematu zobowiązania, spełniającego warunek: B(x + y) = B(x) • B(y). Możemy to zrealizować na przykład w oparciu o problem logarytmu dyskretnego. Niech p będzie liczbą pierwszą postaci: p = kq + 1. Niech g i h będą elementami podgrupy Zp* rzędu q. Zakładamy, że nikt nie zna logarytmów przy bazie g i h. Wybieramy a losowo. Ba(m) = gahm jest zobowiązaniem do m {1, . . . , q} Żeby otworzyć zobowiązanie ujawniamy a.

Protokół Głosowania Merritt’a Jeden z najbardziej efektywnych protokołów. Spełnia wszystkie wymagania poza niemożliwością sprzedaży głosów (8). Do sprawdzenia wyników nie wymaga kooperacji wszystkich wyborców (5+). Do jego realizacji potrzebne jest: zobowiązanie takie jak na poprzednim slajdzie, asymetryczny schemat szyfrowania i tablice ogłoszeń. Głosy są równe – 1 albo 1. Wszystkie obliczenia odbywają się w Zp. Mamy n organizatorów: O 1, . . . , On. Niech Ei – funkcja szyfrująca Oi. Każdy głosujący Vj, chciałby oddać głos vj. Wybiera, więc losowe aj.

Głosowanie: Po pierwsze, głosujący zobowiązuje się do swojego głosu – publikuje Bj = Baj(vj). Wykonuje również dowód z wiedzą zerową, aby pokazać, że jego głos jest poprawny (za chwilę). Po drugie, dzieli aj i vj między organizatorów za pomocą schematu Shamira (z progiem t) – wybiera dwa wielomiany o losowych współczynnikach: Sj(x) = aj + s 1, jx +. . . + st, jxt i Rj(x) = vj + r 1, jx +. . . + rt, jxt. I wysyła do każdego Oi (zaszyfrowane Ei) wartości wielomianów w i: wi, j = Sj(i) i ui, j = Rj(i). Na koniec zobowiązuje się do współczynników wielomianów ogłaszając: Bl, j = Bsl, j(r 1, j) Organizator sprawdza, czy: gwi, jhui, j = Bj l=1. . t Bl, jil

Liczenie głosów: Każdy organizator ogłasza sumy częściowe – jego udziały w losowościach i głosach: Ai = j wi, j Ti = j ui, j Każdy może sprawdzić, że powyższe są prawidłowe: g. Aih. Ti = j(Bj l=1. . t Bl, jil) Wartości Ti są poprawnymi udziałami w podziale sumy głosów. Wystarczy znaleźć t + 1 takich poprawnych udziałów, aby móc interpolować wynik wyborów. Dowód poprawności głosu: (dla v = 1) Niech B = Ba(v) – zobowiązanie do głosu. Głosujący wybiera losowe r 1, d 1, w 2 i publikuje 1 = gr 1(B/h)-d 1 i 2 = gw 2. Na wyzwanie c odpowiada przez: r 1, d 2 = c – d 1, r 2 = w 2 + ad 2. (może być c = H( ) ? ? ? ) 1 Dowód jest poprawny jeśli: c = d 1 + d 2, gr 1 = 1(Bh)d 1 i gr 2 = 2(B/h)d 2. Dla v = – 1 jest symetrycznie (i nie da się poznać, który to przypadek).

Cyfrowe pieniądze

Wymagania bis Jakich właściwości oczekujemy od protokołu elektronicznej gotówki ? • fałszerstwo ma być trudne • powielanie powinno być albo niemożliwe, albo chociaż wykrywalne • schemat ma umożliwiać użytkownikowi zachowanie anonimowości (nie można go połączyć z jego transakcjami) • im mniej operacji on-line, tym lepiej Schemat cyfrowych pieniędzy zazwyczaj składa się z trzech protokołów: • wypłacanie – użytkownik pobiera pieniądze z banku • płacenie – użytkownik przekazuje pieniądze (może nawet dostaje coś w zamian) sprzedawcy • deponowanie, przez sprzedawcę pieniędzy otrzymanych od kupującego (powiększanie stanu swojego konta albo zamiana na tradycyjną gotówkę).

Prosty (kiepski) protokół Wypłacanie: Użytkownik informuje bank, że potrzebuje 100 zł. . Bank zwraca banknot, który wygląda następująco: {Jestem banknotem 100 złotowym, #0123}SKB (I zabiera 100 zł. z konta użytkownika. ) Użytkownik sprawdza podpis – jeśli jest prawidłowy przyjmuje banknot. Płacenie: Użytkownik przekazuje sprzedawcy banknot. Sprzedawca akceptuje jeśli podpis jest poprawny. Deponowanie: Sprzedawca przekazuje banknot bankowi. Bank akceptuje jeśli podpis jest jego i nie otrzymał jeszcze banknotu z danym numerem. Jedynym spełnionym wymaganiem jest brak możliwości podrobienia pieniędzy.

Skomplikowany protokół H – jednokierunkowa funkcja skrótu Wypłacanie: Użytkownik przygotowuje 10 banknotów: Bi = {Jestem banknotem 30 złotowym, #0123, yi, 1’, . . . , yi, K’}, gdzie: yi, j = H(xi, j), yi, j’ = H(xi, j’), a xi, j, xi, j’ są losowo wybrane, tak aby: xi, j’ = Nazwa Użytkownik zaciemnia wszystkie banknoty. Bank wybiera 9 banknotów, które użytkownik ma ujawnić (jeśli ich nie ujawni albo coś będzie nie w porządku to idzie za kratki!). Bank potwierdza, że banknoty są poprawne – zgadza się nominał i podpisy użytkownika. Bank podpisuje jedyną wciąż zaciemnioną wiadomość (od tej pory B). Płacenie: Użytkownik przekazuje sprzedawcy B z podpisem. Jeśli podpis jest poprawny, sprzedawca odpowiada losowym ciągiem bitów: b 1, . . . , b. K. Dla każdego j, jeśli bj = 0 użytkownik ujawnia xi, j, jeśli bj = 1 to xi, j’. Sprzedawca sprawdza, czy wartości H(x , ) zgadzają się z tymi na banknocie.

Deponowanie: Sprzedawca przekazuje banknot bankowi razem z ciągiem wylosowanych bitów i ciągiem ujawnionych przez kupującego wartości. Bank akceptuje jeśli podpis jest jego i nie otrzymał jeszcze banknotu z danym numerem. Jeśli pieniądz jest już w banku to bank porównuje dodatkowe ciągi: jeśli są takie same oszukuje sprzedawca, jeśli różne winny jest użytkownik. Ten schemat ma wszystkie potrzebne własności: • Pieniądze są podpisywane przez bank, więc ich sfałszowanie jest bardzo trudne. • Powielanie zarówno przez użytkownika, jak i sprzedawcę jest wykrywane. • Anonimowość jest zachowana. Bank podpisuje zaciemniony banknot, więc nie może po jego otrzymaniu skojarzyć go z użytkownikiem. Ale. Jeśli użytkownik próbuje oszukiwać, to bank otrzyma dwa różne ciągi połówek jego identyfikatora – czyli może go odtworzyć. • Dużą zaletą jest brak potrzeby komunikacji z bankiem w momencie sprzedaży.

Bibliografia: 1. Notatki do wykładów S. Dziembowskiego, spisane przez różne osoby. 2. „Lecture Notes on Cryptography” S. Goldwasser i M. Bellare. 3. „Kryptografia dla praktyków” B. Schneier 4. „A Provably Secure Oblivious Transfer Protocol” R. Berger, R. Peralta i T. Tedrick Błędów w slajdach jest na pewno bardzo dużo. Niestety jedyną nagrodą za ich wskazanie może być zadowolenie z własnej spostrzegawczości . 31 marca 2004 Wojtek Ruszczewski (wr 181290@students. mimuw. edu. pl)