 z O x y
z O x y
 z h O x y
z h O x y
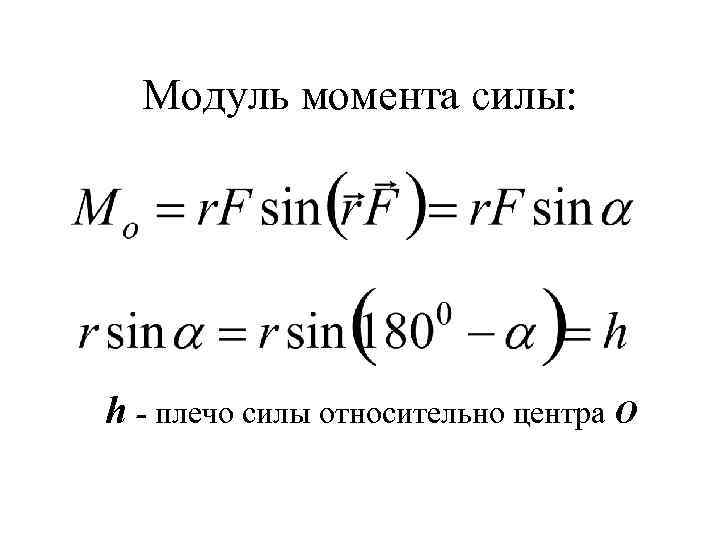 Модуль момента силы: h - плечо силы относительно центра О
Модуль момента силы: h - плечо силы относительно центра О
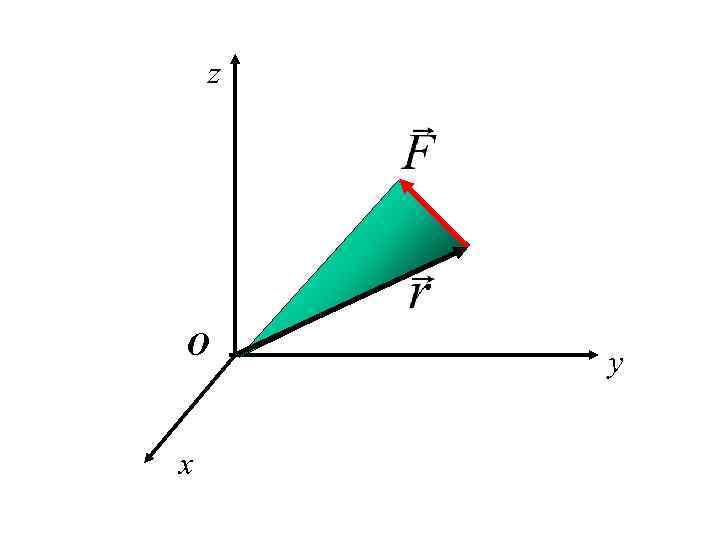
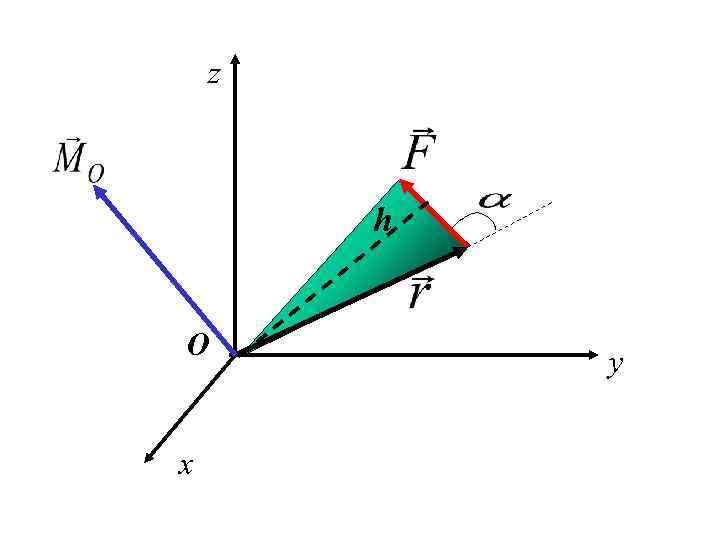
 Определение: Моментом силы относительно центра О называется вектор, приложенный к центру О, направленный перпендикулярно плоскости, образованной векторами и по правилу правого винта
Определение: Моментом силы относительно центра О называется вектор, приложенный к центру О, направленный перпендикулярно плоскости, образованной векторами и по правилу правого винта
 Порядок вычисления момента силы относительно оси: 1. Спроецировать силу на какую-либо плоскость, перпендикулярную данной оси 2. Определить кратчайшее расстояние от точки пересечения оси с плоскостью проекции до линии действия проекции силы (плечо силы относительно оси h)
Порядок вычисления момента силы относительно оси: 1. Спроецировать силу на какую-либо плоскость, перпендикулярную данной оси 2. Определить кратчайшее расстояние от точки пересечения оси с плоскостью проекции до линии действия проекции силы (плечо силы относительно оси h)
 3. Вычислить модуль момента силы по формуле 4. Определить знак момента силы - по правилу буравчика (правого винта) - или по правилу часовых стрелок
3. Вычислить модуль момента силы по формуле 4. Определить знак момента силы - по правилу буравчика (правого винта) - или по правилу часовых стрелок
 Момент силы относительно оси равен нулю если: • сила параллельна оси (в этом случае равен нулю модуль проекции силы на плоскость, перпендикулярную оси: Fxy = 0); • линия действия силы пересекает ось (в этом случае линия действия проекции силы на плоскость, перпендикулярную оси, также пересекает эту ось и плечо этой проекции равно нулю: h = 0).
Момент силы относительно оси равен нулю если: • сила параллельна оси (в этом случае равен нулю модуль проекции силы на плоскость, перпендикулярную оси: Fxy = 0); • линия действия силы пересекает ось (в этом случае линия действия проекции силы на плоскость, перпендикулярную оси, также пересекает эту ось и плечо этой проекции равно нулю: h = 0).
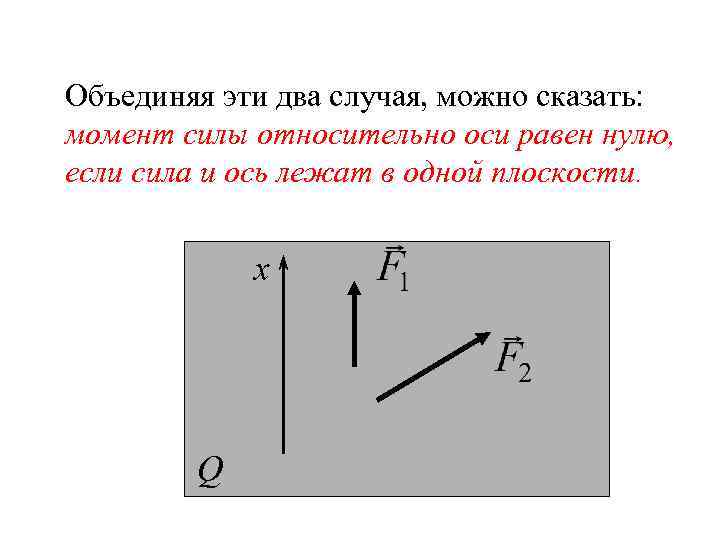 Объединяя эти два случая, можно сказать: момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости. x Q
Объединяя эти два случая, можно сказать: момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости. x Q
 • Парой сил называется система двух равных по модулю антипараллельных сил, приложенных к твердому телу. Q
• Парой сил называется система двух равных по модулю антипараллельных сил, приложенных к твердому телу. Q
 Расстояние между линиями действия сил называется плечом пары d d Q
Расстояние между линиями действия сил называется плечом пары d d Q
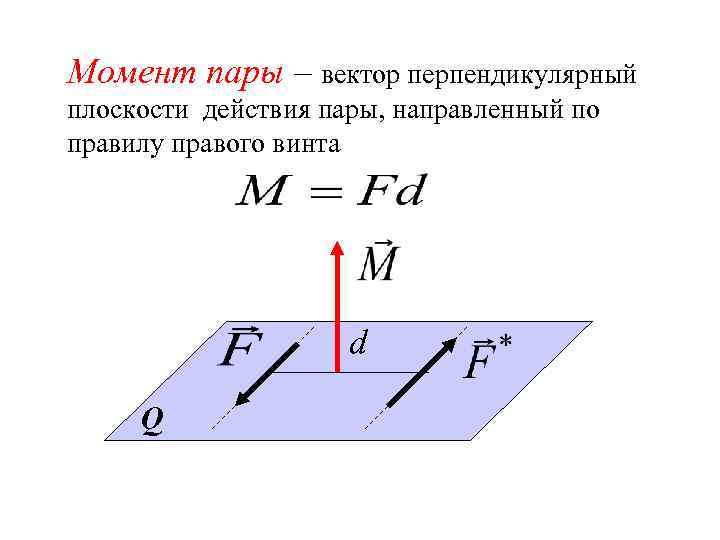 Момент пары – вектор перпендикулярный плоскости действия пары, направленный по правилу правого винта d Q
Момент пары – вектор перпендикулярный плоскости действия пары, направленный по правилу правого винта d Q
 Свойства момента пары сил: • Момент пары сил – свободный вектор, то есть его можно переносить как по линии действия, так и параллельно самому себе. Таким образом, вектор момента пары может быть приложен в любой точке твердого тела.
Свойства момента пары сил: • Момент пары сил – свободный вектор, то есть его можно переносить как по линии действия, так и параллельно самому себе. Таким образом, вектор момента пары может быть приложен в любой точке твердого тела.
 • Теорема 1 Действие пары на АТТ не изменится, если переместить пару в другое положение в плоскости ее действия
• Теорема 1 Действие пары на АТТ не изменится, если переместить пару в другое положение в плоскости ее действия
 Теорема 2 Действие пары на АТТ не изменится, если плоскость ее действия перенести параллельно самой себе
Теорема 2 Действие пары на АТТ не изменится, если плоскость ее действия перенести параллельно самой себе
 Теорема 3 Действие пары на АТТ не изменится, если любым способом видоизменить силы и плечо пары, сохраняя постоянным их произведение, т. е момент пары.
Теорема 3 Действие пары на АТТ не изменится, если любым способом видоизменить силы и плечо пары, сохраняя постоянным их произведение, т. е момент пары.
 • Система пар, действующих на АТТ, эквивалентна одной паре, момент которой равен векторной сумме моментов пар
• Система пар, действующих на АТТ, эквивалентна одной паре, момент которой равен векторной сумме моментов пар
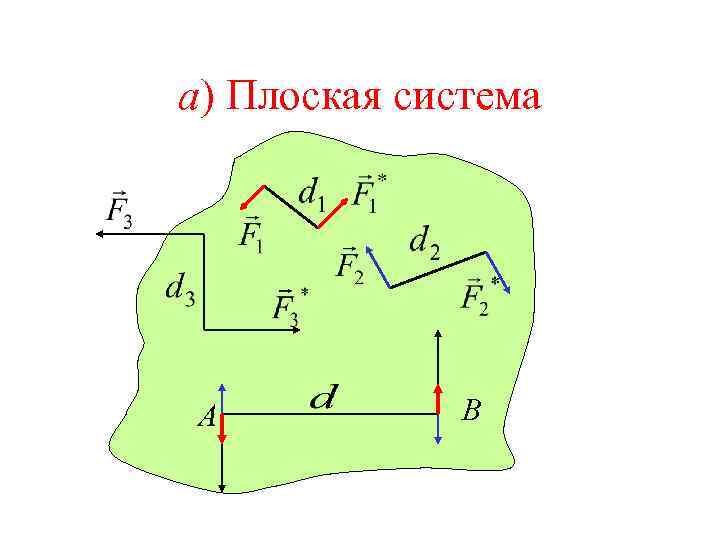 а) Плоская система А В
а) Плоская система А В
 Плоская система пар эквивалентна одной паре, момент которой равен алгебраической сумме моментов этих пар.
Плоская система пар эквивалентна одной паре, момент которой равен алгебраической сумме моментов этих пар.
 б) Пространственная система пар эквивалентна одной паре, момент которой равен векторной сумме моментов этих пар.
б) Пространственная система пар эквивалентна одной паре, момент которой равен векторной сумме моментов этих пар.