З Д КОПАЛИАНИ ОСНОВЫ ГИДРОЛОГО-МОРФОЛОГИЧЕСКОЙ ТЕОРИИ РУСЛОВОГО ПРОЦЕССА

З. Д. КОПАЛИАНИ ОСНОВЫ ГИДРОЛОГО-МОРФОЛОГИЧЕСКОЙ ТЕОРИИ РУСЛОВОГО ПРОЦЕССА. МЕТОДЫ РАСЧЕТА И ПРОГНОЗА РУСЛОВЫХ ДЕФОРМАЦИЙ. Курсы повышения квалификации специалистовгидрологов Росгидромета. 23 июня-5 июля 2008 г.

Авария на переходе магистрального трубопровода через р. Волгу в районе г. Астрахани

Авария на переходе магистрального трубопровода через р. Белую

Деформации русла р. Самары за 1954 -96 гг. и оголение трубопровода в створе ПП МН «Ромашкино-Куйбыше» . 1. Ошибка в прогнозируемом профиле предельного размыва 2, Укладка трубопровода выше профиля предельного размыва

Экспертиза проектов переходов через реки (русловой аспект) Результаты строительства подводного перехода трубопровода через малую реку без учета ее плановых деформаций

В. М. Лохтин, 1897 г. «Поменьше формул и побольше наблюдательности» Н. С. Лелявский «Несмотря на обширные работы многих математиков, гидродинамика не дала еще ни одной точной формулы, безусловно приложимой к практическим расчетам»

Н. Е. Кондратьев, 1972 г. Иногда под теорией понимают не полноту охвата явления логическими связями, а развитость математического аппарата. Но самой наукой математика остается лишь там, где кроме нет другой науки. В прочих же науках она только язык науки… Непонимание этого положения иногда приводит к развитию математического пустословия, которое не только существует, но и вызывает восхищение тех, кто склонен умиляться непонятному. Слабым местом современной теории руслового процесса является недостаточная изученность самого процесса и отсутствие основных формулировок, отражающих его сущность. Отсюда противоречия в разработке деталей, дискуссии по форме, при потере интереса к строгости исходных позиций. Отсюда же и несколько преувеличенный интерес к аппарату, которым подменяется теория.

А. Раудкиви, 1999 г. «… агрессивно наступает рынок математических моделей по проблеме русел с подвижным дном. Модельеры преимущественно являются специалистами по программированию и компьютерам с ограниченными знаниями в области физики процессов, происходящих в руслах с подвижными границами. Но красочный продукт компьютерного искусства производит гипнотизирующее воздействие на многих заказчиков особенно из управленческой среды. Конечная продукция при этом не является вкладом ни в компьютерную науку, ни в понимание физики процессов на границе раздела двух сред: потока и подвижного русла. Вызывает озабоченность, что во всем мире сегодня так мало людей занимается исследованием этой сложной и увлекательной проблемы»

Традиционные задачи, вытекающие из логики развития знаний о речном русле и русловом процессе: • Развитие общей теории руслового процесса, методов расчета и прогноза русловых деформаций, расчета расхода и стока наносов в реках, гидравлических сопротивлений; • Развитие теории и практики гидравлического моделирования, математического и гибридного моделирования руслового процесса; • Широкомасштабные натурные исследования расхода наносов, механизм размыва берегов меандрирующих рек, динамики речных перекатов; • Инженерные и природоохранные аспекты теории руслового процесса и его приложений; • Взаимодействие с инженерными сооружениями и мероприятиями, охрана, восстановление и мониторинг речных русел и пойм, создание методов управления русловым процессом, разработка нормативных документов;

Интеграция и синтез достижений теории руслового процесса и ее прикладных аспектов с другими областями знаний: • Гидрометрия: учет руслового процесса и его типов в речной гидрометрии при выборе измерительных створов и подсчете стока (выход воды на пойму, учет гидравлических сопротивлений русловых форм при интерполяции и экстраполяции кривых Q= f(H); • Гидрофизика: русловые аспекты наводнений и формирования ледовых заторов на реках, а также методов борьбы с ними; • Экология: широкий круг вопросов, связанных с оценкой причин и последствий ухудшения экологических условий при нарушении естественного режима руслового процесса в результате хозяйственного использования речных русел и пойм и разработкой рекомендаций по предотвращению и ликвидации негативных последствий • Теория формирования и расчеты стока: создание новых и вспомогательных методов расчета характеристик стока воды при недостатке или отсутствии данных гидрометеорологических наблюдений на основе структурных гидроморфологических зависимостей и гидрологических обобщений; • Климатология: задача изучения чувствительности гидрографической сети и речных русел (метаморфоза типов руслового процесса, режима русловых деформаций), к изменениям климата. Разработка стратегии адаптации руслового процесса к изменениям климата (инженерной инфраструктуры, условий судоходства, восстановление и охрана речных русел).

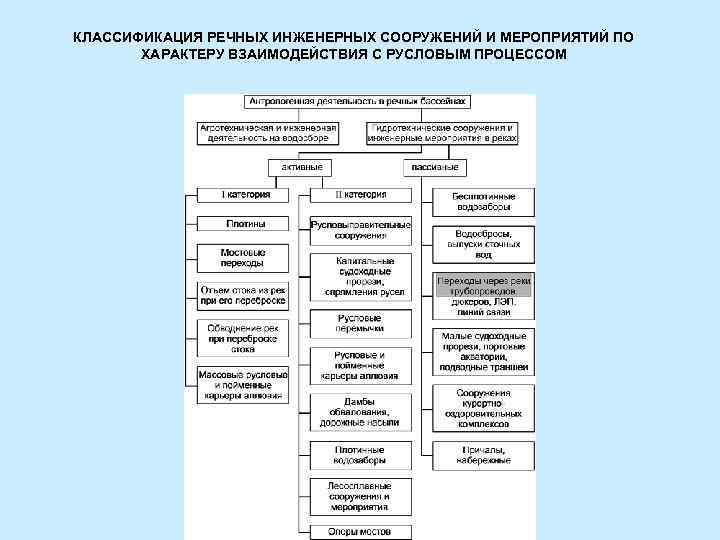КЛАССИФИКАЦИЯ РЕЧНЫХ ИНЖЕНЕРНЫХ СООРУЖЕНИЙ И МЕРОПРИЯТИЙ ПО ХАРАКТЕРУ ВЗАИМОДЕЙСТВИЯ С РУСЛОВЫМ ПРОЦЕССОМ

Гидравлическая модель р. Иртыш с размываемым дном

Кривая z 0=f(Q)по данным экспериментов на 82 метровом лотке при различных состояниях дна 1 -гладкое (безгрядовое дно), 2 -микроформы, 3 -побочни с микроформами, 4 -побочни без микроформ

Характеристики пропускной способности русла с побочнями о данным экспериментов в 82 -метровом лотке Состояние дна Z 0, см Qi, л/с Qi / Q 3 2 3 4 5 Гладкое 20, 50 2, 69 45, 00 1, 76 С микроформами 14, 50 1, 91 36, 00 1, 41 С побочнями и микроформами 7, 60 1, 00 25, 50 1, 00 С побочнями без микроформ 19, 25 2, 53 42, 00 1, 65 1

Гидравлические сопротивления при грядовом строении дна • CГ = 0. 019 v. Fr 3 • CГ = 0. 009 v (v/v 0)2(hг/d)-0. 8 • q. T = 0. 011 v hг. Fr 3 • μ = 0. 011 hг. Fr 3/H • C/√g = 0. 78(v/v 0)0. 7(d/hг)0. 27 I-0. 5 • C/√g = 4. 4(H/hг)0. 33μ 0. 33 I-0. 5 (6) • λ = 3. 28 I/[(v/v 0)1. 14(d/hг)0. 54] (7) • λ = 0. 1(H/hг)-0. 67μ-0. 67 I (1) (2) (3) (4) (5) (8)

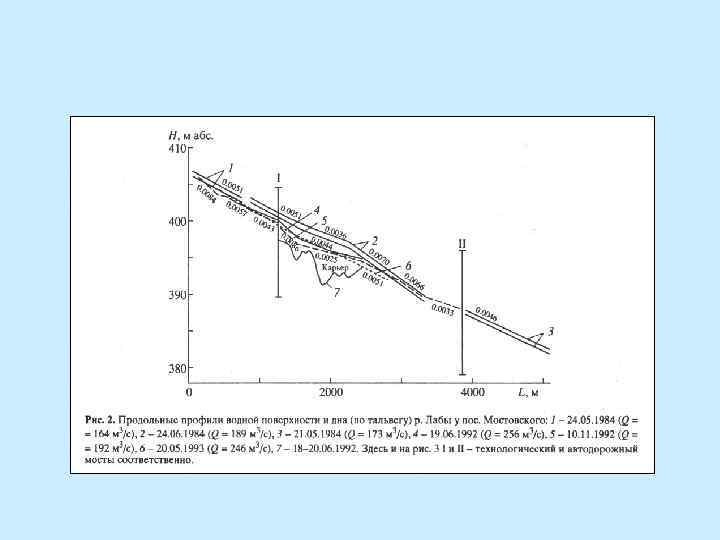
Продольные профили дна и свободной поверхности воды Нижней Кубани

ОСНОВНЫЕ ПОЛОЖЕНИЯ (ПОСТУЛАТЫ) ГИДРОЛОГО-МОРФОЛОГИЧЕСКОЙ ТЕОРИИ РУСЛОВОГО ПРОЦЕССА ПОД РУСЛОВЫМ ПРОЦЕССОМ ПОНИМАЮТСЯ ИЗМЕНЕНИЯ В МОРФОЛОГИЧЕСКОМ СТРОЕНИИ РЕЧНОГО РУСЛА И ПОЙМЫ, ПРОИСХОДЯЩИЕ ПОД ДЕЙСТВИЕМ ТЕКУЩЕЙ ВОДЫ. ВСЕ ВИДЫ РЕЧНЫХ ДЕФОРМАЦИЙ ПОДРАЗДЕЛЯЮТ НА НЕОБРАТИМЫЕ И ОБРАТИМЫЕ. В ПЕРВЫХ ВЫРАЖАЕТСЯ ВЕКОВОЙ ХОД РАЗВИТИЯ РЕКИ, ВО ВТОРЫХ - ТРАНСПОРТ НАНОСОВ. В САМЫХ ВЕРХОВЬЯХ РЕК И В ПЕРИФЕРИЙНЫХ ЗВЕНЬЯХ ЕЕ ПРИТОКОВ НАБЛЮДАЮТСЯ ЭРОЗИОННЫЕ ПРОЦЕССЫ. В РЕЧНЫХ ДЕЛЬТАХ ПРОИСХОДИТ АККУМУЛЯЦИЯ НАНОСОВ ЭРОЗИОННЫЕ И АККУМУЛЯТИВНЫЕ ПРОЦЕССЫ НЕОБРАТИМЫ. В ОСНОВНОЙ ЧАСТИ РЕЧНОЙ СИСТЕМЫ ПРОИСХОДИТ ПЕРЕОТЛОЖЕНИЕ НАНОСОВ, В ПРОЦЕССЕ КОТОРОГО ЭРОЗИЯ СМЕНЯЕТСЯ АККУМУЛЯЦИЕЙ И ОБРАТНО. ЭТО ВЫРАЖАЕТСЯ В ОБРАЗОВАНИИ И ИСЧЕЗНОВЕНИИ АЛЛЮВИАЛЬНЫХ ФОРМ В ПОПЕРЕЧНОМ СЕЧЕНИИ РУСЛА И В ПЛАНОВЫХ ЦИКЛИЧЕСКИХ ПЕРЕМЕЩЕНИЯХ РУСЛА В ПОЙМЕ. ЭТИ ПРОЦЕССЫ ОБЛАДАЮТ СВОЙСТВОМ ОБРАТИМОСТИ. ПОСКОЛЬКУ РУСЛОВЫЕ ДЕФОРМАЦИИ НЕРАЗРЫВНО СВЯЗАНЫ С ТРАНСПОРТОМ НАНОСОВ, А ТРАНСПОРТ НАНОСОВ НЕ ОСУЩЕСТВИМ БЕЗ РУСЛОВЫХ ИЛИ ПОЙМЕННЫХ ДЕФОРМАЦИЙ, ТО РУСЛОВОЙ ПРОЦЕСС СЛЕДУЕТ СЧИТАТЬ ФОРМОЙ ТРАНСПОРТА НАНОСОВ, А ПРОЦЕСС ТРАНСПОРТА НАНОСОВ – ВНУТРЕННИМ СОДЕРЖАНИЕМ РУСЛОВЫХ ДЕФОРМАЦИЙ.

ПО ФОРМЕ ДВИЖЕНИЯ НАНОСЫ ПОДРАЗДЕЛЯЮТСЯ НА ВЗВЕШЕННЫЕ И ДОННЫЕ НАНОСЫ В ОСНОВНОМ СЛАГАЮТ РУСЛО, ВЗВЕШЕННЫЕ ПРЕОБЛАДАЮТ В ТВЕРДОМ СТОКЕ И В ОСНОВНОМ СЛАГАЮТ ПОЙМУ. - СОСТОЯНИЕ РЕКИ, ПРИ КОТОРОМ ОБНАРУЖИВАЮТСЯ ТОЛЬКО ОБРАТИМЫЕ ДЕФОРМАЦИИ, Т. Е. ВСЕ ДЕФОРМАЦИИ ОПРЕДЕЛЯЮТСЯ ТРАНЗИТОМ НАНОСОВ, НАЗЫВАЕТСЯ СОСТОЯНИЕМ ДИНАМИЧЕСКОГО РАВНОВЕСИЯ. В ЭТОМ СОСТОЯНИИ ПРЕБЫВАЮТ БОЛЬШИНСТВО ТРАНЗИТНЫХ УЧАСТКОВ РЕК С НЕНАРУШЕННЫМ ВОДНЫМ РЕЖИМОМ. -РУСЛОВОЙ ПРОЦЕСС ОБЛАДАЕТ ОБЩЕЙ УСТОЙЧИВОСТЬЮ, КОТОРАЯ ВЫРАЖАЕТСЯ В ТОМ, ЧТО ПРИ УВЕЛИЧЕНИИ ИЛИ УМЕНЬШЕНИИ ТВЕРДОГО СТОКА, ВЫВОДЯЩЕМ РЕКУ ИЗ СОСТОЯНИЯ ДИНАМИЧЕСКОГО РАВНОВЕСИЯ, ПРОИСХОДИТ ТАКАЯ ВНУТРЕННЯЯ ПЕРЕСТРОЙКА РУСЛА И ПОЙМЫ, ПРИ КОТОРОЙ ДИНАМИЧЕСКОЕ РАВНОВЕСИЕ ВОССТАНАВЛИВАЕТСЯ. ИНЫМИ СЛОВАМИ, РЕКА ОБЛАДАЕТ СПОСОБНОСТЬЮ В ВЕСЬМА ШИРОКИХ ПРЕДЕЛАХ ИЗМЕНЯТЬ СВОЮ ТРАНСПОРТИРУЮЩУЮ СПОСОБНОСТЬ В ЗАВИСИМОСТИ ОТ ЗАДАННОГО ЕЙ ОБЪЕМА ТВЕРДОГО СТОКА. ЭТО ДОСТИГАЕТСЯ ИЗМЕНЕНИЕМ ИЗВИЛИСТОСТИ РУСЛА (УКЛОНА), ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ И СОДЕРЖАНИЯ ВЗВЕШЕННЫХ НАНОСОВ В ДОННЫХ ОТЛОЖЕНИЯХ СПОСОБНОСТЬ РЕКИ К САМОРЕГУЛИРОВАНИЮ ПОЗВОЛЯЕТ ВЫДЕЛИТЬ В КАЧЕСТВЕ ОСНОВНЫХ СЛЕДУЮЩИЕ НЕЗАВИСИМЫЕ ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ ТИП РУСЛОВОГО ПРОЦЕССА: ПОЛНЫЕ ХАРАКТЕРИСТИКИ СТОКА ВОДЫ; ПОЛНЫЕ ХАРАКТЕРИСТИКИ СТОКА НАНОСОВ И УСЛОВИЯ, ОГРАНИЧИВАЮЩИЕ СВОБОДНОЕ РАЗВИТИЕ РУСЛОВОГО ПРОЦЕССА (ВЫХОДЫ НЕРАЗМЫВАЕМЫХ ПОРОД В РУСЛЕ, ОБЩИЙ И МЕСТНЫЙ БАЗИСЫ ЭРОЗИИ).

• - ДИСКРЕТНЫЕ ПОДХОД ПОЗВОЛЯЮТ ПРЕДСТАВИТЬ ОСНОВНОЕ СОДЕРЖАНИЕ РУСЛОВОГО ПРОЦЕССА – ТРАНСПОРТ НАНОСОВ КАК СТРОГО ОРГАНИЗОВАННЫЙ ПРОЦЕСС, В КОТОРОМ МОЖНО ВЫДЕЛИТЬ НЕСКОЛЬКО СТРУКТУРНЫХ УРОВНЕЙ. НА КАЖДОМ ИЗ ЭТИХ УРОВНЕЙ ДЕЙСТВУЕТ СВОЙ ЗАКОН И РЕШАЮТСЯ СВОИ ПРАКТИЧЕСКИЕ ЗАДАЧИ • КАЖДЫЙ ПОСЛЕДУЮЩИЙ СТРУКТУРНЫЙ УРОВЕНЬ СОДЕРЖИТ ПРЕДЫДУЩИЕ. НАИНИЗШЕЙ СТРУКТУРНОЙ СТУПЕНЬЮ ЯВЛЯЕТСЯ ДВИЖЕНИЕ ОТДЕЛЬНОЙ ЧАСТИЦЫ В ПОТОКЕ. ЗАТЕМ ВЫДЕЛЯЕТСЯ СТРУКТУРНЫЙ УРОВЕНЬ МИКРОФОРМ – МЕЛКИХ ПЕСЧАНЫХ ГРЯД МАССОВОГО РАСПРОСТРАНЕНИЯ, СОИЗМЕРИМЫХ С ГЛУБИНОЙ РУСЛА, НО НЕ ВЫРАЖАЮЩИХ ЕГО МОРФОЛОГИЮ. МИКРОФОРМЫ ВОСПРИНИМАЮТСЯ КАК МАКРОШЕРОХОВАТОСТЬ. ОНИ ОПРЕДЕЛЯЮТ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ ПОТОКА И ВЫРАЖАЮТ РАСХОД ДОННЫХ НАНОСОВ. СЛЕДУЮЩИЙ СТРУКТУРНЫЙ УРОВЕНЬ – МЕЗОФОРМЫ, ПРЕДСТАВЛЯЮТ СОБОЙ КРУПНЫЕ ПЕСЧАНЫЕ СКОПЛЕНИЯ В РУСЛЕ, СОИЗМЕРИМЫЕ С ЕГО ШИРИНОЙ И ОПРЕДЕЛЯЮЩИЕ ОБЩИЙ МОРФОЛОГИЧЕСКИЙ ОБЛИК РУСЛА. МЕЗОФОРМЫ ОБЛАДАЮТ БОЛЬШЕЙ ПО СРАВНЕНИЮ С МИКРОФОРМАМИ ИНЕРЦИОННОСТЬЮ. В СЛЕДУЮЩЕМ СТРУКТУРНОМ УРОВНЕ – МАКРОФОРМАХ – ПРОЯВЛЯЕТСЯ ПОЛНЫЙ КОМПЛЕКС МОРФОЛОГИЧЕСКИХ ЭЛЕМЕНТОВ РЕКИ, ОХВАТЫВАЮЩИЙ РУСЛО И ПОЙМУ И ВЫРАЖАЮЩИЙСЯ В ТИПЕ РУСЛОВОГО ПРОЦЕССА. УЧАСТОК РЕКИ, В ПРЕДЕЛАХ КОТОРОГО НЕ МЕНЯЮТСЯ ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ РУСЛОВОЙ ПРОЦЕСС И ПОЭТОМУ РАЗВИТ ОДИН, ОПРЕДЕЛЕННЫЙ ТИП РУСЛОВОГО ПРОЦЕССА, НАЗЫВАЕТСЯ МОРФОЛОГИЧЕСКИ ОДНОРОДНЫМ УЧАСТКОМ. • •

Типизация руслового процесса ГГИ

ИЗМЕРИТЕЛИ ТИПОВ РУСЛОВОГО ПРОЦЕССА – шаг излучин, расстояние по прямой линии между точками перегиба русла – шаг русловых мезоформ, расстояние по средней линии русла, между гребнями двух следующих друг за другом ленточных гряд ) ( ); побочней ( ); осерёдков ( – угол разворота излучины (сумма углов входа и выхода излучины – угол входа излучины и угол выхода – углы, образованные касательной к точке перегиба и прямой, соединяющей смежные точки перегиба, располагающиеся соответственно в верховой и низовой частях излучины.

1 - русловая многорукавность 2 - незавершенное меандрирование 3 – свободное меандрирование 4 – пойменная многорукавность Уклон дна долины Зависимость типов руслового процесса от уклона долины и средней водности паводков Средний из годовых максимумов расхода воды, м 3/с

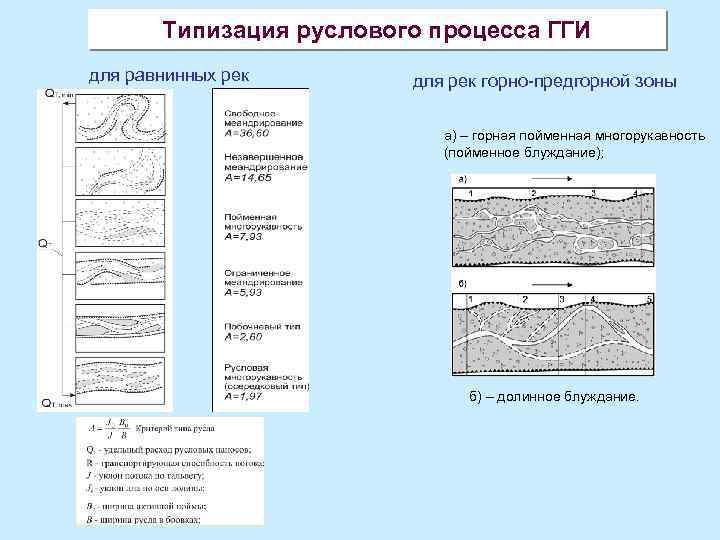Типизация руслового процесса ГГИ для равнинных рек для рек горно-предгорной зоны а) – горная пойменная многорукавность (пойменное блуждание); б) – долинное блуждание.

Генетическая диаграмма типов руслового процесса рек бассейна Кубани

Изменения максимальных расходов воды за период наблюдений на реках бассейна Кубани

Плановые деформации русла р. Кубани у г. Новокубанска

Плановые деформации русла р. Лабы в нижнем течении

РАСПРОСТРАНЕНИЕ ТИПОВ РУСЛОВОГО ПРОЦЕССА НА ТЕРРИТОРИИ БАССЕЙНА Р. КУБАНЬ

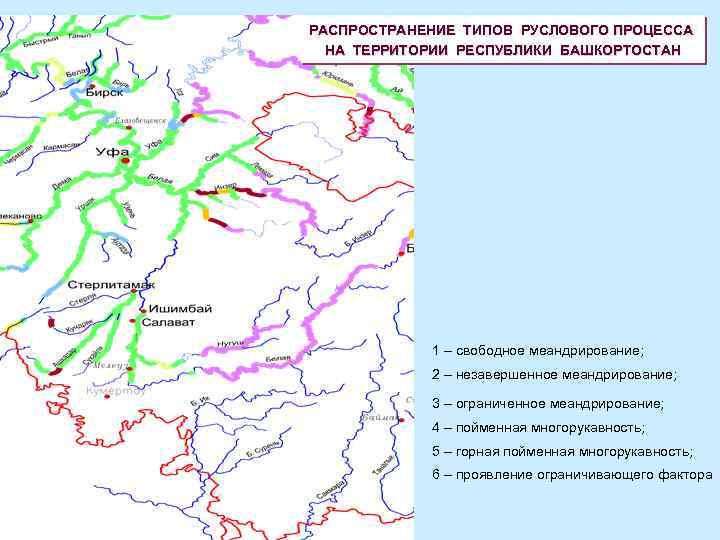РАСПРОСТРАНЕНИЕ ТИПОВ РУСЛОВОГО ПРОЦЕССА НА ТЕРРИТОРИИ РЕСПУБЛИКИ БАШКОРТОСТАН 1 – свободное меандрирование; 2 – незавершенное меандрирование; 3 – ограниченное меандрирование; 4 – пойменная многорукавность; 5 – горная пойменная многорукавность; 6 – проявление ограничивающего фактора

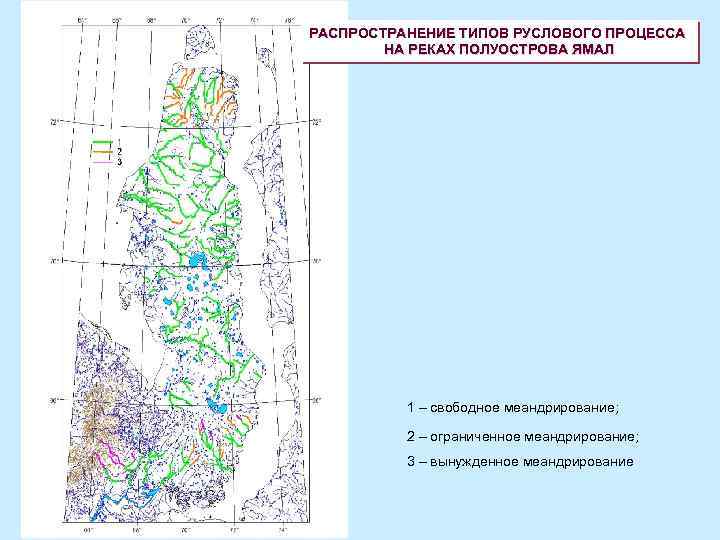РАСПРОСТРАНЕНИЕ ТИПОВ РУСЛОВОГО ПРОЦЕССА НА РЕКАХ ПОЛУОСТРОВА ЯМАЛ 1 – свободное меандрирование; 2 – ограниченное меандрирование; 3 – вынужденное меандрирование

СКОРОСТЬ ПЛАНОВЫХ ДЕФОРМАЦИЙ ВОГНУТЫХ БЕРЕГОВ СВОБОДНО МЕАНДРИРУЮЩИХ РЕК ПВА ЯМАЛ Река Участок, км от устья Скорость размыва берега, С, м/год максимальная среднемноголетняя Qмакс, 1% Уклон водной пов-сти, I, ‰ 3, 6 -4, 1 1, 5 -2, 8 - - р. Хальмарьяха 1, 4 0, 7 -0, 8 - - р. Сил-Яха 2, 4 0, 6 -1, 4 - - р. Надуй-Яха 1, 8 -2, 1 0, 6 -1, 3 - - р. Сеяха 1, 8 -2, 1 0, 7 -1, 6 - - р. Тесю-Се 0, 9 -1, 0 0, 5 -0, 8 - - ПП ГП 2, 0 0, 6 -1, 0 - - 193 км 3, 6 1078 - 297 км 1, 6 220 - 268 км – мост 0, 9 1100 - 2, 5 445 0, 1 304 км 4, 6 1410 0, 7 мостовой переход 1, 3 2522 131, 6 км 4, 0 294 ПП ГП 2, 0 1358 ПП ГП 3, 9 1, 2 -1, 4 2620 0, 19 мостовой переход 1, 4 1, 6 0, 7 -1, 7 0, 6 -1, 1 3250 799 0, 05 р. Харасовая р. Ензорьяха р. Хэяха р. Яяха р. Еркатаяха р. Ясавей-Яха р. Юрибей р. Щучья ПП ГП мостовой переход 1, 0 0, 17

ОЦЕНКА ФОРМ ТРАНСПОРТА НАНОСОВ В РЕКАХ Для оценки форм транспорта наносов в реках (влечение, сальтация, взвешивание) и их учёта при расчётах заносимости подводных траншей на переходах трубопроводов следует пользоваться формулами характерных значений вертикальной компоненты пульсационной скорости потока: - осреднённое во времени и по глубине потока значение вертикальной компоненты -наибольшее возможное при данном гидравлическом режиме значение вертикальной компоненты в зоне (0, 15 0, 40)Н от дна потока - динамическая скорость

Форма движения наносов устанавливается путём сопоставления гидравлической крупности частиц с характерными значениями вертикальной компоненты Если где u – гидравлическая крупность, наносы перемещаются в форме влечения по дну Если наносы перемещаются в форме сальтации вблизи дна Если сальтирующие частицы достигают середины глубины потока. Если наносы переходят во взвешенное состояние и распространяются на всю глубину потока.

ГИДРАВЛИЧЕСКАЯ КРУПНОСТЬ ЧАСТИЦ НАНОСОВ , М/С. Приведённый диаметр d, мм Температура t, °С 00 100 200 300 0, 030 0, 000451 0, 000617 0, 00080 0, 000999 0, 040 0, 000800 0, 00109 0, 00141 0, 00176 0, 050 0, 000125 0, 00168 0, 00219 0, 00271 0, 075 0, 00276 0, 00371 0, 00469 0, 00569 0, 100 0, 00476 0, 00625 0, 00774 0, 00912 0, 125 0, 00713 0, 00914 0, 0110 0, 01275 0, 150 0, 00971 0, 01217 0, 0143 0, 0165 0, 175 0, 01241 0, 0152 0, 0178 0, 0202 0, 20 0, 01518 0, 0184 0, 0213 0, 0241 0, 30 0, 0266 0, 0315 0, 0360 0, 0400 0, 40 0, 0385 0, 0452 0, 0507 0, 0555 0, 0508 0, 0584 0, 0646 0, 0694 0, 7 0, 0745 0, 0822 0, 0890 0, 0943 0, 9 0, 0953 0, 1038 0, 1102 0, 1143 1, 0 0, 1045 0, 1129 0, 1196 0, 1237 1, 4 0, 139 0, 146 0, 151 0, 154 1, 8 0, 167 0, 173 0, 178 0, 180 2, 0 0, 185 0, 189 0, 190

Диаграмма форм транспорта донных отложений

ЗНАЧЕНИЯ НЕРАЗМЫВАЮЩИХ СКОРОСТЕЙ ПОТОКА ДЛЯ ПЕСЧАНЫХ МАТЕРИАЛОВ, М/С Глубина потока Н, м 0, 1 0, 2 0, 3 0, 4 0, 5 1, 0 2 4 6 8 10 0, 5 0, 37 0, 38 0, 39 0, 40 0, 43 0, 48 0, 54 0, 60 0, 64 0, 68 1, 0 0, 43 0, 44 0, 45 0, 46 0, 49 0, 55 0, 63 0, 69 0, 74 0, 78 2, 0 0, 49 0, 50 0, 51 0, 52 0, 53 0, 57 0, 63 0, 72 0, 80 0, 85 0, 90 3, 0 0, 53 0, 54 0, 56 0, 57 0, 62 0, 68 0, 78 0, 86 0, 92 0, 98 4, 0 0, 56 0, 58 0, 59 0, 60 0, 61 0, 65 0, 71 0, 82 0, 91 0, 98 1, 04 5, 0 0, 59 0, 60 0, 62 0, 63 0, 68 0, 76 0, 86 0, 96 1, 02 1, 08 6, 0 0, 61 0, 62 0, 64 0, 65 0, 66 0, 71 0, 78 0, 89 0, 99 1, 06 1, 12 7, 0 0, 63 0, 64 0, 66 0, 67 0, 68 0, 73 0, 81 0, 92 1, 02 1, 10 1, 16 8, 0 0, 65 0, 66 0, 68 0, 69 0, 70 0, 75 0, 83 0, 95 1, 05 1, 12 1, 19 9, 0 0, 66 0, 68 0, 69 0, 70 0, 71 0, 77 0, 85 0, 97 1, 08 1, 14 1, 22 10, 0 0, 68 0, 69 0, 71 0, 72 0, 73 0, 78 0, 87 0, 99 1, 10 1, 18 1, 25 12, 0 0, 72 0, 73 0, 74 0, 76 0, 81 0, 90 1, 03 1, 14 1, 22 1, 29 15, 0 0, 74 0, 75 0, 76 0, 78 0, 79 0, 85 0, 94 1, 08 1, 19 1, 28 1, 36 17, 0 0, 75 0, 77 0, 78 0, 80 0, 81 0, 87 0, 96 1, 11 1, 22 1, 30 1, 38 20, 0 0, 78 0, 80 0, 81 0, 82 0, 84 0, 90 1, 00 1, 14 1, 26 1, 35 1, 43 Диаметр частиц d, мм

Значения неразмывающей скорости потока м/с для крупных наносов Диаметр частиц d, мм H, м 15 20 30 40 50 70 100 150 200 250 300 400 500 600 0. 5 1. 12 1. 23 1. 41 1. 52 1. 62 1. 75 1. 88 1. 97 2. 00 - - 1. 0 1. 25 1. 40 1. 60 1. 76 1. 88 2. 07 2. 30 2. 50 2. 67 2. 74 2. 78 2. 80 - 1. 5 1. 34 1. 47 1. 71 1. 88 2. 03 2. 25 2. 52 2. 83 3. 02 3. 14 3. 27 3. 34 3. 43 3. 47 2. 0 1. 38 1. 54 1. 79 1. 98 2. 22 2. 37 2. 66 3. 00 3. 26 3. 42 3. 54 3. 74 3. 90 3. 92 2. 5 1. 42 1. 58 1. 85 2. 10 2. 33 2. 47 2. 80 3. 17 3. 41 3. 63 3. 70 4. 00 4. 21 4. 28 3. 0 1. 46 1. 62 1. 90 2. 12 2. 38 2. 65 2. 87 3. 28 3. 58 3. 80 4. 00 4. 22 4. 45 4. 60 4. 0 1. 51 1. 68 1. 95 2. 19 2. 40 2. 71 3. 22 3. 43 3. 80 4. 06 4. 25 4. 56 4. 86 5. 00

Оценка характеристик транспорта наносов и деформаций русел и пойм рек §при траншейном способе прокладки трубопровода и методе наклонного бурения. Расчёты подвижности руслового аллювиального материала, характеристик русловых микроформ и расхода донных наносов

Диаграмма форм транспорта донных отложений

Интегральная кривая трансостава (а) пробы донных отложений (б) на участке гидрологического поста р. Б. Зеленчук-ст. Зеленчукская

Обеспеченность расходов воды, соответствующих критическим фазам движения частиц наносов Обеспеченность Qнач движения Кубань -Армавир Б. Зеленчук - Зеленчукская 746 177 64% d 50 210 91% d 15 631 318 46 d 50 334 d 25 <80 657 47% d 85 250 98% 159 dmax Кубань Успенское в ряду максимальных расходов dmax 448 Qнач движения м 3/с d 50 Кубань им. Коста Хетагурова Qmax, ср м 3/с фракция dmax Участок реки 99, 8 d 85 55 d 50 24, 9 в ряду средних годовых расходов в ряду минимальных расходов Р

Продолжительность стояния суточных расходов воды, соответствующих критическим фазам движения частиц наносов Продолжительность стояния Qнач движения Участок реки Qmax, ср фракция м 3/с Qнач движения м 3/с период наблюдений, N, сут. число случаев, m, сут. частота, Р=m|N 164 0, 0090 1315 0, 0720 8760 0, 4799 527 0, 0332 5730 0, 3607 59 0, 0032 2130 0, 1166 dmax Кубань Армавир Б. Зеленчук - Зеленчукская 746 177 46 d 50 334 d 25 <80 657 d 85 250 159 4620 0, 2530 dmax 631 210 d 50 Кубань Успенское d 50 dmax 448 318 d 15 Кубань им. Коста Хетагурова 99, 8 284 0, 0156 d 85 55 3200 0, 1761 d 50 24, 9 7700 0, 4237 18254 15885 18264 18174

Прогноз переформирования русла в нижнем бъефе плотины Чепетон на р. Парана при использовании формул разных исследователей

Исходный массив фактических измерений расходов в реках, каналах, гидравлических лотках и на гидравлических размываемых моделях V d объект исследований H (м) (м/с) лотки 0. 01 -1. 09 0. 14 -2. 90 0. 24 -3. 50 0. 10 -0. 29 модели 0. 02 -0. 26 0. 18 -0. 69 0. 16 -1. 17 0. 22 -3. 25 каналы 0. 11 -6. 10 0. 51 -0. 88 0. 08 -0. 53 0. 10 -1. 46 горные реки 0. 09 -6. 34 0. 47 -3. 35 0. 25 -1. 18 1. 09 -116 равнинные реки 0. 11 -17. 1 0. 16 -2. 10 0. 05 -0. 50 0. 06 -9. 7 Fr (мм) Было использовано 2086 измерений расходов донных наносов: 1038 измерений при безгрядовом режиме движения частиц; 1048 измерений расходов донных наносов в грядовой форме; 911 измерений высоты гряд; 1048 измерений скорости движения гряд

Формула ГГИ

Рекомендуемые формулы для расчета расходов донных наносов в реках и земляных каналах При грядовом движении донных наносов в руслах равнинных и горно-предгорных рек Формула ГГИ: q. T= 0. 01 hг. VFr 3; м 3/c* м (1) h. Г = 0. 25 H; H<1 (2) h. Г = 0. 20 + 0. 1 H; H>1 h. Г = 0. 39 d(V/V 0)2. 5 Fr -3. 75 (3) V 0 = 3 H 0. 2(d+0. 0014)0. 3 h. Г = (0. 07 V/V 0 + 0. 02)H (4) 15

При грядовом движении донных наносов: для малых равнинных рек Формулы: ГГИ, Ю. М. Корчохи, К. В. Гришанина, А. Ф. Кудряшова, Мейер-Петера, Доу-Го-Женя, Цубаки и др. для крупных предгорных рек Зависимость Г. И. Шамова и региональные зависимости: Тимиревой-Классен Qт=7γI 3/2(Q-Q 0)2 (Q 0/Q) 0. 25 /√gdmax 2. 5; кг/c (6) В. В. Ромашина Qт=11232 ρ/ρт(Q-Q 0)1. 2/Q 00. 2 Qmx/(Qm-1)x м 3/сут Q 0=0. 067 √g(d 50/I)2. 5 (7) для земляных каналов ( условия слабого транспорта песчаного материала при малых числах Фруда: безгрядовый режим или рифели ) Формулы С. Х. Абальянца qт=0. 84 V 4 H-5/6; кг/с* м qт=0. 03 V 3(V-V 0)(Hd)-0. 25; кг/с* м (8) (9)

Расчет высоты микроформ – гряд (hг в м) При отсутствии данных о подвижности донных наносов для малых рек, сложенных из песчаного материала для средних и крупных равнинных рек: При наличии данных о глубине и скорости потока в общем виде для малых и средних рек, сложенных из гравийно-галечного материала и крупного песка в диапазоне значений относительной гладкости потока 30 Н/d 150

6. 1. 6 Скорость смещения гряд установившегося профиля определяется в м/с по формуле : или в м/сут по номограммам : Номограммы для определения скорости движения русловых микроформ по формуле

При безгрядовом движении донных наносов в руслах равнинных и горнопредгорных рек, имеющем место при неоднородном составе грунта и неполном вовлечении в движение всех фракций донных отложений (130 , в руслах равнинных и горно-предгорных рек (1. 3

6. 1. 10. Расчет удельного расхода донных наносов для мелких песчаных наносов со средним диаметром менее 0, 5 мм, перемещающихся в форме гряд при средних скоростях потока менее 1, 5 м/с рекомендуется выполнить по формуле: м 3/(сут. м) 6. 1. 11. При отсутствии данных о степени подвижности донных отложений и высоте гряд, удельный расход донных наносов на малых равнинных реках с песчаным составом грунта при грядовом движении наносов рекомендуется определять по формуле м 3/(с. м)

При наличии данных о крупности донных наносов для определения неразмывающей скорости потока V 0, расход донных наносов (q. Т в м 3/с. м) при грядовом движении наносов на малых равнинных реках определяется по формулам: при при

На малых и средних реках, сложенных из крупного песка и гравийно-галечного материала, в диапазоне значений относительной гладкости потока при наличии сведений о крупности донных отложений и гидравлических характеристиках потока, удельный расход донных наносов в грядовой форме в м 3/(с. м) рекомендуется вычислять по следующим зависимостям: При При 6. 1. 14. Полный расход донных наносов в объемном выражении (м 3/сут. ), для рек горнопредгорной зоны при структурной и бесструктурной форме их движения, в диапазоне руслоформирующих расходов воды 73 -766 м 3/с, уклонах дна 0, 004 -0, 028 и средней крупности донных отложений 0, 013 -0, 058 м, рекомендуется определять по формуле В. В. Ромашина

Полный расход донных наносов на малых горных реках при безгрядовом транспорте донных наносов всех фракций, имеющем место при уклонах дна и расходах воды обеспеченностью менее 10 относительной гладкости потока в ряду максимальных расходов, рекомендуется определять по формуле: где в м 3/с, в кг/с Для участков переходов трубопроводов через земляные каналы (условия слабого транспорта песчаного материала, малые числа Фруда, грядовый и безгрядовый транспорт донных наносов или рифели), для расчета расхода донных наносов целесообразно использовать формулу С. Х. Абальянца (кг/с). м

Номограммы для определения скорости • Примеры расчета смещения мезоформ движения русловых мезоформ по формуле: • за прогнозируемый период Пример 1. Определить смещение побочня за 30 лет в поперечном сечении 15 Прогнозируемые поперечные профили русла

Расчет плановых смещений излучин меандрирующих рек. - величина перемещения береговой линии в поперечнике n - наибольшая скорость перемещения береговой линии на участке , где - коэффициент скорости развития излучины -угол разворота 10 20 30 40 55 70 85 100 125 170 215 240 260 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8 T - период прогнозирования - наибольшая глубина в данном поперечнике - наибольшая глубина на участке излучины 0. 9 1. 0 0. 9 0. 8 0. 7

Перспективы создания методов оценки гидрологических и гидравлических характеристик неизученных рек на основе гидроморфологических зависимостей.

С. И. Рыбкин (1947) ά 1=4, 67; m 1=0. 57; n 1=0. 13; -P 1=0. 07 ά 2=0. 069; m 2=0. 22; n 2=0. 50; -P 2=0. 24 ά 3=3. 10; m 2=0. 21; n 2=0. 37; -P 2=0. 31 Калинин, Белинский (1957)

М. А. Великанов A 1 A 2 X 1 X 2 Великанов 5, 6 0, 29 0, 40 0, 35 Шарашкина 0, 78 0, 49 0, 54 0, 30 Андреев 1, 2 0, 53 0, 51 0, 30 Похсрарян 2, 70 0, 14 0, 42 0, 40 Крошкин 1, 85 0, 62 0, 44 0, 22 Бухин 4, 17 0, 51 0, 42 0, 28 Крошкин 1, 85 0, 62 0, 44 0, 34 ал ск

В. Г. Глушков (1) К. В. Гришанин (2), из (3) получаем (3), отсюда (4) В правой части имеем произведение двух критериев подобия • и При изменении уровня оба отмеченных критерия меняются, а число М сохраняется постоянным в пределах бровок русла, т. е. до выхода воды на пойму. Поэтому число М названо инвариантом числа подобия. Эмпирически определено, что значение инварианта М при вариации уровня воды принимает постоянное значение

• Р. Хэй, К. Торн • B=4. 33 Q 0, 5 Iтип растительности • • • • (6) В=3, 33 Q 0. 5 II тип В=2, 73 Q 0. 5 III тип В=2, 34 Q 0. 5 IV тип Z=6. 31 B Nixon, 1959, для рек Великобритании B=2. 99 Q 0. 5 Simons, Albertson, 1967 B=2. 58 Q 0. 5 Kellerhals, 1967 для рек США, Канады, Швейцарии B=3. 26 Q 0. 5 Сharlton, Brown, Benson, 1978, для рек Англии B=3. 74 Q 0. 45 Bray, 1982, реки Канады B=3. 83 Q 0. 53 D-0. 07 (7) (8) (9) (10) (11) (12) (13) (14) (15)

• В. В. Ромашин (16) (17) (18) Западное Закавказье Исходя из постулата В. М. Лохтина (20) (21) (22) или (19) Для меандрирующих рек и однорукавных русел Для участков рек с пойменной многорукавностью (горной и равнинной) (23) (25) (24) (26)