z C 1 D натуральная величина прямой

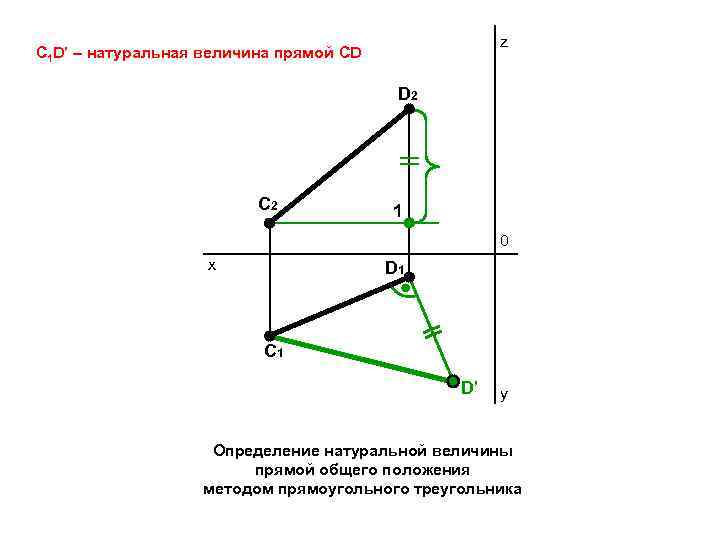z C 1 D’ – натуральная величина прямой CD D 2 C 2 1 0 x D 1 C 1 D’ y Определение натуральной величины прямой общего положения методом прямоугольного треугольника

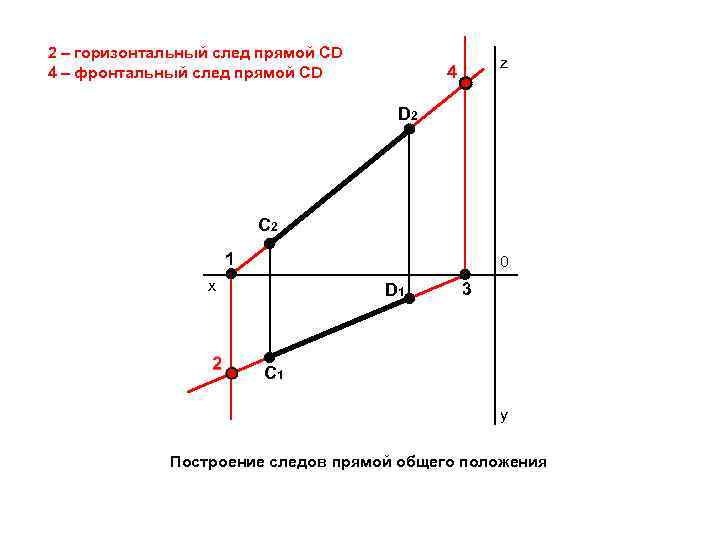2 – горизонтальный след прямой CD 4 – фронтальный след прямой CD z 4 D 2 C 2 1 0 x D 1 3 C 1 y Построение следов прямой общего положения

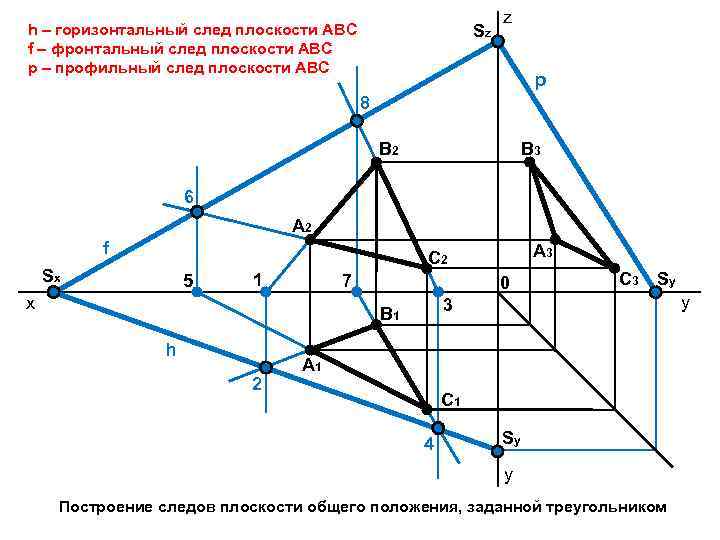h – горизонтальный след плоскости АВC f – фронтальный след плоскости АВC p – профильный след плоскости АВC Sz z p 8 B 3 B 2 6 A 2 f A 3 C 2 Sx 5 1 7 x 0 2 Sy 3 B 1 h C 3 A 1 C 1 4 Sy y Построение следов плоскости общего положения, заданной треугольником y

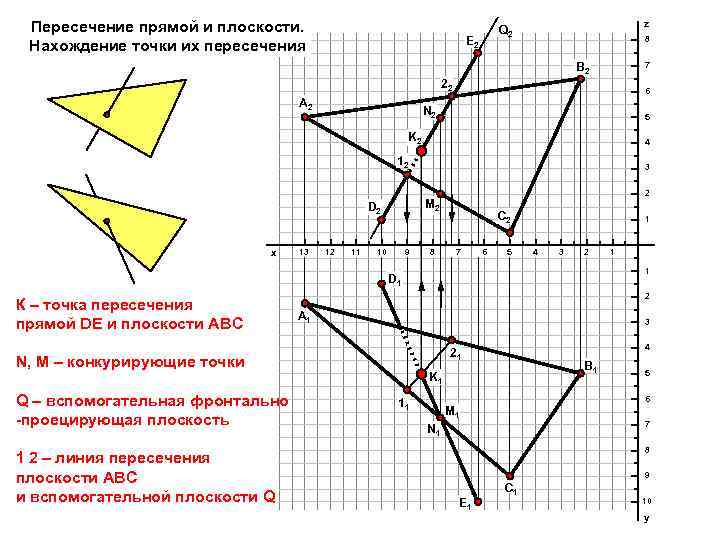Пересечение прямой и плоскости. Нахождение точки их пересечения z Q 2 E 2 8 7 B 2 22 A 2 6 N 2 5 K 2 4 12 13 12 11 2 M 2 D 2 x 3 10 9 8 C 2 7 6 5 1 4 3 2 1 D 1 К – точка пересечения прямой DE и плоскости АВC 2 A 1 3 1 2 – линия пересечения плоскости АВС и вспомогательной плоскости Q 4 21 N, M – конкурирующие точки Q – вспомогательная фронтально -проецирующая плоскость 1 B 1 K 1 5 6 11 M 1 7 N 1 8 9 E 1 C 1 10 y

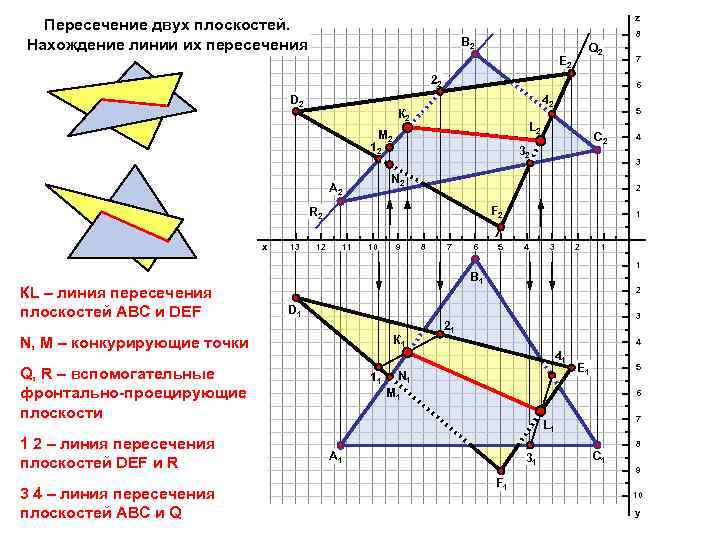z Пересечение двух плоскостей. Нахождение линии их пересечения 8 В 2 Q 2 E 2 22 D 2 6 42 К 2 12 13 12 C 2 32 2 F 2 11 10 9 4 3 N 2 R 2 x 5 L 2 M 2 А 2 7 8 7 6 5 1 4 3 2 1 1 КL – линия пересечения плоскостей АВC и DEF В 1 D 1 N, M – конкурирующие точки К 1 3 4 – линия пересечения плоскостей АВС и Q 3 21 4 41 Q, R – вспомогательные фронтально-проецирующие плоскости 1 2 – линия пересечения плоскостей DEF и R 2 11 N 1 E 1 5 M 1 6 7 L 1 8 А 1 31 F 1 C 1 9 10 y

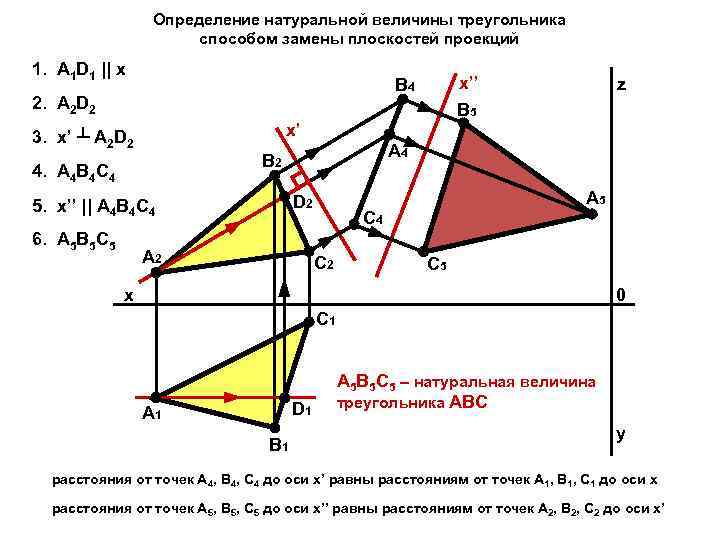Определение натуральной величины треугольника способом замены плоскостей проекций 1. A 1 D 1 || x 2. A 2 D 2 z x’ 3. x’ ┴ A 2 D 2 A 4 B 2 4. A 4 B 4 C 4 D 2 5. x’’ || A 4 B 4 C 4 6. A 5 B 5 C 5 x’’ B 5 B 4 A 2 A 5 C 4 C 2 C 5 x 0 C 1 D 1 A 1 B 1 A 5 B 5 C 5 – натуральная величина треугольника ABC y расстояния от точек A 4, B 4, C 4 до оси x’ равны расстояниям от точек A 1, B 1, C 1 до оси x расстояния от точек A 5, B 5, C 5 до оси x’’ равны расстояниям от точек A 2, B 2, C 2 до оси x’

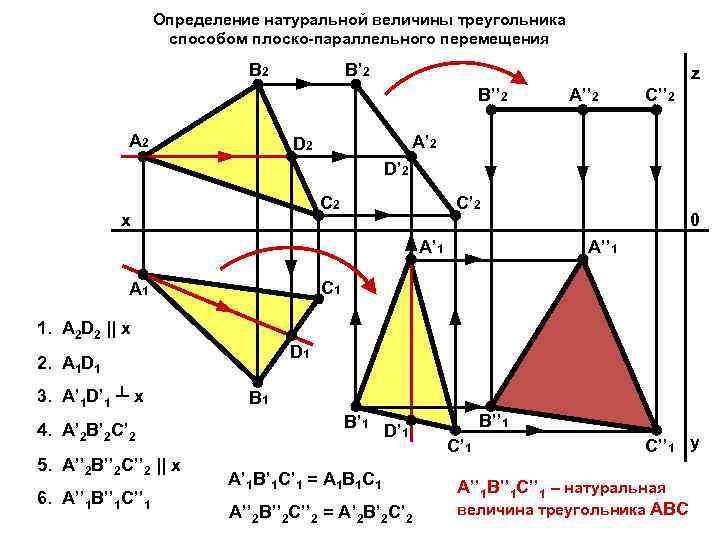Определение натуральной величины треугольника способом плоско-параллельного перемещения B 2 B’ 2 z B’’ 2 A’’ 2 С’’ 2 A’ 2 D’ 2 C 2 x C’ 2 A’ 1 0 A’’ 1 C 1 A 1 1. A 2 D 2 || x D 1 2. A 1 D 1 3. A’ 1 D’ 1 ┴ x 4. A’ 2 B’ 2 C’ 2 5. A’’ 2 B’’ 2 C’’ 2 || x 6. A’’ 1 B’’ 1 C’’ 1 B’ 1 D’ 1 A’ 1 B’ 1 C’ 1 = A 1 B 1 C 1 A’’ 2 B’’ 2 C’’ 2 = A’ 2 B’ 2 C’ 2 B’’ 1 C’’ 1 y A’’ 1 B’’ 1 C’’ 1 – натуральная величина треугольника ABC

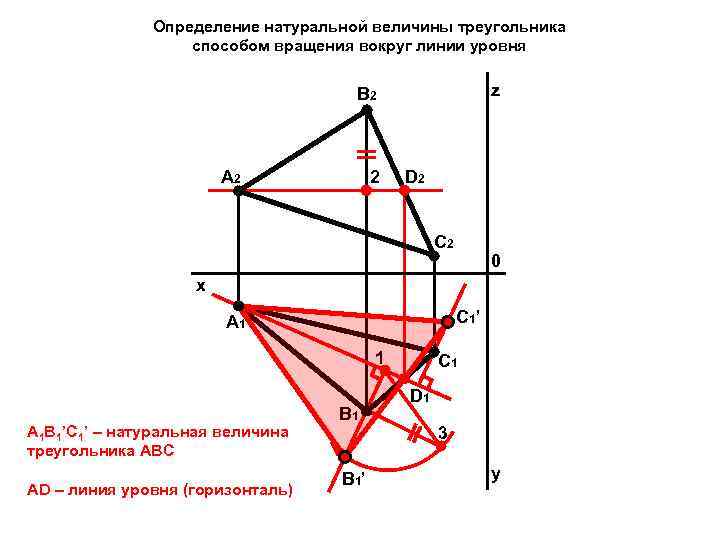Определение натуральной величины треугольника способом вращения вокруг линии уровня z B 2 A 2 2 D 2 C 2 0 x C 1’ A 1 1 А 1 В 1’C 1’ – натуральная величина треугольника АВС AD – линия уровня (горизонталь) B 1’ C 1 D 1 3 y

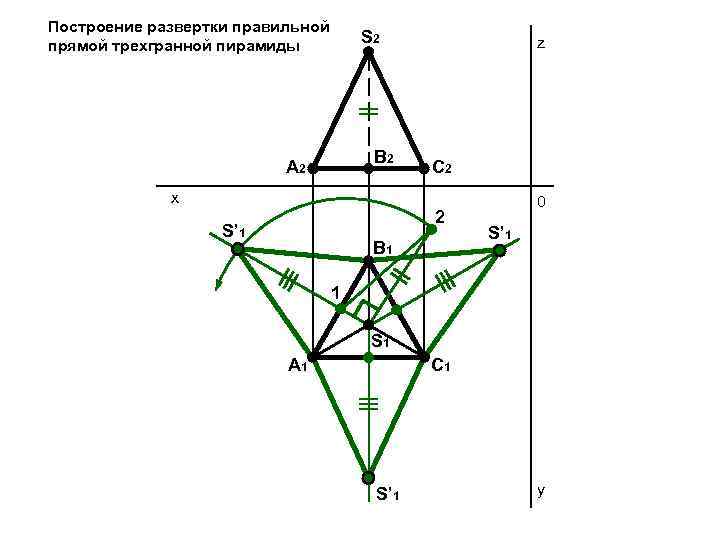Построение развертки правильной прямой трехгранной пирамиды S 2 B 2 A 2 z С 2 x 2 S’ 1 B 1 0 S’ 1 1 S 1 A 1 С 1 S’ 1 y

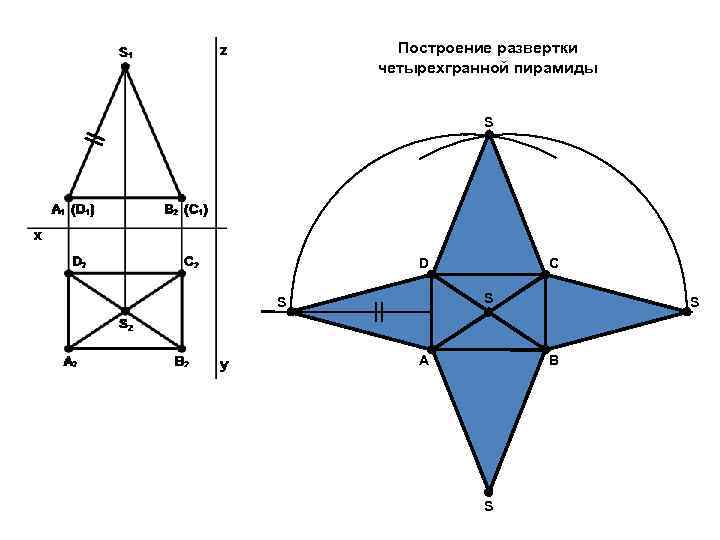Построение развертки четырехгранной пирамиды S D С S S A S B S

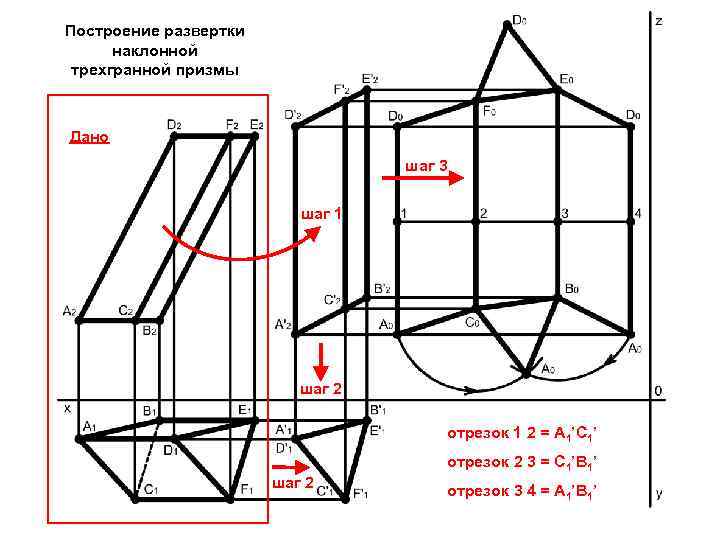Построение развертки наклонной трехгранной призмы Дано шаг 3 шаг 1 шаг 2 отрезок 1 2 = А 1’C 1’ отрезок 2 3 = C 1’B 1’ шаг 2 отрезок 3 4 = A 1’B 1’

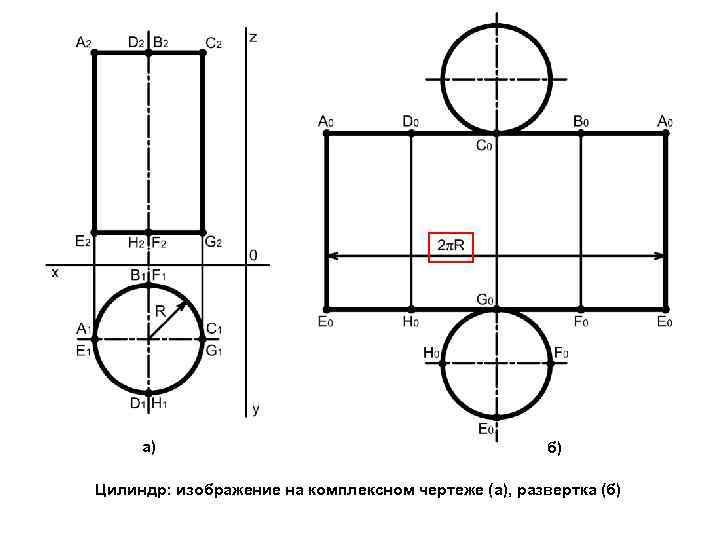а) б) Цилиндр: изображение на комплексном чертеже (а), развертка (б)

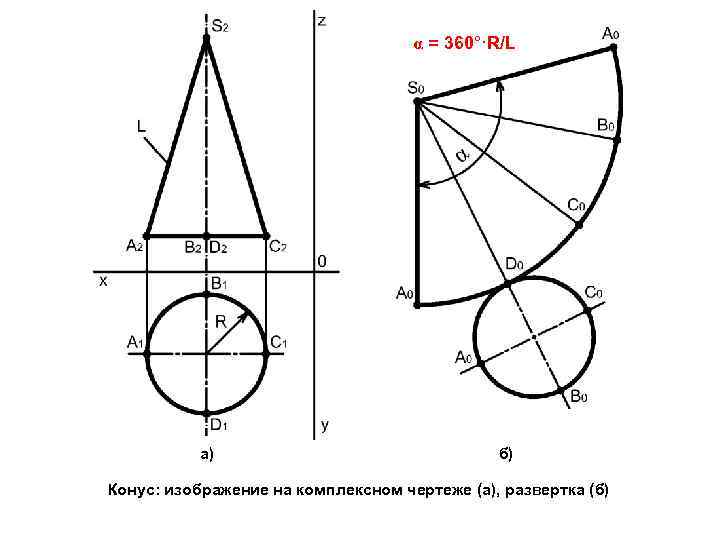α = 360°·R/L а) б) Конус: изображение на комплексном чертеже (а), развертка (б)

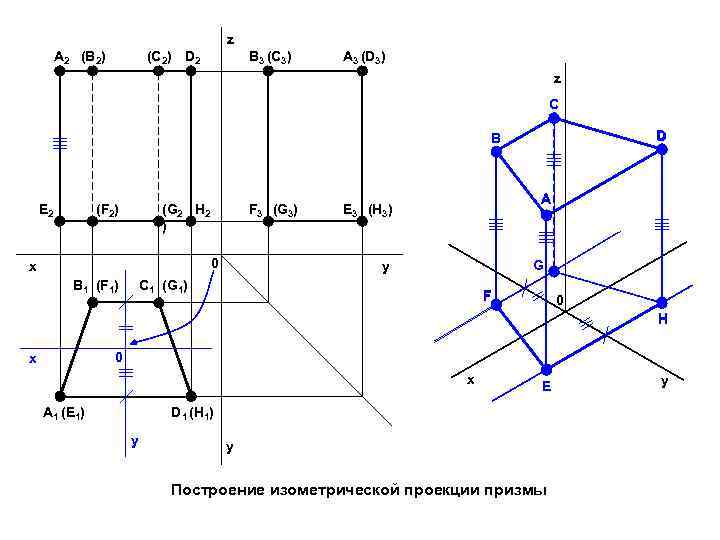z A 2 (B 2) (C 2) D 2 B 3 (С 3) A 3 (D 3) z С D B E 2 (F 2) (G 2 H 2 ) F 3 (G 3) 0 х B 1 (F 1) A E 3 (H 3) G y С 1 (G 1) F 0 H 0 х х A 1 (E 1) E D 1 (H 1) y y Построение изометрической проекции призмы y

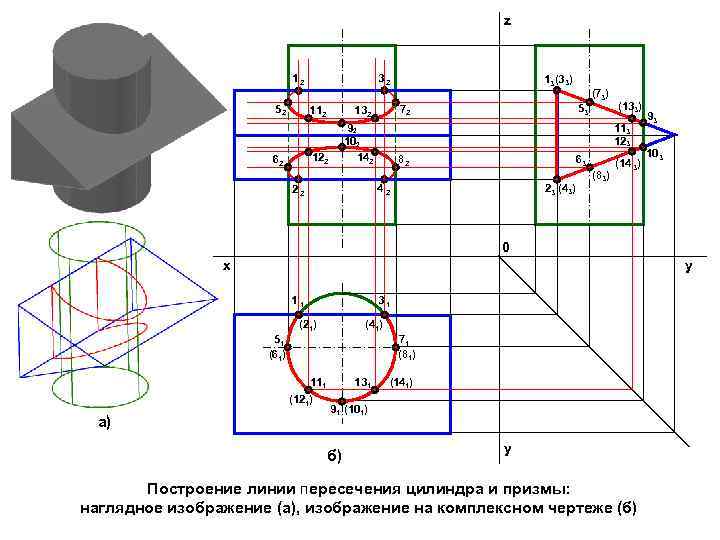z 12 52 32 112 92 102 142 53 (133) 113 123 82 63 23 (43) 42 22 (73) 72 132 122 62 13 (33) (83) (14 3) 93 103 0 x y 11 31 (21) (41) 51 (61) 71 (81) 111 (121) а) 131 (141) 91 (101) б) y Построение линии пересечения цилиндра и призмы: наглядное изображение (а), изображение на комплексном чертеже (б)

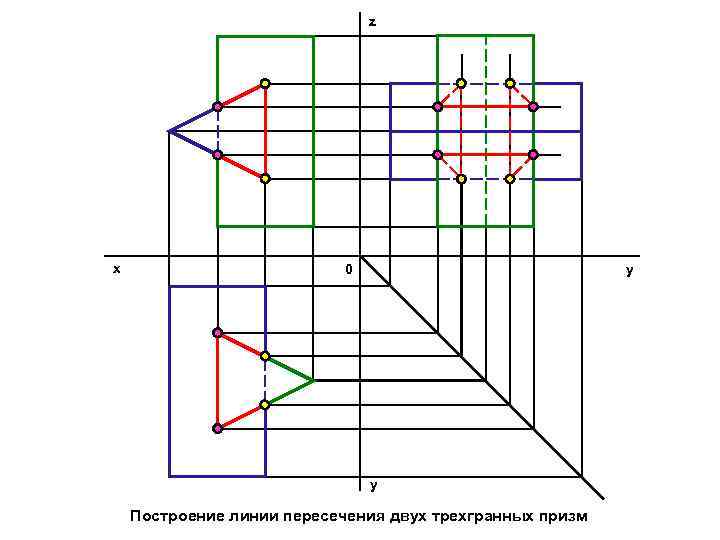z х 0 y y Построение линии пересечения двух трехгранных призм