5ddfb6393816c9870736e0200fd76643.ppt
- Количество слайдов: 20

Южный федеральный университет Институт нанотехнологий, электроники и приборостроения «Поглощение звука звуком: от идеи до воплощения» Гаврилов Александр Максимович д. ф. -м. н. Кафедра физики 1

1. ПАССИВНЫЕ СПОСОБЫ подавления звука: 2 1). - использование отражающих и поглощающих звук материалов, панелей, конструкций и покрытий (авиация, судостроение, автомобили, строительство, машиностроение); 2). - использование резонансных поглотителей (концертные залы); 3). – использование звуковых «ловушек» (в УЗ датчиках). Полное подавление звука — очень непростая задача. Учёными США из лаборатории Орфилд (Миннеаполис) создана «тихая комната» , где удается поглотить 99. 99% внешних звуков. Находясь в «тихой комнате» можно услышать разве что биение собственного сердца. Комнату используют для контроля звуков приборов и устойчивости к стрессам астронавтов NASA.

2. БОРЬБА С ЗВУКООБРАЗОВАНИЕМ: БЕСШУМНОЕ ОРУЖИЕ Давно прошли времена, когда гром выстрелов был неизбежен и необходим для деморализации врага. На смену открытым боевым схваткам приходят специальные операции, где требуется тихое оружие, - без пламени и дыма, не выдающее стрелка. Причины, вызывающие звук при выстреле? 1). - звуки работы механизмов: стук затвора, курка, ударника, частей автоматики. 2). - шум, создаваемый в момент выталкивания из ствола воздуха и пули, пороховыми газами, вырывающимися в зазор между пулей и стволом. 3). - ударная волны от пули, покидающей ствол со сверхзвуковой скоростью. В стволе давление и температура пороховых газов достигают 200 атм. и 1000 С. Вылетая вслед за пулей, газы мгновенно расширяются с оглушительным грохотом. Выстрел намного тише, если: 1). - скорость пули будет дозвуковой, 2). - давление пороховых газов на выходе ствола снизить в 100 раз, 3). - температуру газа снизить более чем в 30 раз. «РУССКИЙ ШЕПОТ» В разработке бесшумных боеприпасов отечественные оружейники намного опередили зарубежных. Идея состоит в том, чтобы после выстрела не выпускать из ствола пороховые газы, наглухо запирать их в замкнутом пространстве. Идея возникла более века назад. Создание в нашей стране патронов с отсечкой газов вызвало на Западе настоящий переполох, а сами комплексы (оружие-патрон) получили название «Русский шепот» . В годы ВОВ на Тульском оружейном заводе инженер Гуревич разработал патрон необыкновенной конструкции. Внутри гильзы, впереди порохового заряда, находился поршень. Пространство между поршнем и пулей заполняла вода. При выстреле пороховые газы толкали поршень, тот давил на воду, а вода - на пулю. Дойдя до конца гильзы, поршень останавливался, упираясь в уступ, и запирал выход газам. Пуля продолжала двигаться под напором воды, выходила из ствола и летела к цели. Шума почти не было, но большое облако брызг выдавало бойца. 3

3. АКТИВНЫЕ СПОСОБЫ: поглощение звука звуком (ПЗЗ) – это уменьшение энергии (амплитуды) волны, называемой сигнальной волной, реализуемый при взаимодействии с другой волной (накачкой) в среде распространения. Механизмы ПЗЗ: 1. ЛИНЕЙНЫЙ механизм ПЗЗ – основан на интерференции 2 -х (или более) волн. Особенности реализации: для 2 -х «взаимодействующих» (интерферирующих) волн – это равенство их частот ( С = Н) и амплитуд (VC = VH), фазы волн отличаются на с - Н = (т. е. противоположны). Амплитуды обеих волн считаем малыми. Недостатки: 1). – сохраняется спектральный состав взаимодействующих волн; 2). – волновая энергия перераспределяется в пространстве без преобразования акустической энергии в тепловую энергию, т. е. амплитуда сигнальной волны снижается только в ограниченной области пространства. 2. НЕЛИНЕЙНЫЙ механизм ПЗЗ – основан на нелинейном взаимодействии 2 -х (или более) волн в среде распространения, используя нелинейные свойства среды. Особенности реализации: амплитуды волн сигнала и накачки соотносятся VC << VH; волна накачки имеет конечную амплитуду (достаточную для осуществления нелинейных процессов); частоты сигнала С и накачки Н могут быть связаны разными соотношениями. Преимущества: 1). - преобразуется частотный спектр (появляются новые частоты); 2). - уменьшается амплитуда сигнальной волны за счет передачи ее энергии в новые Фурье-компоненты; 3). – необратимое преобразование волновой энергии сигнала в тепловую энергию за счет усиленной диссипации ВЧ гармоник. 4
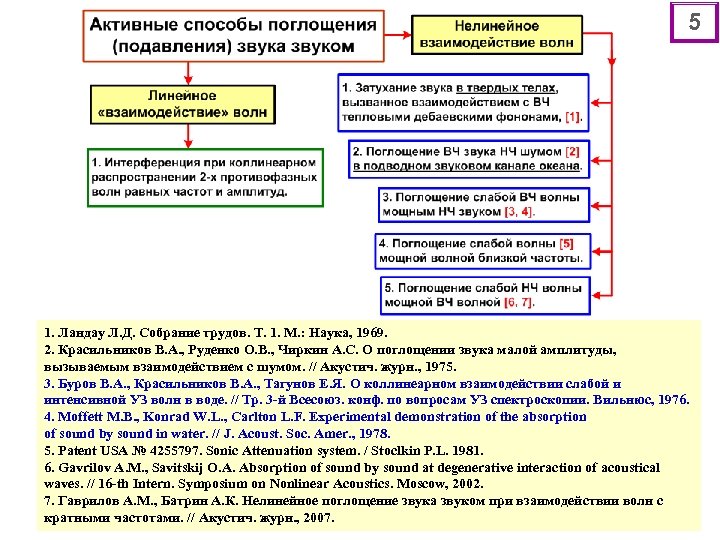
5 1. Ландау Л. Д. Собрание трудов. Т. 1. М. : Наука, 1969. 2. Красильников В. А. , Руденко О. В. , Чиркин А. С. О поглощении звука малой амплитуды, вызываемым взаимодействием с шумом. // Акустич. журн. , 1975. 3. Буров В. А. , Красильников В. А. , Тагунов Е. Я. О коллинеарном взаимодействии слабой и интенсивной УЗ волн в воде. // Тр. 3 -й Всесоюз. конф. по вопросам УЗ спектроскопии. Вильнюс, 1976. 4. Moffett M. B. , Konrad W. L. , Carlton L. F. Experimental demonstration of the absorption of sound by sound in water. // J. Acoust. Soc. Amer. , 1978. 5. Patent USA № 4255797. Sonic Attenuation system. / Stoclkin P. L. 1981. 6. Gavrilov A. M. , Savitskij O. A. Absorption of sound by sound at degenerative interaction of acoustical waves. // 16 -th Intern. Symposium on Nonlinear Acoustics. Moscow, 2002. 7. Гаврилов А. М. , Батрин А. К. Нелинейное поглощение звука звуком при взаимодействии волн с кратными частотами. // Акустич. журн. , 2007.

Нелинейное взаимодействие – как базовый механизм поглощения звука В твердых телах [см. Л. 1, Ландау Л. Д. ] : - именно нелинейный механизм отбора энергии из звуковой волны положен в основу расчета коэффициента поглощения звука. Волна взаимодействует в процессе распространения с ВЧ тепловыми дебаевскими фононами. В жидкостях и газах [см. Л. 2, Красильников В. А. и др. ]: - поглощение звука за счет вязкости и теплопроводности, описываемое линейными членами уравнений гидродинамики и теплопроводности, можно считать следствием взаимодействия акустической волны с внешним шумом. Поглощение сводится к микроскопическим нелинейным процессам перекачки энергии волны в поступательные и внутренние степени свободы молекул. Особенность протекания нелинейных волновых процессов в АКУСТИКЕ : 1). - полное отсутствие (или очень слабое проявление) частотной дисперсии фазовой скорости, что обеспечивает фазовый синхронизм распространения гармонических волн разных частот; 2). - благодаря фазовому синхронизму исходных (первичных) и вторичных (появились в процессе взаимодействия) волн происходит эффективная перекачка энергии из первичных волн во вторичные; 3). – накопительный характер нелинейных процессов сопровождается образованием «квазистационарных» ударных участков волнового профиля, где энергия волны быстро преобразуется в тепловую через вязкость среды; 4). – невозможность спектрального описания процесса из-за бесконечного числа Фурьекомпонент, что предполагает анализ изменений временного профиля волны. 6

Исходные уравнения нелинейной акустики квадратично-нелинейных сред без дисперсии 1. Уравнение простых волн: плоские волны, идеальная среда (уравнение Римана) 7 Формализация задачи взаимодействия 2 -х гармонических волн с произвольными амплитуднофазовыми и частотными соотношениями Случай № 1: взаимодействие двух гармонических волн с сильно различающимися частотами: w 1/w 2 >> 1, w 1/w 2 << 1; 2. Уравнение Бюргерса: одномерные волны, диссипативная среда Случай № 2: взаимодействие двух гармонических волн с близкими частотами: w 1/w 2 1. 3. Уравнение Хохлова-Заболотской-Кузнецова (ХЗК): дифрагирующие пучки, диссипативная среда Безразмерные переменные и параметры: Re – акустическое число Рейнольдса N – число Хохлова 1. w 1/w 2 >> 1; w 1/w 2 << 1; 2. w 1/w 2 1; 1. w 2 =Nw 1 волны с кратными частотами (N = 2, 3, 4, …); 2. w 1 = nw; w 2 = mw волны с некратным целочисленным соотношением частот (n, m = 1, 2, 3, …)
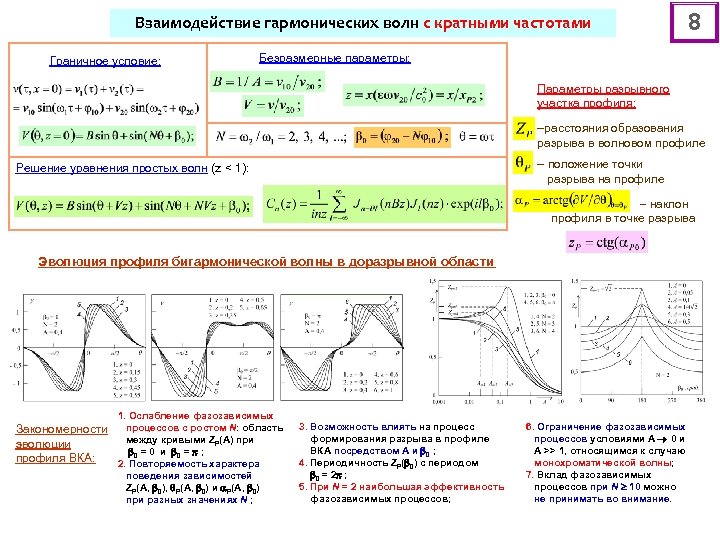
Взаимодействие гармонических волн с кратными частотами Граничное условие: 8 Безразмерные параметры: Параметры разрывного участка профиля: расстояния образования разрыва в волновом профиле положение точки разрыва на профиле Решение уравнения простых волн (z < 1): наклон профиля в точке разрыва Эволюция профиля бигармонической волны в доразрывной области Закономерности эволюции профиля ВКА: 1. Ослабление фазозависимых процессов с ростом N: область между кривыми ZP(A) при 0 = 0 и 0 = ; 2. Повторяемость характера поведения зависимостей ZP(A, 0), P(A, 0) и P(A, 0) при разных значениях N ; 3. Возможность влиять на процесс формирования разрыва в профиле ВКА посредством A и 0 ; 4. Периодичность ZP( 0) с периодом 0 = 2 ; 5. При N = 2 наибольшая эффективность фазозависимых процессов; 6. Ограничение фазозависимых процессов условиями A 0 и A >> 1, относящимся к случаю монохроматической волны; 7. Вклад фазозависимых процессов при N 10 можно не принимать во внимание.
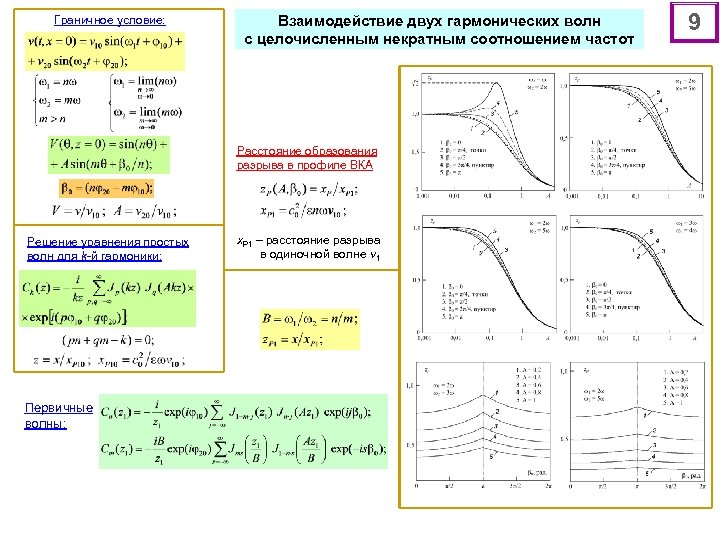
Граничное условие: Взаимодействие двух гармонических волн с целочисленным некратным соотношением частот Расстояние образования разрыва в профиле ВКА Решение уравнения простых волн для k-й гармоники: Первичные волны: x. P 1 – расстояние разрыва в одиночной волне v 1 9
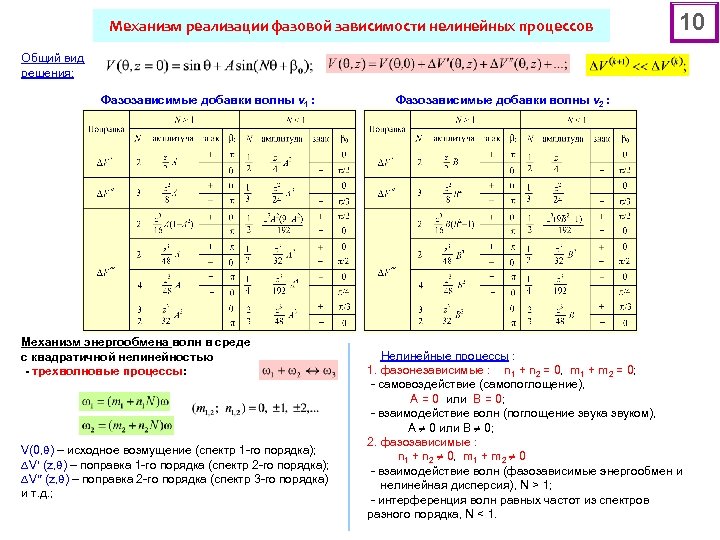
Механизм реализации фазовой зависимости нелинейных процессов 10 Общий вид решения: Фазозависимые добавки волны v 1 : Механизм энергообмена волн в среде с квадратичной нелинейностью - трехволновые процессы: V(0, ) – исходное возмущение (спектр 1 -го порядка); V (z, ) – поправка 1 -го порядка (спектр 2 -го порядка); V (z, ) – поправка 2 -го порядка (спектр 3 -го порядка) и т. д. ; Фазозависимые добавки волны v 2 : Нелинейные процессы : 1. фазонезависимые : n 1 + n 2 = 0, m 1 + m 2 = 0; - самовоздействие (самопоглощение), А = 0 или В = 0; - взаимодействие волн (поглощение звука звуком), А 0 или В 0; 2. фазозависимые : n 1 + n 2 0, m 1 + m 2 0 - взаимодействие волн (фазозависимые энергообмен и нелинейная дисперсия), N > 1; - интерференция волн равных частот из спектров разного порядка, N < 1.
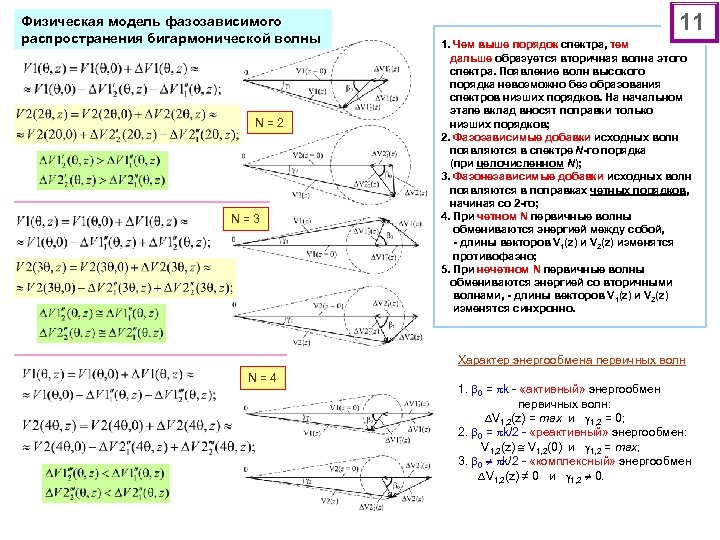
Физическая модель фазозависимого распространения бигармонической волны N = 2 N = 3 N = 4 11 1. Чем выше порядок спектра, тем дальше образуется вторичная волна этого спектра. Появление волн высокого порядка невозможно без образования спектров низших порядков. На начальном этапе вклад вносят поправки только низших порядков; 2. Фазозависимые добавки исходных волн появляются в спектре N-го порядка (при целочисленном N); 3. Фазонезависимые добавки исходных волн появляются в поправках четных порядков, начиная со 2 -го; 4. При четном N первичные волны обмениваются энергией между собой, - длины векторов V 1(z) и V 2(z) изменятся противофазно; 5. При нечетном N первичные волны обмениваются энергией со вторичными волнами, - длины векторов V 1(z) и V 2(z) изменятся синхронно. Характер энергообмена первичных волн 1. 0 = k - «активный» энергообмен первичных волн: V 1, 2(z) = max и 1, 2 = 0; 2. 0 = k/2 - «реактивный» энергообмен: V 1, 2(z) V 1, 2(0) и 1, 2 = max; 3. 0 k/2 - «комплексный» энергообмен V 1, 2(z) ≠ 0 и 1, 2 0.
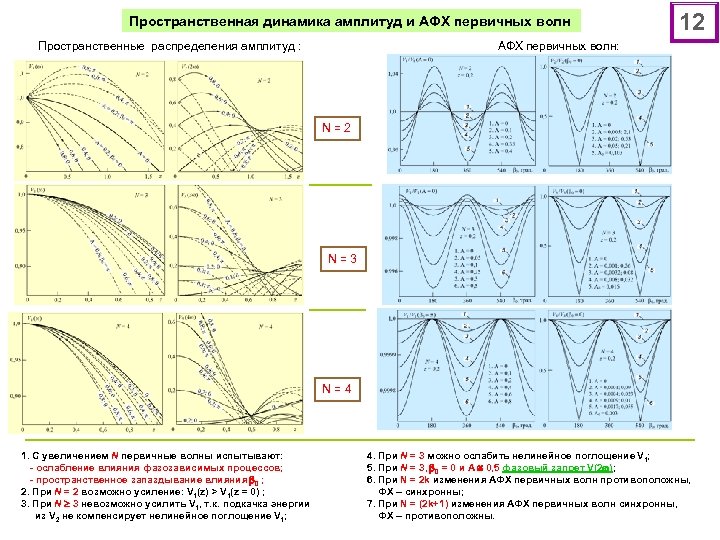
Пространственная динамика амплитуд и АФХ первичных волн Пространственные распределения амплитуд : 12 АФХ первичных волн: N = 2 N = 3 N = 4 1. С увеличением N первичные волны испытывают: - ослабление влияния фазозависимых процессов; - пространственное запаздывание влияния 0 ; 2. При N = 2 возможно усиление: V 1(z) > V 1(z = 0) ; 3. При N 3 невозможно усилить V 1, т. к. подкачка энергии из V 2 не компенсирует нелинейное поглощение V 1; 4. При N = 3 можно ослабить нелинейное поглощение V 1; 5. При N = 3, 0 = 0 и А 0, 5 фазовый запрет V(2 ); 6. При N = 2 k изменения АФХ первичных волн противоположны, ФХ – синхронны; 7. При N = (2 k+1) изменения АФХ первичных волн синхронны, ФХ – противоположны.
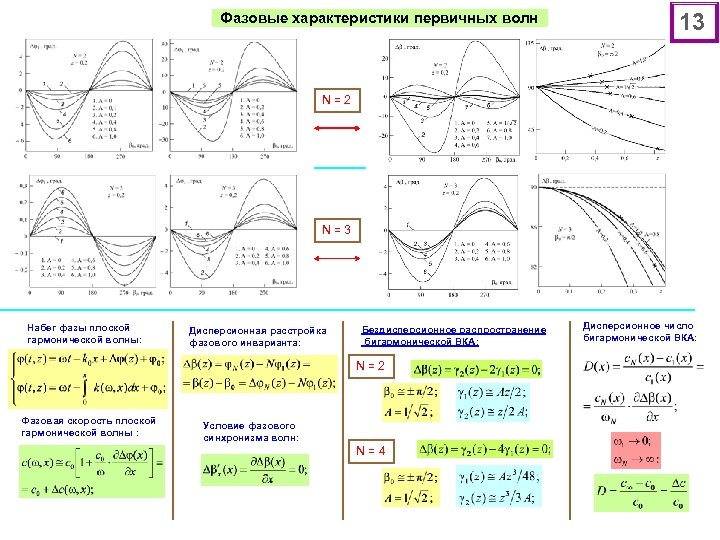
Фазовые характеристики первичных волн 13 N = 2 N = 3 Набег фазы плоской гармонической волны: Дисперсионная расстройка фазового инварианта: Бездисперсионное распространение бигармонической ВКА: N = 2 Фазовая скорость плоской гармонической волны : Условие фазового синхронизма волн: N = 4 Дисперсионное число бигармонической ВКА:
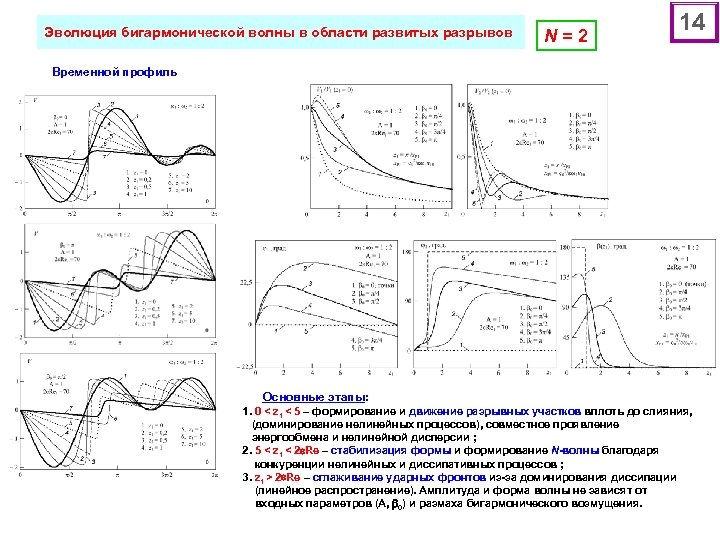
Эволюция бигармонической волны в области развитых разрывов N=2 14 Временной профиль Основные этапы: 1. 0 < z 1 < 5 – формирование и движение разрывных участков вплоть до слияния, (доминирование нелинейных процессов), совместное проявление энергообмена и нелинейной дисперсии ; 2. 5 < z 1 < 2 Re – стабилизация формы и формирование N-волны благодаря конкуренции нелинейных и диссипативных процессов ; 3. z 1 > 2 Re – сглаживание ударных фронтов из-за доминирования диссипации (линейное распространение). Амплитуда и форма волны не зависят от входных параметров (A, 0) и размаха бигармонического возмущения.
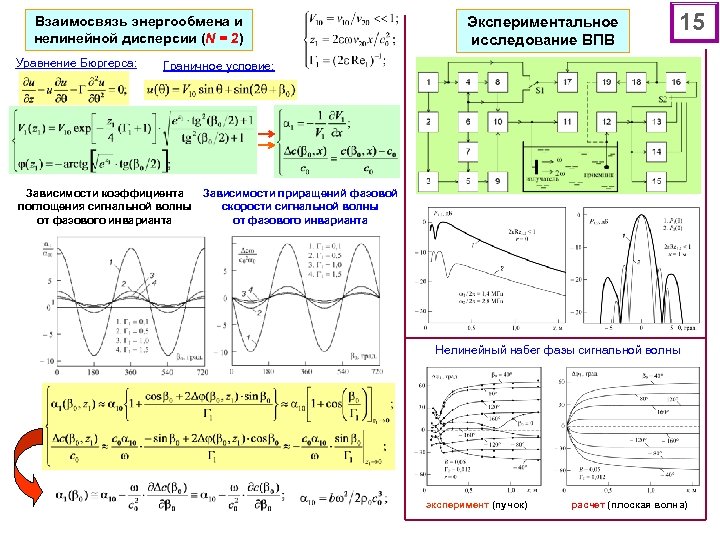
Взаимосвязь энергообмена и нелинейной дисперсии (N = 2) Уравнение Бюргерса: Экспериментальное исследование ВПВ 15 Граничное условие: Зависимости коэффициента поглощения сигнальной волны от фазового инварианта Зависимости приращений фазовой скорости сигнальной волны от фазового инварианта Нелинейный набег фазы сигнальной волны эксперимент (пучок) расчет (плоская волна)

Поглощение звука звуком при взаимодействии 2 -х гармонических волн с кратными частотами Исходное возмущение (граничное условие): 16 Условия проявления фазозависимого поглощения сигнала волной накачки: 0 = 0, N = 2 n 0 = , N = (2 n – 1) n = 1, 2, 3, … Общее решение (z 1): Коэффициент нелинейного поглощения сигнала при N = 2, 3, … N = 2: N 3: Наблюдаемые закономерности: 1. - фазонезависимое поглощение проявляется в спектре 2 -го порядка независимо от величины N; 2. - фазозависимое поглощение появляется в спектре N-го порядка; 3. - при N ≥ 3 его влияние пренебрежимо.
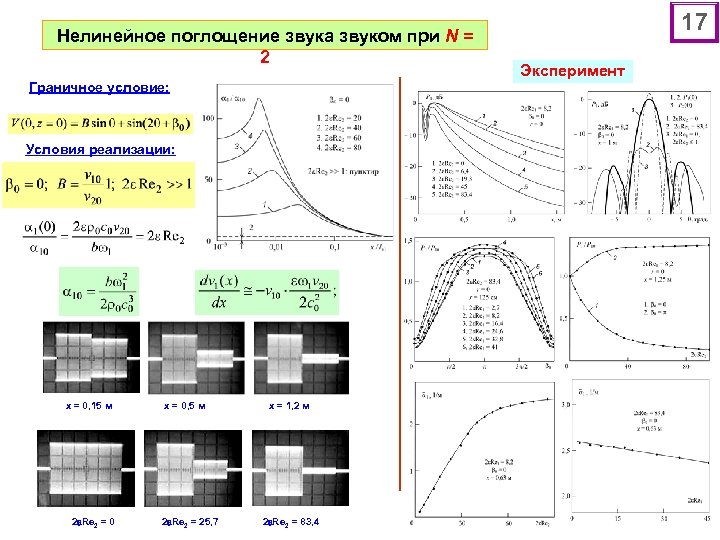
Нелинейное поглощение звука звуком при N = 2 Граничное условие: Условия реализации: х = 0, 15 м 2 Re 2 = 0 х = 0, 5 м 2 Re 2 = 25, 7 х = 1, 2 м 2 Re 2 = 83, 4 17 Эксперимент
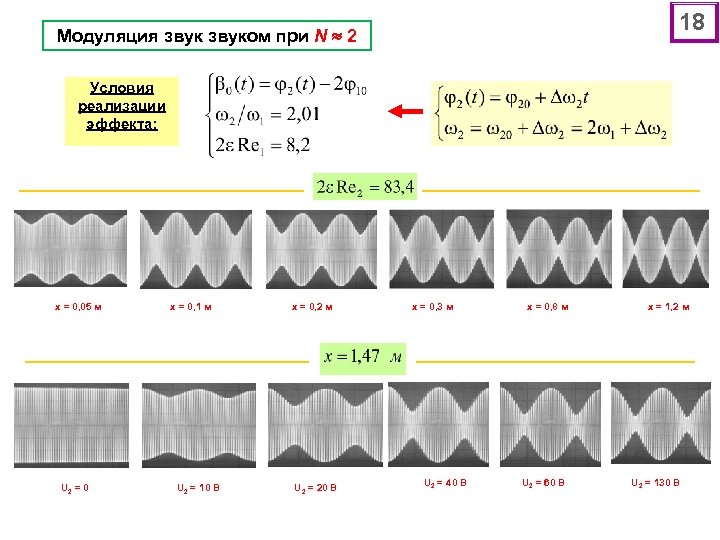
18 Модуляция звуком при N 2 Условия реализации эффекта: х = 0, 05 м U 2 = 0 х = 0, 1 м U 2 = 10 B х = 0, 2 м U 2 = 20 B х = 0, 3 м U 2 = 40 B х = 0, 8 м U 2 = 60 B х = 1, 2 м U 2 = 130 B
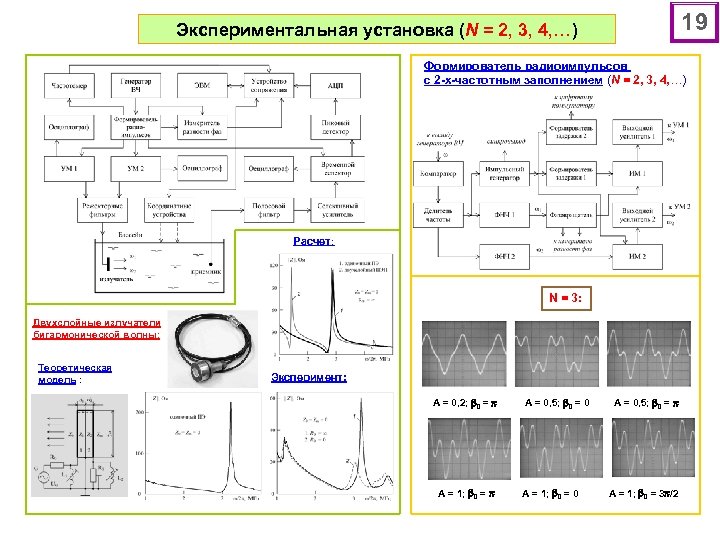
19 Экспериментальная установка (N = 2, 3, 4, …) Формирователь радиоимпульсов с 2 -х-частотным заполнением (N = 2, 3, 4, …) Расчет: N = 3: Двухслойные излучатели бигармонической волны: Теоретическая модель : Эксперимент: A = 0, 2; 0 = A = 1; 0 = A = 0, 5; 0 = 0 A = 1; 0 = 0 A = 0, 5; 0 = A = 1; 0 = 3 /2

Экспериментальная лабораторная установка 20
5ddfb6393816c9870736e0200fd76643.ppt