Скачать презентацию Южно-Уральский государственный университет Управление портфелем активов Тема 1 Скачать презентацию Южно-Уральский государственный университет Управление портфелем активов Тема 1

UPA_Tema1_2.ppt

  • Количество слайдов: 81

Южно-Уральский государственный университет Управление портфелем активов Тема 1. Введение в курс Моцаренко Наталья Васильевна Южно-Уральский государственный университет Управление портфелем активов Тема 1. Введение в курс Моцаренко Наталья Васильевна доцент кафедры «Экономическая теория и мировая экономика» Челябинск 2010

Управление портфелем активов Тема 1. Введение в курс 1. Портфель активов и его инвестиционные Управление портфелем активов Тема 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики. 2. Традиционный и современный подход к управлению портфелем Слайд # 2 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Портфельное инвестирование, то есть вложение средств в набор различных активов – это широко распространенное явление в мировой и российской практике финансовых инвестиций. К портфельным инвестициям прибегают, прежде институциональные инвесторы (паевые инвестиционные компании, коммерческие банки и пр. ). всего, фонды, Частные инвесторы участвуют в портфельных инвестициях самостоятельно, с помощью консалтинговых компаний, через доверительное управление, а также посредством приобретения паев инвестиционных фондов. Основные признаки, по которым могут различаться финансовых активов представлены на слайде 4. Слайд # 3 Челябинск 2010 портфели Кафедра ЭТи. МЭ

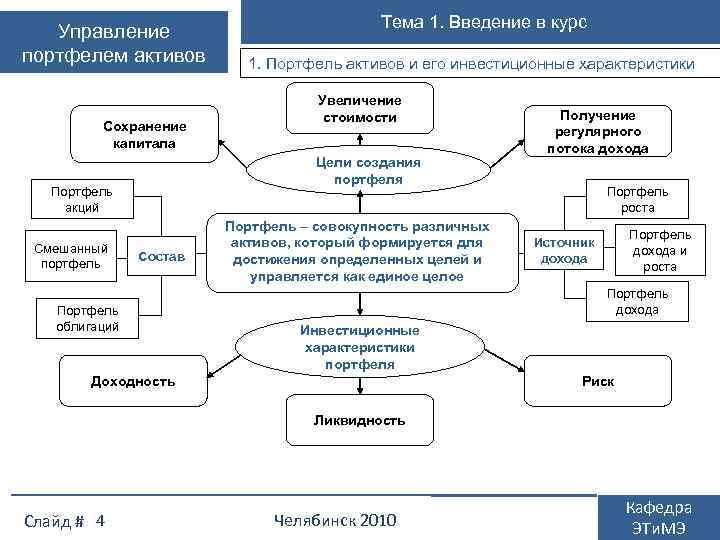Управление портфелем активов Сохранение капитала 1. Портфель активов и его инвестиционные характеристики Увеличение стоимости Управление портфелем активов Сохранение капитала 1. Портфель активов и его инвестиционные характеристики Увеличение стоимости Цели создания портфеля Портфель акций Смешанный портфель Тема 1. Введение в курс Состав Портфель облигаций Портфель – совокупность различных активов, который формируется для достижения определенных целей и управляется как единое целое Получение регулярного потока дохода Портфель роста Портфель дохода и роста Источник дохода Портфель дохода Инвестиционные характеристики портфеля Доходность Риск Ликвидность Слайд # 4 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Основные инвестиционные характеристики портфеля: 1. Доходность – способность портфеля генерировать поток доходов в течение периода инвестирования. Измеряется, как и для отдельного актива, отношением прироста стоимости за период к начальной стоимости портфеля Доходность портфеля может быть обусловлена: • изменением рыночных цен входящих в него активов; • промежуточными доходами, которые приносят финансовые активы. Слайд # 5 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики 2. Ликвидность – возможность трансформировать портфель в целом или какую-либо его часть в денежные средства (продать) быстро, без существенных издержек и потерь в стоимости. 3. Риск – вероятность потерь стоимости портфеля или снижения доходности по сравнению с ожидаемой в результате непредвиденного изменения рыночных цен финансовых активов, входящих в портфель. В совокупности указанные инвестиционное качество портфеля. характеристики определяют Ликвидность обычно рассматривается как ограничение при формировании портфеля, необходимое для эффективного управления портфелем. Соотношение доходности и риска является объектом оптимизации портфеля Слайд # 6 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Работа с финансовым портфелем напоминает работу с отдельными финансовыми инструментами. так как портфель рассматривается как одно целое и также характеризуется доходностью и риском. Принципиальное отличие: • характеристики отдельных финансовых инструментов определяются свойствами их эмитентов и состоянием рынка; • характеристики портфеля. зависят также от решений инвестора, который может их изменять, варьируя составом портфеля. Слайд # 7 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Управление портфелем активов 1. Введение в курс 1. Портфель активов и его инвестиционные характеристики Основная задача портфельного инвестирования: улучшить условия инвестирования, придав совокупности активов такие характеристики, которые недостижимы с позиций отдельно взятых активов и возможны только при их комбинации. Преимущества портфельного инвестирования: • позволяет улучшить соотношение доходность / риск по сравнению с инвестированием в отдельный активы; • позволяет оптимизировать структуру портфеля с точки зрения предпочтений инвестора относительно доходности и его отношения к риску. При инвестировании в портфель создается новое инвестиционное качество. Слайд # 8 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 2. Традиционный и современный подход к управлению Управление портфелем активов 1. Введение в курс 2. Традиционный и современный подход к управлению портфелем Традиционный подход • основан на правилах, выработанных в результате практического опыта; • предполагает создание «сбалансированного» портфеля, включающего активы разных предприятий, отраслей и сфер деятельности; • ориентирован на вложения в ценные бумаги известных, хорошо зарекомендовавших себя компаний; • главное при формировании портфеля – инвестиционные качества отдельных ценных бумаг; • оценивается в основном доходность портфеля, риск в явном виде не определяется, но предполагается, что вложение средств в различные активы снижает уровень риска. Слайд # 9 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Введение в курс 2. Традиционный и современный подход к управлению Управление портфелем активов 1. Введение в курс 2. Традиционный и современный подход к управлению портфелем Современный подход • основан на теории выбора портфеля; • главное – анализ «поведения» портфеля в целом; • отдельные ценные бумаги оцениваются с точки зрения вклада в доходность и риск портфеля; • используется математический инструментарий оптимизации портфеля по критерию доходность – риск; Основоположник теории портфеля Гарри Марковиц. 1952 г. статья им опубликована статья «Выбор портфеля» , в которой впервые была предложена математическая модель оптимизации портфеля и рассмотрены методы его формирования. Развитие теории портфеля : У. Шарп, Дж. Тобин, Дж. Линтнером и др. Важность разработки теории портфеля для развития современной экономики и финансов подчеркивает Нобелевская премия по экономике, которой были удостоены Гарри Марковиц, Джеймс Тобин и Вильям Шарп в первую очередь за работы этой области. Слайд # 10 Челябинск 2010 Кафедра ЭТи. МЭ

Южно-Уральский государственный университет Управление портфелем активов Тема 2. Доходность и риск портфеля активов Моцаренко Южно-Уральский государственный университет Управление портфелем активов Тема 2. Доходность и риск портфеля активов Моцаренко Наталья Васильевна доцент кафедры «Экономическая теория и мировая экономика» Челябинск 2010

Управление портфелем активов Тема 2. Доходность и риск портфеля активов 1. Доходность и риск Управление портфелем активов Тема 2. Доходность и риск портфеля активов 1. Доходность и риск финансовых активов (см. курс «Управление финансовыми рисками» ) 2. Измерение доходности и риска портфеля 3. Диверсификация и риск портфеля. Эффект диверсификации. Слайд # 12 Челябинск 2010 Кафедра ЭТи. МЭ

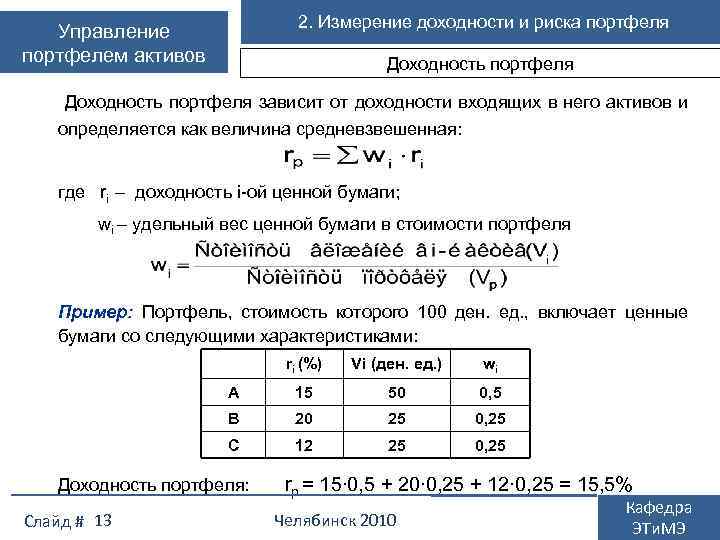2. Измерение доходности и риска портфеля Управление портфелем активов Доходность портфеля зависит от доходности 2. Измерение доходности и риска портфеля Управление портфелем активов Доходность портфеля зависит от доходности входящих в него активов и определяется как величина средневзвешенная: где ri – доходность i-ой ценной бумаги; wi – удельный вес ценной бумаги в стоимости портфеля Пример: Портфель, стоимость которого 100 ден. ед. , включает ценные бумаги со следующими характеристиками: ri (%) Vi (ден. ед. ) wi А 15 50 0, 5 В 20 25 0, 25 С 12 25 0, 25 Доходность портфеля: Слайд # 13 rp = 15∙ 0, 5 + 20∙ 0, 25 + 12∙ 0, 25 = 15, 5% Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Наиболее распространенными показателями Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Наиболее распространенными показателями риска портфеля, также как и для отдельных активов, являются дисперсия и стандартное отклонения доходностей. Риск портфеля зависит от риска входящих в него ценных бумаг, но как правило, оказывается меньше средневзвешенного риска активов, т. е. Это объясняется тем, что доходность разных ценных бумаг может меняться в определенные моменты времени в разных направлениях, взаимно компенсируя колебания доходности. Поэтому риск портфеля зависит от степени согласованности в изменении доходности активов, включенных в портфель. Слайд # 14 Челябинск 2010 Кафедра ЭТи. МЭ

2. Измерение доходности и риска портфеля Управление портфелем активов Риск портфеля Показателями степени согласованности 2. Измерение доходности и риска портфеля Управление портфелем активов Риск портфеля Показателями степени согласованности в изменении доходности активов являются: ковариация доходностей ( covij ); коэффициент корреляции ( ρij ). Ковариация доходностей ценных бумаг А и В определяется по формулам: При вероятностном подходе: При статистическом подходе: Чем больше ковариация, тем более согласованно колеблются доходности двух ценных бумаг. Положительное значение ковариации означает. что доходности активов чаще меняются в одном направлении и реже – в разных. Отрицательное значение ковариации свидетельствует об обратном. Слайд # 15 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Коэффициент корреляции доходностей Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Коэффициент корреляции доходностей двух ценных бумаг определяется на основе показателя ковариации по формуле: Значения коэффициента корреляции могут находиться в пределах: Если ρ = +1, то имеет место полная согласованность в колебаниях доходностей активов, которые всегда изменяются в одном направлении. При ρ = -1 также имеет место полная согласованность, но доходности активов всегда меняются в разных направлениях. Во всех других случаях существует неполная согласованность в изменении доходности, при ρ = 0 какая-либо связь в изменении доходности двух активов отсутствует. Слайд # 16 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Для определения риска Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Для определения риска портфеля необходимы следующие данные: • удельные веса ценных бумаг в стоимости портфеля (wi); • дисперсия (вариация) доходности каждого актива (σi 2); • ковариации (корреляция) доходностей каждого актива со всеми активами в портфеле (covij; ρij) Для расчета риска портфеля составляется ковариационная (корреляционная) матрица, где записываются дисперсии и ковариации всех активов, входящих в портфель. Например, при формировании портфеля из двух активов матрица будет содержать 4 элемента (две дисперсии и две ковариации), а при создании в портфеля из 20 ценных бумаг должны быть рассчитаны 400 значений (20 дисперсий и 380 ковариации). Слайд # 17 Челябинск 2010 Кафедра ЭТи. МЭ

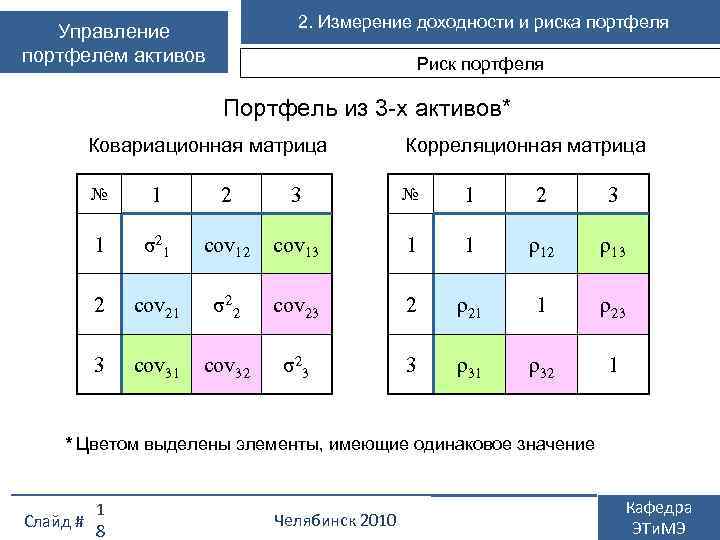2. Измерение доходности и риска портфеля Управление портфелем активов Риск портфеля Портфель из 3 2. Измерение доходности и риска портфеля Управление портфелем активов Риск портфеля Портфель из 3 -х активов* Ковариационная матрица Корреляционная матрица № 1 2 3 1 σ21 cov 12 cov 13 1 1 ρ12 ρ13 2 cov 21 σ22 cov 23 2 ρ21 1 ρ23 3 cov 31 cov 32 σ23 3 ρ31 ρ32 1 * Цветом выделены элементы, имеющие одинаковое значение Слайд # 1 8 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля из «n» активов Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля из «n» активов рассчитывается по формуле: При включении в портфель 2 -х активов формула стандартного отклонения портфеля имеет вид**: **Ковариация может быть выражена через коэффициент корреляции: Слайд # 19 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Формула оценки риска Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля Формула оценки риска портфеля из 2 -х активов с использованием коэффициента корреляции позволяет показать влияние степени согласованности в движении доходностей активов на риска портфеля. Если ρ=+1, риск портфеля окажется средневзвешенной величиной риска активов, снижения уровня риска не произойдет: При ρ = – 1 появляется возможность, подобрав удельные веса активов, создать из них безрисковый портфель. Определение удельного веса активов: Слайд # 20 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля На реальном рынке Управление портфелем активов 2. Измерение доходности и риска портфеля Риск портфеля На реальном рынке коэффициенты корреляции, как правило находятся между крайними значениями. Поэтому риск портфеля оказывается меньше средневзвешенного риска входящих в него активов. Неполная корреляция доходностей различных ценных бумаг порождает эффект диверсификации. Диверсификация – распределение общей суммы вложенных средств между различными инвестиционными активами. Слайд # 21 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Эффект диверсификации состоит в том, что Управление портфелем активов 3. Диверсификация и риск портфеля Эффект диверсификации состоит в том, что она позволяет достичь снижения риска, не уменьшая в той же мере доходности инвестиций. Иначе: эффект диверсификации выражается в улучшении соотношения доходности и риска по сравнению с вложением средств в отдельные активы. Но диверсификация, как правило, не может полностью устранить риск. Это обусловлено тем, что ценные бумаги подвержены двум видам риска: • рыночному (систематическому) риску; • специфическому (собственному) риску. Слайд # 22 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Структура риска рыночных ценных бумаг Рыночный Управление портфелем активов 3. Диверсификация и риск портфеля Структура риска рыночных ценных бумаг Рыночный риск имеет макроэкономическую природу, он обусловлен колебаниями экономической конъюнктуры в целом и колебаниями доходности рынка ценных бумаг. Данному виду риска подвержены в той или иной мере все финансовые активы. Рыночный риск не устраняется, а лишь усредняется при диверсификации портфеля. Рыночный риск – это недиверсифицируемый риск. Специфический риск имеет в основном микроэкономическую природу. Он связан с факторами, влияющими на доходность ценных бумаг только отдельной компании. Специфические риски нейтрализуются противоположными изменениями доходностей других активов. Специфический риск – это диверсифицируемый риск. Слайд # 23 Челябинск 2010 Кафедра ЭТи. МЭ

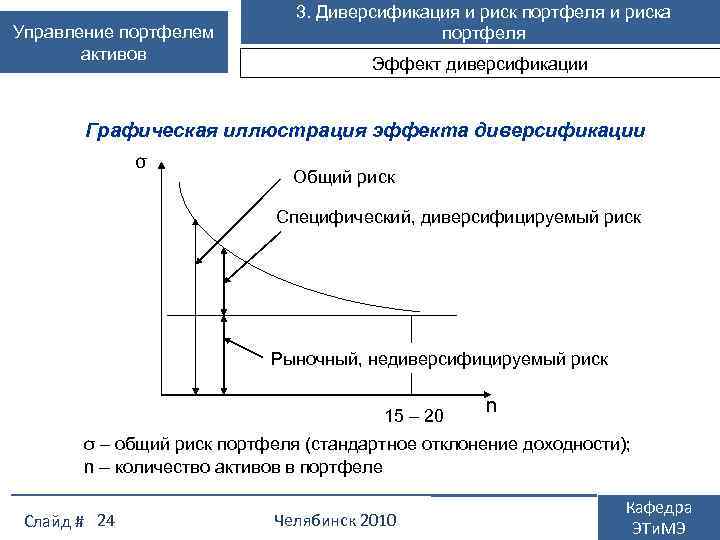Управление портфелем активов 3. Диверсификация и риск портфеля и риска портфеля Эффект диверсификации Графическая Управление портфелем активов 3. Диверсификация и риск портфеля и риска портфеля Эффект диверсификации Графическая иллюстрация эффекта диверсификации σ Общий риск Специфический, диверсифицируемый риск Рыночный, недиверсифицируемый риск 15 – 20 n σ – общий риск портфеля (стандартное отклонение доходности); n – количество активов в портфеле Слайд # 24 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Пределы эффективной диверсификации Теоретически возможно полное Управление портфелем активов 3. Диверсификация и риск портфеля Пределы эффективной диверсификации Теоретически возможно полное устранение специфического риска путем создания рыночного портфеля. Рыночный портфель – это набор активов, точно повторяющий состав и структуру рынка. Независимо от объема инвестированных средств доходность и риск такого портфеля соответствуют параметрам рынка в целом. Общий риск рыночного портфеля включает только рыночный риск. На практике столь широкая диверсификация не всегда возможна, так как инвесторам могут быть доступны далеко не все активы, присутствующие на рынке. Кроме того, существует предел эффективной диверсификации, превышение которого порождает отрицательный эффект. Слайд # 25 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Пределы эффективной диверсификации Отрицательные эффекты излишней Управление портфелем активов 3. Диверсификация и риск портфеля Пределы эффективной диверсификации Отрицательные эффекты излишней диверсификации возникают вследствие: невозможности качественного управления портфелем; включения в портфель низколиквидных активов; недостаточно доходных и роста издержек, связанных с поиском ценных бумаг (расходы на предварительный анализ и т. п. ); повышения трансакционных издержек при покупке небольших партий ценных бумаг. Слайд # 26 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Корреляция доходностей и эффект диверсификации Практика Управление портфелем активов 3. Диверсификация и риск портфеля Корреляция доходностей и эффект диверсификации Практика показывает, что включение в портфель порядка 15 20 ценных бумаг позволяет максимально использовать положительный эффект диверсификации и создать хорошо диверсифицированный портфель. Портфель считается хорошо диверсифицированным, если его специфический риск настолько мал, что им можно пренебречь. Количество активов, необходимое для создания хорошо диверсифицированного портфеля зависит от уровня корреляции ценных бумаг, включаемых в портфель. Чем меньше корреляция доходностей активов, тем больше эффект от их объединения в портфель. Слайд # 27 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Корреляция доходностей и эффект диверсификации Подсчитано, Управление портфелем активов 3. Диверсификация и риск портфеля Корреляция доходностей и эффект диверсификации Подсчитано, например, что вложение средств равными долями в любое количество акций с коэффициентом корреляции ρ = 0, 9 позволит снизить риск не более, чем на 5%. При коэффициенте корреляции 0, 8 такое снижение не превысит 10% При ρ = 0 вложение средств равными долями в акции 3 -х разных эмитентов приведет к снижению риска примерно на 40%. Слайд # 28 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Структура риска активов и эффект диверсификации Управление портфелем активов 3. Диверсификация и риск портфеля Структура риска активов и эффект диверсификации Результаты диверсификации портфеля зависят также от структуры риска ценных бумаг: 1. Чем выше доля специфического (диверсифицируемого) риска, тем больший эффект с точки зрения соотношения «доходность – риск» можно получить при создании портфеля. 2. Вклад каждого актива в общий риск хорошо диверсифицированного портфеля определяется уровнем его рыночного риска, так как специфический риск устраняется. Слайд # 29 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Коэффициент бета (β) Для измерения рыночного Управление портфелем активов 3. Диверсификация и риск портфеля Коэффициент бета (β) Для измерения рыночного риска активов используется коэффициент бета (β). Это относительный показатель, который определяет чувствительность доходности актива к изменениям доходности рынка. Бета ценных бумаг оценивается относительно рыночного портфеля на основе статистических данных по формулам: или где βi – бета i-го актива; covim– ковариация доходности i-го актива с доходностью рыночного портфеля; ρim – корреляция доходности i-го актива с доходностью рыночного портфеля; σ2 m и σm – соответственно дисперсия и стандартное отклонение рыночного портфеля Слайд # 30 Челябинск 2010 Кафедра ЭТи. МЭ

3. Диверсификация и риск портфеля Управление портфелем активов Бета портфеля (βp) При диверсификации портфеля 3. Диверсификация и риск портфеля Управление портфелем активов Бета портфеля (βp) При диверсификации портфеля рыночный риск активов не устраняется, а лишь усредняется. Бета портфеля – это средневзвешенное значение бета отдельных активов, входящих в портфель: Пример. Инвестор формирует портфель из четырех активов: A, B, C, D. A B C D βi 0, 8 0, 9 1, 2 1, 5 wi 0, 1 0, 4 0, 3 0, 2 βP = 0, 1· 0, 8 + 0, 4· 0, 9 + 0, 3· 1, 2 + 0, 2· 1, 5 = 1, 1 Слайд # 31 Челябинск 2010 Кафедра ЭТи. МЭ

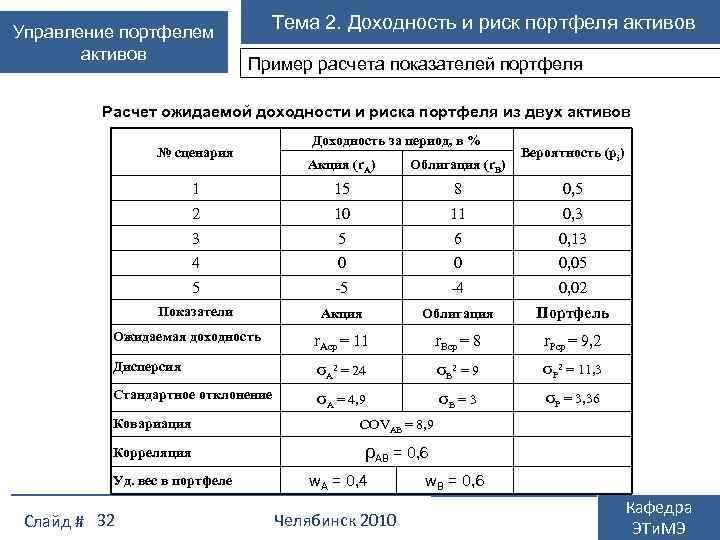Управление портфелем активов Тема 2. Доходность и риск портфеля активов Пример расчета показателей портфеля Управление портфелем активов Тема 2. Доходность и риск портфеля активов Пример расчета показателей портфеля Расчет ожидаемой доходности и риска портфеля из двух активов № сценария Доходность за период, в % Вероятность (pi) Акция (r. A) Облигация (r. B) 1 15 8 0, 5 2 10 11 0, 3 3 5 6 0, 13 4 0 0 0, 05 5 -5 -4 0, 02 Показатели Акция Облигация Портфель Ожидаемая доходность r. Aср = 11 r. Bср = 8 r. Pср = 9, 2 Дисперсия σA 2 = 24 σB 2 = 9 σP 2 = 11, 3 Стандартное отклонение σA = 4, 9 σB = 3 σP = 3, 36 Ковариация COVAB = 8, 9 Корреляция ρAB = 0, 6 Уд. вес в портфеле Слайд # 32 w. A = 0, 4 Челябинск 2010 w. B = 0, 6 Кафедра ЭТи. МЭ

3. Диверсификация и риск портфеля Управление портфелем активов 1. Пример расчета показателей портфеля • 3. Диверсификация и риск портфеля Управление портфелем активов 1. Пример расчета показателей портфеля • Расчет показателей доходности и риска активов (иллюстрируется расчет показателей доходности и риска акции, для облигации даются готовые данные). Ожидаемая (средневзвешенная) доходность акции • Дисперсия доходности акции • Стандартное отклонение Слайд # 33 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Пример расчета показателей портфеля 2. Расчет Управление портфелем активов 3. Диверсификация и риск портфеля Пример расчета показателей портфеля 2. Расчет показателей степени согласованности изменения доходности активов • Ковариация • Корреляция • Слайд # 34 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Диверсификация и риск портфеля Пример расчета показателей портфеля 3. Расчет Управление портфелем активов 3. Диверсификация и риск портфеля Пример расчета показателей портфеля 3. Расчет параметров портфеля при условии, что средства распределены между активами в пропорции 40: 60 • Доходность портфеля • Риск портфеля • Средневзвешенное стандартное отклонение активов, входящих в портфель • Размещение средств в двух активах с неполной корреляцией доходностей позволило сократить уровень риска по сравнению со средневзвешенной величиной Слайд # 35 Челябинск 2010 Кафедра ЭТи. МЭ

Южно-Уральский государственный университет Управление портфелем активов Тема 3. Теория выбора портфеля Моцаренко Наталья Васильевна Южно-Уральский государственный университет Управление портфелем активов Тема 3. Теория выбора портфеля Моцаренко Наталья Васильевна доцент кафедры «Экономическая теория и мировая экономика» Челябинск 2010

Управление портфелем активов Теория выбора портфеля 1. Выбор портфеля из рисковых активов. Оптимальный портфель. Управление портфелем активов Теория выбора портфеля 1. Выбор портфеля из рисковых активов. Оптимальный портфель. 2. Выбор портфеля при наличии на рынке безрискового актива. Теорема отделения. Слайд # 37 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Выбор портфеля из рискованных активов Предпосылки теории Теория выбора оптимального Управление портфелем активов 1. Выбор портфеля из рискованных активов Предпосылки теории Теория выбора оптимального портфеля из рискованных активов разработана Гарри Марковицем (1952 г. ). Теория основана на следующих предположениях о принципах поведения инвесторов при выборе портфеля: на решения инвестора влияют только два фактора – ожидаемая доходность и риск; инвесторы избегают риска, т. е. из двух вариантов инвестирования с одинаковой ожидаемой доходностью, но разными уровнями риска, они выбирают тот, риск которого меньше; при выборе портфеля инвесторы действуют рационально, стремясь максимизировать ожидаемую доходность при заданном уровне риска; ожидания инвесторов однородны, они имеют одинаковые взгляды на ожидаемую доходность и риск активов; существует одинаковый для всех инвестиционный горизонт, т. е. период для которого планируются инвестиции. Слайд # 38 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Выбор портфеля из рискованных активов Допустимое множество портфелей Из активов, Управление портфелем активов 1. Выбор портфеля из рискованных активов Допустимое множество портфелей Из активов, присутствующих на рынке можно создать множество портфелей, меняя состав портфеля и удельные веса ценных бумаг. Допустимое множество портфелей – совокупность всех портфелей, которые может создать инвестор из доступных ему активов. Допустимые портфели различаются по уровню доходности и риска. Поэтому перед инвестором стоит проблема выбора оптимального портфеля Вид допустимого множества зависит от корреляции активов. Для упрощения изложения это можно продемонстрировать на примере портфеля из двух активов. Слайд # 39 Челябинск 2010 Кафедра ЭТи. МЭ

1. Выбор портфеля из рискованных активов Управление портфелем активов при корреляции равной +1 допустимые 1. Выбор портфеля из рискованных активов Управление портфелем активов при корреляции равной +1 допустимые r • ρ = -1 А (акция) = ρ • B (облигация) Риск портфеля σр Допустимое множество портфелей из двух активов при различных коэффициентах корреляции Слайд # 40 портфели лежат на отрезке прямой АВ, т. к. доходность и риск активов портфеле усредняются. Эффект диверсификации отсутствует; при корреляции равной -1 допустимые портфели лежат на отрезках АС и ВС, т. к. доходность активов портфеле усредняется, а риск уменьшается. Возможно создание безрискового портфеля «С» ; +1 0, 9 ρ= 0 ρ= С • 0, 5 ρ = -1 ρ =- Ожидаемая доходность портфеля Допустимое множество портфелей из двух активов при неполной корреляции доходность активов в портфеле усредняется, а риск уменьшается. Допустимое множество располагается на отрезках кривых внутри треугольника АВС. Эффект диверсификации тем больше, чем меньше коэффициент корреляции. Челябинск 2010 Кафедра ЭТи. МЭ

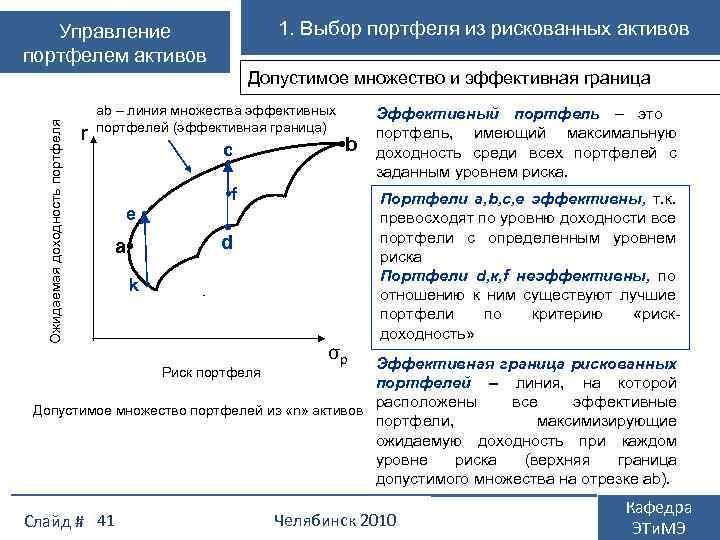1. Выбор портфеля из рискованных активов Управление портфелем активов Ожидаемая доходность портфеля Допустимое множество 1. Выбор портфеля из рискованных активов Управление портфелем активов Ожидаемая доходность портфеля Допустимое множество и эффективная граница r ab – линия множества эффективных портфелей (эффективная граница) c • e • a • • b • f • d k • σр Эффективный портфель – это портфель, имеющий максимальную доходность среди всех портфелей с заданным уровнем риска. Портфели a, b, c, e эффективны, т. к. превосходят по уровню доходности все портфели с определенным уровнем риска Портфели d, к, f неэффективны, по отношению к ним существуют лучшие портфели по критерию «рискдоходность» Эффективная граница рискованных портфелей – линия, на которой расположены все эффективные Допустимое множество портфелей из «n» активов портфели, максимизирующие ожидаемую доходность при каждом уровне риска (верхняя граница допустимого множества на отрезке ab). Риск портфеля Слайд # 41 Челябинск 2010 Кафедра ЭТи. МЭ

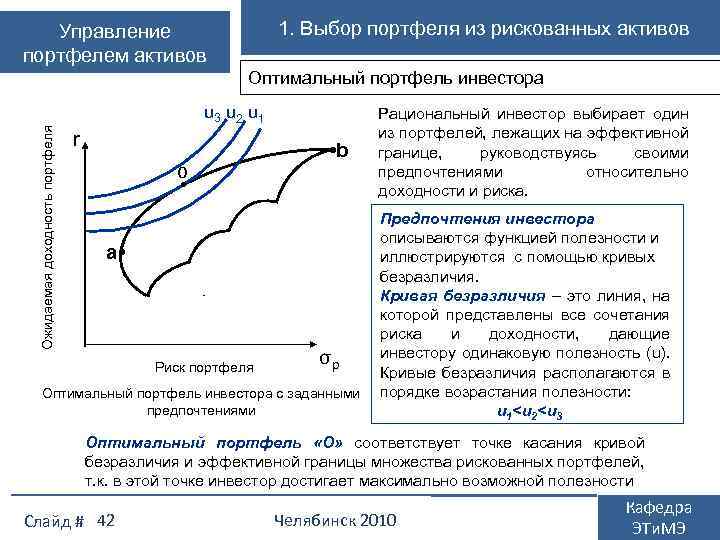1. Выбор портфеля из рискованных активов Управление портфелем активов Оптимальный портфель инвестора Ожидаемая доходность 1. Выбор портфеля из рискованных активов Управление портфелем активов Оптимальный портфель инвестора Ожидаемая доходность портфеля u 3 u 2 u 1 r о • • b a • Риск портфеля σр Оптимальный портфель инвестора с заданными предпочтениями Рациональный инвестор выбирает один из портфелей, лежащих на эффективной границе, руководствуясь своими предпочтениями относительно доходности и риска. Предпочтения инвестора описываются функцией полезности и иллюстрируются с помощью кривых безразличия. Кривая безразличия – это линия, на которой представлены все сочетания риска и доходности, дающие инвестору одинаковую полезность (u). Кривые безразличия располагаются в порядке возрастания полезности: u 1

Управление портфелем активов 2. Выбор портфеля при наличии на рынке безрискового актива Безрисковый актив: Управление портфелем активов 2. Выбор портфеля при наличии на рынке безрискового актива Безрисковый актив: определение Безрисковый актив – это актив, доходность которого фиксирована и известна в начале периода владения данным активом. Безрисковыми являются, например, государственные краткосрочные облигации, если инвестор планирует держать их до погашения, а также банковские депозиты по фиксированной ставке. Для упрощения предполагается, что: существует безрисковый актив с одинаковой для всех инвесторов доходностью; инвестор может размещать и привлекать средства по безрисковой ставке. Слайд # 43 Челябинск 2010 Кафедра ЭТи. МЭ

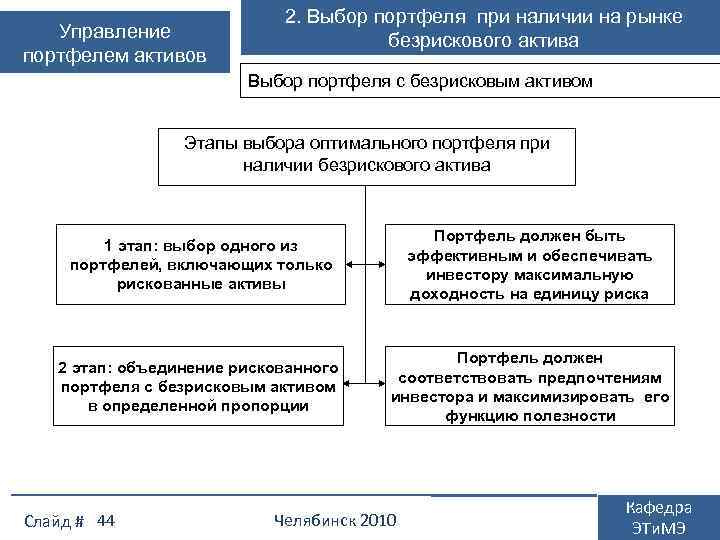Управление портфелем активов 2. Выбор портфеля при наличии на рынке безрискового актива Выбор портфеля Управление портфелем активов 2. Выбор портфеля при наличии на рынке безрискового актива Выбор портфеля с безрисковым активом Этапы выбора оптимального портфеля при наличии безрискового актива 1 этап: выбор одного из портфелей, включающих только рискованные активы Портфель должен быть эффективным и обеспечивать инвестору максимальную доходность на единицу риска 2 этап: объединение рискованного портфеля с безрисковым активом в определенной пропорции Портфель должен соответствовать предпочтениям инвестора и максимизировать его функцию полезности Слайд # 44 Челябинск 2010 Кафедра ЭТи. МЭ

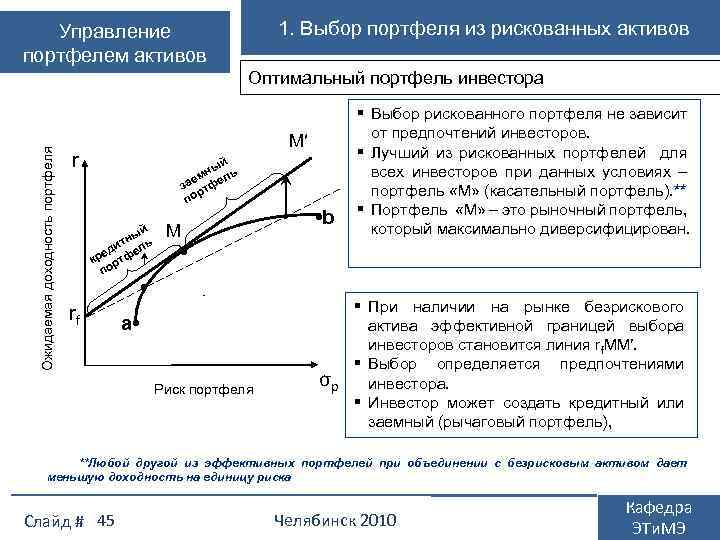1. Выбор портфеля из рискованных активов Управление портфелем активов Ожидаемая доходность портфеля Оптимальный портфель 1. Выбор портфеля из рискованных активов Управление портфелем активов Ожидаемая доходность портфеля Оптимальный портфель инвестора M′ r й ны ль ем за тфе р по ый тн ль ди ре тфе к р по M • b • • rf • Выбор рискованного портфеля не зависит от предпочтений инвесторов. Лучший из рискованных портфелей для всех инвесторов при данных условиях – портфель «М» (касательный портфель). ** Портфель «М» – это рыночный портфель, который максимально диверсифицирован. a • Риск портфеля При наличии на рынке безрискового актива эффективной границей выбора инвесторов становится линия rf. MM′. Выбор определяется предпочтениями σр инвестора. Инвестор может создать кредитный или заемный (рычаговый портфель), **Любой другой из эффективных портфелей при объединении с безрисковым активом дает меньшую доходность на единицу риска Слайд # 45 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Выбор портфеля при наличии на рынке безрискового актива Теорема отделения Управление портфелем активов 2. Выбор портфеля при наличии на рынке безрискового актива Теорема отделения (инвестирования в два фонда) Теорема (свойство) отделения впервые сформулировано Джеймсом Тобином (1958 г. ): Выбор портфеля при наличии безрискового актива разделяется на две независимые задачи. Первая задача – определение оптимального рискованного портфеля – представляет собой чисто техническую задачу. Оптимальный портфель будет одинаков для всех инвесторов независимо от их предпочтений. Вторая задача – формирование портфеля из безрискового актива и оптимального портфеля рискованных активов – зависит от предпочтений участников рынка. В данном случае решение принимает каждый инвестор индивидуально. Слайд # 46 Челябинск 2010 Кафедра ЭТи. МЭ

Южно-Уральский государственный университет Управление портфелем активов Тема 4. Теория рынка капитала и оценка стоимости Южно-Уральский государственный университет Управление портфелем активов Тема 4. Теория рынка капитала и оценка стоимости капитальных активов Моцаренко Наталья Васильевна доцент кафедры «Экономическая теория и мировая экономика» Челябинск 2010

Управление портфелем активов Теория рынка капитала и оценка стоимости капитальных активов 1. Модель оценки Управление портфелем активов Теория рынка капитала и оценка стоимости капитальных активов 1. Модель оценки стоимости капитальных активов (CAPM) 2. Рыночная (индексная)модель У. Шарпа Слайд # 48 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов Тема 4. Теория рынка капитала и оценка стоимости капитальных активов 1. Управление портфелем активов Тема 4. Теория рынка капитала и оценка стоимости капитальных активов 1. Модель оценки стоимости капитальных активов (CAPM) Аббревиатура САРМ расшифровывается как модель ценообразования капитальных активов (Capital Asset Pricing model) Модель была разработана рядом крупных исследователей финансового рынка, прежде всего, лауреатом Нобелевской премии Уильямом Шарпом, а также Джоном Линтнером и Джеком Трейнором. При выполнении некоторых предположений о характере фондового рынка САРМ позволяет оценить ожидаемую ( «требуемую» ) доходность портфеля или отдельного актива, которой они должны иметь в зависимости от ожидаемой доходности рынка и уровня риска. Слайд # 49 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Предпосылки САРМ строится на Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Предпосылки САРМ строится на ряде предпосылок (упрощений), которые определяют сферу ее действия. При выводе САРМ были сделаны следующие допущения: • инвестор руководствуется только двумя факторами – доходностью и риском; • инвесторы действуют рационально; • ожидания инвесторов одинаковы, так как формируются на основе доступной всем информации; • поведение индивидуального инвестора на влияет на равновесные цены активов; • нет трансакционных издержек, препятствующих свободному формированию спроса и предложения активов; • рынок эффективен, вся информация немедленно отражается в цене активов. Слайд # 50 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Сфера действия САРМ Из Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Сфера действия САРМ Из принятых при формировании САРМ предпосылок следует, что: • эта модель, построена для эффективного рынка, находящегося в состоянии равновесия; • это нормативная модель, которая показывает какой должна быть ожидаемая доходность актива в зависимости от состояния рынка и риска актива; • это модель – эталон, относительно которого определяется, насколько точно рынок оценивает конкретный актив в данный момент времени; • CAPM определяет величину премии за риск, которая должна включаться в доходность актива при оценке его действительной стоимости. Слайд # 51 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) САРМ: линия рынка капитала Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) САРМ: линия рынка капитала (CML) Линия рынка капитала в САРМ – это модель, которая определяет ожидаемую доходность эффективных портфелей ценных бумаг, расположенных на эффективной границе допустимого множества портфелей при наличии на рынке безрискового актива. Эффективные портфели полностью диверсифицированы и подвержены только рыночному риску. Показатель риска эффективного портфеля – стандартное отклонение специфического риска. – не содержит Поэтому линия рынка капитала строится в координатах «стандартное отклонение – доходность» . Слайд # 52 Челябинск 2010 Кафедра ЭТи. МЭ

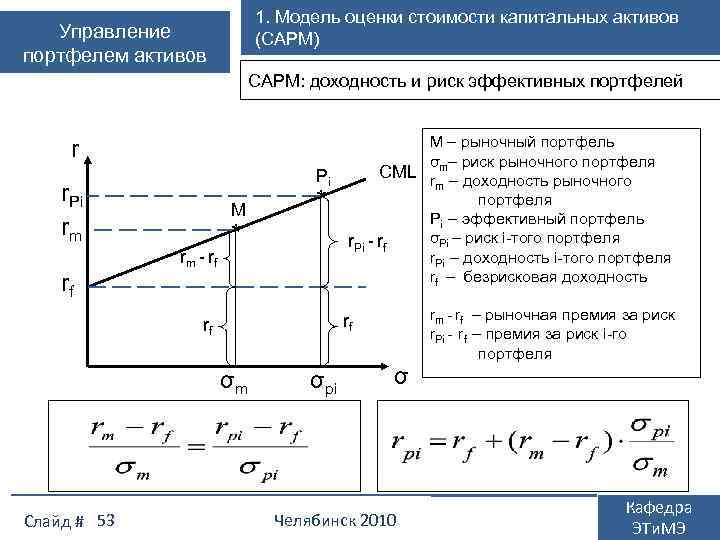1. Модель оценки стоимости капитальных активов (CAPM) Управление портфелем активов CAPM: доходность и риск 1. Модель оценки стоимости капитальных активов (CAPM) Управление портфелем активов CAPM: доходность и риск эффективных портфелей r Pi rm rf M rm - rf * * rf rf σm Слайд # 53 M – рыночный портфель σ – риск рыночного портфеля CML r m – доходность рыночного m портфеля Pi – эффективный портфель σPi – риск i-того портфеля r. Pi - rf r. Pi – доходность i-того портфеля rf – безрисковая доходность σpi σ Челябинск 2010 rm - rf – рыночная премия за риск r. Pi - rf – премия за риск i-го портфеля Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) САРМ: рыночная цена риска Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) САРМ: рыночная цена риска Формула определения ожидаемой доходности эффективного портфеля (см. слайд 18) представляет собой уравнение линии рынка капитала, угловой коэффициент которого количественно определяет рыночную цену риска, сложившуюся в данный момент времени: Цена риска определяет величину дополнительной доходности, которую может получить инвестор, приняв на себя дополнительную единицу риска. Цена риска зависит от состояния и структуры рынка, уровня безрисковой доходности и ожиданий инвесторов. Слайд # 54 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) САРМ: линия рынка ценных Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) САРМ: линия рынка ценных бумаг (SML) Линия рынка ценных бумаг в САРМ – это модель, которая определяет ожидаемую доходность неэффективных (не достаточно диверсифицированных) портфелей, а также отдельных ценных бумаг. Эти активы подвержены не только рыночному, но и специфическому риску. Из теории портфеля следует: • специфический риск может быть устранен диверсификацией инвестиций; • премия за риск должна определяться только рыночным риском. Поэтому линия рынка ценных бумаг строится в координатах «рыночный риск активов (β) – доходность» . Слайд # 55 Челябинск 2010 Кафедра ЭТи. МЭ

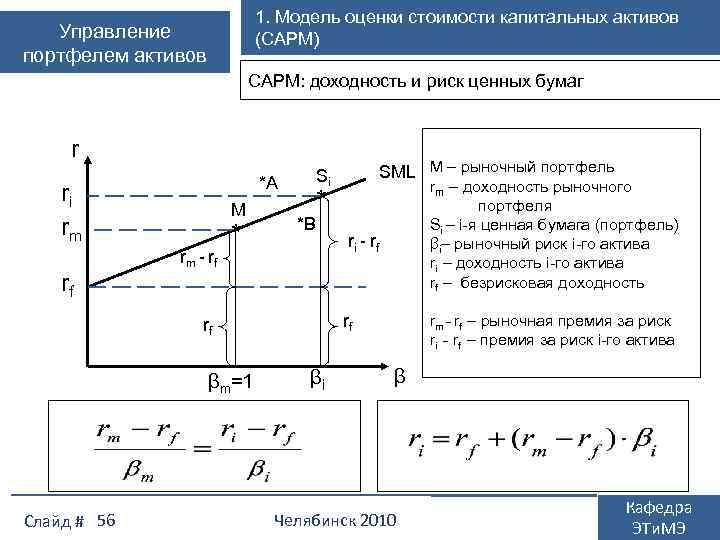1. Модель оценки стоимости капитальных активов (CAPM) Управление портфелем активов CAPM: доходность и риск 1. Модель оценки стоимости капитальных активов (CAPM) Управление портфелем активов CAPM: доходность и риск ценных бумаг r *А ri rm rf M rm - rf * Слайд # 56 rm – доходность рыночного портфеля Si – i-я ценная бумага (портфель) βi– рыночный риск i-го актива ri – доходность i-го актива rf – безрисковая доходность * *В ri - rf rf rf βm=1 SML M – рыночный портфель Si βi rm - rf – рыночная премия за риск ri - rf – премия за риск i-го актива β Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Пример 1. Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Пример 1. Оценка ожидаемой (требуемой) доходности эффективного портфеля Исходные данные: Рыночный портфель: ожидаемая доходность rm= 15% риск σm= 10% Эффективный портфель: риск σP 1= 16% σP 2= 8% Ставка доходности без риска Решение: rf = 5% Цена риска = ? r. Pi = ? Цена риска = (15% - 5%) / 10% = 1% r. P 1 = 5% + (15% – 5%)·(16%/10%) = 21% r. P 2 = 5% + (15% – 5%)·(8%/10%) = 13% Слайд # 57 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Пример 2. Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Пример 2. Оценка ожидаемой (требуемой) доходности акций Исходные данные: Ожидаемая доходность рынка: rm= 15% Рыночный риск акций β 1 = 1, 5 β 2 = 0, 8 Ставка доходности без риска Решение: ri = ? rf = 5% r 1 = 5% + (15% – 5%)· 1, 5 = 20% r 2 = 5% + (15% – 5%)· 0, 8 = 13% Слайд # 58 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Выводы: Если Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Выводы: Если ожидаемая доходность акции, рассчитанная по историческим данным окажется выше доходности по САРМ*, то акция считается недооцененной рынком, ее рыночная цена ниже равновесной и в будущем может вырасти. Недооцененная акция представляет интерес для включения в портфель. Если ожидаемая доходность акции, рассчитанная по историческим данным окажется ниже доходности по САРМ**, то акция считается переоцененной рынком, ее рыночная цена выше равновесной и в будущем может снизиться. Переоцененная акция не представляет интереса для включения в портфель. * Акция по уровню доходности расположена над линией SML (слайд 21; *А) ** Акция по уровню доходности расположена над линией SML (слайд 21; *В) Слайд # 59 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Положения CAPM Управление портфелем активов 1. Модель оценки стоимости капитальных активов (CAPM) Применение САРМ Положения CAPM могут быть использованы для оценки инвестиционной привлекательности ценных бумаг. В частности, при определении возможности финансирования реальных инвестиционных проектов фирм за счет дополнительной эмиссии акций. В этом случае сопоставляется уровень доходности акций, которого ожидают инвесторы и уровень доходности инвестиционного проекта. Пример 3. Компания предполагает реализовать инвестиционный проект с внутренней нормой окупаемости IRR=14%. Для финансирования проекта планируется дополнительная эмиссия акций. Коэффициент β для акций данной компании составляет 1, 3 Рыночная доходность rm = 12%, ставка доходности без риска rf = 4% Решение: Доходность акций, ожидаемая инвесторами в соответствии с CAPM (в %): r*= 4 + (12 – 4)· 1, 3 = 14, 4 Требуемая инвесторами доходность акций (r* = 14, 4%) больше внутренней нормы окупаемости проекта (IRR = 14%). Акционеры не поддержат проект. Слайд # 60 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов Тема 4. Теория рынка капитала и оценка доходности капитальных активов 2. Управление портфелем активов Тема 4. Теория рынка капитала и оценка доходности капитальных активов 2. Рыночная (индексная) модель У. Шарпа Индексная модель Шарпа так же как и CAPM предназначена для оценки ожидаемой доходности рыночных активов. В отличие от CAPM, которая является нормативной моделью, модель Шарпа – это позитивная модель, в которой выявляется фактически существующая зависимость между доходностью ценных бумаг и доходностью рынка. Модель называется индексной, так как в ней в качестве «представителя» рынка используется какой-либо рыночный индекс. Преимущество индексной модели в том, что состав индекса четко определен, а его изменения непосредственно наблюдаются. Слайд # 61 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Сфера действия модели Индексная модель Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Сфера действия модели Индексная модель Шарпа используется для: • определения статистической зависимости между избыточной доходностью рыночного индекса, представляющей рыночную премию за риск, и избыточной доходностью актива (фактической премией за риск ценной бумаги); • выявления переоцененных или недооцененных ценных бумаг; • количественной оценки влияния систематического и специфического риска на доходность актива; • оценки достаточности уровня диверсификации портфеля с точки зрения нейтрализации специфического риска. Слайд # 62 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Математическое описание модели Шарпа Уравнение Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Математическое описание модели Шарпа Уравнение модели Шарпа имеет вид: Ri = αi + βi∙Rm + εi , где Ri – избыточная доходность акции (фактически полученная премия за риск); Ri – избыточная доходность индекса; αi – нерыночная составляющая доходности акции, т. е. доходность, которую она имеет в отсутствие влияния рыночных факторов; βi – чувствительность доходности акции к изменениям рыночной доходности ( представленной доходностью индекса); εi – компонент доходности, связанный с неожиданными событиями, касающимися только этой акции. Параметры модели оцениваются статистически с помощью регрессионного анализа, что и позволяет выявить существующую зависимость доходности акции от рыночной доходности. Слайд # 63 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Структура риска активов Уравнение модели Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Структура риска активов Уравнение модели Шарпа (см. слайд 28) указывает на два источника риска акций: 1. Рыночный риск ( βi∙Rm), относящийся к «движениям» рынка в целом; 2. Специфический риск ( εi ), который является частью общего риска и не зависит от рыночного фактора. Дисперсию доходности акции можно представить следующим образом: σ2( Ri ) = σ2( αi + βi∙Rm + εi ) или σ2( Ri ) = βi 2σ2( Rm) + σ2( εi ), где: выражение βi 2σ2(Rm) определяет рыночный риск; выражение σ2(εi) – специфический риск. Слайд # 64 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Структура риска активаов Доля рыночного Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Структура риска активаов Доля рыночного риска в общем риске ценной бумаги определяется коэффициентом детерминации: Коэффициент детерминации** показывает, какая доля общего риска (дисперсии доходности) ценной бумаги объясняется изменениями доходности рынка. Пример: ρ2 акции равен 0, 49. Это значит, что изменение доходности акции на 49% можно объяснить изменением доходности рынка, в то же время доля специфического риска в общем риске акции составляет 51%. Эта часть риска может быть устранена в процессе диверсификации портфеля ** Коэффициент детерминации обозначается ρ2, так его значение соответствует квадрату коэффициента корреляции между доходностью акции и рыночной доходностью. Слайд # 65 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Коэффициент детерминации портфеля Коэффициент детерминации Управление портфелем активов 2. Рыночная (индексная) модель У. Шарпа Коэффициент детерминации портфеля Коэффициент детерминации может быть оценен и для портфеля в целом. Он позволяет оценить уровень его диверсификации. ρ-квадрат широко диверсифицированного портфеля может составлять 0, 9 и большую величину, так как специфический риск такого портфеля близок к нулю. Слайд # 66 Челябинск 2010 Кафедра ЭТи. МЭ

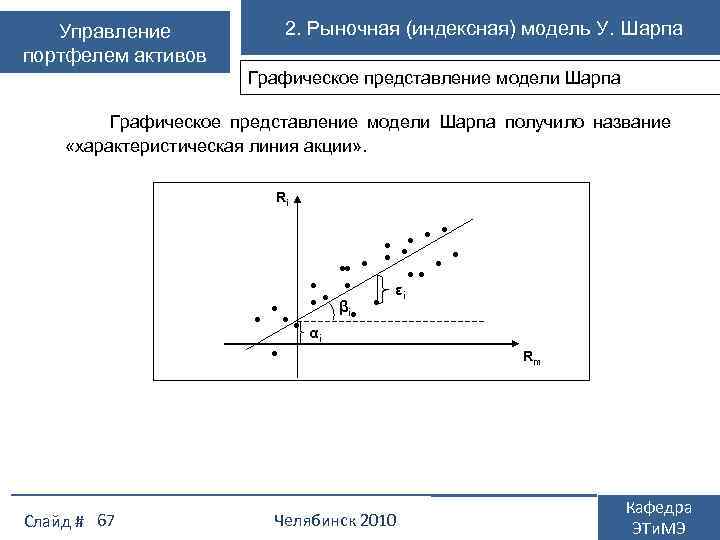2. Рыночная (индексная) модель У. Шарпа Управление портфелем активов Графическое представление модели Шарпа получило 2. Рыночная (индексная) модель У. Шарпа Управление портфелем активов Графическое представление модели Шарпа получило название «характеристическая линия акции» . Ri • • • Слайд # 67 • • • • • • • εi • • βi • • αi Челябинск 2010 Rm Кафедра ЭТи. МЭ

Южно-Уральский государственный университет Управление портфелем активов Тема 5. Формирование портфеля (практикум по применению теории Южно-Уральский государственный университет Управление портфелем активов Тема 5. Формирование портфеля (практикум по применению теории портфеля) Моцаренко Наталья Васильевна доцент кафедры «Экономическая теория и мировая экономика» Челябинск

Управление портфелем активов Формирование портфеля (практикум) 1. Выбор структуры портфеля из рискованного и безрискового Управление портфелем активов Формирование портфеля (практикум) 1. Выбор структуры портфеля из рискованного и безрискового активов с учетом предпочтений инвестора 2. Формирование оптимального портфеля из двух безрисковых активов 3. Распределение средств между портфелем активов с риском и безрисковым активом Слайд # 69 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Исходные данные Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Исходные данные Рассмотрим задачу составления портфеля из двух активов (рискованного и безрискового) с учетом требуемой инвестором доходности или ограничений по риску при следующих условиях: • объем инвестируемых средств составляет 100 ден. ед. ; • доходность безрискового актива rf = 6%; • рискованный актив (акция) имеет ожидаемую доходность rs = 14%; • стандартное отклонение акции σS = 20% Параметры допустимого множества портфелей из доступных инвестору активов можно рассчитать по формулам: Доходность: Риск : rp = rs∙ ws + rf∙ wf σp = σS· ws (1) (2) Результаты расчета параметров портфеля с шагом изменения удельного веса активов 25% можно представить в таблице, предполагая возможность формирования заемного портфеля Слайд # 70 Челябинск 2010 Кафедра ЭТи. МЭ

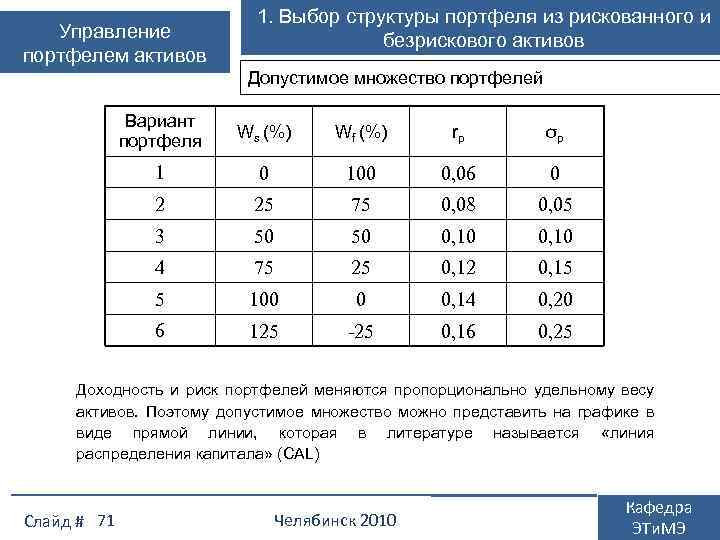Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Допустимое множество Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Допустимое множество портфелей Вариант портфеля Ws (%) Wf (%) rp σp 1 0 100 0, 06 0 2 25 75 0, 08 0, 05 3 50 50 0, 10 4 75 25 0, 12 0, 15 5 100 0 0, 14 0, 20 6 125 -25 0, 16 0, 25 Доходность и риск портфелей меняются пропорционально удельному весу активов. Поэтому допустимое множество можно представить на графике в виде прямой линии, которая в литературе называется «линия распределения капитала» (CAL) Слайд # 71 Челябинск 2010 Кафедра ЭТи. МЭ

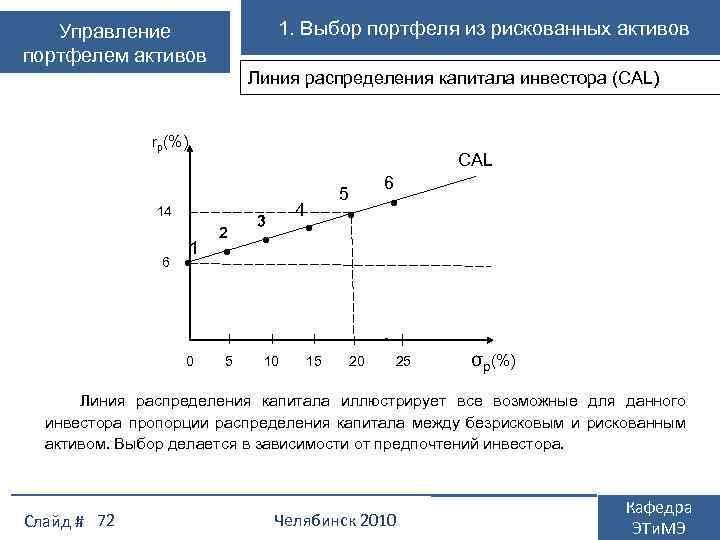1. Выбор портфеля из рискованных активов Управление портфелем активов Линия распределения капитала инвестора (CAL) 1. Выбор портфеля из рискованных активов Управление портфелем активов Линия распределения капитала инвестора (CAL) rp(%) CAL 14 6 1 • 0 2 • 5 4 3 • • 10 6 5 15 • 20 • 25 σp(%) Линия распределения капитала иллюстрирует все возможные для данного инвестора пропорции распределения капитала между безрисковым и рискованным активом. Выбор делается в зависимости от предпочтений инвестора. Слайд # 72 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Определение структуры Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Определение структуры портфеля с заданной доходностью На основе формул (1) и (2) можно определить структуру портфеля с любой заданной доходностью. Подставив в формулу (1) выражение удельного веса безрискового актива как wf = 1 – ws, получим: rp = rf + (rs - rf) ws (3) (4) Если инвестор ориентируется на получение ожидаемой доходности 9%, то, подставив это значение и другие исходные данные в формулу (4), получим: Таким образом, для получения заданной доходности при имеющихся возможностях инвестирования следует распределить средства следующим образом: 37, 5% вложить в акцию, а 62, 5 % - в безрисковый актив по фиксированной ставке. Слайд # 73 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Оценка риска Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Оценка риска предполагаемого портфеля Риск предполагаемого портфеля можно оценить по формуле (2) : σp = σS· ws = 20∙ 0, 375 = 7, 5% Если инвестор готов принять данный уровень риска, он создает портфель. В противном случае он должен пересмотреть свои требования относительно ожидаемой доходности. На основе исходных формул можно исключить удельный вес активов, чтобы напрямую связать риск и доходность формируемого портфеля. Для этого из формулы (2) выражаем удельный вес и подставляем его в формулу (3): σp = σS· ws → rp = rf + (rs - rf)· Слайд # 74 Челябинск 2010 (5) Кафедра ЭТи. МЭ

Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Оценка риска Управление портфелем активов 1. Выбор структуры портфеля из рискованного и безрискового активов Оценка риска предполагаемого портфеля Формула определения доходности портфеля (5) является уравнением линии распределения капитала для данного инвестора (см. слайд 5). При этом выражение определяет угол наклона этой линии, а с финансовой точки зрения представляет собой цену риска, которую обеспечивает инвестору выбранный им набор финансовых инструментов. Цена риска – это дополнительная доходность, которую может получить инвестор, приняв дополнительную единицу риска и изменив структуру портфеля в пользу рискованного актива. Для данного инвестора цена риска составляет: Иными словами, увеличивая риск (стандартное отклонение портфеля) на 1% за счет перераспределения своих средств, инвестор получает дополнительно 0, 4% ожидаемой доходности. если такая цена риска его не устраивает, он должен выбрать более рискованный актив для составления портфеля. Слайд # 75 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Формирование оптимального портфеля из двух рискованных активов Исходные данные Рассмотрим Управление портфелем активов 2. Формирование оптимального портфеля из двух рискованных активов Исходные данные Рассмотрим задачу составления портфеля из двух рискованных активов при следующих условиях: • доходность безрискового актива rf = 6%; • актив 1 (акция) имеет ожидаемую доходность r 1 = 14% и отклонение σ1 = 20%; стандартное • актив 2 (облигация) имеет ожидаемую доходность r 2 = 8% и отклонение σ1 = 15%; стандартное • корреляция доходностей активов ρ = 0 Параметры допустимого множества портфелей из доступных инвестору активов можно рассчитать по формулам, меняя удельные веса активов: Доходность r p = r 1 ∙ w 1 + r 2 ∙ w 2 Риск Слайд # 76 (1) (2) Челябинск 2010 Кафедра ЭТи. МЭ

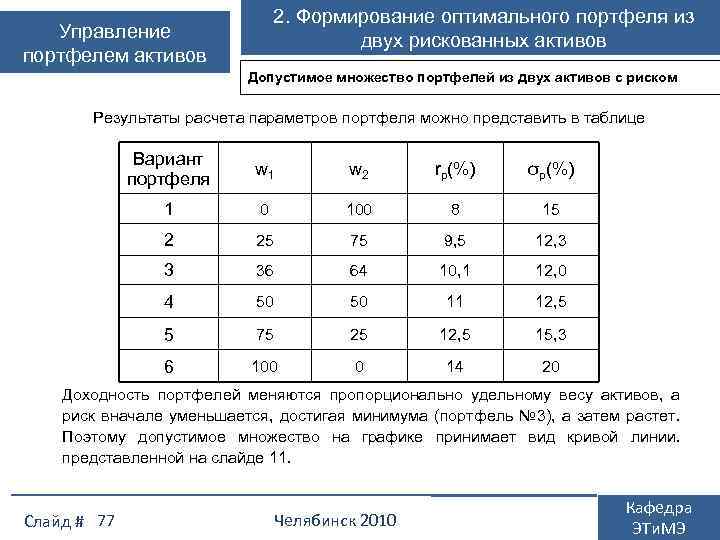2. Формирование оптимального портфеля из двух рискованных активов Управление портфелем активов Допустимое множество портфелей 2. Формирование оптимального портфеля из двух рискованных активов Управление портфелем активов Допустимое множество портфелей из двух активов с риском Результаты расчета параметров портфеля можно представить в таблице Вариант портфеля w 1 w 2 rp(%) σp(%) 1 0 100 8 15 2 25 75 9, 5 12, 3 3 36 64 10, 1 12, 0 4 50 50 11 12, 5 5 75 25 12, 5 15, 3 6 100 0 14 20 Доходность портфелей меняются пропорционально удельному весу активов, а риск вначале уменьшается, достигая минимума (портфель № 3), а затем растет. Поэтому допустимое множество на графике принимает вид кривой линии. представленной на слайде 11. Слайд # 77 Челябинск 2010 Кафедра ЭТи. МЭ

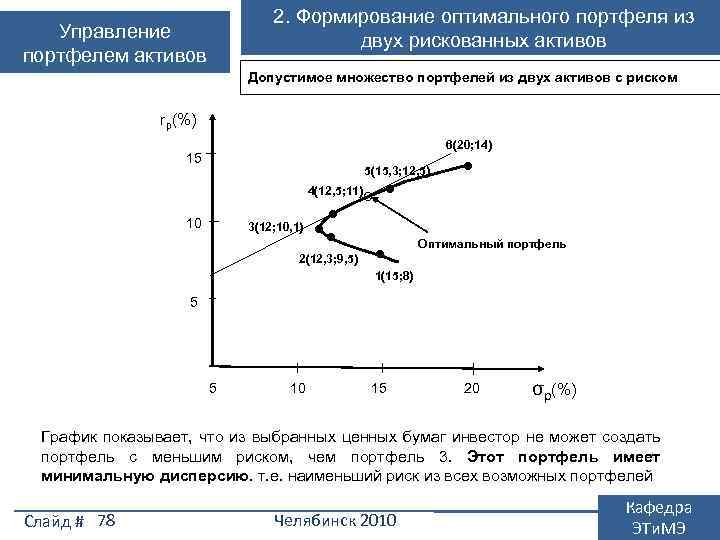2. Формирование оптимального портфеля из двух рискованных активов Управление портфелем активов Допустимое множество портфелей 2. Формирование оптимального портфеля из двух рискованных активов Управление портфелем активов Допустимое множество портфелей из двух активов с риском rp(%) 6(20; 14) 15 5(15, 3; 12, 5) 4(12, 5; 11) 10 3(12; 10, 1) • • • 2(12, 3; 9, 5) ○ • • • Оптимальный портфель 1(15; 8) 5 5 10 15 20 σp(%) График показывает, что из выбранных ценных бумаг инвестор не может создать портфель с меньшим риском, чем портфель 3. Этот портфель имеет минимальную дисперсию. т. е. наименьший риск из всех возможных портфелей Слайд # 78 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Формирование оптимального портфеля из двух рискованных активов Определение портфеля с Управление портфелем активов 2. Формирование оптимального портфеля из двух рискованных активов Определение портфеля с минимальной дисперсией Структура портфеля с минимальной дисперсией находится по формуле*: *Формула выводится методом дифференциации выражения для риска портфеля в зависимости от удельного веса активов (см. формулу 2, слайд 9) и приравнивания первой производной нулю. В данном случае математическое решение задачи опускается. Формула может использоваться при выполнении заданий контрольной работы. Слайд # 79 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 2. Формирование оптимального портфеля из двух рискованных активов Определение портфеля с Управление портфелем активов 2. Формирование оптимального портфеля из двух рискованных активов Определение портфеля с минимальной дисперсией Согласно теории инвестор стремится сформировать оптимальный портфель. который обеспечивал бы ему максимизацию доходности на единицу риска. Такой портфель не зависит от предпочтений инвестора и будет одинаковым для всех инвесторов, формирующих портфель из тех же активов. Оптимальный портфель находится в точке касания линии, проведенной из уровня безрисковой доходности и линии допустимого множества портфелей (см. тему 3, слайд 15). Для определения оптимального портфеля из двух активов используется формула (математический вывод опускается): Подставив исходные данные в формулу можно определить удельные веса акции и облигации в оптимальном портфеле: w 1 = 69, 2%; w 2 = 30, 8%. С учетом удельных весов определяется доходность и риск оптимального портфеля. Доходность (слайд 9. формула 1) будет равна 12, 2%, а риск – 14, 4% Слайд # 80 Челябинск 2010 Кафедра ЭТи. МЭ

Управление портфелем активов 3. Распределение средств между портфелем активов с риском и безрисковым вложением Управление портфелем активов 3. Распределение средств между портфелем активов с риском и безрисковым вложением Определение структуры портфеля с заданной доходностью Теперь можно предположить, что инвестор желает разместить средства как в рискованном портфеле, так и в безрисковом активе (доходность по-прежнему 6%). Он ориентируется на ожидаемую доходность совокупного портфеля 10%. По алгоритму, представленному в 1 вопросе, можно рассчитать необходимую структуру совокупного портфеля и оценить его риск. При определении удельного веса рискованных вложений вместо отдельной ценной бумаги теперь рассматривается оптимальный портфель с доходностью 12, 2% и риском 14, 4%. Удельные веса рассчитываются по формуле 4 (слайд 6) Таким образом, из общего объема инвестиций 100 ден. ед. в портфеле с риском размещается 65 ден. ед. , в безрисковом активе 35 ден. ед. 65 ден. ед. распределяются между акцией и облигацией в соответствии с их удельными весами в оптимальном портфеле: Слайд # 81 Челябинск 2010 Кафедра ЭТи. МЭ