Югорский государственный университет Основы математического моделирования социально-экономических процессов

Югорский государственный университет Основы математического моделирования социально-экономических процессов Семенов Сергей Петрович, канд. физ. - мат. наук, доцент кафедры КМИТ, т. 357 -715, каб. 203/6, ssp@ugrasu. ru

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ Лекции – 6 часов Лабораторные работы – 6 часов Отчетность – зачет Самостоятельная работа ssp@ugrasu. ru 2

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ Ранее изученные дисциплины: Микроэкономика Макроэкономика Высшая математика: Линейная алгебра Аналитическая геометрия Математический анализ Линейное программирование ssp@ugrasu. ru 3

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ Преподавание данной дисциплины имеет целью: • обучение основным принципам построения моделей, необходимых для анализа процессов и явлений экономического и управленческого характера; • формирование способностей к логическому и алгоритмическому мышлению. ssp@ugrasu. ru 4

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГРАММА Введение. Методология математического моделирования экономических систем и явлений Тема 1. Модели потребления Тема 2. Модели производства Тема 3. Модели экономического взаимодействия на простейших рынках Тема 4. Модели управления запасами Тема 5. Модели межотраслевого баланса ssp@ugrasu. ru 5

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ Основная литература 1. 2. 3. 4. 5. 6. 7. Малыхин В. И. Математическое моделирование экономики. М. , 1998. Интрилигатор М. Математические методы оптимизации и экономическая теория. Пер. с англ. – М. , 1975. Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе. - М. : ЮНИТИ-ДАНА, 2000. Вэриан Х. Р. Микроэкономика. Промежуточный уровень, современный подход: пер. с англ. М. , «ЮНИТИ» , 1997. Мур Дж. Х. , Уэдерфорд Л. Р. Экономическое моделирование в MICROSOFT EXCEL, 6 -е издание: пер. с англ. , 2004 г. , 1024 стр. Данилов Н. Н. Курс математической экономики: Учеб. пособие. – М. : Высш. шк. . 2006. – 407 с. , Ашманов С. А. Введение в математическую экономику. – М. : Наука, 1984 ssp@ugrasu. ru 6

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ Дополнительная литература 1. 2. 3. 4. 5. 6. 7. Карасев А. И. , Кремер Н. Ш. , Савельева Т. И. Математические методы и модели в планировании. – М. , 1987. Колемаев В. А. Математическая экономика: учеб. для вузов. 2 -е изд. , перераб. и доп. - М. : ЮНИТИ-ДАНА, 2002. Красс М. С. , Чупырнов Б. П. Основы математики и ее приложения в экономическом образовании. - 3 -е изд. , испр. М. : Дело, 2002. Красс М. С. Высшая математика для экономистов. - 4 -е изд. , испр. - М. : Дело, 2003 Сидоренко М. Г. Математические модели в экономике. Учебное пособие. Томск, 2000. Трояновский В. М. Элементы математического моделирования в макроэкономике/. - М. : РДЛ, 2001. Черник Д. Г. Введение в экономико-математические модели налогообложения. - М. : Финансы и статистика, 2000. ssp@ugrasu. ru 7

АКТУАЛЬНОСТЬ Многочисленные примеры успешного моделирования • Модели потребления • Модели производства • Модели экономического взаимодействия на простейших рынках • Модели управления запасами • Модели межотраслевого баланса • Модели прогнозирования • Модели оценки страховых рисков • Модели финансовых потоков • Инвестиционные модели • Модели коррупции • Модели системы образования И т. д. (Нобелевские премии по экономике – около 70%) ssp@ugrasu. ru 8

АКТУАЛЬНОСТЬ Учебные задачи тоже модели. Классические задачи: Задача оптимального раскроя материала Транспортная задача Задача о назначениях на работу Задача о смесях Задача о рюкзаке Задача о коммивояжере Задача о станках Задача о распределении капиталовложений Задача о размещении производства ssp@ugrasu. ru 9

Актуальность Привлекательность моделирования. • «Что будет, если…? » ; • «Как сделать, чтобы…. ? » . ssp@ugrasu. ru 10

ВВЕДЕНИЕ «Боязнь математики» Следует исходить не из сложности математики, а объективной необходимости математических знаний для современного экономиста и управленца. Рассмотрим некоторые примеры. ssp@ugrasu. ru 11

ВВЕДЕНИЕ Пример 1. Коммерсант приобретает некий товар по 7 руб. за штуку. Максимальный объем продаж y связан с назначаемой им ценой p по формуле y = 2940 − 140 p. Какое оптимальное количество товара должен приобрести коммерсант и какова должна быть оптимальная цена продажи товара? ssp@ugrasu. ru 12

ВВЕДЕНИЕ Пример 1. ssp@ugrasu. ru 13

ВВЕДЕНИЕ Пример 2. Пусть некоторый экономический регион производит несколько (n) видов продуктов исключительно своими силами и только для населения данного региона. Предполагается, что технологический процесс отработан, а спрос населения изучен. Надо принять решение о величине годового объема выпуска продуктов с учетом, что этот объем должен обеспечить как конечное, так и производственное потребление. ssp@ugrasu. ru 14

Пример 1 Составляем математическую модель. Обозначим известные величины: yi - спрос населения на i–й продукт aij - количество i-го продукта, необходимое для выпуска единицы j -го продукта по данной технологии (технологические коэффициенты). Обозначим неизвестные величины: xi - объем выпуска i-го продукта. ssp@ugrasu. ru 15

Пример 1 Классическая модель «затраты-выпуск» (модель В. Леонтьева). ssp@ugrasu. ru 16

ВВЕДЕНИЕ Т. о. математика – это инструментарий, экономика – объект приложения этого инструментария. Математика – «чистая» и прикладная. Добилась поразительных результатов в моделировании детерминированных процессов. Пример: полеты в космосе и возвращение обратно. Применение компьютеров. ssp@ugrasu. ru 17

ВВЕДЕНИЕ Бесспорные достоинства математики: • • единая система обозначений развитый аппарат безупречная логическая система заключений абстрагирование от предметной сущности процессов • универсальность методов. ssp@ugrasu. ru 18

ВВЕДЕНИЕ Для того чтобы воспользоваться всеми прелестями математики, необходимо формализовать экономические проблемы, создать математическую модель реального объекта ssp@ugrasu. ru 19

ТИПЫ МОДЕЛЕЙ Будем выделять три типа моделей: • Физические модели (макеты самолетов, городов…); • Аналоговые модели (карты местности, диаграммы…) • Математические модели Модель является абстракцией реальности, которая отражает преставления ее создателя о причинно-следственных связях в реальном мире ssp@ugrasu. ru 20

ВВЕДЕНИЕ Математическая модель реального объекта есть упрощенная, идеализированная, приближенная схема, составленная с помощью математических символов и операций, логических связей и графиков. ssp@ugrasu. ru 21

ВВЕДЕНИЕ Преимущества: • возможность эксперимента на модели, построение различных сценариев; • формализация позволяет рассматривать задачу как математическую и, следовательно, возможно применить всю мощь универсального математического аппарата; • оптимизация и прогнозирование ssp@ugrasu. ru 22

ВВЕДЕНИЕ Моделирование это творческий процесс, нет универсальных методов построения моделей. Однако общие принципы построения моделей, следующие: • адекватность; • объективность; • простота; • чувствительность; • устойчивость; • универсальность. ssp@ugrasu. ru 23

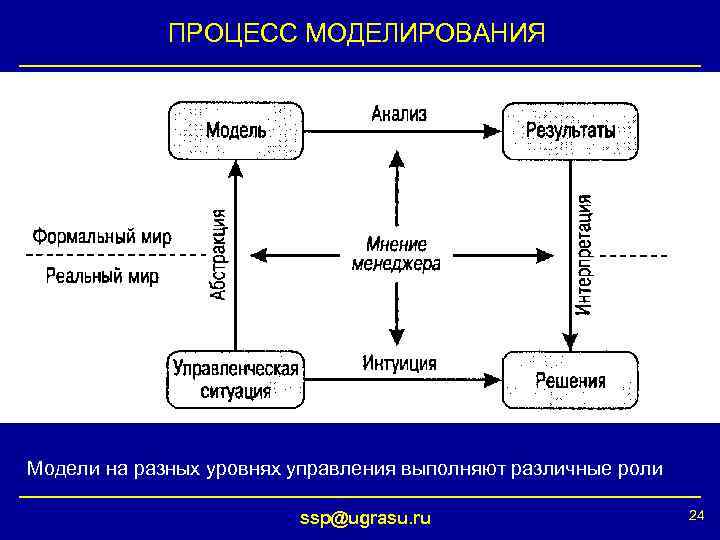ПРОЦЕСС МОДЕЛИРОВАНИЯ Модели на разных уровнях управления выполняют различные роли ssp@ugrasu. ru 24

ИНТУИЦИЯ И МОДЕЛИРОВАНИЕ Ни одна модель не в состоянии охватить реальность. То, что оптимально для модели, не всегда оптимально в жизни. Моделирование и интуиция не являются взаимоисключающими вещами. Интуиция управленца позволяет: • осознать проблему и определиться с направлением моделирования; • интерпретировать и реализовать решения. ssp@ugrasu. ru 25

ИНТУИЦИЯ И МОДЕЛИРОВАНИЕ Модель не решает проблемы, не предлагает готовые ответы, но поддерживает процесс принятия решения менеджером. Будет ошибкой слепо принимать решения на основании модели ( «так подсказал компьютер. . » ). Моделирование развивает интуицию! ssp@ugrasu. ru 26

ЭТАПЫ МОДЕЛИРОВАНИЯ Этапы системного анализа проблемы: 1. Предметный анализ проблемы 2. Формализация проблемы 3. Построение математической модели 4. Анализ модели с целью получения результатов 5. Интерпретация и проверка адекватности модели 6. Реализация результатов модели, применение для принятия решения в реальной ситуации ssp@ugrasu. ru 27

ЭТАПЫ МОДЕЛИРОВАНИЯ 1. Предметный анализ проблемы • изучение предметной области; • определение целей моделирования (как правило, одна); • формулировка проблемы; • выявление существенных аспектов и игнорирование второстепенных; • сбор данных (статистических, экспертных, результатов измерений и др. ) ssp@ugrasu. ru 28

ЭТАПЫ МОДЕЛИРОВАНИЯ 2. Формализация проблемы • предположения и упрощения; • набор факторов; • входы и выходы модели; • схема «черного» ящика» ; • на входе: контролируемые переменные (решения) и неконтролируемые (параметры); • на выходе: критерий эффективности и результирующие переменные. ssp@ugrasu. ru 29

ЭТАПЫ МОДЕЛИРОВАНИЯ 2. Формализация проблемы Примеры вопросов для управленца: • Прибыль – это решение или критерий эффективности? • Как отделить существенные переменные решения от второстепенных? Например, цена продукта, расходы на рекламу. • Действительно ли цена продукта является контролируемой величиной, или определяется конкуренцией на рынке? • Количество продуктов, которое нужно продать – это решение или результирующая переменная? • Дисциплина работников – критерий или параметр? Как измерять? • Доля рынка – критерий? Региональный, национальный или международный? В текущем году или за 5 -летку? В чем: в шт. товара или в деньгах? • Продажи конкурентов – параметр или результат? • Самостоятелен менеджер или исполняет волю руководства? • Что важнее: ежедневное, оперативное руководство или стратегическое планирование? • Интересы законодателей, потребителей, акционеров – параметры или критерии? ssp@ugrasu. ru 30

ЭТАПЫ МОДЕЛИРОВАНИЯ 3. Построение математической модели • Введение обозначений; • Выявление связей между элементами модели; • Составление уравнений (конечных, функциональных, дифференциальных и т. п. ) и иных соотношений между элементами модели; • Построение таблиц и графиков ssp@ugrasu. ru 31

ЭТАПЫ МОДЕЛИРОВАНИЯ 4. Анализ модели с целью получения результатов • Выбор вычислительного метода; • Построение алгоритма; • Программирование и отладка; • Проведение вычислений, получение решения; • Анализ чувствительности и устойчивости решения ssp@ugrasu. ru 32

ЭТАПЫ МОДЕЛИРОВАНИЯ 5. Интерпретация и проверка адекватности модели Соответствие здравому смыслу (? ) Проверка на тестовых данных Проблема в том, что в реальном мире бизнеса контролируемые эксперименты, как правило, невозможны. 6. Реализация результатов модели, применение для принятия решения в реальной ситуации ssp@ugrasu. ru 33

ЭТАПЫ МОДЕЛИРОВАНИЯ Как правило, этапы выполняются не строго последовательно, а итеративно. Результаты этапов критически анализируются, уточняются. ssp@ugrasu. ru 34

Пример построения модели Мур Дж. Х. , Уэдерфорд Л. Р. Экономическое моделирование в MICROSOFT EXCEL, 6 -е издание: пер. с англ. , 2004 г. , 1024 стр. Некто Самуэль Саймон решил создать свой бизнес. Сфера деятельности: изготовление яблочных пирогов, т. е. выпечка, упаковка, доставка. Предполагается оптовая реализация по бакалейным магазинам. Название: Simon Pie Производство уже идет, однако CC хочет построить модель своего бизнеса в Excel, чтобы изучить возможности расширения своей компании Воспользуемся рекомендациями. Рассмотрим по этапам. Параллельно работаем в Excel ssp@ugrasu. ru 35

Этап 1. Предметный анализ проблемы СС изучает технологию производства пирогов и ситуацию на оптовом рынке. Факторы, которые присутствуют в данном бизнесе: Прибыль, компоненты для производства пирогов, расходы на производство, хранение, материально-техническое обеспечение, аренда помещения, коммунальные платежи (газ, электричество, вода), транспортные расходы, выплаты процентов по кредиту и т. д. и т. п. Цель: максимизация прибыли В качестве критерия эффективности – недельная прибыль. Наиболее важное решение (контролируемая переменная) – оптовая цена. ssp@ugrasu. ru 36

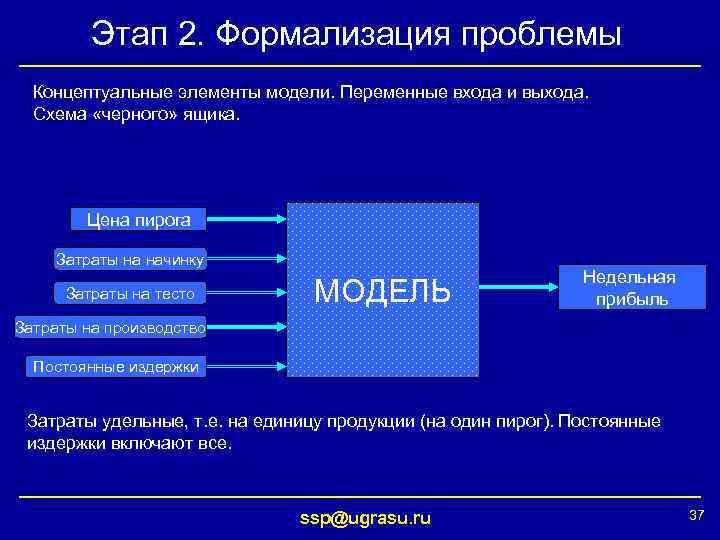Этап 2. Формализация проблемы Концептуальные элементы модели. Переменные входа и выхода. Схема «черного» ящика. Цена пирога Затраты на начинку Затраты на тесто МОДЕЛЬ Недельная прибыль Затраты на производство Постоянные издержки Затраты удельные, т. е. на единицу продукции (на один пирог). Постоянные издержки включают все. ssp@ugrasu. ru 37

Этап 3. Построение математической модели Разработка внутренней логики модели. Предварительно полезно построить диаграммы влияния Прибыль Доход Общие издержки Затраты на производство Спрос Цена на пирог Уд. затраты на производство Затраты на ингредиенты Количество ингредиентов Уд. затраты на начинку ssp@ugrasu. ru Уд. затраты на тесто Постоянные издержки 38

Этап 3. Построение математической модели Составляем уравнения: Прибыль = Доход – Общие затраты, Доход = Цена пирога х Спрос, Общие затраты = Затраты на обработку + Затраты на продукты + Постоянные издержки, Затраты на продукты = Кол-во начинки х уд. затраты на начинку + Кол-во теста х уд. затраты на тесто. ssp@ugrasu. ru 39

Этап 3. Построение математической модели Саймон уточняет значения входных переменных: Далее Саймон составляет электронные таблицы и изучает влияние входных параметров на значение недельной прибыли. ssp@ugrasu. ru 40

ВВЕДЕНИЕ Классификация моделей по признаку назначения: • Описательные • Модели принятия решения, включая оптимизационные (модели планирования) и игровые (задачи конфликтного характера), в отличии от первых содержат управляющие параметры. ssp@ugrasu. ru 41

ВВЕДЕНИЕ По степени агрегированности объектов моделирования: макроэкономические и микроэкономические модели; ssp@ugrasu. ru 42

КЛАССИФИКАЦИЯ МОДЕЛЕЙ Классификация моделей по признаку назначения: • Описательные • Модели принятия решения, включая оптимизационные (модели планирования) и игровые (задачи конфликтного характера). ssp@ugrasu. ru 43

КЛАССИФИКАЦИЯ МОДЕЛЕЙ По другим признакам: • Статические • Динамические Еще: • Детерминированные • Стохастические По бизнес-функциям: ssp@ugrasu. ru 44

ВВЕДЕНИЕ Классические задачи: (темы рефератов) Задача оптимального раскроя материала Транспортная задача Задача о назначениях на работу Задача о смесях Задача о рюкзаке Задача о коммивояжере Задача о станках Задача о распределении капиталовложений Задача о размещении производства ssp@ugrasu. ru 45

КЛАССИФИКАЦИЯ МОДЕЛЕЙ По типу математического аппарата, положенного в основу модели: • матричные модели; • модели линейного и нелинейного программирования; • регрессионные модели; • модели теории игр; • модели теории графов; • сетевые модели; • модели массового обслуживания; • модели управления запасами. ssp@ugrasu. ru 46

Пример 3. Нефтеперерабатывающий завод располагает двумя сортами нефти: сортом А в количестве 10 ед. и сортом В – 15 ед. При переработке из нефти получают; бензин (Б) и мазут (М). Имеется три варианта технологического процесса переработки: I. 1 ед. А+2 ед. В дает 3 ед. Б+2 ед. М II. 2 ед. А+1 ед. В дает 1 ед. Б+5 ед. М III. 2 ед. А+2 ед. В дает 1 ед. Б+2 ед. М Цена бензина – 10 долл. за 1 ед. , Цена мазута – 1 долл. за 1 ед. Требуется определить наиболее выгодное сочетание технологических процессов. ssp@ugrasu. ru 47

Пример 2 Составляем математическую модель. Уточним, что значит выгодно? Получение максимальной прибыли. Для этого следует определить, какую технологию и сколько раз применить. Возможных вариантов достаточно много. ssp@ugrasu. ru 48

Пример 2 Xi- количество вариантов использования i –го технологического процесса ssp@ugrasu. ru 49

Пример 2 ssp@ugrasu. ru 50

Пример 2 Задача линейного программирования. Пример оптимизационной модели детерминированного типа. ssp@ugrasu. ru 51

Пример 3 Контрольные вопросы: 1. Понятие о математической модели. Примеры. 2. Общие принципы построения моделей 3. Этапы системного анализа проблемы 4. Шаги построение математической модели 5. Классификация математических моделей 6. Пример 1. Модель «затраты-выпуск» 7. Пример 2. Наиболее выгодное сочетание технологических процессов нефтеперерабатывающего завода ssp@ugrasu. ru 52