8Языки реляционных баз данных.ppt
- Количество слайдов: 52

Языки реляционных баз данных Бессарабов Н. В. bes@fpm. kubsu. ru 2010 г. 1

Цели лекции Начинаем рассматривать языки используемые в базах данных. Фактически один из них уже построен. Это язык реляционной алгебры. Сравним математический подход к языкам как моделям структур и алгоритмов с представлениями лингвистов о языках вообще. Это даст нам утверждение об ограниченности любых языков, формулируемое как гипотеза Сепира-Уорфа. Затем рассмотрим понятие исчисления и для нужд реляционной модели данных сформулируем два исчисления: на кортежах и на доменах. Особая роль реляционной алгебры в том, что она служит эталоном для языков, работающих с реляционными данными. Способность языка моделировать реляционную алгебру называется реляционной полнотой. Для полноценного усвоения материала лекции необходимо решать достаточное количество примеров. Win. RDBI позволит вам поработать с реляционной алгеброй, исчислениями на кортежах и доменах и версией 2 1 языка SQL, позволяющей формулировать только запросы.

1. Тезис Чёрча и гипотеза Сепира-Уорфа 3

Тезис Чёрча Формулировка тезиса Чёрча: “Интуитивное понятие эффективной вычислимости корректно эксплицируется понятием вычислимости по Тьюрингу” Замечание: Попытки формализовать понятие вычислимости привели к созданию λ-исчисления, лежащего в основе функционального программирования (типичный представитель -- язык LISP). Ошибка некритического мышления, принимаемая за следствие тезиса Чёрча: В любом языке программирования можно и нужно решать любые задачи. Такой подход, как минимум, чрезмерно усложняет программные тексты и затрудняет восприятие их человеком. 4

Гипотеза лингвистической относительности Сепира-Уорфа “Мы выделяем в мире явлений те или иные категории и типы совсем не потому, что они (категории и типы) самоочевидны; напротив, мир предстает перед нами как калейдоскопический поток впечатлений, который должен быть организован нашим сознанием, а это значит – в основном языковой системой, хранящейся в нашем сознании…Мы сталкиваемся, таким образом, с новым принципом относительности, который гласит, что сходные физические явления позволяют создать сходную картину вселенной только при сходстве или, по крайней мере, при соотносительности языковых систем” [Уорф]. 5

Искусственные языки (1/2) Искусственные языки (ИЯ) существенно отличаются от естественных (ЕЯ) по происхождению и вмещающей среде, зачастую предполагающей в качестве носителей языка кроме человека ещё и компьютер. Из всех функций ЕЯ в ИЯ в полной мере развита только коммуникативная. Не нужна, естественно, экспрессивная функция. Недостаточно развита аккумулятивная функция, обеспечивающая сохранение опыта и знаний. Почти не используется конструктивная функция, которую в контексте ИЯ можно рассматривать как функцию формирования знаний. В ИЯ выделим две категории, не предполагая дихотомического их разделения: • Языки программирования и моделирования программ. • Диаграммные языки визуализации знаний и рассуждений. Таким образом, к вербальным языкам программирования присоединяются диаграммные языки вроде UML, языки 6 спецификаций и описания программ, пакетов и плагинов.

Искусственные языки (2/2) • • Основные особенности ИЯ, отличающие их от ЕЯ: ИЯ конструируются эксплицитно, а не складываются в процессах деятельности и общения; ИЯ оторваны от человеческого мышления и потому лишены способности получать информацию, не имеющую заранее подготовленного шаблона, не могут соотносить её с уже имеющейся информацией, то есть, не поддерживают метафорическое мышление; носители ИЯ, качественно неоднородны (человек «с улицы» , человек специалист предметной области, человек программист, машина с определенным программным обеспечением и т. д. ); обилие невербальных языков и невербальных компонентов ИЯ; широкое использование встраивания одного языка в другой (серверные страницы, встроенный SQL), создания языков с вербальной и невербальной компонентой (например, QBE), и т. д. ; одновременное использование нескольких языков при работе с несколькими моделями данных или видами деятельности; ограничения на графические языки, вызванные особенностями восприятия и распознавания человеком; быстрое развитие ИЯ, наметившееся сужение областей применения новых языков (в DSL, MDA и т. п. ), а значит и числа «носителей» языка. 7

Когнитивное направление в науке и искусственные языки Когнитивизм – это направление в гуманитарной науке, изучающее знание и познание, восприятие мира в процессе деятельности людей, причём “… исследуются не просто наблюдаемые действия, а их ментальные репрезентации (внутреннее представление модели), символы, стратегии человека, которые и порождают действия на основе знаний”. Когнитивная лингвистика рассматривает лишь ту часть информации, которая отражается в языке. 8

2. О языках информационных систем 9
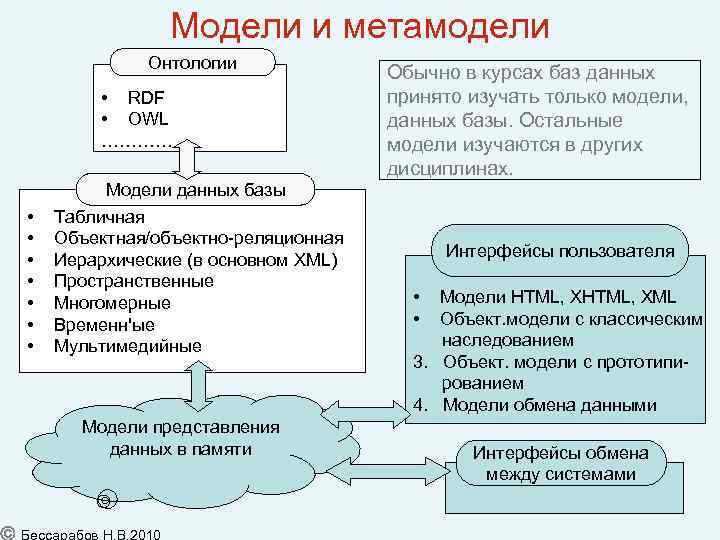
Модели и метамодели Онтологии • RDF • OWL ………… • • Модели данных базы Табличная Объектная/объектно-реляционная Иерархические (в основном XML) Пространственные Многомерные Временн'ые Мультимедийные Модели представления данных в памяти Обычно в курсах баз данных принято изучать только модели, данных базы. Остальные модели изучаются в других дисциплинах. Интерфейсы пользователя • Модели HTML, XML • Объект. модели с классическим наследованием 3. Объект. модели с прототипи рованием 4. Модели обмена данными Интерфейсы обмена между системами 10

Сколько языков программирования нужно знать для работы с ИС? Пример Oracle. Сейчас и 20 лет назад. 1995 год 1. 2. 3. 4. 5. 6. SQL PL/SQL SQL*Plus C++ HTML Java. Script Сейчас 1. 2. 3. 4. 5. 6. SQL PL/SQL SQL*Plus C++ HTML Java. Script 7. Язык Java + технологии 8. XML (XSL, XPath, Schema, RELAX NG, XQuery, XMI) 9. Ruby (+ Rails) 10. Языки для представления семантики (RDF, OWL, …) 11. Языки, специфичные для предметной области (DSL, MDA) 11

Сочетание двух языков В серверных страницах (ASP, JSP, CSP) в текст на одном языке, например HTML, можно вставлять скриптлеты – тексты на другом языке. Пример: JSP (Java Server Pages). Вмещающий текст на HTML, а вставки (выражения, скриптлеты, объявления) на Java. Выражение вставляет вычисляемое значение Текст серверной <HTML> непосредственно в формистраницы <HEAD> руемую HTML-страницу. <TITLE> Пример JSP </TITLE> Скриптлет даёт часть кода для </HEAD> формируемого метода сервер<BODY> <H 2> Выражение и скриплет JSP </H 2> ной страницы. <UL> <LI> Дата и время: <%= new java. util. Date() %> <LI> Выражение <% Date h. Date = new java. util. Date(); out. println("Дата и время: "+h. Date); %> Вид в окне браузера </UL> Выражение и скриплет JSP Скриптлет </BODY> • Дата и время: Sun Dec 05 22: 37: 32 MSK 2004 12 </HTML> • Дата и время: Sun Dec 05 22: 37: 32 MSK 2004

3. Языки основанные на исчислениях 13

Ограниченность языка реляционной алгебры Перечислим некоторые типы запросов, не выразимых средствами реляционной алгебры: 1. запросы, требующие дать в ответе список отношений и/или атрибутов, удовлетворяющих определенным условиям (например, “в каких отношениях имеется атрибут sal? ”); 2. запросы, требующие построения транзитивного замыкания отношений. Запросы первого типа требуют использования языков, основанных на логике предикатов второго порядка, у которых кванторы могут навешиваться не только на переменные, как у языков первого порядка, но и на имена предикатов. Типичный пример запроса второго типа рассмотрен на следующих слайдах. Станет понятно, что для записи такого запроса язык должен представлять рекурсию. 14
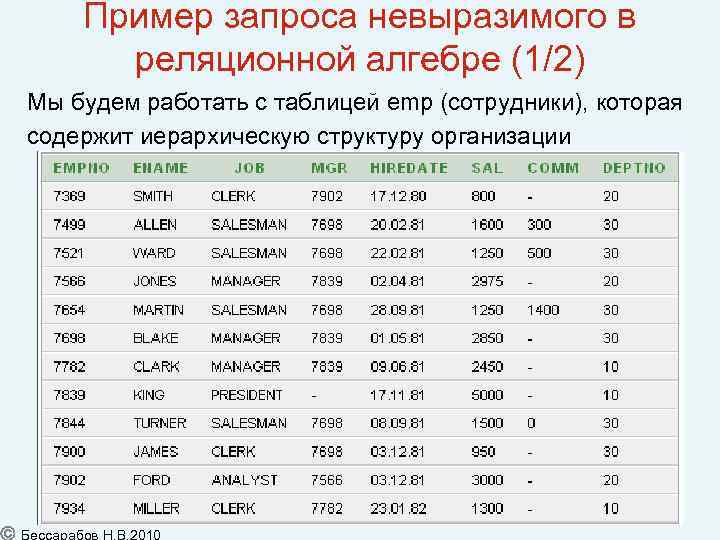
Пример запроса невыразимого в реляционной алгебре (1/2) Мы будем работать с таблицей emp (сотрудники), которая содержит иерархическую структуру организации 15

Пример запроса невыразимого в реляционной алгебре (2/2) Отследим цепочку начальников Smith’а. Его непосредственный начальник имеет табельный номер 7902. Это аналитик Форд. Его начальник с табельным номером 7566 менеджер Jones, а у того начальник президент King с табельным номером 7839. Так вот, для поиска непосредственных начальников каждого сотрудника достаточно написать простой запрос: proj {E 1. ENAME=E 2. ENAME} (join E 1. MGR=E 2. EMPNO (EMP E 1, EMP E 2)) Запись вида EMP E 1 означает переименование EMP в E 1. Найти всех начальников невозможно, так как для поиска каждого следующего начальника придется сделать ещё одно соединение, а длина цепочки начальников различна для разных сотрудников и, вообще говоря, не может быть определена заранее. Чтобы рекурсия была возможна, язык запросов должен был позволить повторение соединения каждого построенного отношения с исходным до тех пор, пока не найдётся сотрудник не имеющий начальника. Замечание: В 3 -й версии языка SQL рекурсивные запросы возможны. 16

Языки запросов, основанные на логических исчислениях Реляционная алгебра определяет набор операций, комбинируя которые можно создать отношение, обладающее нужными свойствами. Полученное отношение это и есть ответ на запрос. Существует ещё три в некотором смысле эквивалентных подхода к построению систем запросов – реляционные исчисления на кортежах, на доменах и, так называемые, табло. Знания только реляционной алгебры даже для практики недостаточно, потому что два наиболее известных языка для работы с реляционными базами данных -- SQL (Structured Query Language) и QBE (Query by Example) -- основаны, соответственно, на реляционных исчислениях на кортежах и на доменах. В настоящее время языками основанными на реляционной алгебре не пользуются. А зачем же мы её изучаем? Удобство исчислений в том, что в запросах формируются условия, которым должен удовлетворять результат запроса. По ним и отбираются строки. В сложных запросах реляционной алгебры последовательно получаются промежуточные отношения. В реализациях это замедляет 17 получение ответа.

Роль языка реляционной алгебры Язык реляционной алгебры служит своеобразным эталоном для языков запросов к реляционной базе данных. Определение: Язык запросов к базе данных, способный моделировать реляционную алгебру, обладает свойством реляционной полноты. Займёмся исчислениями. Изложение по недостатку места и времени будет отрывочным, но достаточным для практического освоения исчислений на кортежах и доменах. На их основе будут изучены два основных языка для работы с базами данных -- SQL и QBE. 18

Логические исчисления Определение: Исчисление это “дедуктивная система, т. е. способ задания множества путем указания исходных элементов (аксиом исчисления) и правил вывода, каждое из которых описывает, как строить новые элементы из исходных и уже построенных. Выводом в исчислении называется такое линейно упорядоченное множество, что всякий его элемент P является либо аксиомой исчисления , либо заключением применения какого-либо принадлежащего правила вывода, причем все посылки этого применения предшествуют P в выводе. ” [1] Исчисление высказываний изучает логические связи между высказываниями, рассматриваемыми как единое целое, без учета их строения. Исчисление предикатов формализует логику, изучающую субъектно-предикатную структуру высказываний. Иcчисление предикатов охватывает свойства (одноместные предикаты) и отношения (многоместные предикаты). Исчисление высказываний это исчисление нульместных предикатов. 19

Алгебра множеств и логика В школьной математике принято иллюстрировать операции над множествами на примере линейно упорядоченных множеств. Вычисления проводятся фактически для интервальных множеств и потому стирается разница в вычислительном аспекте операций над множествами и эквивалентных операций над соответствующими предикатами. Следует помнить, что отношения это не упорядоченные множества кортежей и потому вычисление предикатов может быть существенно эффективнее действий над множествами кортежей. Дело в том, что в запросах в алгебре необходимо построить как результат каждой операции своё промежуточное отношение. В исчислении могут проверяться сложные условия, выраженные предикатами и строится единственное результирующее отношение. 20

Предикаты Исчисление высказываний не позволяет оперировать с обобщенными утверждениями, содержащими переменные. Этот недостаток устраняется использованием предикатов. Определение: Предикат Р(Х 1…Хn) это утверждение P об объектах Х 1…Хn. Сами объекты Х 1…Хn могут рассматриваться как переменные. Примеры: • высказывание “погода(вторник, дождь)” • предикат “погода(D, W )” Здесь “погода” предикатный символ (предикат), D и W переменные, а “вторник”, “дождь” константы. Одноместные предикаты обозначают свойства (например, "быть человеком "), предикаты двухместные и с бóльшей арностью обозначают отношения и операции, 21 например, двухместный предикат "выше, чем".

Кванторы Особый интерес представляют предикаты, значение истинности которых определяются на некотором наборе переменных. Широко используются: • квантор всеобщности – «для всех» и • квантор существования – читается «существует» . Реже употребляется • сильный квантор существования ! – «существует единственный» . Примеры: • Х Х+1>Х • Х Х/2=4 • !Х Х/2=4 Переменная, на которую навешен квантор, называется связанной. Например, в формулах Х (X=Y) и Х B(X, Y) переменная X связана, а Y свободна. 22

Понятие исчисления Определение 1: Исчислением или формальной теорией называют систему правил оперирования со знаками, используемую для доказательства или опровержения предложений, выразимых с помощью допустимого набора знаков. Определение 2: Исчисление состоит из: • набора символов образующих алфавит; • набора правильно построенных формул -- ППФ (well-formed formulas -- WFF); • выделенного подмножества правильно построенных формул, называемых аксиомами; • правил вывода, определяющих способ получения формул из других формул. Иногда систему аксиом строят исходя из некоторой схемы. Выделяют логические аксиомы, определяющие базовую логику. Специфика теории может потребовать добавления нелогических аксиом. Мы будем рассматривать исчисления с конечным алфавитом, конечным числом аксиом и формулами конечной длины. 23

Правила вывода Используются, в частности, следующие правила вывода • правило modus ponens (правило отделения): Если A B истинны, то выводимо B. • правило modus tollens: Если A B истинно, и B ложно, то выводимо A. Определение: Формальное доказательство формулы А в исчислении это построение конечной последовательности формул А 1…Аn, причем, А= Аn. Каждая из формул Аi этой цепочки либо аксиома, либо получена из других формул с помощью правил вывода. А называется теоремой. С помощью символа «доказуемо» ├ запишем этот факт как ├А. Вспомним, что высказывание в логике предикатов это формула, все переменные которой связаны кванторами. 24

Свойства исчисления Определяющими свойствами любого исчисления являются полнота и непротиворечивость. Определение (полнота): Формальная теория называется полной, если для любого высказывания А логики предикатов или ├А или ├ А. Определение (непротиворечивость): Формальная теория называется непротиворечивой, если формула А А в ней недоказуема для произвольного высказывания А теории. Замечание: Как показал К. Гёдель в своей знаменитой теореме доказательство непротиворечивости невозможно выполнить даже в рамках формальных теорий для простых математических объектов. 25

Исчисление высказываний Определение 1: Высказывание это утверждение которое имеет однозначно определенное значение истинности. Определение 2: Символы исчисления это символы высказываний A, B, C, …, символы значений истинности T, и символы логических связок V, , , . Определение 3: Правильно построенные формулы (ППФ) • Символ высказывания или значения истинности это ППФ; • Отрицание ППФ есть ППФ; • Конъюнкция и дизъюнкция ППФ есть ППФ; • Импликация одной ППФ в другую ППФ есть ППФ; Системы аксиом исчисления высказываний (например, аксиоматика Клини) известны, но мы их не рассматриваем, так как мы не будем строить доказательства исходя из выбранной системы аксиом. 26

ППФ в исчислении предикатов Логика высказываний расширяется до логики предикатов путём включения в формулы утверждений, являющихся предикатами. Естественно, включаются и предикатные переменные. Поэтому определение ППФ усложняется. Определение терма: • Переменные Х 1…Хn и константы C 1…Cm– это термы; • Если f(∙, …, ∙) функция n-переменных, ставящая в соответствие изучаемым объектам другой объект, и t 1…tk термы, то f(t 1…tk) терм; Определение формулы: • Если Р(∙, …, ∙) n-местный предикат, а t 1…tn термы, то P(t 1…tn ) (атомарная) формула; • Если А и В формулы, то (А В), (АVВ), (А В) формулы; • Если А формула, то А формула; • Если А(Х) формула, содержащая переменную Х, то ХА(Х), ХА(Х) формулы. 27

Замечание о функциональных символах При внимательном прочтении определения терма, приведённого на предыдущем слайде должны возникнуть вопросы: 1. Чем функциональный символ отличается от предикатного символа? 2. А зачем вообще нужны функциональные символы? Ответ на первый вопрос: n-местный предикат на множестве M задаёт отображение Mn {T, }, а n-местная функция определяет отображение Mn M. Ответ на второй вопрос: 0 -местная функция M 0 M отождествляется с элементом множества M. Не всегда удобно иметь отдельный символ для каждого элемента множества M. Функциональные символы позволяют дать более сжатое представление. Например фраза естественного языка “моя левая нога” может пониматься как существование левой ноги у субъекта “Я” и записываться как функция “Левая. Нога(Я)”, что позволяет не именовать левые ноги всех людей. Важно понимать, что за определённой таким образом функцией не предполагается никакой процедуры её вычисления. 28

Определение узкого исчисления предикатов Для определения узкого исчисления предикатов необходимо определить набор допустимых символов, правильно построенные формулы, набор аксиом и правила вывода. Полезно сравнить определение предыдущего слайда с определением исчисления высказываний на слайде 26. Определение 1: Предикат Р(Х 1…Хn) это утверждение P об объектах Х 1…Хn. Определение 2: Символы исчисления предикатов это символы переменных, констант, функций и предикатов, символы значений истинности T, , символы логических связок V, , , и кванторы общности и существования . 29

Определение узкого исчисления предикатов (продолжение) • Правильно построенные формулы и входящие в них термы определены выше на слайде 27. • Набор аксиом включает аксиомы исчисления высказываний (упоминаются на слайде 26) и следующие дополнительные аксиомы: x A(x) A(t) x A(x) где t=t(x 1, . . xn) терм и в формуле A нет кванторов xi, (i=1, …n) • Дополнительные правила вывода: Если B A(x), то B x A(x). 30 Если A(x) B, то x A(x) B.

Дополнительные правила вывода Это “исключение ”, “введение ” и “универсальное инстанцирование”. Определение 1: “Исключение ” это вывод истинности обоих конъюнктов A и B из истинности A B. Определение 2: “Введение ” это вывод истинности A B из истинности обоих конъюнктов A и B. Определение 3: (Правило универсального инстанцирования): Если любую переменную, стоящую под квантором всеобщности заменить на любой терм из области определения, то полученное выражение истинно. Например, если терм A принадлежит той же области определения, что X, и X P(X), то выводимо P(A). 31

Порядок исчисления предикатов Исчисление первого порядка: В исчислении первого порядка можно связывать знаком квантора только переменные, но не функции или предикаты. Исчисление высших порядков: В исчислении предикатов высших порядков можно связывать знаком квантора не только переменные, но и функции и предикаты. Прикладное исчисление предикатов: В такое исчисление введены дополнительные знаки констант, функций, операций, предикатов, дополнительные аксиомы, связывающие эти новые знаки. Пример: Исчисление предикатов с равенством. 32

Реляционное исчисление предикатов на кортежах (TRC) В реляционном исчислении на кортежах ( Tuple Relation Calculus -- TRC) правильные формулы строятся как описания условий, которым должны удовлетворять кортежи образующие искомые отношения. Эти условия в простейшем варианте имеют вид: {t|P(t)} Здесь t - переменная, обозначающая некоторый кортеж, а P - предикат от этой переменной. Формула исчисления кортежей описывает множество всех таких кортежей, для которых предикат принимает значение “истина”. Общий вид правильно построенных формул исчисления на кортежах приведен ниже в разделе “Синтаксис запросов TRC в Win. RDBI”. 33

Состав предиката P(t) в исчислении на кортежах(1/2) Элементарными образующими предиката P(t) являются атомы следующих трёх видов: 1. Переменные кортежи t r, где r - отношение. Данный атом имеет значение истина, если кортеж t принадлежит отношению r. При этом если отношение имеет схему R , то и кортеж t имеет такую же схему. Пример: Пусть отношение СОТРУДНИК имеет схему {ИМЯ, ФАМИЛИЯ, ОТЧЕСТВО, ВОЗРАСТ}. Утверждение t СОТРУДНИК, означает, что t является кортежем отношения СОТРУДНИК, и имеет ту же схему {ИМЯ, ФАМИЛИЯ, ОТЧЕСТВО, ВОЗРАСТ}. 34

Состав предиката P(t) в исчислении на кортежах(2/2) 2. Отношения между кортежами s. A θ t. B, где s и t - некоторые кортежи, A и B - имена атрибутов, причем A S и B R, и θ - оператор сравнения (<, =, … ). Этот атом принимает значение истина, тогда и только тогда, когда атрибут A кортежа s находится в отношении θ с атрибутом B кортежа t. Например, если s, t СОТРУДНИК, то s. ВОЗРАСТ < t. ВОЗРАСТ истинно, если возраст сотрудника s меньше возраста сотрудника t. 3. Отношения между кортежем и константой s. A θ c, где s - некоторый кортеж, A - имя атрибута ( A S), а c – константа из домена атрибута A. Атом принимает значение ''истина'', если значение атрибута A кортежа s находится в отношении θ с константой c. Например, s. ВОЗРАСТ<40 истинно, если возраст сотрудника s меньше 40. 35

Правильно построенные формулы исчисления на кортежах Могут использоваться логические операции, кванторы и скобки. Рекурсивное определение правильно построенных формул: 1. Атом это ППФ. 2. Если P и Q ППФ, то P V Q, P Q, P будут ППФ. 3. Если P ППФ, то Х P(X) ППФ. 4. Если P ППФ, то Х P(X) ППФ. 5. Если P ППФ, то (P) ППФ. 6. Ничто иное не является ППФ. Замечание: Квантор существования обычно обозначается как EXISTS, квантор всеобщности как FORALL. 36

Сопоставление операторов реляционной алгебры и формул исчисления на кортежах 1. Объединение R U S = {t| t R V t S} 2. Разность R-S = {t| (t R) ( t S} 3. Селекция sel F (R) = {t|t R F} 37

О реляционной полноте языка запросов Как определено ранее, язык запросов к реляционной базе данных называется реляционно полным, если он по крайней мере так же выразителен, как язык запросов реляционной алгебры. Иначе говоря, реляционно полный язык позволяет, по крайней мере, моделировать язык запросов реляционной алгебры. Используемые в практике языки запросов “более чем полны” за счет: • включения арифметики и вычисления однострочных функций; • включения агрегатных (многострочных) функций; • иногда за счет вычисления транзитивного замыкания отношения. 38

Синтаксис запросов TRC в Win. RDBI Запрос (ППФ) имеет вид: { t 1, …, tn | F (t 1, …, tn ) }, где • F – формула исчисления; Пусть F, F 1, F 2 формулы • t 1, …, tn -- кортежные Тогда формулами будут: переменные, действующие как ( F ) not F глобальные переменные в F и определяющие схему результата F 1 and F 2 Обозначим: t и ti переменные кортежи aj атрибут c константа уровня домена оператор сравнения Тогда атомами будут: r(t), ti. am tj. an , t. ai c F 1 or F 2 Если t свободна* в F(t), то формулами будут (exists t) F(t) (forall t) F(t) ------------------*) Переменная свободна в формуле, если она не квантифицирована действием exists или forall 39

Реляционная полнота реляционного исчисления на кортежах Как вы помните, для доказательства достаточно выразить операции реляционной алгебры через операции исследуемой системы. Итак, исчисление первого порядка на кортежах реляционно полно. 40

Реляционное исчисление на доменах (1/3) В реляционном исчислении на доменах (Domain Relational Calculus -- DRC) область определения переменных не набор кортежей отношения, а домены. Отношение состоит из кортежей, в которые входят значения, принадлежащие доменам. Поэтому необходимо как-то показывать, что некоторые значения на доменах входят в один кортеж. С этой целью в исчисление на доменах (в отличие от исчисления на кортежах) вводится дополнительный набор предикатов, выражающих условия принадлежности. Пусть r – это n-арное отношение с атрибутами A 1, A 2, . . . , An. Тогда условие принадлежности можно записать так: r (Ai 1 : Vi 1, Ai 2 : Vi 2, . . . , Aim : Vim), где Vij – это либо константа, либо имя доменной переменной. 41

Реляционное исчисление на доменах (2/3) Условие принадлежности истинно тогда и только тогда, когда в отношении r существует кортеж, содержащий заданные значения Vij указанных j-тых атрибутов кортежа i, то есть Aij. Если Vij – константа, то условие на атрибут Aij зависит от текущих значений доменных переменных; если же Vij – имя доменной переменной, то условие принадлежности может принимать разные значения истинности при разных значениях этой переменной. 42

Реляционное исчисление на доменах (3/3) Во всех остальных отношениях правильно построенные формулы и выражения исчисления доменов и исчисления кортежей аналогичны. В частности, формулы могут включать кванторы, и различаются свободные и связанные вхождения доменных переменных. Сравните форму записи запроса в исчислении на доменах { d 1, …, dn | F (d 1, …, dn ) } и аналогичную форму для исчисления на кортежах { t 1, …, tn | F (t 1, …, tn ) } (см. слайд 39 и следующий слайд 44). 43

Синтаксис запросов DRC в Win. RDBI Запрос имеет вид: { d 1, …, dn | F (d 1, …, dn ) }, где • F – формула исчисления; • d 1, …, dn – доменные переменные, действующие как глобальные переменные в F и определяющие схему результата. Результатом запроса DRC будет Пусть F, F 1, F 2 формулы множество всех кортежей d 1, …, dn Тогда формулами будут: таких, что подстановка di в di ( F ) not F делает формулу F истинной. F 1 and F 2 F 1 or F 2 Обозначим: Если d свободна* в F(d), di переменная-домен формулами будут c константа уровня домена (exists d) F(d) оператор сравнения (forall d) F(d) Тогда атомами будут: ------------------r(d 1, d 2, …, dn) *) Свободная переменная не di dj квантифицирована действием di c 44 exists или forall

Реляционная полнота реляционного исчисления на доменах Итак, исчисление первого порядка на доменах реляционно полно. Замечание 1: Условия вида R(r 1, …, rn) это условия принадлежности Замечание 2: Сравните со слайдом 31. 45

Запросы, основанные на реляционной алгебре и на исчислениях Основное отличие языков, основанных на реляционной алгебре и на исчислениях в уровне процедурности. Запросы основанные на реляционной алгебре задают дерево алгебраических операций, то есть имеют однозначную процедурную интерпретацию (с учетом старшинства операций и расстановки скобок). Запрос реляционного исчисления не имеет однозначной процедурной интерпретации. Он только устанавливает условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются менее процедурными и, соответственно, более декларативными. Замечание: Из полноты исчислений на кортежах и доменах следует, что любой реляционно полный язык позволяет не только моделировать язык запросов реляционной алгебры, но и языки запросов реляционных исчислений на кортежах или на доменах. 46

Заключение Итак, на довольно примитивном, но достаточном для наших целей уровне, изучены: • исчисления вообще; • исчисления на кортежах и доменах. На практических занятиях в Win. RDBI вы должны были обнаружить, как много важных особенностей запросов не могут быть выражены в изученных исчислениях. Остаётся сделать почти очевидный вывод о необходимости расширения языков. Вопрос в том, как это сделать, какие расширения обеспечат языку жизнеспособность, можно ли как то расширить базисную теорию и на её основе развивать язык? В оставшейся части курса мы не ставим задачу указать пути расширения теории. Мы просто рассмотрим версии языков SQL и QBE, основанных, соответственно, на исчислениях на кортежах и доменах, но существенно пополненных средствами, выходящими за рамки этих исчислений, и увидим как растёт мощность языка. Что же касается способов расширения языков, укажем только, что вариант с расширением базисной теории не перспективен. 47

Литература 1. Исчисление. Математическая энциклопедия. Т. 2. М. : Изд-во “Советская энциклопедия”. С. 684 48
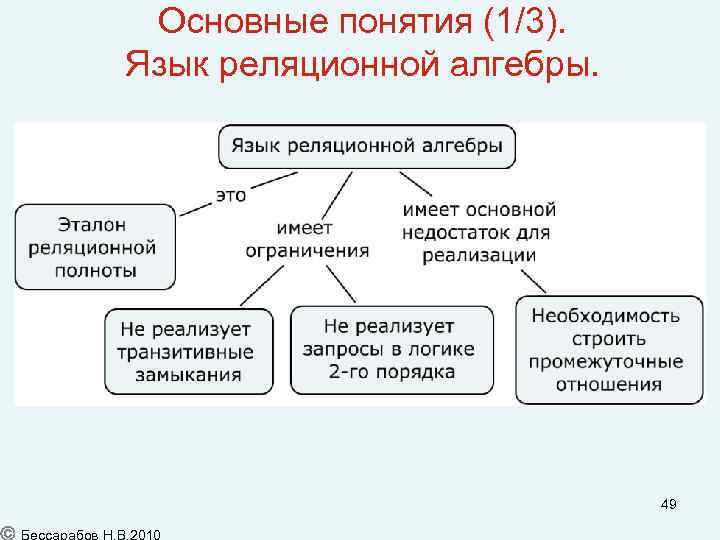
Основные понятия (1/3). Язык реляционной алгебры. 49
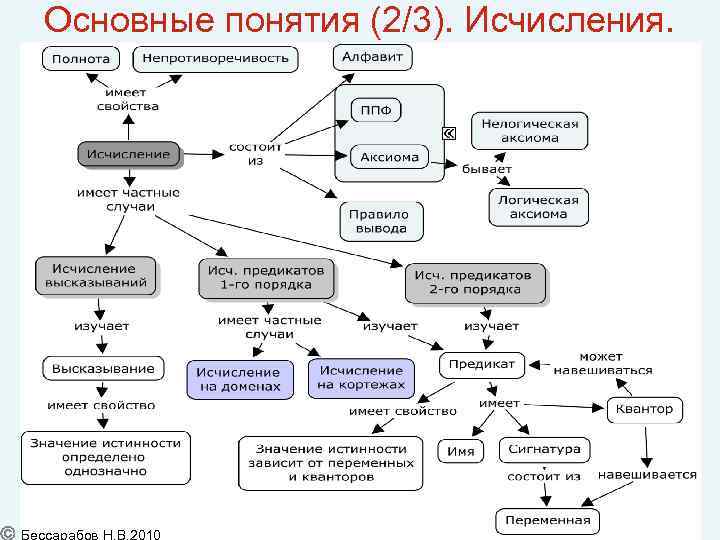
Основные понятия (2/3). Исчисления. 50
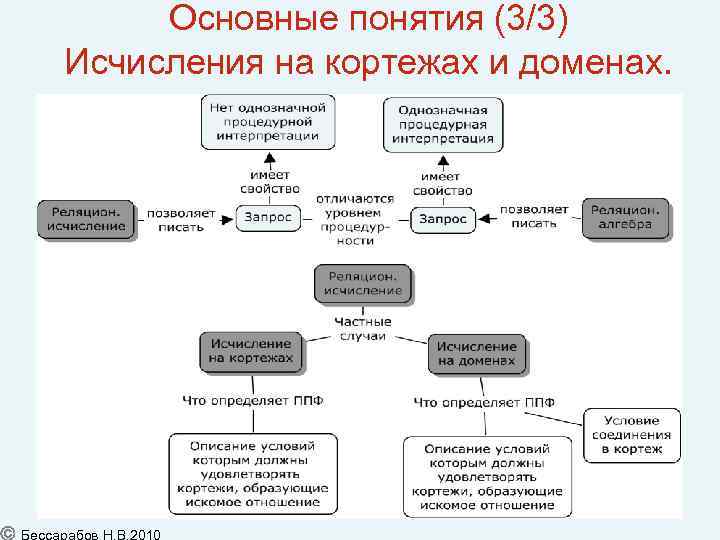
Основные понятия (3/3) Исчисления на кортежах и доменах. 51

Словарь студента Исчисление это “дедуктивная система, т. е. способ задания множества путем указания исходных элементов (аксиом исчисления) и правил вывода, каждое из которых описывает, как строить новые элементы из исходных и уже построенных. Выводом в исчислении называется такое линейно упорядоченное множество, что всякий его элемент P является либо аксиомой исчисления , либо заключением применения какого-либо принадлежащего правила вывода, причем все посылки этого применения предшествуют P в выводе. ” [1] 52
8Языки реляционных баз данных.ppt