Якушева Галина Михайловна Учитель математики ГОУ СОШ с

Якушева Галина Михайловна Учитель математики ГОУ СОШ с углубленным изучением английского языка № 1279 Юго-западного окружного управления образования Департамента образования города Москвы

Образование • Закончила математический факультет Московского государственного педагогического института имени В. И. Ленина • Первый московский целевой выпуск

Категория и стаж работы • • Учитель математики – 27 лет Высшая категория -15 лет Учитель методист - 20 лет Почетный работник общего образования РФ • Почетный работник города Москвы

Мои школы • № 254, г. Москва – 1 год • № 626, г. Москва – 5 лет • № 1279 (№ 26), г. Москва – 21 год и работаю по настоящее время

Мои медалисты • 87 медалистов, из них: § 34 золотых § 53 серебряных § В 2003 году первых профильных выпуск 18 медалистов

Мои книги

Участие в конференциях ü ü ü ü Международная конференция «Образование глазами детей и взрослых в 21 веке» по теме « Проблемность и межпредметность в образовании – условия устойчивого развития цивилизации» , март 2004 года. Международная конференция «Образование глазами детей и взрослых в 21 веке» по теме «Проблемы образования в условиях устойчивого развития цивилизации» , март 2005 года Международная конференция «Образование глазами детей и взрослых в 21 веке» по теме «Проблемность и профильность – условия устойчивого развития цивилизации» , март 2006 года Ежегодные конференции, посвященные профильному образованию и взаимодействие высших учебных заведений и школ в Академии труда и социальных отношений. 2004 -2007 года. Конференция «Новые образовательные технологии в образовательном процессе» , ВВЦ, апрель 2006 года Окружной круглый стол «Профильное обучение, перспективы развития» , выступление с презентацией, сентябрь 2006 года Установочная конференция учителей математики, участвующих в городском проекте «Школа информатизации» , декабрь 2006 года.

Технологии • Технология уровневой дифференциации обучения на основе обязательных результатов. • Проблемное обучение. • Технология перспективно-опережающего обучения с использованием опорных схем. • Технология метода проектов. • Технология индивидуальной образовательной траектории. • Информационно-компьютерные технологии. В прошлом учебном году начала участвовать в проекте «Школа информатизации» и освоила новую версию информационно-компьютерной технологии «Живая математика» .

Школа будущего – Школа информатизации • Городской проект «Школа информатизации» – 1 этап начальный курс «Живой математики» . – 2 этап базовый курс «Живой математики» . – 3 этап семинар-практикум по «Живой математике» . Создание мультимедиа пособий к урокам.

Темы самообразования • Технология проблемного обучения при изучении математики на старшей ступени обучения • Организация элективных курсов по математике в профильных классах • Организация элективных курсов по математике в предпрофильных классах. Диагностика профильного обучения.

Профильные выпуски • 10 выпусков, из них: § § § 2 физико-математических класса 3 социально-экономических класса 1 гуманитарный класс 1 лингвистический класс 1 лицейский класс

Мои классы • 9 а класс– предпрофильный социальноэкономический • 10 а класс – социально-экономический • 11 а класс – социально-экономический

ДИАГНОСТИКА ПРОФИЛЬНОГО ОБУЧЕНИЯ Составлена на основе анкет учащихся, их родителей и учителей

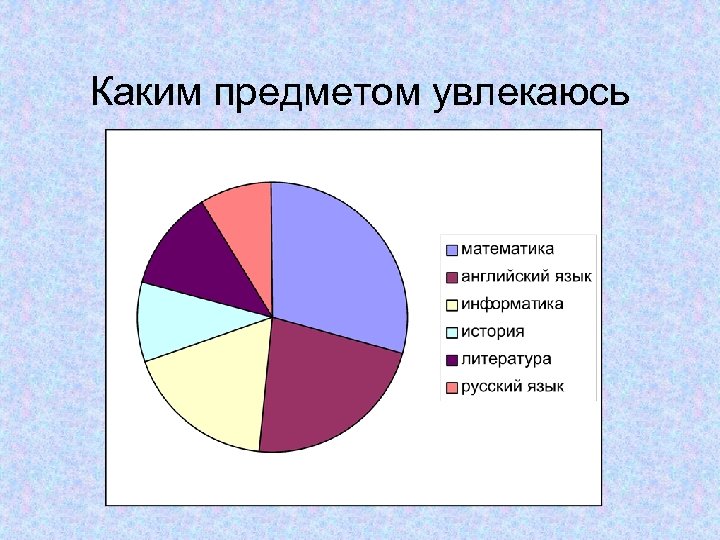Каким предметом увлекаюсь

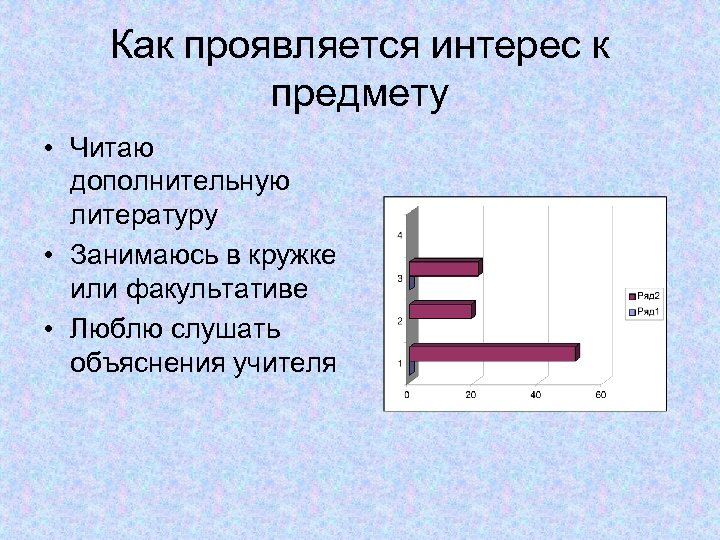Как проявляется интерес к предмету • Читаю дополнительную литературу • Занимаюсь в кружке или факультативе • Люблю слушать объяснения учителя

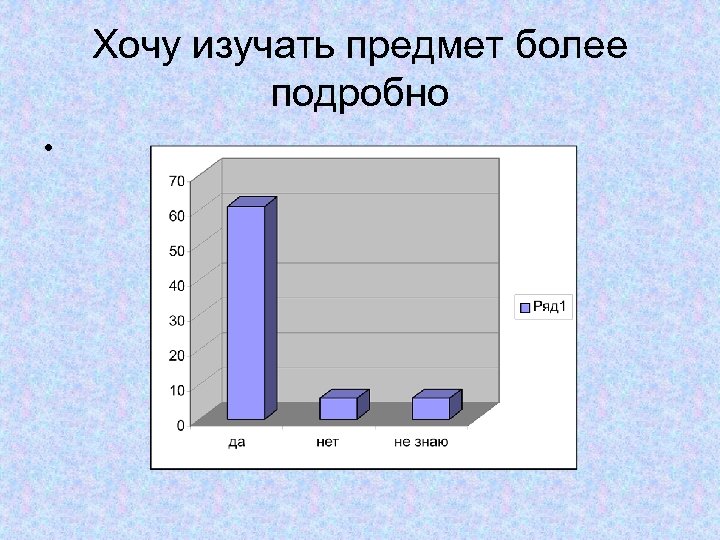Хочу изучать предмет более подробно •

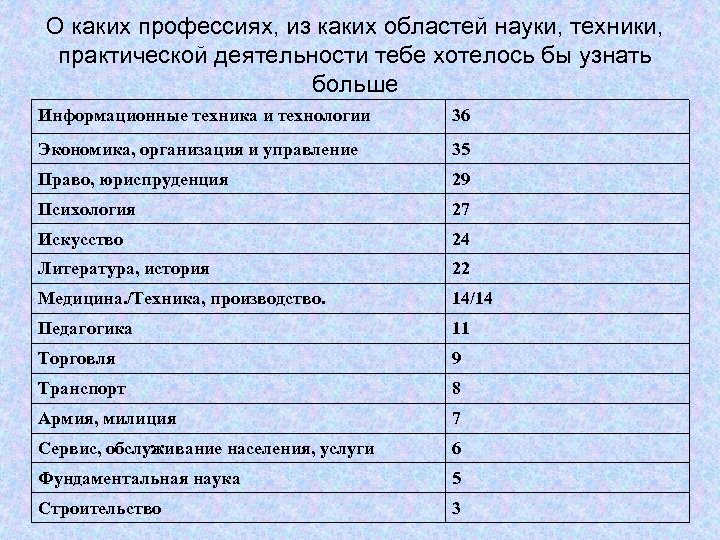О каких профессиях, из каких областей науки, техники, практической деятельности тебе хотелось бы узнать больше Информационные техника и технологии 36 Экономика, организация и управление 35 Право, юриспруденция 29 Психология 27 Искусство 24 Литература, история 22 Медицина. /Техника, производство. 14/14 Педагогика 11 Торговля 9 Транспорт 8 Армия, милиция 7 Сервис, обслуживание населения, услуги 6 Фундаментальная наука 5 Строительство 3

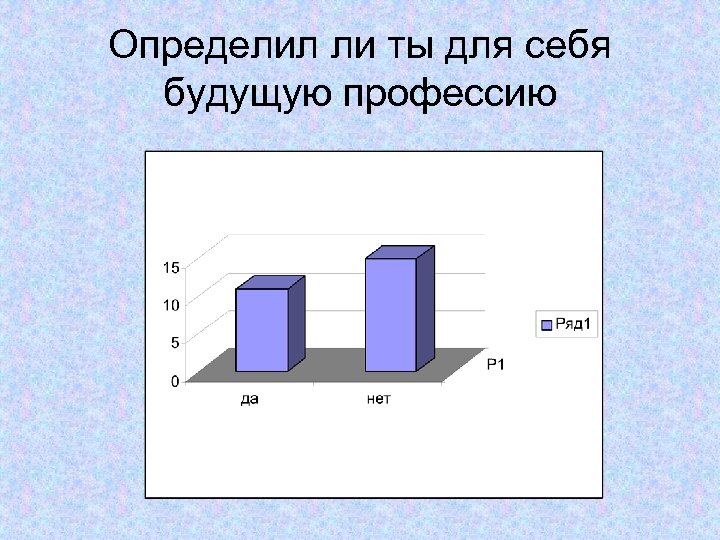Определил ли ты для себя будущую профессию

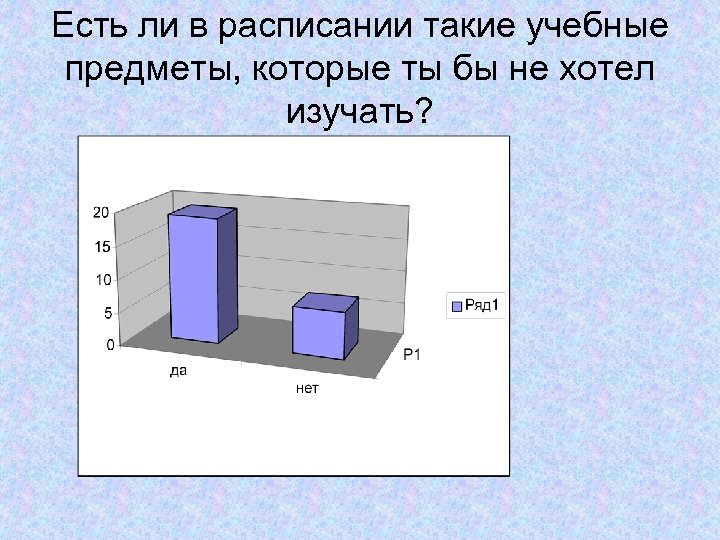Есть ли в расписании такие учебные предметы, которые ты бы не хотел изучать?

Почему именно эти предметы? • Они не пригодятся мне в будущем – 12 • Мне не интересно на этих уроках – 10 • Я вообще не понимаю, о чем там говорят – 2 • Не сложились отношения с учителем – 1 • Плохие отметки по этим предметам - 0

В каком классе ты бы хотел учиться § § § Социально-экономическом – 31 Лингвистическом – 21 Общеобразовательном – 8 Художественно-эстетическом – 7 Информационно-технологическом – 5 Химико-биологическом – 4 Физико-математическом – 3 Социально-гуманитарном – 2 Индустриально-технологическом – 1 Физико-химическом – 0 Биолого-географическом - 0

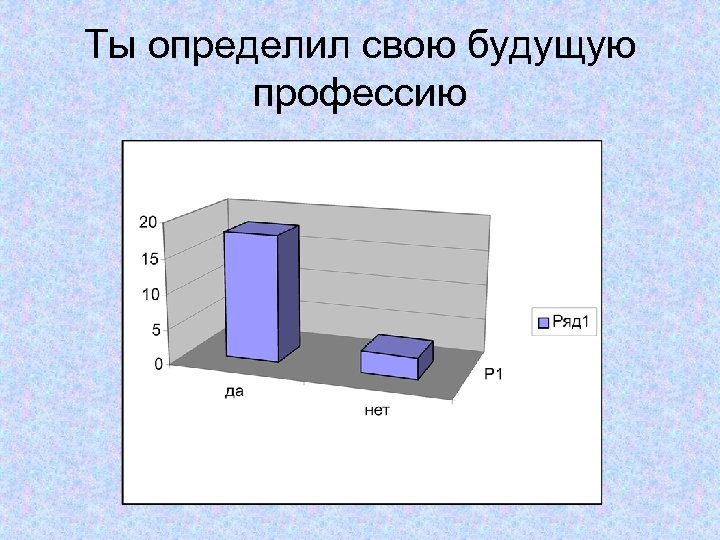Ты определил свою будущую профессию

К какой отрасли знаний или практической деятельности можно отнести выбранную профессию Экономика, организация и управление 12 Сервис, обслуживание населения, услуги 6 Торговля 4 Информационные техники и технологии 3 Психология 2 Педагогика 1 Искусство 1 Литература, история 1 Медицина 0 Строительство 0 Армия, милиция 0 Право, юриспруденция 0 Фундаментальная наука 0

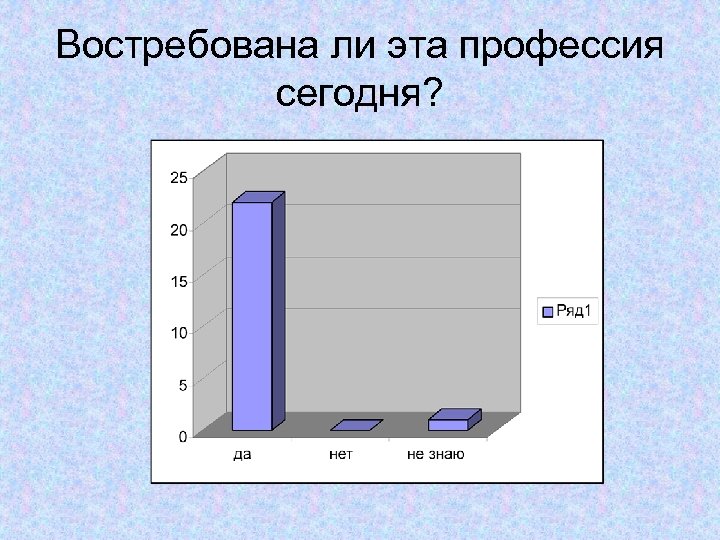Востребована ли эта профессия сегодня?

Откуда у тебя эти сведения? • СМИ – 18 • Родители – 2 • Другие источники - 2

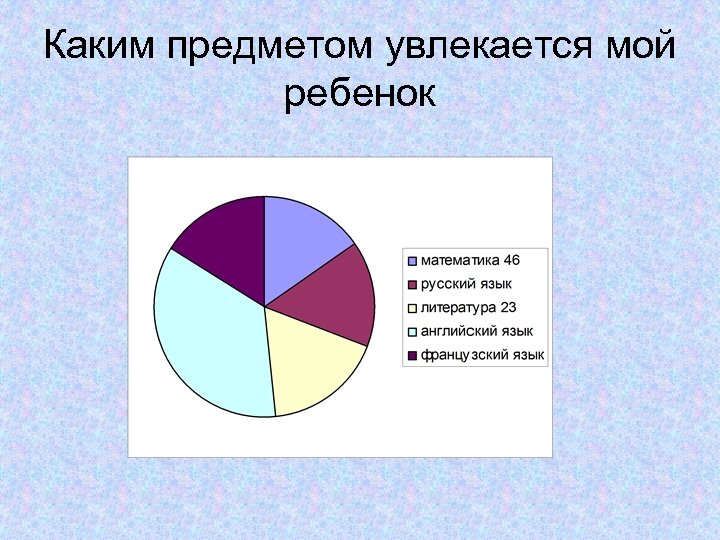Каким предметом увлекается мой ребенок

Какой профиль я выбрал для своего ребенка • • Лингвистический – 26 Социально-экономический – 19 Юридический – 6 Физико-математический – 6 Естественнонаучный – 3 Общеобразовательный – 1 Психологический - 1

Зависимость выбора профиля родителями • • • Способности ребенка – 37 Интерес – 35 Семейные традиции – 5 Бизнес – 4 Желание ребенка - 1

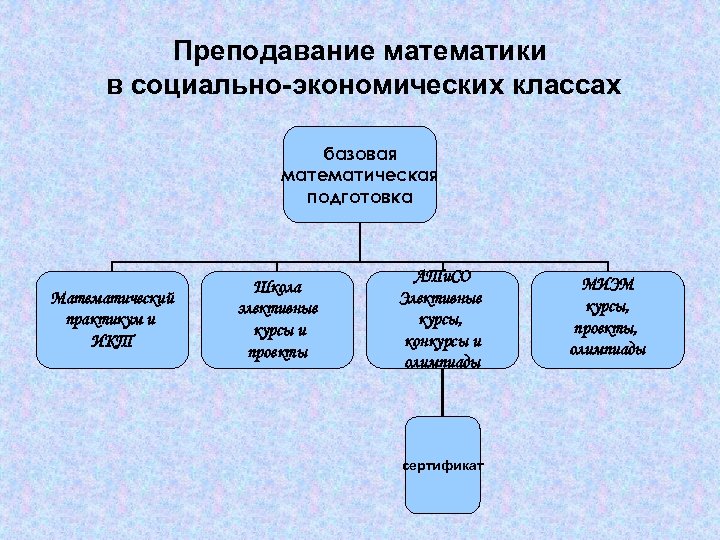Преподавание математики в социально-экономических классах базовая математическая подготовка Математический практикум и ИКТ Школа элективные курсы и проекты АТи. СО Элективные курсы, конкурсы и олимпиады сертификат МИЭМ курсы, проекты, олимпиады

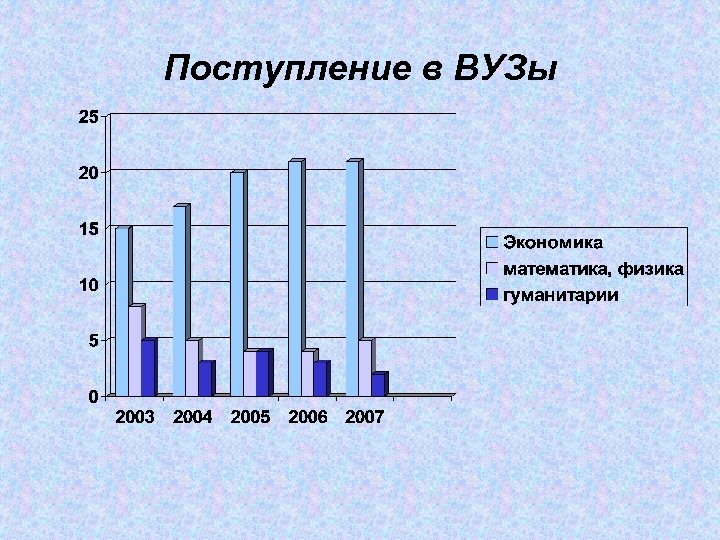Поступление в ВУЗы

Математика золотого сечения Проектная работа Ученицы 11 класса «А» Школы № 1279 Татариновой Алисы

• По мере того как продвигались мои исследования, зародилась моя ОСНОВНАЯ ГИПОТЕЗА: возможно, ряд золотого сечения обладает какими-то особенными математическимисвойствами, которые делают его такими популярными, а, следовательно, наиболее приятным для человека в целом. • Я достаточно долго размышляла над тем, чем я хочу заниматься в своей будущей жизни. Выбор все же пал на профессию архитектора. Изучая интересующую меня область, я узнала о золотом сечении, и оно заинтересовало меня. Потому моей ЦЕЛЬЮ стало проведение исследований свойств золотого сечения, а также памятников архитектуры, в пропорциональный строй которых легла эта пропорция.

Суть золотого сечения • Очевидно, что при делении целого на две неравные части возможно бесконечное множество отношений между целым и одной из его частей, а также между самими частями целого. Но только в единственном случае эти отношения могут быть равными. Этот случай и представляет собой золотое сечение, когда целое относится к большей части, как большая часть к меньшей. • Ряд золотого сечения - геометричекая прогрессия (аn=а 1 n-1). • Ряд золотого сечения обладает аддитивным свойством (а n=а n+1+а n+2). • =0, 618

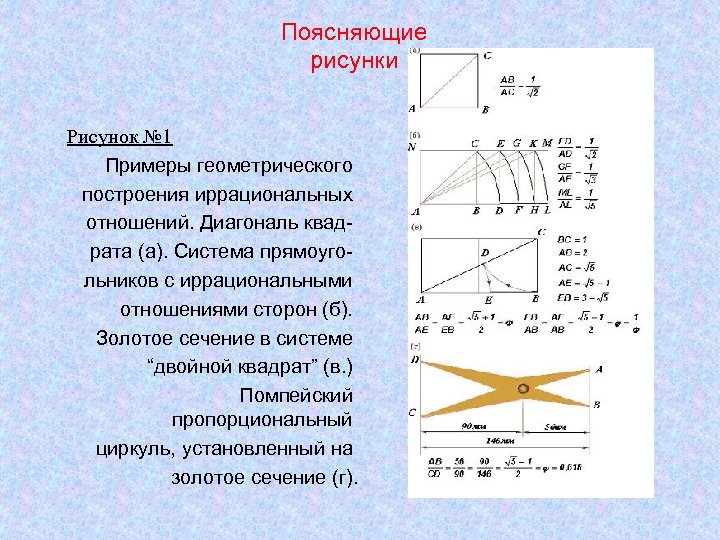Поясняющие рисунки Рисунок № 1 Примеры геометрического построения иррациональных отношений. Диагональ квадрата (а). Система прямоугольников с иррациональными отношениями сторон (б). Золотое сечение в системе “двойной квадрат” (в. ) Помпейский пропорциональный циркуль, установленный на золотое сечение (г).

Рисунок № 2 Последовательное деление единичного отрезка в золотом сечении.

Рисунок № 3 Для ряда Фибоначчи [Uk] отношение Uk+1/Uk последующего члена ряда к предыдущему с ростом k стремиться к коэффиценту золотого сечения.

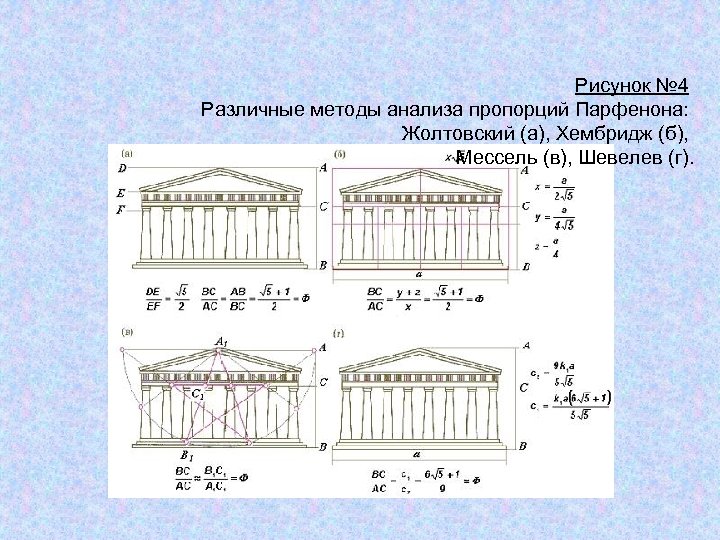Рисунок № 4 Различные методы анализа пропорций Парфенона: Жолтовский (а), Хембридж (б), Мессель (в), Шевелев (г).

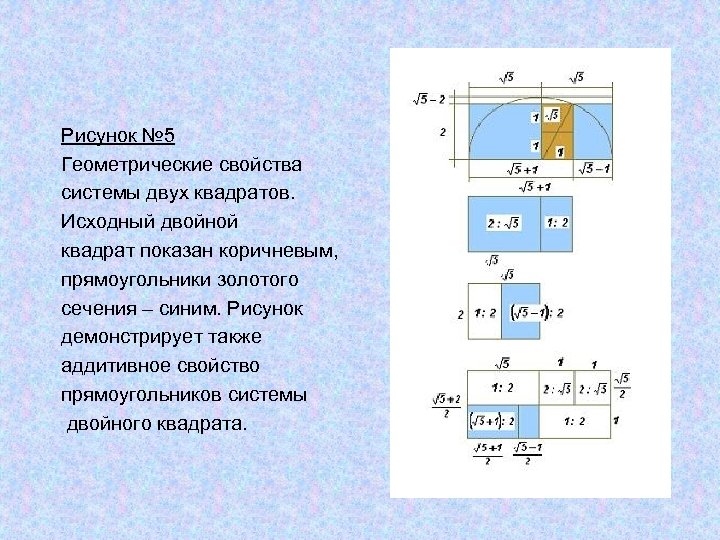Рисунок № 5 Геометрические свойства системы двух квадратов. Исходный двойной квадрат показан коричневым, прямоугольники золотого сечения – синим. Рисунок демонстрирует также аддитивное свойство прямоугольников системы двойного квадрата.

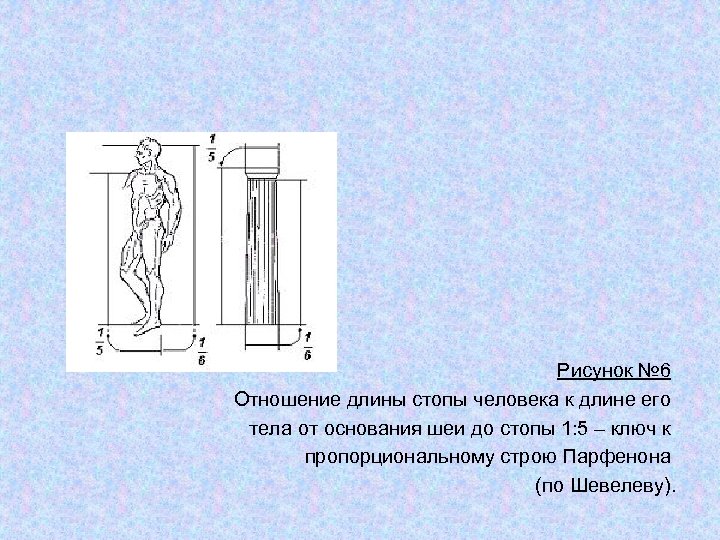Рисунок № 6 Отношение длины стопы человека к длине его тела от основания шеи до стопы 1: 5 – ключ к пропорциональному строю Парфенона (по Шевелеву).

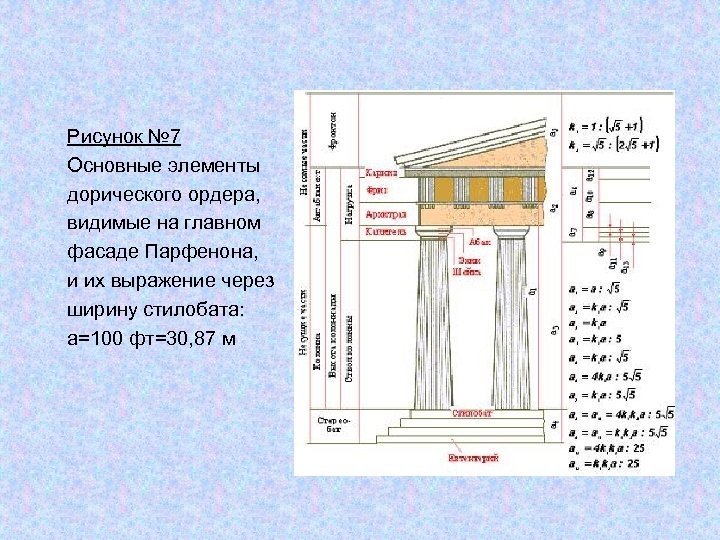Рисунок № 7 Основные элементы дорического ордера, видимые на главном фасаде Парфенона, и их выражение через ширину стилобата: а=100 фт=30, 87 м

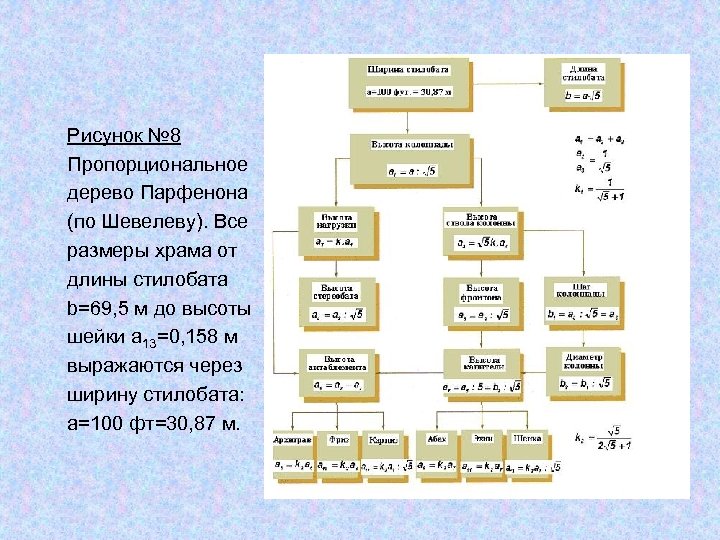Рисунок № 8 Пропорциональное дерево Парфенона (по Шевелеву). Все размеры храма от длины стилобата b=69, 5 м до высоты шейки а 13=0, 158 м выражаются через ширину стилобата: а=100 фт=30, 87 м.

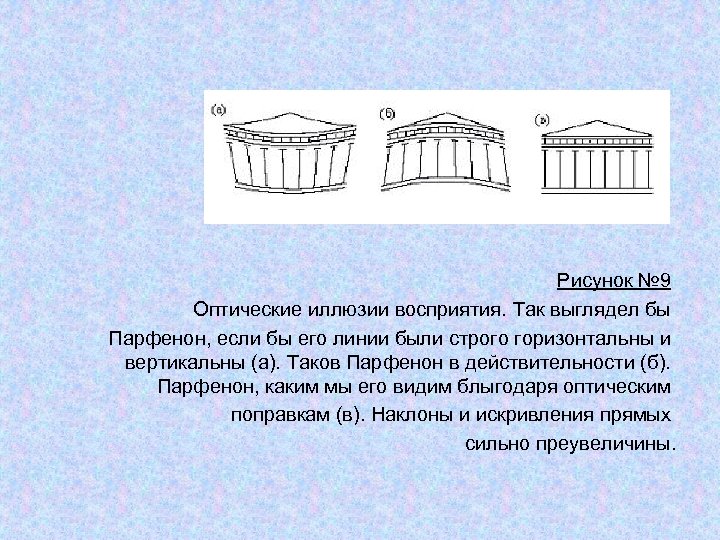Рисунок № 9 Оптические иллюзии восприятия. Так выглядел бы Парфенон, если бы его линии были строго горизонтальны и вертикальны (а). Таков Парфенон в действительности (б). Парфенон, каким мы его видим блыгодаря оптическим поправкам (в). Наклоны и искривления прямых сильно преувеличины.

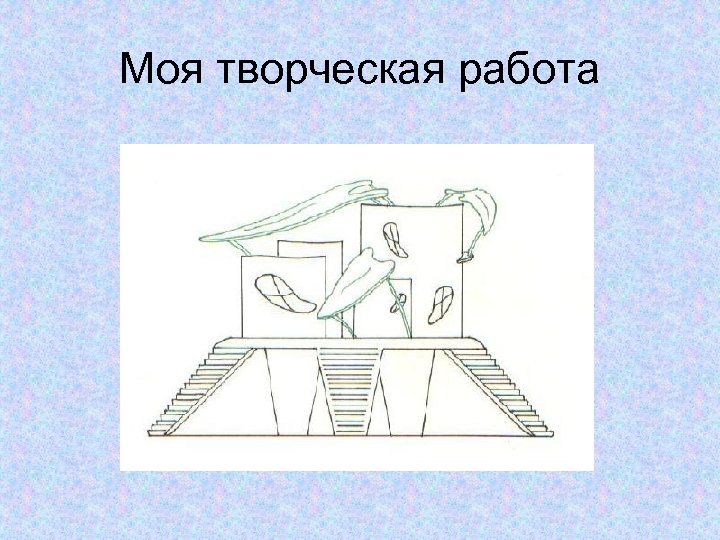Моя творческая работа

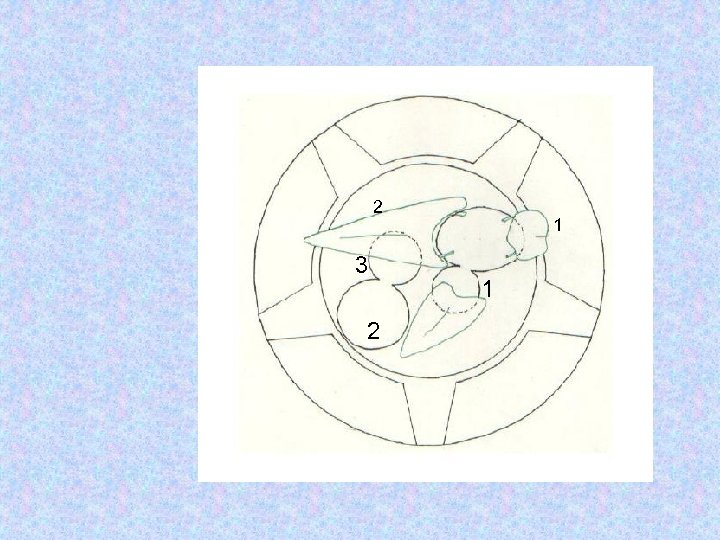2 3 2 1 1

Основные размеры • За единицу принята величина равная а=20 м. • Диаметр платформы, поддерживающей цилиндры, и общая высота строения равны этой величине. • Остальные размеры найдены с помощью коэффициента золотого сечения.

Диаметры башенок • Эллипс: » Длина=8 м. » Ширина=6 м. • Окружности: » № 1 d=4, 4 м. » № 2 d=6, 6 м. » № 3 d=5 м.

Значения первых членов , образовавшейся «золотой» прогрессии φ=12, 4 м. • • φ2=7, 6 м. • φ3=4, 7 м. • φ4=2, 9 м. ’=0, 618 • φ5=1, 8 м. • φ6=1, 1 м. • φ7=0, 7 м.

Высота башенок ØС элипсом в основании: Øh=φ2+φ4+10, 3 м. Ø№ 1: Øh 1=φ3=4, 7 м. Ø№ 2: Øh 2=φ3+φ5=6, 5 м. Ø№ 3: Øh 3=φ2=7, 6 м.

Нахождение высоты отдельных элементов строения Ø Платформа, поддерживающая полезную площадь, находится на расстояние φ2=7, 6 м. от земли. Ø Расположение листьев: Ø Лист № 1 (от платформы): Ø Верх: l 1=φ2 -φ7=11, 7 м. Ø Низ: l 2= φ2+φ6=8, 7 м. Ø Лист № 2 (от платформы): Ø Верх: l 3= φ=12, 4 м. Ø Низ: l 4= φ2=7, 6 м. Ø Поддерживающий выступ: Ø l 5= φ3+φ5=6, 5 м. Ø Длина лестницы: Ø х=9, 8 м.

Итак, ИТОГИ: • – Ряд золотого сечения геометричекая прогрессия (аn=а 1 n-1). Ø Ряд золотого сечения обладает аддитивным свойством (а n=а n+1+а n+2). Ø =0, 618 – Пропорциональное строение Парфенона все же основано на золотом сечение, и все приведенные теории лишь подтверждают это. – Выполнив творческую работу, я сумела создать то, что я по праву считаю мечтой к исполнению которой стоит стремиться. Как мне кажется, ОСНОВНЫМ РЕЗУЛЬТАТОМ проведенной работы по исследованию золотого сечения стала моя творческая работа, так как она является наиболее личной ее частью и показывает, что я могу применить полученные знания на практике. Именно в это строение я вложила всю себя, оно впитало в себя мою индивидуальность, мои мысли и мечты. Математика и золотое сечение помогли мне воплотить в жизнь мои замыслы, и это еще раз доказало то, что золотое сечение – пропорция на все времена, и она, в свою очередь, неразрывно связана с математикой.

Многогранники Платоновы тела Работу выполнили: Уч-цы 11 класса А Добрынина Дарья и Савина Жанна

Платоновы тела • Многогранники, образованные простейшими правильными многоугольниками одного типа принято называть Платоновыми телами. • Они получили свое название в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии. • Все представленные здесь многогранники (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр) являются Платоновыми телами.

Космология Платона • Четыре многогранника олицетворяли четыре сущности или «стихии» . Тетраэдр символизировал Огонь, так как его вершина устремлена вверх; Икосаэдр — Воду, так как он самый «обтекаемый» многогранник; Куб — Землю, как самый «устойчивый» многогранник; Октаэдр — Воздух, как самый «воздушный» многогранник. Пятый многогранник, Додекаэдр, воплощал в себе «все сущее» , «Вселенский разум» , символизировал все мироздание и считался главной геометрической фигурой мироздания.

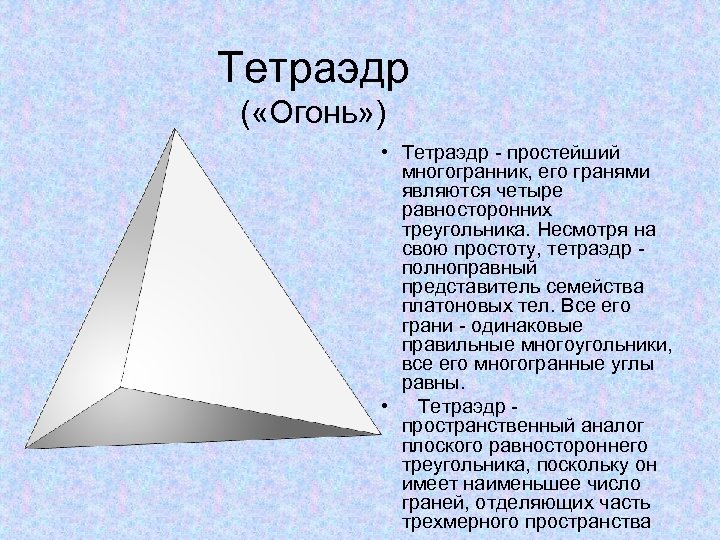Тетраэдр ( «Огонь» ) • Тетраэдр - простейший многогранник, его гранями являются четыре равносторонних треугольника. Несмотря на свою простоту, тетраэдр - полноправный представитель семейства платоновых тел. Все его грани - одинаковые правильные многоугольники, все его многогранные углы равны. • Тетраэдр - пространственный аналог плоского равностороннего треугольника, поскольку он имеет наименьшее число граней, отделяющих часть трехмерного пространства

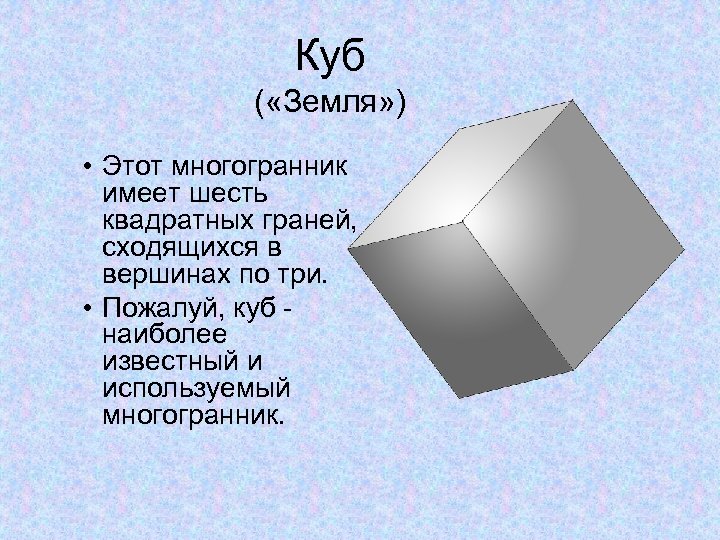Куб ( «Земля» ) • Этот многогранник имеет шесть квадратных граней, сходящихся в вершинах по три. • Пожалуй, куб - наиболее известный и используемый многогранник.

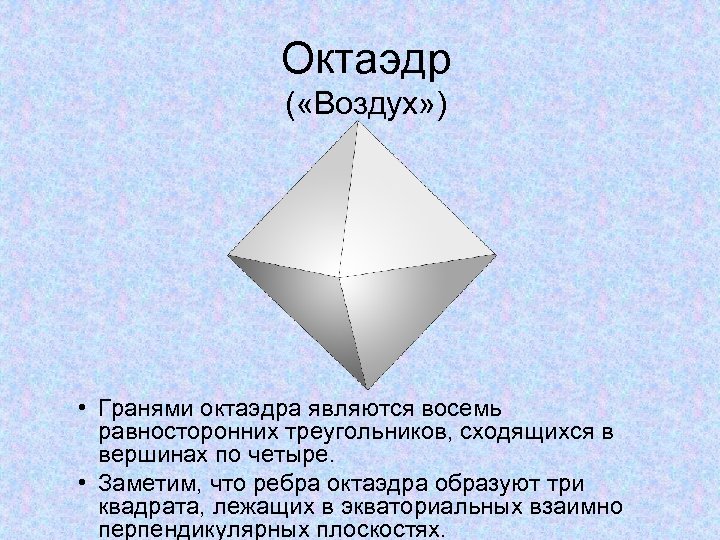Октаэдр ( «Воздух» ) • Гранями октаэдра являются восемь равносторонних треугольников, сходящихся в вершинах по четыре. • Заметим, что ребра октаэдра образуют три квадрата, лежащих в экваториальных взаимно перпендикулярных плоскостях.

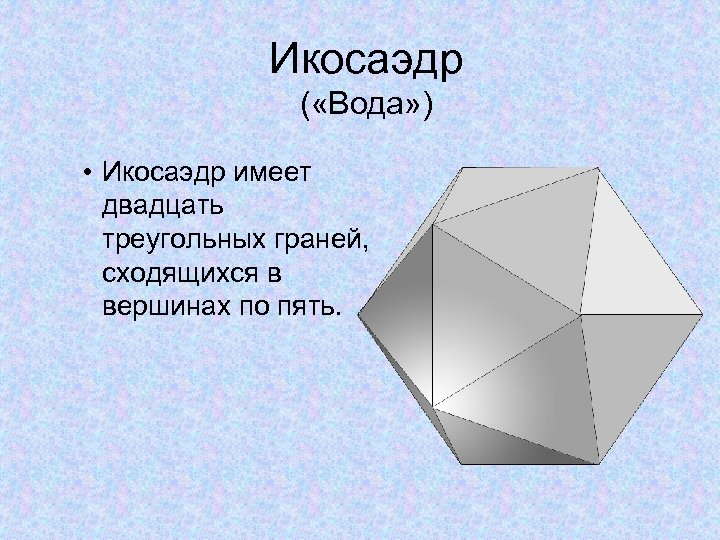Икосаэдр ( «Вода» ) • Икосаэдр имеет двадцать треугольных граней, сходящихся в вершинах по пять.

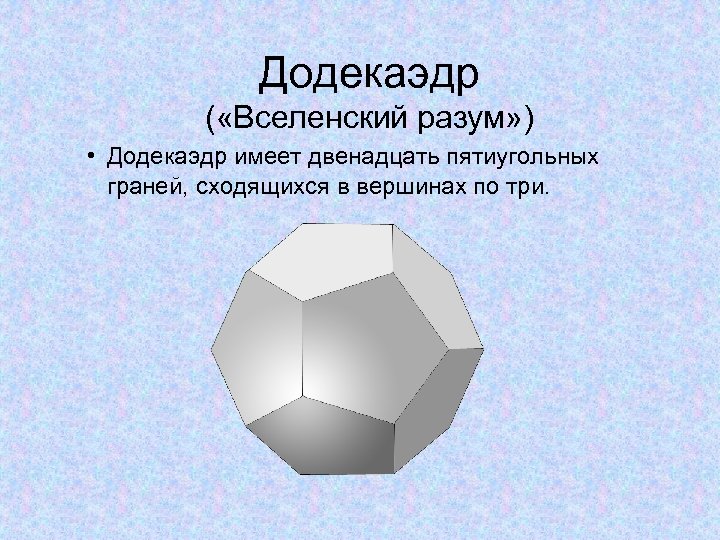Додекаэдр ( «Вселенский разум» ) • Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три.

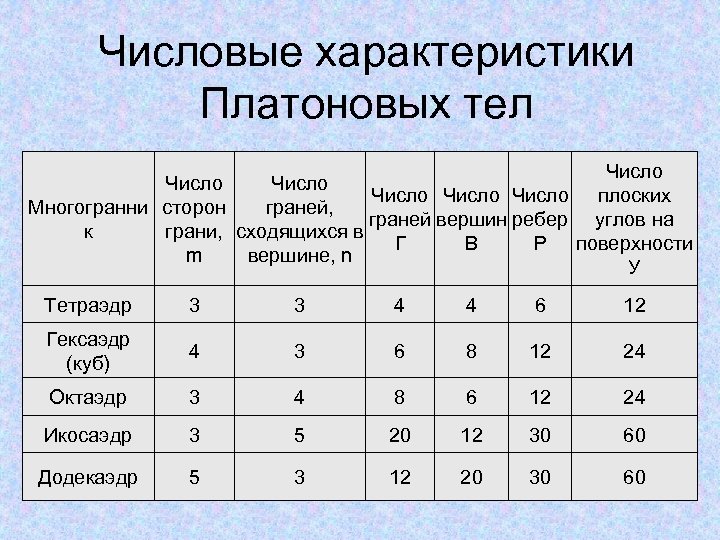Числовые характеристики Платоновых тел Число Число плоских Многогранни сторон граней, граней вершин ребер углов на к грани, сходящихся в Г В Р поверхности m вершине, n У Тетраэдр 3 3 4 4 6 12 Гексаэдр (куб) 4 3 6 8 12 24 Октаэдр 3 4 8 6 12 24 Икосаэдр 3 5 20 12 30 60 Додекаэдр 5 3 12 20 30 60

Изображение правильной пирамиды

А B Loading 10%

А B C Loading 20%

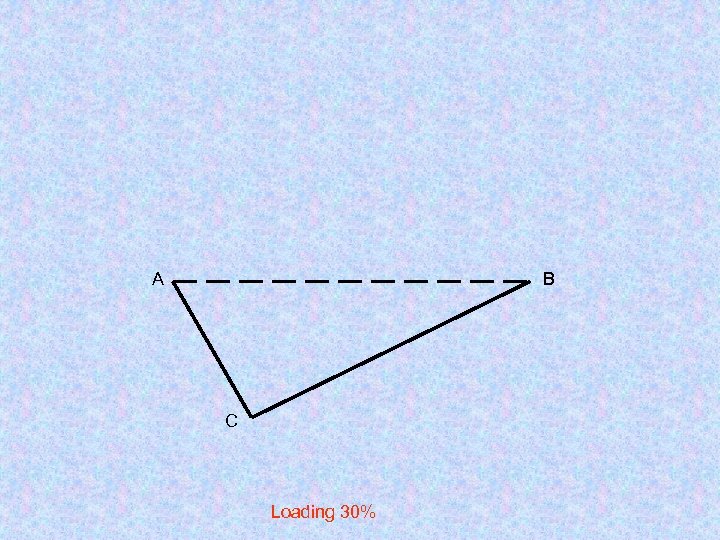А B C Loading 30%

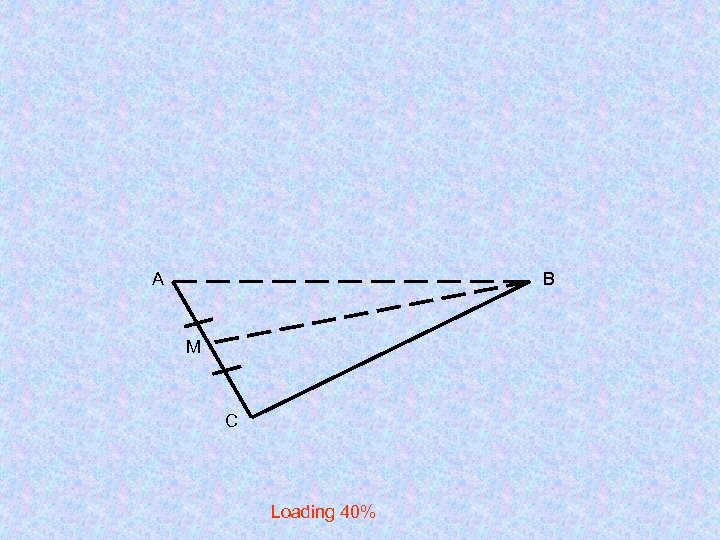А B M C Loading 40%

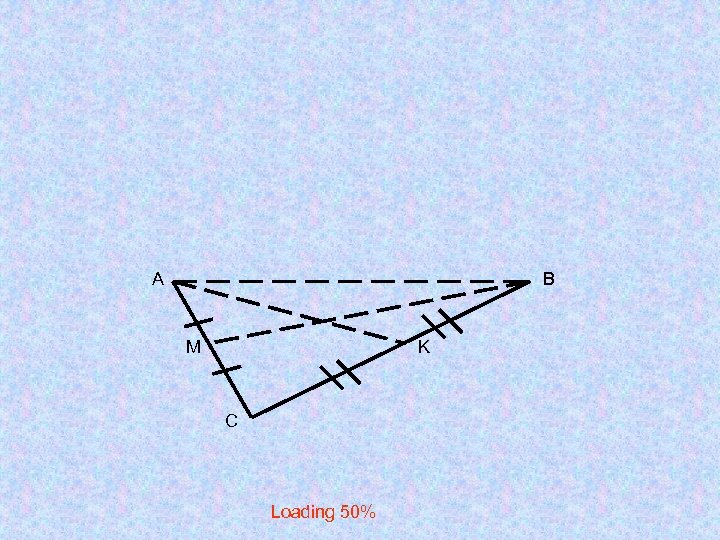А B M K C Loading 50%

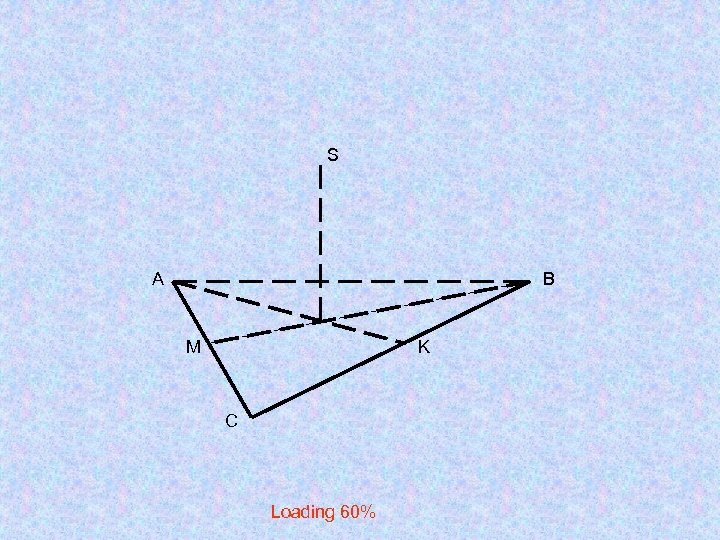S А B M K C Loading 60%

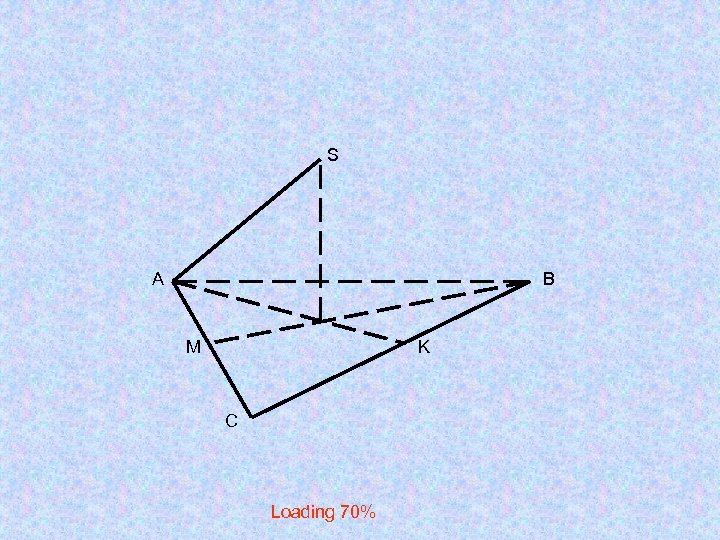S А B M K C Loading 70%

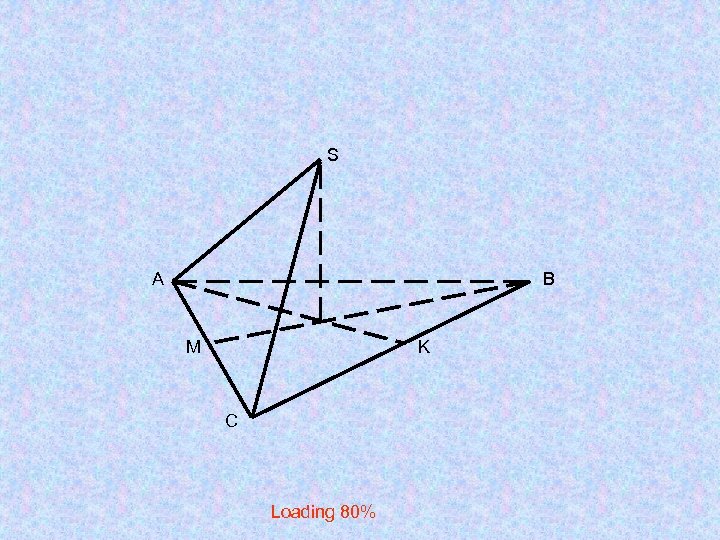S А B M K C Loading 80%

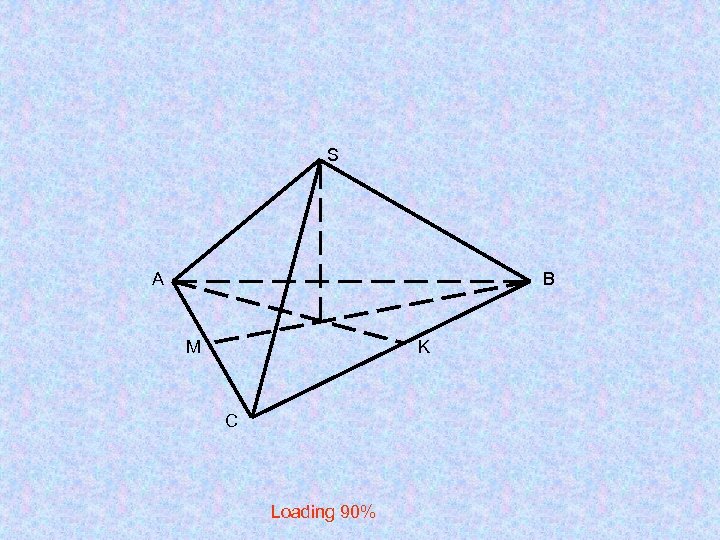S А B M K C Loading 90%

Презентация по теме: Подготовила: Луканцова Анна, 11 А класс

МНОГОГРАННИКИ Cысоева Екатерина 10 «Б»

Пимкин Владимир 11 «Б»

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ АНГЛИЙСКОГО ЯЗЫКА ШКОЛА № 1279 ЮГО-ЗАПАДНОГО ОКРУЖНОГО УПРАВЛЕНИЯ ОБРАЗОВАНИЯ ДЕПАРТАМЕНТА ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ Экзаменационная работа по геометрии и информационным технологиям в форме презентации. Тема: «Многогранники» Автор: ученица 11» А» класса Мельничук Екатерина Петровна