@ Я. Притула 1 Вступ в теорію














- Размер: 183.5 Кб
- Количество слайдов: 16
Описание презентации @ Я. Притула 1 Вступ в теорію по слайдам
 @ Я. Притула 1 Вступ в теорію ймовірностей Ярослав Притула
@ Я. Притула 1 Вступ в теорію ймовірностей Ярослав Притула
 @ Я. Притул а 2 Теорія ймовірностей: поле чудес Ви берете участь у шоу, де вам пропонують знайти приз за однією з трьох закритих дверей. Ви вибрали одні двері, після чого ведучий відкриває одні з двох інших, де немає призу і пропонує вам подумати ще раз. Чи варто змінювати свою думку? Чи варто враховувати нову інформацію? Онлайн версія гри: http: // www. stat. sc. edu/~west/javahtml/Lets. Makea. Deal. html
@ Я. Притул а 2 Теорія ймовірностей: поле чудес Ви берете участь у шоу, де вам пропонують знайти приз за однією з трьох закритих дверей. Ви вибрали одні двері, після чого ведучий відкриває одні з двох інших, де немає призу і пропонує вам подумати ще раз. Чи варто змінювати свою думку? Чи варто враховувати нову інформацію? Онлайн версія гри: http: // www. stat. sc. edu/~west/javahtml/Lets. Makea. Deal. html
 @ Я. Притул а 3 Теорія ймовірностей: як знайти ймовірність? Зазвичай, говорячи про ймовірність настання певної події, починають з опису процесу, що нас цікавить, далі, розглядаємо всеможливі результати (елементарні події), виділяємо ті, що сприяють появі цієї події, і оцінюємо ймовірність настання цієї події. Найпростіший підхід – класичний підхід, коли де m x – кількість подій, що сприяють появі події х, n – к ількість всеможливих рівноможливих подій. n m xpx)(
@ Я. Притул а 3 Теорія ймовірностей: як знайти ймовірність? Зазвичай, говорячи про ймовірність настання певної події, починають з опису процесу, що нас цікавить, далі, розглядаємо всеможливі результати (елементарні події), виділяємо ті, що сприяють появі цієї події, і оцінюємо ймовірність настання цієї події. Найпростіший підхід – класичний підхід, коли де m x – кількість подій, що сприяють появі події х, n – к ількість всеможливих рівноможливих подій. n m xpx)(
 @ Я. Притул а 4 Теорія ймовірностей: як знайти ймовірність? Часто, цього простого правила недостатньо і використовують інші підходи, зокрема емпіричний підхід (коли можна провести низку експериментів, тоді ймовірність настання події х рівна відносній частоті появи події х в цій низці повторюваних експериментів). Суб ’ єктивна оцінка ймовірності визначається на основі досвіду та суджень людини чи групи людей (як приклад – Метод Делфі ). Теоретична оцінка визначається на основі певних формул.
@ Я. Притул а 4 Теорія ймовірностей: як знайти ймовірність? Часто, цього простого правила недостатньо і використовують інші підходи, зокрема емпіричний підхід (коли можна провести низку експериментів, тоді ймовірність настання події х рівна відносній частоті появи події х в цій низці повторюваних експериментів). Суб ’ єктивна оцінка ймовірності визначається на основі досвіду та суджень людини чи групи людей (як приклад – Метод Делфі ). Теоретична оцінка визначається на основі певних формул.
 @ Я. Притул а 5 Теорія ймовірностей: правила ймовірностей Протилежна подія до А – це подія, що стається якщо не стається А. Р(А)+Р(не А)=1 Перетин подій А і Б ( ) – це подія, що стається коли одночасно настають події А і Б. Об ’ єднання (сума) подій А і Б ( )– це подія, що стається коли настає або А, або Б, або обидві одночасно. Події А і Б – несумісні, якщо Правило додавання ймовірностей : Приклад. В рулетці ймовірність випадання парного числа = 18 /37, більшого за 18 = 18 /37, парного більшого за 18 = 9 /37. Отже, ймовірність випадання або парного або більшого 18 = 18 /37+18/37 -9/37=27/37. БА БА 0 БА )()(БАРБРАРБAP
@ Я. Притул а 5 Теорія ймовірностей: правила ймовірностей Протилежна подія до А – це подія, що стається якщо не стається А. Р(А)+Р(не А)=1 Перетин подій А і Б ( ) – це подія, що стається коли одночасно настають події А і Б. Об ’ єднання (сума) подій А і Б ( )– це подія, що стається коли настає або А, або Б, або обидві одночасно. Події А і Б – несумісні, якщо Правило додавання ймовірностей : Приклад. В рулетці ймовірність випадання парного числа = 18 /37, більшого за 18 = 18 /37, парного більшого за 18 = 9 /37. Отже, ймовірність випадання або парного або більшого 18 = 18 /37+18/37 -9/37=27/37. БА БА 0 БА )()(БАРБРАРБAP
 @ Я. Притул а 6 Теорія ймовірностей: правило множення Умовна ймовірність події А при настанні додії Б – це ймовірність події А, якщо Б вже настала. Задача. Ви отримуєте приз якщо виграєте два тенісні матчі підряд. Можливими є дві схеми гри: любитель-чемпіон-любитель, або чемпіон-любитель-чемпіон. Чемпіон грає краще від любителя. Яку схему ви виберете? Правило незалежних подій. Якщо події А і Б – незалежні, то Задача. Бажаючи диверсифікувати ваші заощадження ви купили акції та облігації певної компанії. Чи зменшили ви ризик втрати коштів? )( )( )( БР БАР )()()(БРАРБАР
@ Я. Притул а 6 Теорія ймовірностей: правило множення Умовна ймовірність події А при настанні додії Б – це ймовірність події А, якщо Б вже настала. Задача. Ви отримуєте приз якщо виграєте два тенісні матчі підряд. Можливими є дві схеми гри: любитель-чемпіон-любитель, або чемпіон-любитель-чемпіон. Чемпіон грає краще від любителя. Яку схему ви виберете? Правило незалежних подій. Якщо події А і Б – незалежні, то Задача. Бажаючи диверсифікувати ваші заощадження ви купили акції та облігації певної компанії. Чи зменшили ви ризик втрати коштів? )( )( )( БР БАР )()()(БРАРБАР
 @ Я. Притул а 7 Теорія ймовірностей: дерево рішень Багато ймовірнісних задач, тобто задач з невизначеностями вирішуються за допомогою дерев рішень та дерев ймовірностей. Приклад. Ви виришуєте запустити новий товар але не впевнені в його успіх, тому було вирішено зробити дешевший пілотний проект, що дасть змогу вивчити ринок і збільшити ймовірність успіху товару, якщо ви всетаки вирішите його запускати. Ви оцінили такі ймовірності: — ймовірність успіху випуску товару = 0. 6; — ймовірність успіху в пілотному проекті = 0. 7; — ймовірність того, що успішними будуть або випуск товару або пілотний проект або обидвоє разом = 0. 75. Чи є зміст в пілотному проекті?
@ Я. Притул а 7 Теорія ймовірностей: дерево рішень Багато ймовірнісних задач, тобто задач з невизначеностями вирішуються за допомогою дерев рішень та дерев ймовірностей. Приклад. Ви виришуєте запустити новий товар але не впевнені в його успіх, тому було вирішено зробити дешевший пілотний проект, що дасть змогу вивчити ринок і збільшити ймовірність успіху товару, якщо ви всетаки вирішите його запускати. Ви оцінили такі ймовірності: — ймовірність успіху випуску товару = 0. 6; — ймовірність успіху в пілотному проекті = 0. 7; — ймовірність того, що успішними будуть або випуск товару або пілотний проект або обидвоє разом = 0. 75. Чи є зміст в пілотному проекті?
 @ Я. Притул а 8 Теорія ймовірностей: дерево ймовірностей Дерево ймовірносте й в нашому випадку буде таким: Успіх пілотног о проекту 0. 7 0. 3 так ні 0. 55 0. 15 так ні 0. 05 0. 25 так ні Тоді, наприклад, ймовірність успішного виходу товару при провальному пілотному проекті = 0. 05/0. 3=0. 167 , В той же час ймовірність успішного виходу товару при успішному пілотному проекті = 0. 5 5/0. 7 =0. 786.
@ Я. Притул а 8 Теорія ймовірностей: дерево ймовірностей Дерево ймовірносте й в нашому випадку буде таким: Успіх пілотног о проекту 0. 7 0. 3 так ні 0. 55 0. 15 так ні 0. 05 0. 25 так ні Тоді, наприклад, ймовірність успішного виходу товару при провальному пілотному проекті = 0. 05/0. 3=0. 167 , В той же час ймовірність успішного виходу товару при успішному пілотному проекті = 0. 5 5/0. 7 =0. 786.
 @ Я. Притул а 9 Теорія ймовірностей: дерево рішень Приклад. Ви вирішуєте чи виходити на ринок з новим товаром, де монополістичне становище має ваш конкурент з річним доходом в 300 тис. Якщо ви вирішуєте вийти на ринок, то можливі два варіанти – ви ділите ринок навпіл – по 100 тис. кожен (вже немає монополістичної надбавки!) або ваш конкурент починає цінову війну, в результаті якої він втратить 100 тис. , а ви 200 тис. Чи виходити на ринок з цим товаром?
@ Я. Притул а 9 Теорія ймовірностей: дерево рішень Приклад. Ви вирішуєте чи виходити на ринок з новим товаром, де монополістичне становище має ваш конкурент з річним доходом в 300 тис. Якщо ви вирішуєте вийти на ринок, то можливі два варіанти – ви ділите ринок навпіл – по 100 тис. кожен (вже немає монополістичної надбавки!) або ваш конкурент починає цінову війну, в результаті якої він втратить 100 тис. , а ви 200 тис. Чи виходити на ринок з цим товаром?
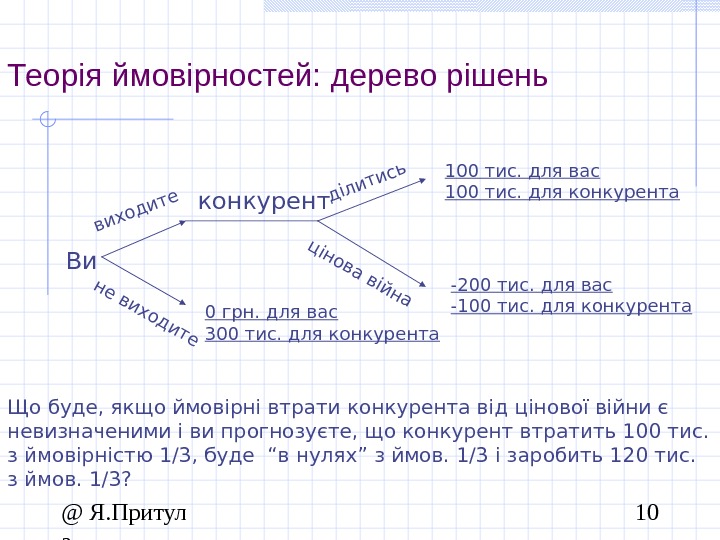
 @ Я. Притул а 10 Теорія ймовірностей: дерево рішень Вивиходите не виходите 0 грн. для вас 300 тис. для конкурентаконкурент ділитись цінова війна 100 тис. для вас 100 тис. для конкурента -200 тис. для вас -100 тис. для конкурента Що буде, якщо ймовірні втрати конкурента від цінової війни є невизначеними і ви прогнозуєте, що конкурент втратить 100 тис. з ймовірністю 1 /3 , буде “в нулях” з ймов. 1/3 і заробить 120 тис. з ймов. 1/3?
@ Я. Притул а 10 Теорія ймовірностей: дерево рішень Вивиходите не виходите 0 грн. для вас 300 тис. для конкурентаконкурент ділитись цінова війна 100 тис. для вас 100 тис. для конкурента -200 тис. для вас -100 тис. для конкурента Що буде, якщо ймовірні втрати конкурента від цінової війни є невизначеними і ви прогнозуєте, що конкурент втратить 100 тис. з ймовірністю 1 /3 , буде “в нулях” з ймов. 1/3 і заробить 120 тис. з ймов. 1/3?
 @ Я. Притул а 11 Теорія ймовірностей: суб ’ єктивність Психологи визначили, що людина часто помиляється в своїх суб ’ єктивних судженнях, особливо коли мова йде про оцінки ймовірностей малоймовірних подій.
@ Я. Притул а 11 Теорія ймовірностей: суб ’ єктивність Психологи визначили, що людина часто помиляється в своїх суб ’ єктивних судженнях, особливо коли мова йде про оцінки ймовірностей малоймовірних подій.
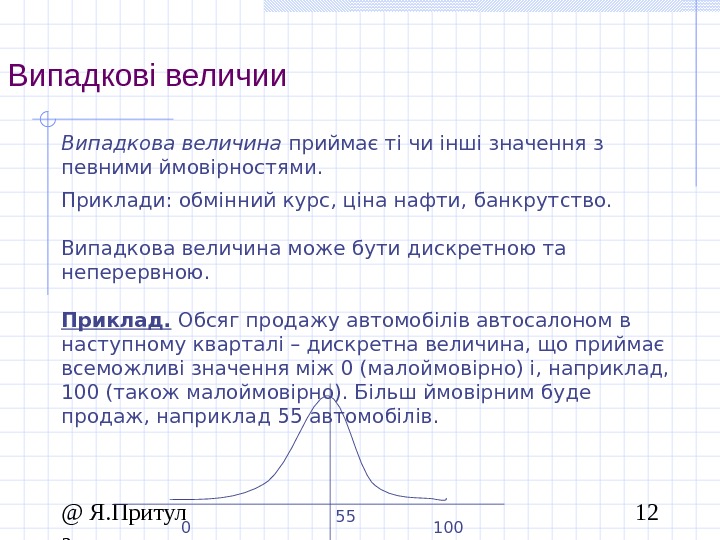
 @ Я. Притул а 12 Випадкові величии Випадкова величина приймає ті чи інші значення з певними ймовірностями. Приклади: обмінний курс, ціна нафти, банкрутство. Випадкова величина може бути дискретною та неперервною. Приклад. Обсяг продажу автомобілів автосалоном в наступному кварталі – дискретна величина, що приймає всеможливі значення між 0 (малоймовірно) і, наприклад, 100 (також малоймовірно). Більш ймовірним буде продаж, наприклад 55 автомобілів.
@ Я. Притул а 12 Випадкові величии Випадкова величина приймає ті чи інші значення з певними ймовірностями. Приклади: обмінний курс, ціна нафти, банкрутство. Випадкова величина може бути дискретною та неперервною. Приклад. Обсяг продажу автомобілів автосалоном в наступному кварталі – дискретна величина, що приймає всеможливі значення між 0 (малоймовірно) і, наприклад, 100 (також малоймовірно). Більш ймовірним буде продаж, наприклад 55 автомобілів.
 @ Я. Притул а 13 Випадкові величии Ці ж дані можна подати в таблиці: Щоб знайти найбільш очікуване значення (математичне сподівання) треба: Яка різниця між середнім значенням та математичним сподіванням? Х 0 1 2 3. . . 52 53 54 55 56 57. . . 98 99 10 0 р 0. 0 1 0. 0 2. . . 0. 0 6 0. 0 7 0. 0 8 0. 0 9 0. 0 8 0. 0 1 1 ipiip. XXE)(
@ Я. Притул а 13 Випадкові величии Ці ж дані можна подати в таблиці: Щоб знайти найбільш очікуване значення (математичне сподівання) треба: Яка різниця між середнім значенням та математичним сподіванням? Х 0 1 2 3. . . 52 53 54 55 56 57. . . 98 99 10 0 р 0. 0 1 0. 0 2. . . 0. 0 6 0. 0 7 0. 0 8 0. 0 9 0. 0 8 0. 0 1 1 ipiip. XXE)(
 @ Я. Притул а 14 Випадкові величии Щоб знайти стандартне відхилення випадкової величини треба: Яка різниця між стандартним відхиленням даних та стандартним відхиленням випадкової величини? Приклад. Ви розглядаєте можливість інвестиції 12 тис. в три проекти А, В та С. Через рік проект А гарантовано дає 14 тис. , проект В дає або 10 тис. або 20 тис. з ймовірністю 0. 5, проект С дає 0 з ймов. 0. 98 і 1 млн з ймов. 0. 02. Куди вам інвестувати? Очікувана дохідність проектів, Е(А)=14000, Е(В)=10000*0. 5+20000*0. 5=15000, Е(С)=0*0. 98+1000000*0. 02=20000. Невже С – найкращий проект? iip. XXsd 2 )()(
@ Я. Притул а 14 Випадкові величии Щоб знайти стандартне відхилення випадкової величини треба: Яка різниця між стандартним відхиленням даних та стандартним відхиленням випадкової величини? Приклад. Ви розглядаєте можливість інвестиції 12 тис. в три проекти А, В та С. Через рік проект А гарантовано дає 14 тис. , проект В дає або 10 тис. або 20 тис. з ймовірністю 0. 5, проект С дає 0 з ймов. 0. 98 і 1 млн з ймов. 0. 02. Куди вам інвестувати? Очікувана дохідність проектів, Е(А)=14000, Е(В)=10000*0. 5+20000*0. 5=15000, Е(С)=0*0. 98+1000000*0. 02=20000. Невже С – найкращий проект? iip. XXsd 2 )()(
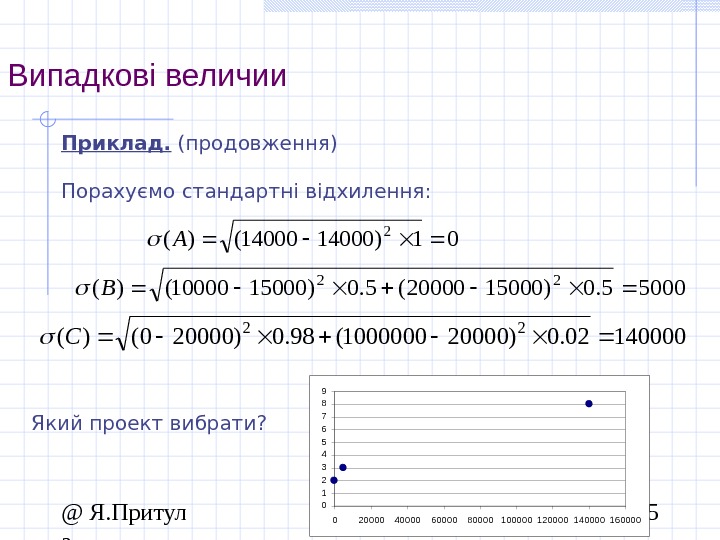
 @ Я. Притул а 15 Випадкові величии Приклад. (продовження) Порахуємо стандартні відхилення: 01)14000()( 2 A 50005. 0)1500020000(5. 0)1500010000()( 22 B 14000002. 0)200001000000(98. 0)200000()( 22 C 0123456789 0 20000 40000 60000 80000 100000 120000 140000 160000 Який проект вибрати?
@ Я. Притул а 15 Випадкові величии Приклад. (продовження) Порахуємо стандартні відхилення: 01)14000()( 2 A 50005. 0)1500020000(5. 0)1500010000()( 22 B 14000002. 0)200001000000(98. 0)200000()( 22 C 0123456789 0 20000 40000 60000 80000 100000 120000 140000 160000 Який проект вибрати?
 @ Я. Притул а 16 Математичні дії над випадковими величинами Множення випадкової величини на константу Додавання випадкових величин Множення випадкових величин Х+Х = 2 Х ?
@ Я. Притул а 16 Математичні дії над випадковими величинами Множення випадкової величини на константу Додавання випадкових величин Множення випадкових величин Х+Х = 2 Х ?

