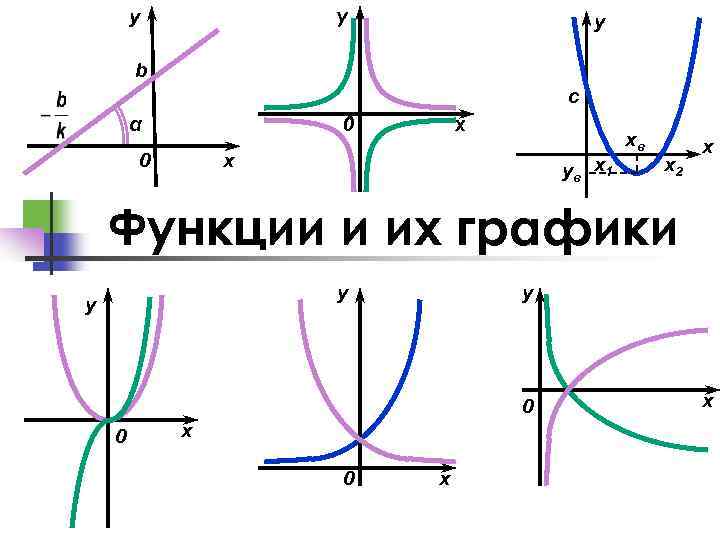
y y y b c 0 α 0 x x ув x 1 xв x 2 x Функции и их графики y y y 0 0 x x

Содержание n Функции и их графики. n Преобразование графиков функций. n Свойства функций.

Функции. Линейная функция Квадратичная функция Степенная функция Обратная пропорциональность Показательная функция Логарифмическая функция Тригонометрические функции
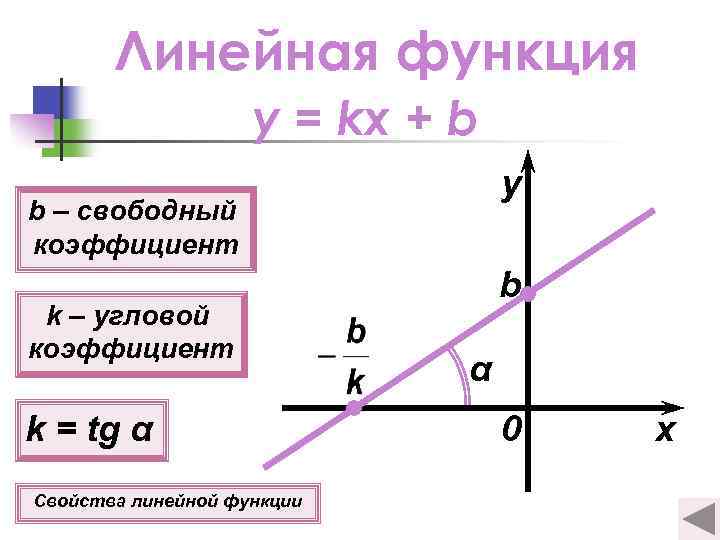
Линейная функция y = kx + b y b – свободный коэффициент k – угловой коэффициент k = tg α Свойства линейной функции b α 0 x
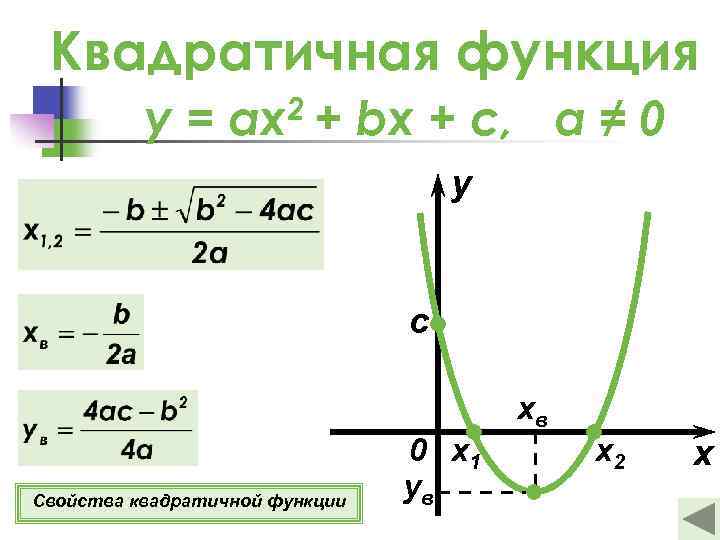
Квадратичная функция y = ax 2 + bx + c, а ≠ 0 y c xв Свойства квадратичной функции 0 x 1 ув x 2 x

Степенная функция y = xn y y = xn, где n = 2 k, k Z y = xn, где n = 2 k +1, k Z 1 01 Свойства степенной функции x
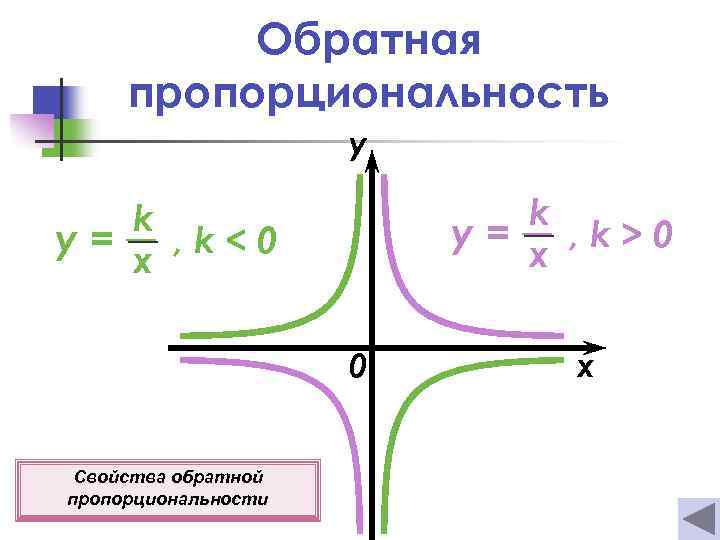
Обратная пропорциональность y k y= , k>0 x k y= , k<0 x 0 Свойства обратной пропорциональности x
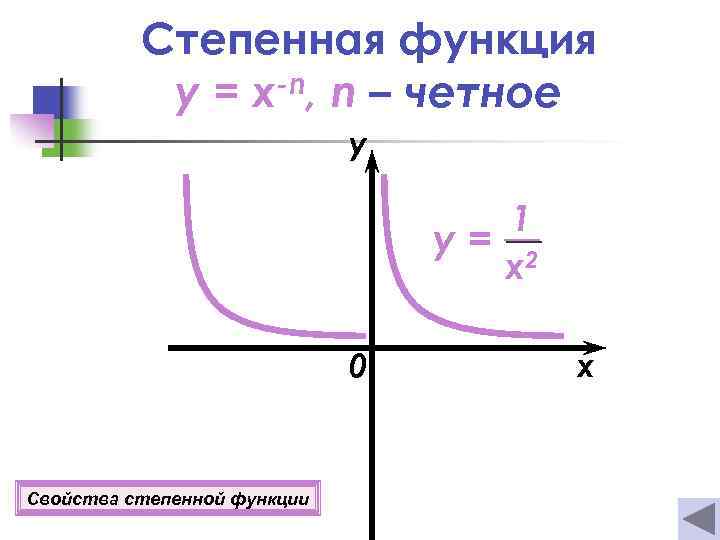
Степенная функция y = x-n, n – четное y 1 y= 2 x 0 Свойства степенной функции x
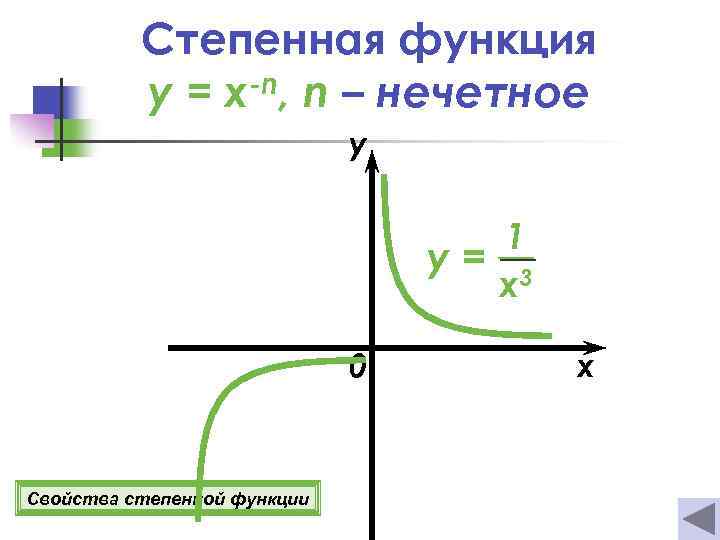
Степенная функция y = x-n, n – нечетное y 1 y= 3 x 0 Свойства степенной функции x
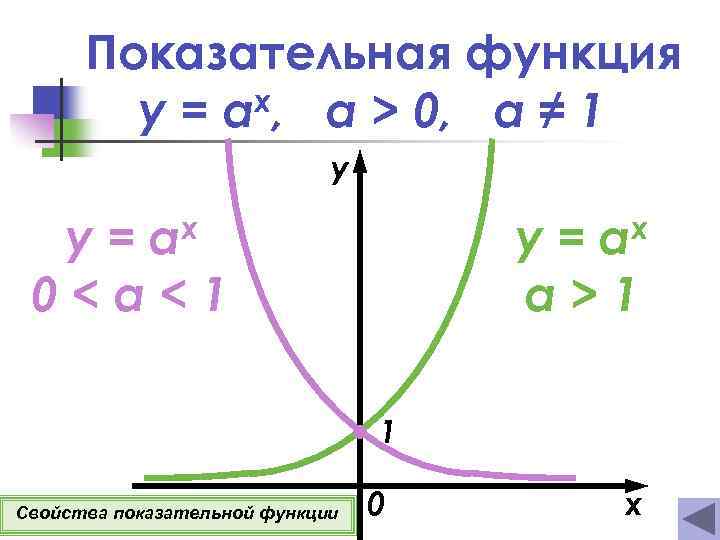
Показательная функция y = ax, а > 0, a ≠ 1 y x a y= 0<a<1 y= a>1 1 Свойства показательной функции 0 x
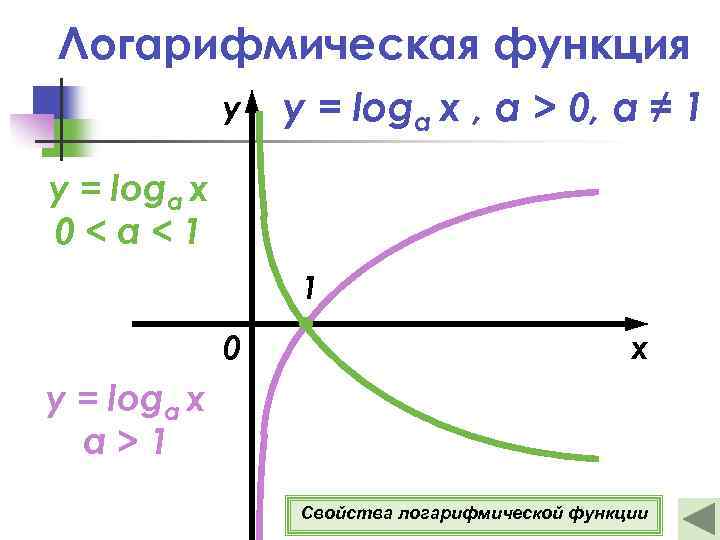
Логарифмическая функция y y = loga x , а > 0, a ≠ 1 y = loga x 0<a<1 1 0 x y = loga x a>1 Свойства логарифмической функции
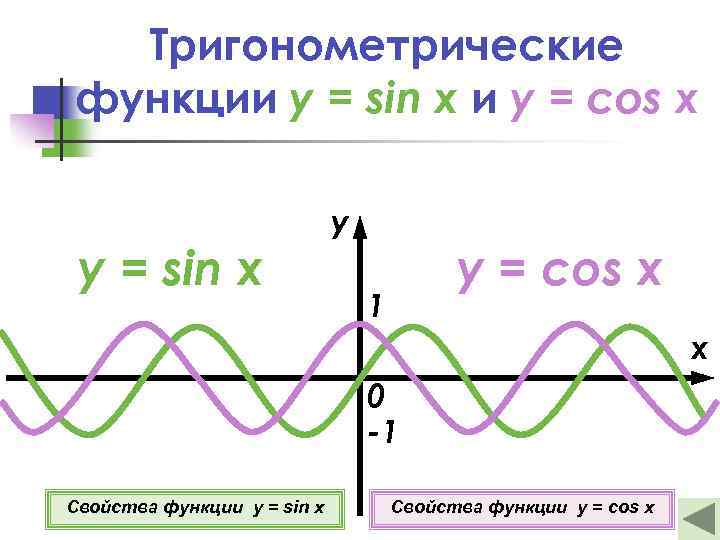
Тригонометрические функции y = sin x и y = cos x y = sin x y y = cos x 1 x 0 -1 Свойства функции y = sin x Свойства функции y = cos x
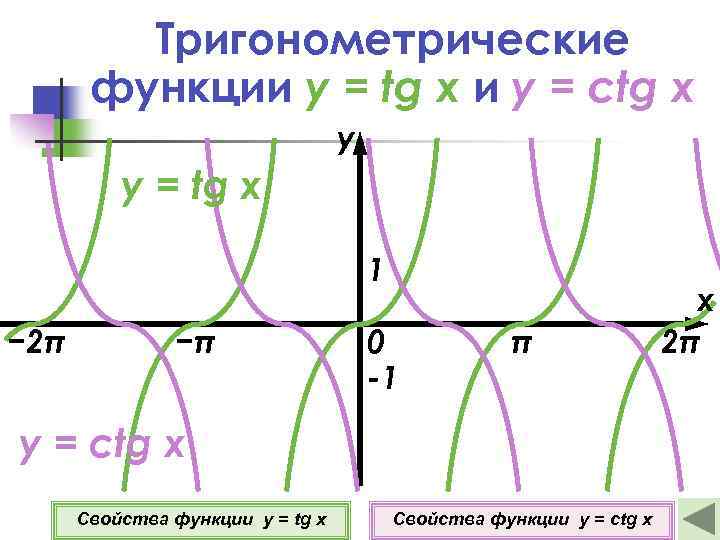
Тригонометрические функции y = tg x и y = ctg x у y = tg x 1 − 2π −π 0 -1 π y = ctg x Свойства функции y = ctg x x 2π

Геометрические преобразования графиков Преобразование вида y = f(x)+ b Преобразование вида y = f(x – a) Преобразование вида y = kf(x) Преобразование вида y = f(mx) Преобразование вида y = |f(x)| Преобразование вида y = f(|x|) Преобразование вида |y|= f(x)
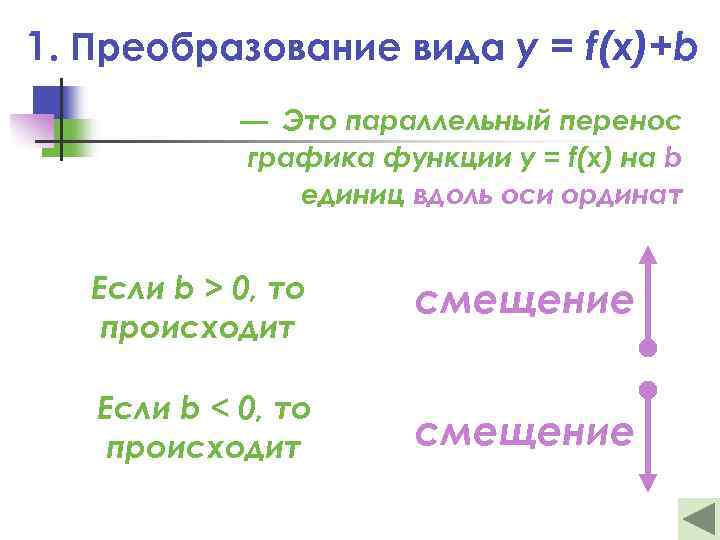
1. Преобразование вида y = f(x)+b — Это параллельный перенос графика функции y = f(x) на b единиц вдоль оси ординат Если b > 0, то происходит смещение Если b < 0, то происходит смещение
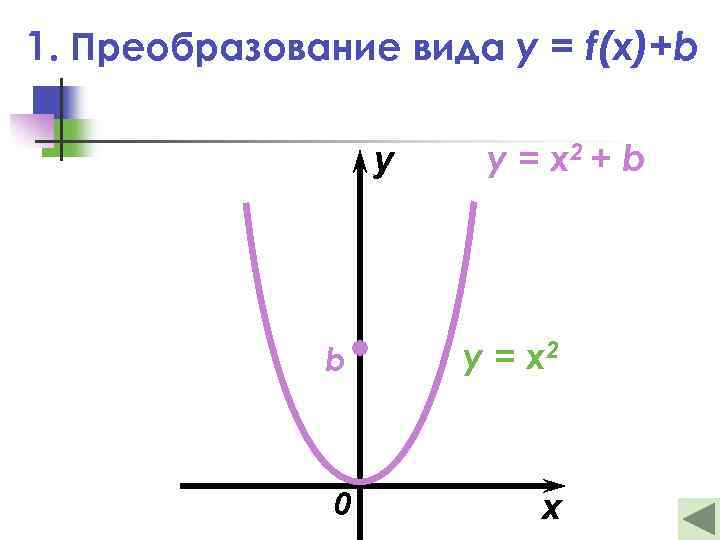
1. Преобразование вида y = f(x)+b y y = x 2 + b b y = x 2 0 x
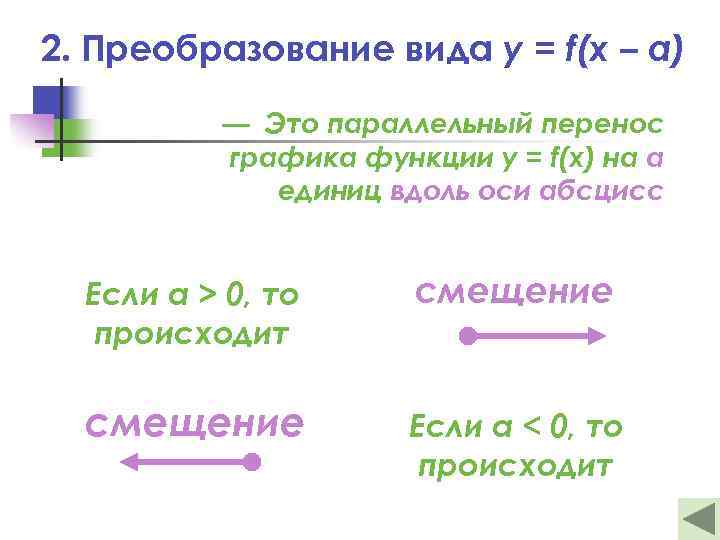
2. Преобразование вида y = f(x – a) — Это параллельный перенос графика функции y = f(x) на а единиц вдоль оси абсцисс Если а > 0, то происходит смещение Если а < 0, то происходит
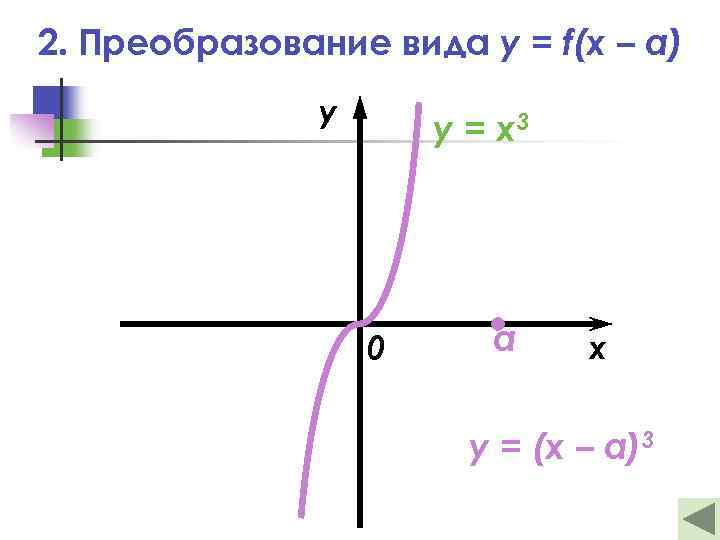
2. Преобразование вида y = f(x – a) y y = x 3 0 a x y = (x – a)3
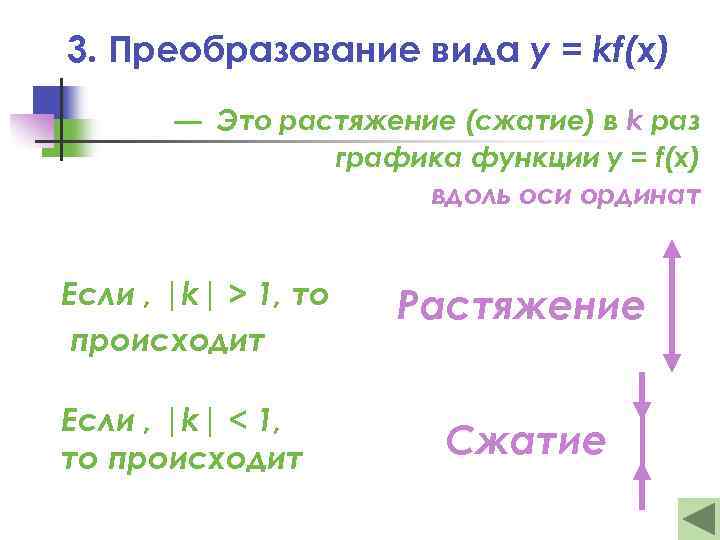
3. Преобразование вида y = kf(x) — Это растяжение (сжатие) в k раз графика функции y = f(x) вдоль оси ординат Если , |k| > 1, то происходит Если , |k| < 1, то происходит Растяжение Сжатие
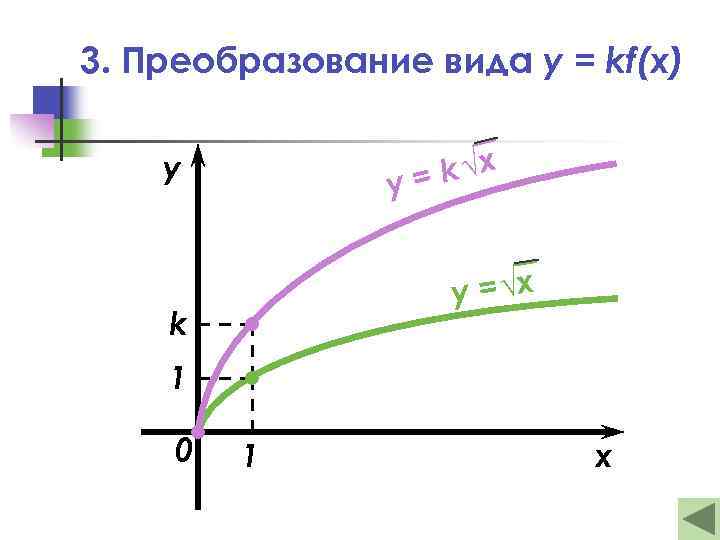
3. Преобразование вида y = kf(x) k √х у= y у = √х k 1 0 1 x
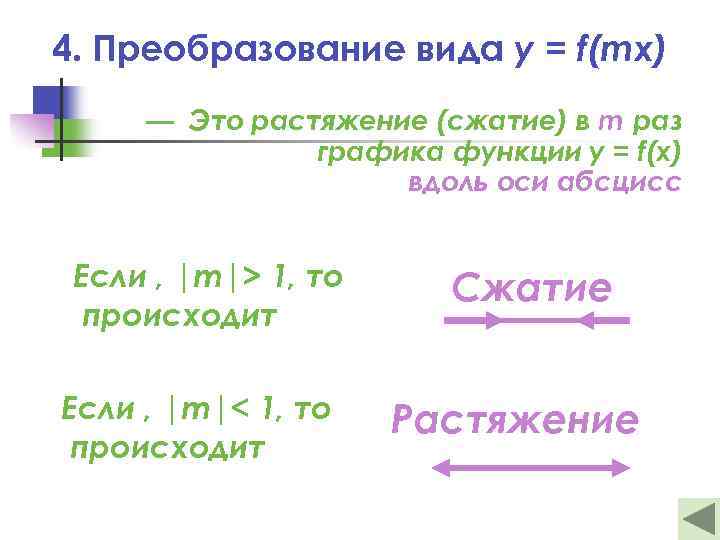
4. Преобразование вида y = f(mx) — Это растяжение (сжатие) в m раз графика функции y = f(x) вдоль оси абсцисс Если , |m|> 1, то происходит Если , |m|< 1, то происходит Сжатие Растяжение
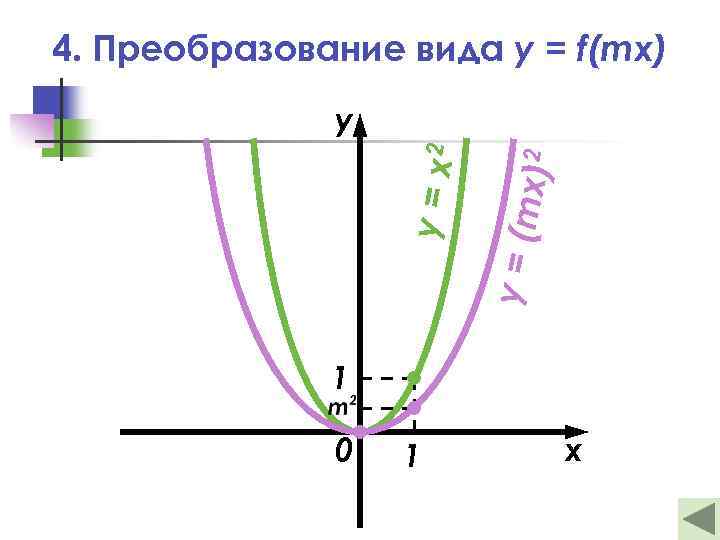
4. Преобразование вида y = f(mx) x) 2 y = (m y = x 2 y 1 0 1 x

5. Преобразование вида y = |f(x)| — Это отображение нижней части графика функции y = f(x) в верхнюю полуплоскость относительно оси абсцисс с сохранением верхней части графика у y = |f(x)| y = f(x) х 0
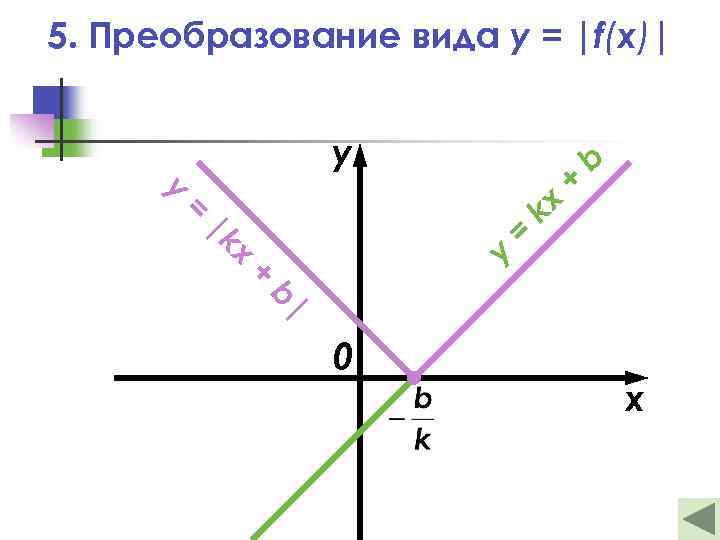
5. Преобразование вида y = |f(x)| b + x kx |k + = = y y y b| 0 x
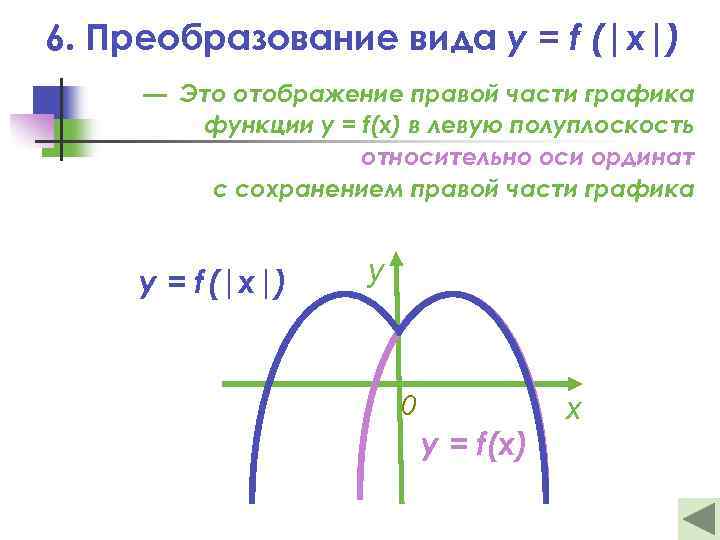
6. Преобразование вида y = f (|x|) — Это отображение правой части графика функции y = f(x) в левую полуплоскость относительно оси ординат с сохранением правой части графика y = f (|x|) у 0 y = f(x) х
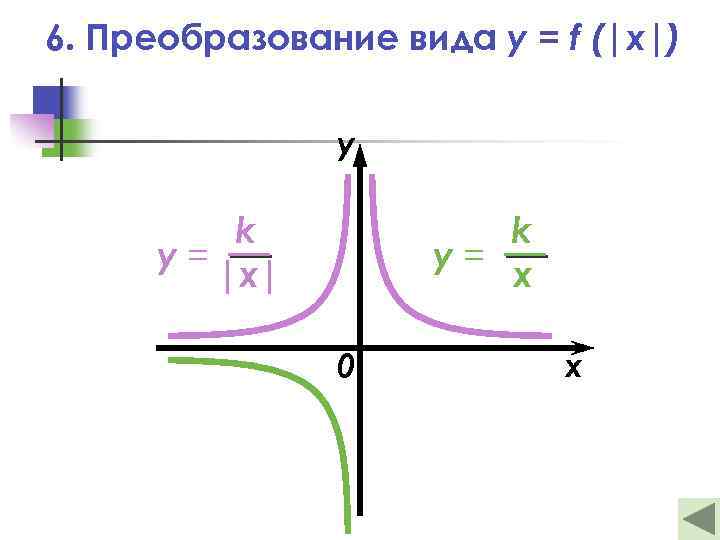
6. Преобразование вида y = f (|x|) y k у= |x| k у= x 0 x
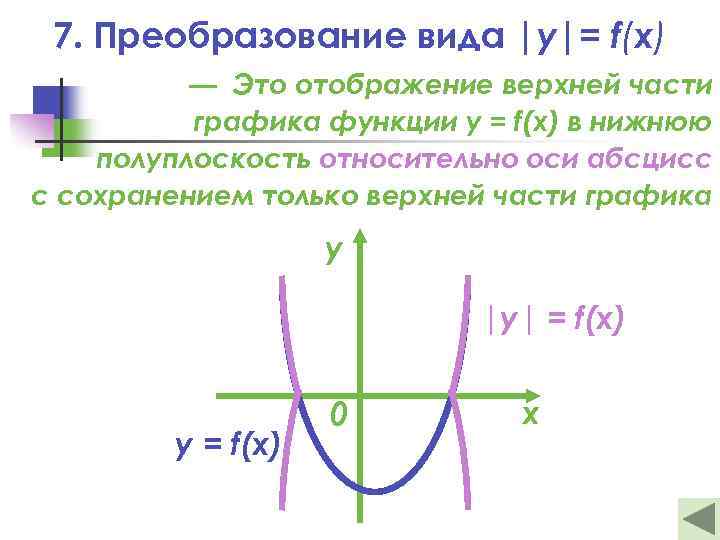
7. Преобразование вида |y|= f(x) — Это отображение верхней части графика функции y = f(x) в нижнюю полуплоскость относительно оси абсцисс с сохранением только верхней части графика у |y| = f(x) х y = f(x) 0
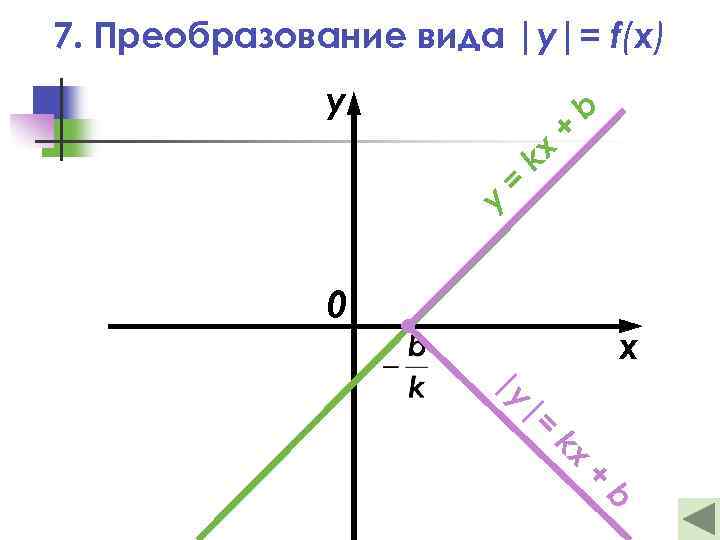
7. Преобразование вида |y|= f(x) y = kx + b y 0 x |y |= kx + b

Свойства функций • Свойства линейной функции • Свойства квадратичной функции • Свойства степенной функции • Свойства обратной пропорциональности • Свойства показательной функции • Свойства логарифмической функции • Свойства тригонометрических функций: y = sin x y = tg x y = cos x y = ctg x

Свойства линейной функции y = kx + b 1 о D(y) = (−∞; +∞); E(y) = (−∞; +∞). 2 о Если b = 0, то функция нечетная. Если b ≠ 0, то функция ни четная, ни нечетная. b о Если х = 0, то у = b, если у = 0, то х = − 3. k 4 о Если k > 0, то функция возрастает при х (−∞; +∞). Если k < 0, то функция убывает при х (−∞; +∞).

Свойства квадратичной функции y= 2+ ax bx + c, а ≠ 0 1 о D(y) = (−∞; +∞). 2 о Если a > 0, то E(y) = [ув ; +∞); Если a < 0, то E(y) = (−∞; ув ]. 3 о Если b = 0, то функция четная. Если b ≠ 0, то функция ни четная, ни нечетная. - b ± √ b 2 -4 ac о Если х = 0, то у = c, если у = 0, то х 4 1, 2 = 2 a 5 о Если a > 0, то функция возрастает при х [xв ; +∞); функция убывает при х (−∞; хв ]. Если a < 0, то функция возрастает при х (−∞; хв ]; функция убывает при х [xв ; +∞). Подробнее

Свойства степенной функции y= n x Если n = 2 k, где k Z Если n = 2 k +1, где k Z 1 о D(y)=(−∞; +∞). 2 о E(y)=[0 ; +∞). 2 о E(y)=(−∞; +∞). 3 о Функция четная. 3 о Функция нечетная. 4 о Если х = 0, то у = 0. 5 о Функция возрастает при х [0 ; +∞); убывает при х (−∞; 0]. при х (−∞; +∞).

Свойства обратной пропорциональности k у= x 1 о D(y) = (−∞; 0)u(0; +∞) 2 о E(y) = (−∞; 0)u(0 ; +∞) 3 о Функция нечетная. 4 о х ≠ 0, у ≠ 0. 5 о Если k > 0, то функция убывает при х (−∞; 0)u(0; +∞). Если k < 0, то функция возрастает при х (−∞; 0)u(0; +∞).

Свойства степенной функции y= -n x Если n = 2 k, где k Z Если n = 2 k +1, где k Z 1 о D(y)=(−∞; 0)U(0; +∞). 2 о E(y)=(0 ; +∞). 2 о E(y)=(−∞; 0)U(0; +∞). 3 о Функция четная. 4 о Если х = 1, то у = 1. 5 о Функция возрастает при х (−∞; 0); убывает при х (0 ; +∞). 6º функция ограничена снизу прямой у = 0. 3 о Функция нечетная. 4 о Если х = 1, то у = 1; если х = -1, то у = -1. 5 о Функция убывает при х (−∞; 0); (0; +∞). 6º Функция не ограничена

Свойства показательной функции y= x, a а > 0, a ≠ 1 1 о D(y)=(−∞; +∞). 2 о E(y)=(0 ; +∞). 3 о Функция ни четная, ни нечетная. 4 о Если х = 0, то у = 1. 5 о Если а > 1, то функция возрастает при х (−∞; +∞). Если 0 < а < 1, то функция убывает при х (−∞; +∞). Подробнее

Свойства логарифмической функции y = loga x , а > 0, a ≠ 1 1 о D(y)= (0 ; +∞). 2 о E(y)= (−∞; +∞). 3 о Функция ни четная, ни нечетная. 4 о Если х = 1 , то у = 0. 5 о Если а > 1, то функция возрастает при х (0; +∞). Если 0 < а < 1, то функция убывает при х (0; +∞). Подробнее

Свойства функции y = sin x 1 о D(y)=(−∞; +∞). 2 о E(y)=[− 1; 1]. 3 о Функция нечетная. 4 о Если х = 0, то у = 0. π π о Функция возрастает при х [− 5 +2πn; +2πn]. 2 2 π 3π +2πn]. Функция убывает при х [ +2πn; 2 2 π π 6 о xmax = +2πn; xmin = − +2πn, где n Z. 2 2 Подробнее

Свойства функции y = cos x 1 о D(y)=(−∞; +∞). 2 о E(y)=[− 1; 1]. 3 о Функция четная. 4 о Если х = 0, то у = 1. 5 о Функция возрастает при х [−π+2πn; 2πn], n Z. Функция убывает при х [2πn; Π+2πn], где n Z. 6 o xmax = 2πn; xmin = π+2πn, где n Z. Подробнее

Свойства функции y = tg x π π (− +πn; +πn), где n Z. 2 2 2 о E(y)=(−∞; +∞). 1 о D(y)= 3 о Функция нечетная. 4 о Если х = 0, то у = 0. 5 о π π Функция возрастает при х (− +πn; +πn), 2 2 где n Z. 6 o Экстремумов нет. Подробнее

Свойства функции y = ctg x 1 о D(y)=(πn; π+πn), где n Z 2 о E(y)=(−∞; +∞). 3 о Функция нечетная. π х ≠ 0; у = 0 если х = +πn , где n Z. 2 5 о Функция убывает при х (πn; π+πn), где n Z. 4 о 6 o Экстремумов нет. Подробнее