 Ы Р К Е О Т В Выполнила: Ашимова Ильмира 1 АЭк
Ы Р К Е О Т В Выполнила: Ашимова Ильмира 1 АЭк
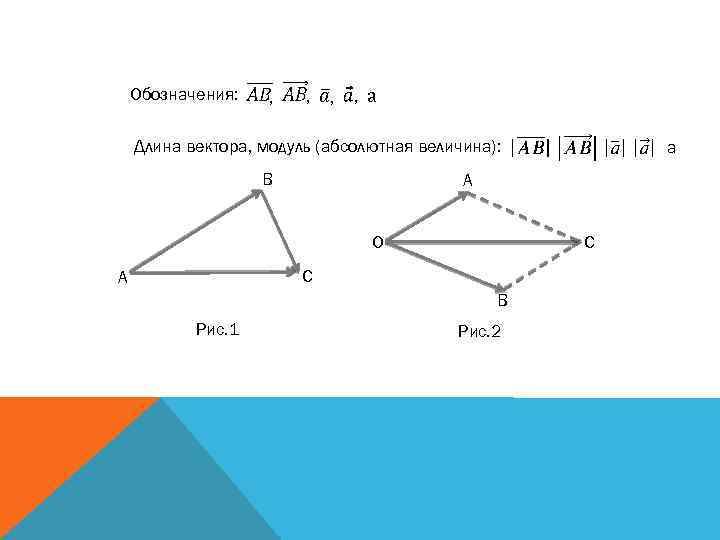 Обозначения: , , a Длина вектора, модуль (абсолютная величина): B A O C C A B Рис. 1 a Рис. 2
Обозначения: , , a Длина вектора, модуль (абсолютная величина): B A O C C A B Рис. 1 a Рис. 2
 СУММА ВЕКТОРОВ (правило треугольника) (рис. 1) (правило параллелограмма) (рис. 2) (правило многоугольника) (правило параллелепипеда, -диагональ)
СУММА ВЕКТОРОВ (правило треугольника) (рис. 1) (правило параллелограмма) (рис. 2) (правило многоугольника) (правило параллелепипеда, -диагональ)
 Разность векторов Формула вычитания векторов Признак коллинеарности векторов
Разность векторов Формула вычитания векторов Признак коллинеарности векторов
 ЗАКОНЫ ВЕКТОРНОЙ АЛГЕБРЫ Для любых векторов и любых чисел справедливы равенства
ЗАКОНЫ ВЕКТОРНОЙ АЛГЕБРЫ Для любых векторов и любых чисел справедливы равенства
 КООРДИНАТНЫЕ ФОРМУЛЫ Пусть - взаимно ортогональные единичные векторы, имеющие направления координатных осей; - координаты вектора или Если - начало вектора, - его конец, то
КООРДИНАТНЫЕ ФОРМУЛЫ Пусть - взаимно ортогональные единичные векторы, имеющие направления координатных осей; - координаты вектора или Если - начало вектора, - его конец, то
 Скалярное произведение векторов где - угол между векторами и и ; если : либо , то Из определения скалярного произведения следует, что где, например, есть величина проекции вектора Скалярный квадрат вектора: на направление вектора
Скалярное произведение векторов где - угол между векторами и и ; если : либо , то Из определения скалярного произведения следует, что где, например, есть величина проекции вектора Скалярный квадрат вектора: на направление вектора
 Свойства скалярного произведения: Векторное произведение векторов или - вектор, обозначаемый для которого: ( 1) - угол между векторами 2) 3) тройка и , , - правая. и , );
Свойства скалярного произведения: Векторное произведение векторов или - вектор, обозначаемый для которого: ( 1) - угол между векторами 2) 3) тройка и , , - правая. и , );
 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ Определение: Свойства смешанного произведения: - компланарны.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ Определение: Свойства смешанного произведения: - компланарны.
 ПРОЕКЦИИ ВЕКТОРА НА ОСЬ Обозначения: вектора на ось l. - проекции вектора Свойства проекций: на ось l; - величина проекции
ПРОЕКЦИИ ВЕКТОРА НА ОСЬ Обозначения: вектора на ось l. - проекции вектора Свойства проекций: на ось l; - величина проекции